Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

268

ГЛАВА 14

Как и в двумерном случае, элементарные объекты, определяемые функ-

цией (14.4), оказываются более удобными для представления и отображе-

ния полученных результатов, в то время как базисные объекты, определяе-

мые выражением (14.9), приводят к решению системы нормальных уравне-

ний, которые удачно разрешаются вычислительными средствами. Поясне-

ния будут приведены в следующем разделе.

Следуя рассуждениям разд. 6.3, будем предполагать, что имеется мно-

жество из / линейных непрерывных функций Щ вещественного переменно-

го,

которые отображают объект на вещественные числа. Обозначив через

R матрицу размером / х У, (/, У)-й элемент которой равен ^b

оконча-

тельно получим формулу вида

y = Rx + e (14.11)

[которая аналогична формуле (6.24)], в которой у

—

/-мерный вектор изме-

рений, /-я компонента которого равна измеренному значению .^/; х

—

J-

мерный вектор

изображения,

который необходимо найти при помощи со-

отношения (14.5) в виде оценки функции объекта /; е

—

/-мерный вектор

погрешностей. Таким образом, проблему вновь можно сформулировать в

следующем виде. Заданы данные у\ оценить вектор изображения х.

В реконструктивной томографии значения .^ обычно определяются сле-

дующим образом: предполагается существование / прямых линий, называе-

мых лучами и пронумерованных в пределах от

до /, которые соединяют в

трехмерном пространстве источник и приемник рентгеновского излучения.

Для произвольного объекта, описываемого функцией /, величина &f явля-

ется интегралом от f вдоль i-го луча. Приведенные в разд. 6.3 предположе-

ния о непрерывности не всегда выполняются при тех значениях /#,-, при ко-

торых они справедливы также и в данном случае.

Все ранее обсуждавшиеся методы решения системы уравнений (14.11) в

принципе можно использовать и в трехмерном случае, однако при этом ус-

ложняются проблемы, связанные с требуемым объемом вычислений, по-

скольку значения / и / приблизительно в 10 — 100 раз больше в трехмер-

ном случае, чем в двумерном. Во время написания данной книги имелось

лишь небольшое число работ, посвященных сравнению различных методов

разложений в ряды для реконструкции трехмерных изображений; поэтому

рассмотренный в следующем разделе один частный подход к этой пробле-

ме необходимо рассматривать лишь как пример реализации, а не как ре-

комендуемый алгоритм.

14.2.

РЕШЕНИЕ СИСТЕМЫ НОРМАЛЬНЫХ УРАВНЕНИЙ

ДЛЯ СПЕЦИАЛЬНОЙ ГЕОМЕТРИИ ТОМОГРАФИЧЕСКОЙ УСТА-

НОВКИ

Упомянутый выше частный подход состоит в минимизации нормы век-

тора ошибок по методу наименьших квадратов. Как показано в разд. 12.1,

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

269

наблюдаемый вектор изображения

удовлетворяет системе нормальных

уравнений вида/?

/?*

= R

Аналогично подходу, использованному нами

гл. 13,

здесь

мы

также попытаемся выбрать такое множество базисных

объектов

такую схему регистрации исходных данных, чтобы матрица

имела относительно простую структуру. Используя результаты разд.

13.1,

базисные объекты выбираем

соответствии

формулой (14.9),

схе-

му регистрации

—

такой, чтобы лучи

каждом ракурсе могли быть полу-

чены путем вращения лучей одного ракурса относительно некоторого цент-

ра.

Говоря более точно, предположим,

что

источник занимает

равноот-

стоящих друг

от

друга положений

(на

окружности радиусом

D в

плоскости

= 0) с

координатами

[£>, т(2ъ/М)

^г/2,

0] для m-го

положения

ис-

точника. Заметим, что данную схему можно реализовать

на

пятой модифи-

кации сканера (рис. 3.3,д) лишь при вращении сканера как целого вокруг

па-

циента.

Для

каждого

из М

положений источника имеется набор лучей,

вдоль которых будут зарегистрированы лучевые суммы.

Для

приведения

соответствие обозначений данной

предыдущих глав будем предполагать,

что

для

каждого положения источника имеется 27V

+ I

значений лучевых

сумм, пронумерованных

пределах

от

—А/

до N.

Предположим также,

что

при условии

—N < л ^ N

имеется

два

угла т

и о

п%

для

которых

при

< m < М

—

л-Й луч

от т-го

положения источника падает

под

углом

к плоскости

z = 0, а

проекция этого луча

на

плоскость

z = 0

составляет

угол

отрезком, соединяющим

т-е

положение источника

началом

ко-

ординат

(рис.

14.1).

Теперь можно записать положение произвольной точки

на л-м

луче

т-

го ракурса

цилиндрической системе координат

помощью параметра

пропорционального расстоянию вдоль луча.

точке

значение

принима-

ется равным нулю (рис. 14.1). Положение последней выбирается таким

об-

разом, чтобы линия, проведенная

из

начала координат перпендикулярно

проекции

л-го

луча

на

плоскость

z = 0,

пересекала проекцию

P в

точке

Я,

которая является проекцией точки

Q на ту же

плоскость. Если положить

= Ds\no„

(14.12)

0„,n,

= °

т(2п/М1 (14.13)

то видно,

что

точка

имеет цилиндрические координаты

/„, в

, 0, а

точ-

ка

Q —

координаты

(

, в

п т

, D cos о

tg о

Произвольная точка, отдален-

ная

на

расстояние

/ от

точки

Q в

направлении

имеет следующие коор-

динаты:

i\ftl + <

r cos т

»."i

Л'

cos

">'

D cos

°n

tan T

n -

sin т

(14.14)

ГЛАВА 14

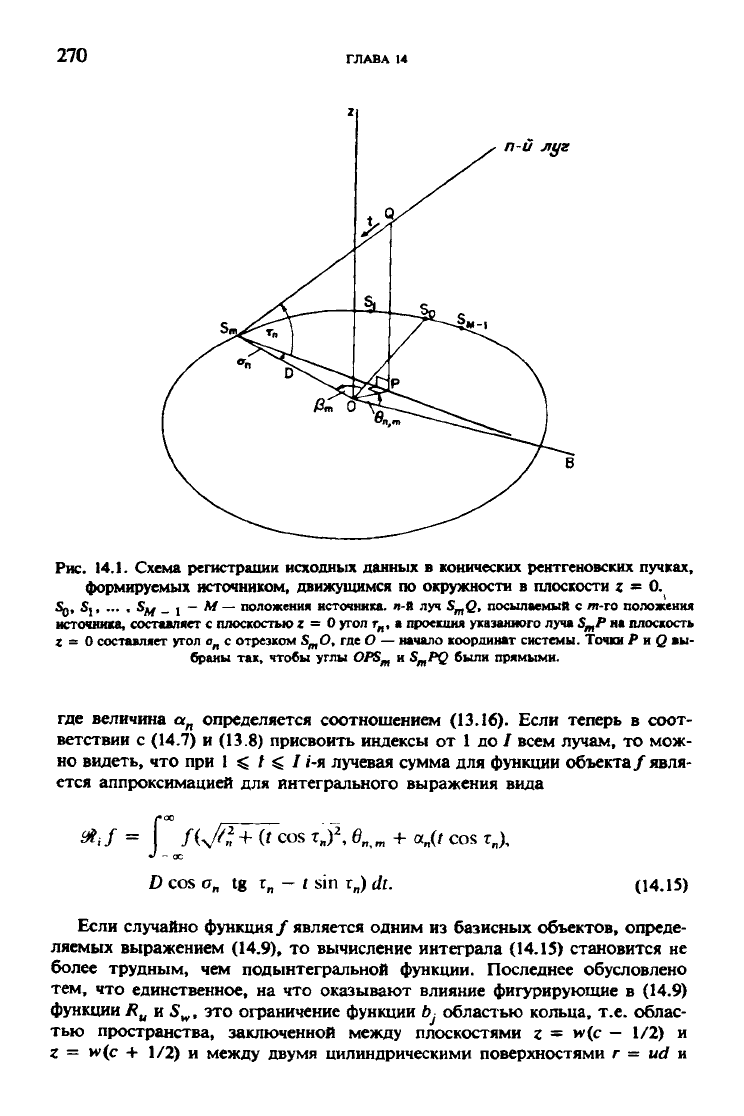
Рис. 14.1. Схема регистрации исходных данных в конических рентгеновских пучках,

формируемых источником, движущимся по окружности в плоскости z = 0.

SJj,

Sj, ... . S

_ | - M

—

положения источника, л-й луч S

Q, посылаемый с /я-го положения

источника, составляет с плоскостью z = 0 угол г„, а проекция указанного луча S

P на плоскость

г - 0 составляет угол о

с отрезком S

где О

—

начало координат системы. Точки Я и О вы-

браны так, чтобы углы OPS

и S

PQ были прямыми.

где величина а

определяется соотношением (13.16). Если теперь в соот-

ветствии с (14.7) и (13.8) присвоить индексы от 1 до / всем лучам, то мож-

но видеть, что при 1 ^ / < / /-я лучевая сумма для функции объекта/явля-

ется аппроксимацией для интегрального выражения вида

/•оо

&J = \ fiy/'l + (' cos т„)

, 0

+ а„(/ cos т

J - ОС

D cos o

tg r„ - t sin r

) dt. (14.15)

Если случайно функция / является одним из базисных объектов, опреде-

ляемых выражением (14.9), то вычисление интеграла (14.15) становится не

более трудным, чем подынтегральной функции. Последнее обусловлено

тем,

что единственное, на что оказывают влияние фигурирующие в (14.9)

функции R

и S

, это ограничение функции bj областью кольца, т.е. облас-

тью пространства, заключенной между плоскостями г = w (с

—

1/2) и

Z = iv (с + 1/2) и между двумя цилиндрическими поверхностями г = ud и

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

271

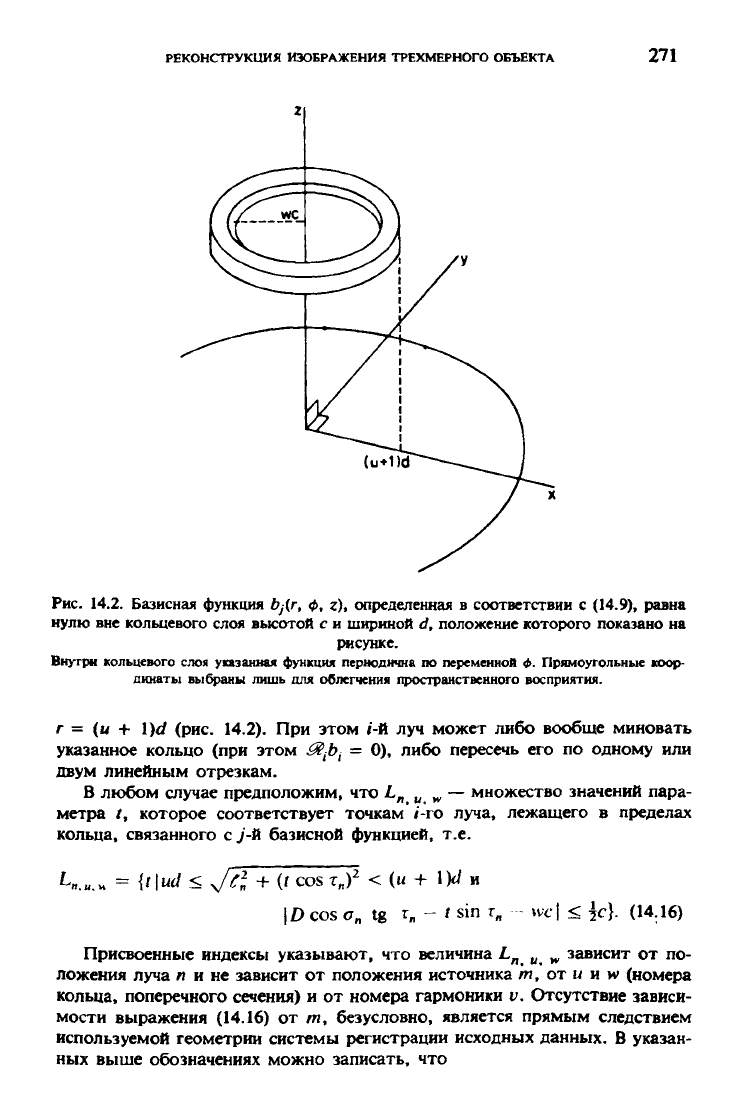
Рис. 14.2. Базисная функция bj{r, ф, г), определенная в соответствии с (14.9), равна

нулю вне кольцевого слоя высотой с и шириной d, положение которого показано на

рисунке.

Внутри кольцевого слоя указанная функция периодична по переменной

Ф.

Прямоугольные коор-

динаты выбраны лишь для облегчения пространственного восприятия.

г = (и + \)d (рис. 14.2). При этом i-й луч может либо вообще миновать

указанное кольцо (при этом ^

= 0), либо пересечь его по одному или

двум линейным отрезкам.

В любом случае предположим, что L

n и

— множество значений пара-

метра /, которое соответствует точкам /'-го луча, лежащего в пределах

кольца, связанного с

j-Pi

базисной функцией, т.е.

*-...,.* = {t\ud < У^

+ 0 cos т„)

< (и + 1W и

|D cos

<7„

tg г„ - I sin r„ vvel < ic}. (14.16)

Присвоенные индексы указывают, что величина L

n и w

зависит от по-

ложения луча п и не зависит от положения источника т, от и и и> (номера

кольца, поперечного сечения) и от номера гармоники v. Отсутствие зависи-

мости выражения (14.16) от т

безусловно, является прямым следствием

используемой геометрии системы регистрации исходных данных. В указан-

ных выше обозначениях можно записать, что

272

ГЛАВА 14

tfibj = Г

Т,{вп,т

+ «пС

COS

Г„)) dt, (14.17)

* 1*п

If. w

причем величина интеграла равна либо нулю (если множество

и w

пу-

стое),

либо значению интеграла с тем же подынтегральным выражением,

взятого по одному или двум связанным интервалам значений t.

Используя известные формулы для косинуса и синуса суммы двух аргу-

ментов, получим

nj = T

^Jn) + T^

(0„,

UtV

JnX (14.18)

где

cob(va

(t cos

TJ)

dt, (14.19)

(n) - Г sin(

11;

| a„(r

sin т

)) dt (14.20)

[ср.

с выражениями (13.21) и (13.22)].

Из приведенных выше соотношений следует, что элемент (R

)

мат-

рицы R'R в общем случае равен

= X С»

1р

,к»С„„„„

>)(1ТД,

)ТД,

))

и- -N \т = 0 /

+ I tf

.w>)G„

. „,.„>)( X Г,^^)^^^)

(14.21)

[формула (13.25)].

Напомнив теперь приведенную в разд. 13.1 теорему ортогональности, и

в частности соотношения (13.26) — (13.31), покажем, что еслиМ ^ IV + 1,

то справедливо равенство для

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА 273

«p.«;p.w

(w)W

.>v

(n)npH 1>

= г,,

UqtVqt%Vq

(n))

при

Ир

= -iv

О для остальных v

(14.22)

где определение величины h

дано после формулы (13.30). Последняя за-

пись означает, что матрица R

R имеет вид

P-V

®U(2W+l)

®L'12W+1) P-V+l

V(2W

Q-V+l

®1/<2W+1)

®U(2W+\) Qv-l Pv-1 ®V{2W+l)

Qv ®l/(2IF+l> ®V(2W

1) ^Y

(14.23)

где />„

(при условии что - V ^ v ^ И) являются матрицами размером

U(21V

+ 1) x U(2W + 1). Отметим, что матрица вида (14.23) не является

блочно-диагональной и, как это теперь установлено, не может быть инвер-

тирована так же просто, как в разд. 13.1. Рассмотрение вопроса о требуе-

мых корректировках будет отложено до обсуждения смысла каждой из

матриц

При условии, что

—

V ^ v < К, матрицу P

можно записать в виде

pi W+l, W) p(-IF+l, -IF+1)

/*IF.-W) piW.-W+l)

* v

p{-W+\,W)

*w.W)

(14.24)

где при -W < w' ^ W и -W < w" < W P^

™

т)

представляет собой

матрицу размером U х U, (Аг, / )-й элемент которой равен

(14.25)

274

ГЛАВА

В частности,

из

выражений (14.19)

(14.20) следует,

что P_

= P

при

- У

^ v ^ У.

Теперь рассмотрим определения

u v w

чИ

и v к

введенные выражени-

ями (14.19)

(14.20). Если m-Й

луч не

входит

в w-t

поперечное сечение

(т.е.

множество

L„

f w

при 0 < и < С/

—

является пустым),

то обе

величины

равны нулю. Если значения

w' и w"

таковы,

что

ника-

кой

из

лучей

не

пересекает

оба

поперечных сечения, обозначенные индекса-

ми

w' и w", то (/*"'•

=0при1^*^С/и1</^1/. Нетрудно

найти такие значения

w' HW";

очевидно,

что

если

w' >

и w" < 0, то ни

один

луч не

может пересечь

оба

сечения

(рис. 14.1 и

14.2).

В общем случае существует такое положительное целое число

(кото-

рое обычно меньше

что,

каково

бы ни

было значение

—

w" I > ft,

ие существует такого луча, который пересекал

бы оба

поперечных сечеиия,

обозначенных индексами

w' и w".

Здесь

ранее подразумевалось,

что

• *о

при

> П.

(14.26)

Матрицу рассмотренного выше вида будем называть блочно-

полидиагональной. Хотя обращение блочно-полидиагональной матрицы

выполнить

ие так

просто,

как в

случае блочно-диагональной,

тем не

менее

существуют алгоритмы обращения блочно-полидиагональных матриц,

бо-

лее быстрые,

чем

универсальные алгоритмы обращения.

Рассмотрим теперь матрицу

(14.23).

При

условии

что

—

^ v ^ К,

матрицу

можно записать

виде

бг

W) Q

{

-W,-W+l)

QC-W-H,

Qi-W+l,-W+l)

•

{

W4tl ,W)

\W,~W)

MW.-w+i)

\lW.W)

(14.27)

где

при

—

W ^ w' ^ IV н IV ^ w" ^ W она

представляет собой матрицу

размером

U х (У, (k

i )-й

элемент которой равен

«2\Г

'%n= у I

(H*-i.,.Uw)G/-i.„.

-(w)

n= -N

+ С*-1..;.|Дл)Я/-1.|;,.Ли)).

(14.28)

Заметим,

что из

выражений (14.19)

(14.20) следует равенство

G-!,

= Q

при - У < v < ^, а

также равенство

= 6

Исходя

из

соображений, аналогичных приведенным после формулы

(14.25),

можно показать,

что

матрица

также является полидиагональ-

иой.

В заключение отметим,

что

перестановкой элементов строк

столбцов

матрицы (14.23)

[что

эквивалентно использованию иной схемы индексации

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

275

в матрице (14.8)] можно привести данную матрицу к блочио-

диагональному виду с У + 1 блоками, один из которых (а именно блок Р

)

имеет размер U(2W + 1), а остальные (а именно различные комбинации

блоков P

, P_

, Q

и Q_

) — размер 21/(2 W + 1). Кроме того, каждый из

расположенных на диагонали блоков можно представить в блочно-

полидиагональной матрице. Таким образом, можно получить решение си-

стемы нормальных уравнений, связанной с решением проблемы рекон-

струкции изображений полного трехмерного объекта.

Подводя итоги сказанному, отметим, что путем соответствующей ин-

дексации базисных объектов, до некоторой степени отличающейся от ис-

пользованной в выражении (14.8), матрица R

R в нормальной системе

уравнений становится блочно-диагональной с блоками Р

, /?,, . . ., R

Блок Р

представляет собой блочно-полидиагональную матрицу в форме

(14.24),

состоящую из блоков /$*'•

"\ определяемых согласно выражению

(14.25).

Блоки R

(при 1 ^ v ^ У) также являются блочно-

полидиагональными матрицами вида

ftiW.-W)

n(W. W + \)

IUW.W)

При -W < w* < W и -W < w" ^ W имеем

(14.29)

v \dv I

(14.30)

где величины P<"'

и £<*"'• "'* определены выражениями (14.25) и (14.28)

соответственно.

В частности, если

w' - w" I > П, то

'»

> — нулевая матрица 0

2(/

[условие (14.26)].

14.3.

ПОСТРОЕНИЕ ДИНАМИЧЕСКИ ИЗМЕНЯЮЩИХСЯ

ТРЕХМЕРНЫХ ФАНТОМОВ И ИХ ПРОЕКЦИЙ

При опробовании различных алгоритмов реконструкции, необходимых

для четырехмерной (пространственно-временнбй) информации, мы сталки-

ваемся с проблемой создания подходящих фантомов органов и проекцион-

ных данных. Подобная же проблема существовала и в двумерном случае; &

данном разделе мы рассмотрим и проиллюстрируем четырехмерный вари-

ант решения упомянутой проблемы. Здесь мы ограничимся рассмотрением

конкретного устройства, хотя имеется и целый ряд других возможных при-

ложений метода.

276

ГЛАВА

Рис. 14.3. Макет динамического пространственного реконструктора (ДПР).

В верхней части рисунка видиа система

из 28

рентгеновских трубок

расположенным напротив

полуцилиндричсскнм флуоресцентным экраном,

которым связана система

из 28

видеокамер,

на-

ходящаяся

нижней части круговой рамы. (Снимок предоставлен д-ром

Е. Л.

Рит мал ом.)

Динамический пространственный реконструктор (ДПР) представляет

собой устройство, построенное в Отделе биодинамических исследований в

клинике Майо для неинвазивной визуализации работающего сердца в не-

поврежденной грудной клетке, а также для других задач. Устройство со-

стоит из 28 источников рентгеновского излучения, расположенных на дуге

окружности с интервалом по углу 6° и согласованных с 28 системами ото-

бражения. Грудная клетка пациента целиком проецируется на двумерный

экран системы отображения с помощью конических пучков рентгеновского

излучения от источников, включающихся и выключающихся на время 10 мс

с частотой 60 Гц. Система непрерывно вращается, совершая полный обо-

рот за 4 с (т.е. приблизительно за четыре цикла сокращений сердца). За это

время каждый рентгеновский источник последовательно занимает все 240

положений. Фотография модели ДПР приведена на рис. 14.3.

Для опробования используемых в ДПР алгоритмов необходимо преду-

смотреть возможность получения исходных данных того же типа, что и

получаемые в ДПР на объектах известной формы. Программное обеспече-

ние ЭВМ для ДПР разрабатывалось для описания динамически изменяю-

щихся трехмерных объектов и последующего моделирования процесса по-

лучения в ДПР рентгеновских проекций.

Фантомы в программах ДПР вводились в виде набора эллипсоидов,

каждый из которых определялся десятью параметрами, три из которых да-

ют положение в пространстве центра эллипсоида, три другие дают значе-

ния длин его осей, еще три характеризуют ориентацию эллипсоида в про-

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

277

шсгеглЮВистхиик1

таетэисткнмт

\fmczew5licmozHUK27

ткгетШтогникгв

Шсгетгистоеник2\

ч)тштбистогник1

шпсгет Шстогшг

wnaemSUcmoamf

Мстогникп

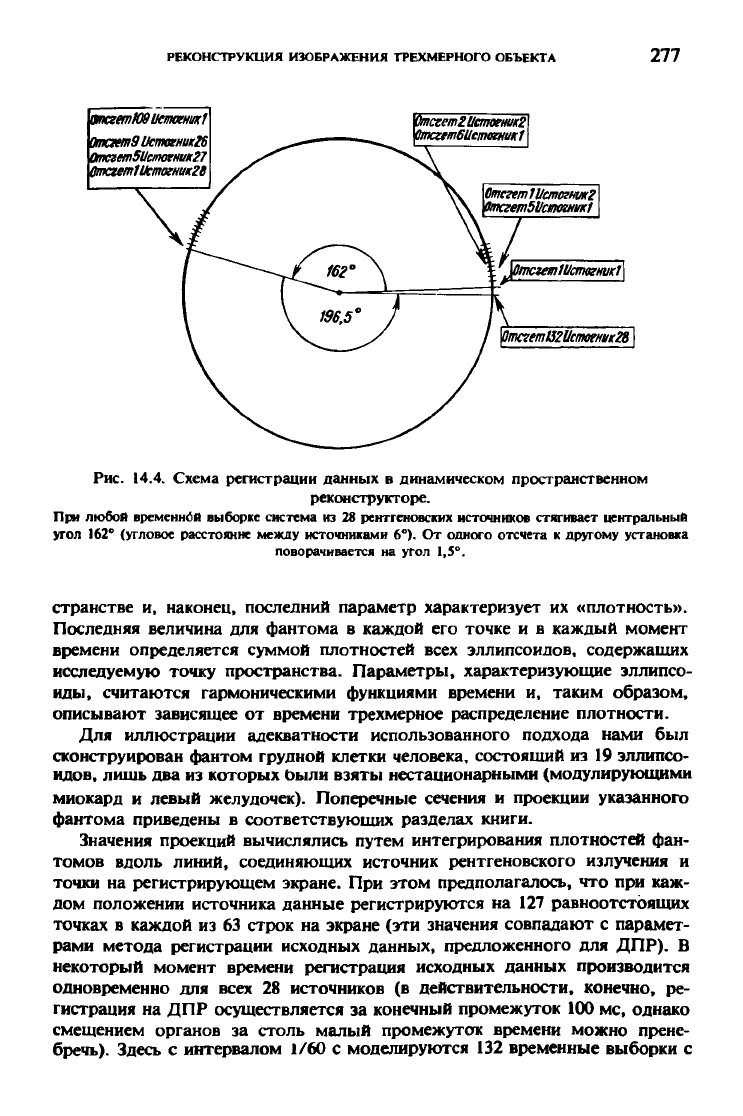
Рис.

14.4. Схема регистрации данных

динамическом пространственном

реконструкторе.

При любой временной выборке система из 28 рентгеновских источников стягивает центральный

угол 162° (угловое расстояние между источниками 6°). От одного отсчета к другому установка

поворачивается на угол 1,5°.

странстве

и,

наконец, последний параметр характеризует

их

«плотность».

Последняя величина

для

фантома

каждой

его

точке

и в

каждый момент

времени определяется суммой плотностей всех эллипсоидов, содержащих

исследуемую точку пространства. Параметры, характеризующие эллипсо-

иды,

считаются гармоническими функциями времени

и,

таким образом,

описывают зависящее

от

времени трехмерное распределение плотности.

Для иллюстрации адекватности использованного подхода нами

был

сконструирован фантом грудной клетки человека, состоящий

из 19

эллипсо-

идов,

лишь два

из

которых Ьыли взяты нестационарными (модулирующими

миокард

левый желудочек). Поперечные сечения

проекции указанного

фантома приведены

соответствующих разделах книги.

Значения проекций вычислялись путем интегрирования плотностей фан-

томов вдоль линий, соединяющих источник рентгеновского излучения

точки

на

регистрирующем экране.

При

этом предполагалось,

что при

каж-

дом положении источника данные регистрируются

на 127

равноотстоящих

точках

каждой

из 63

строк

на

экране (эти значения совпадают

парамет-

рами метода регистрации исходных данных, предложенного

для

ДПР).

некоторый момент времени регистрация исходных данных производится

одновременно

для

всех

источников

(в

действительности, конечно,

ре-

гистрация

на ДПР

осуществляется

за

конечный промежуток 100 мс, однако

смещением органов

за

столь малый промежуток времени можно прене-

бречь).

Здесь

интервалом

1/60 с

моделируются

132

временные выборки