Heinrich J.G., Aldinger F. (Eds.) Ceramic Materials and Components for Engines

Munz

and Fett [6] also reported a modification of

equs. 1-3 for a finite loading length

a.

The stress

distribution in the disc along the y-axis (x

=

0)

is:

In fig. 2 the ratio, R,

,

of the amplitudes of the

maximum compressive stress components in the loading

area to the maximum tensile stress components in the

centre of the specimen is plotted against the ratio of the

half contact length

a

to the disc diameter

R.

loo,

I

Fig. 2: Ratio of the amplitudes of the max. compressive

stress at the support area to the max. tensile stress in

the centre

of

the disc as a function of a/R.

Fig. 3: Valid failure mode (left) gained on the modified

BDT and invalid failure (right) gained

on

flat support on

electro-ceramic samples.

A

small contact length as it is the case for ceramic

materials on a hardened steel jig the maximum

compressive stress amplitude is much higher than the

maximum tensile stress. Therefore, a different failure

mode caused by these compressive stresses is often

observed, (triple cleft failure) as shown

in

fig. 3 right.

This happens also when testing advanced ceramics even

if these materials have a much higher compressive then

tensile strength. FE calculations have shown that

compressive stresses can be up to 30 times higher than

the tensile stresses [5]. Experiments on electro-ceramic

samples show that nearly

100%

of the samples fail

in

the triple cleft failure mode leading to invalid

experiments.

It was also observed that these large compressive

stresses lead to crack initiation in the support (a

hardened steel support) at the contact area (Hertzian

contact cracks). To be able to use this testing method for

advanced ceramics a modification of the support

geometry in order to increase the contact area and to

decrease the compressive stresses has been carried out.

FE calculations were done to determine an

advantageous curvature

of

the support.

NUMERICAL SOLUTION

To study the effect of curvature of the support and

of different support and test specimen materials a

parametric FE study has been carried out using a 2D and

a 3D contact mechanical model. The software used was

ANSYS

(Vers. 5.5). In the first approach a 2D model of

a quarter

of

the test assembly has been modelled. To test

the accuracy of the model in a first step a flat support

was verified by comparison with the standard analytical

solutions (fig. 4.a). In a second step the influence of a

curved support on the stress distribution was evaluated

using the curvature as a modelling parameter (fig.

4.b).

Fig.

4:

Quarter 2D-model of the brazilian disc test with

a) planar and b) curved support (the support radius is

here 5% bigger than the disc radius).

The results of the 2D model of the flat support

show very good agreement with those of the analytical

solution. The stress distribution along the x and y-axis

fits nearly perfectly along the hole diameter of the disc.

Only near the contact point between disc and support a

small deviation of the compressive stresses achieved in

the FE solution and in the analytical solution was

observed. Also the stress distribution in the support was

determined, showing large tensile stresses in the surface

next to the contact area. This is exactly the area where

212

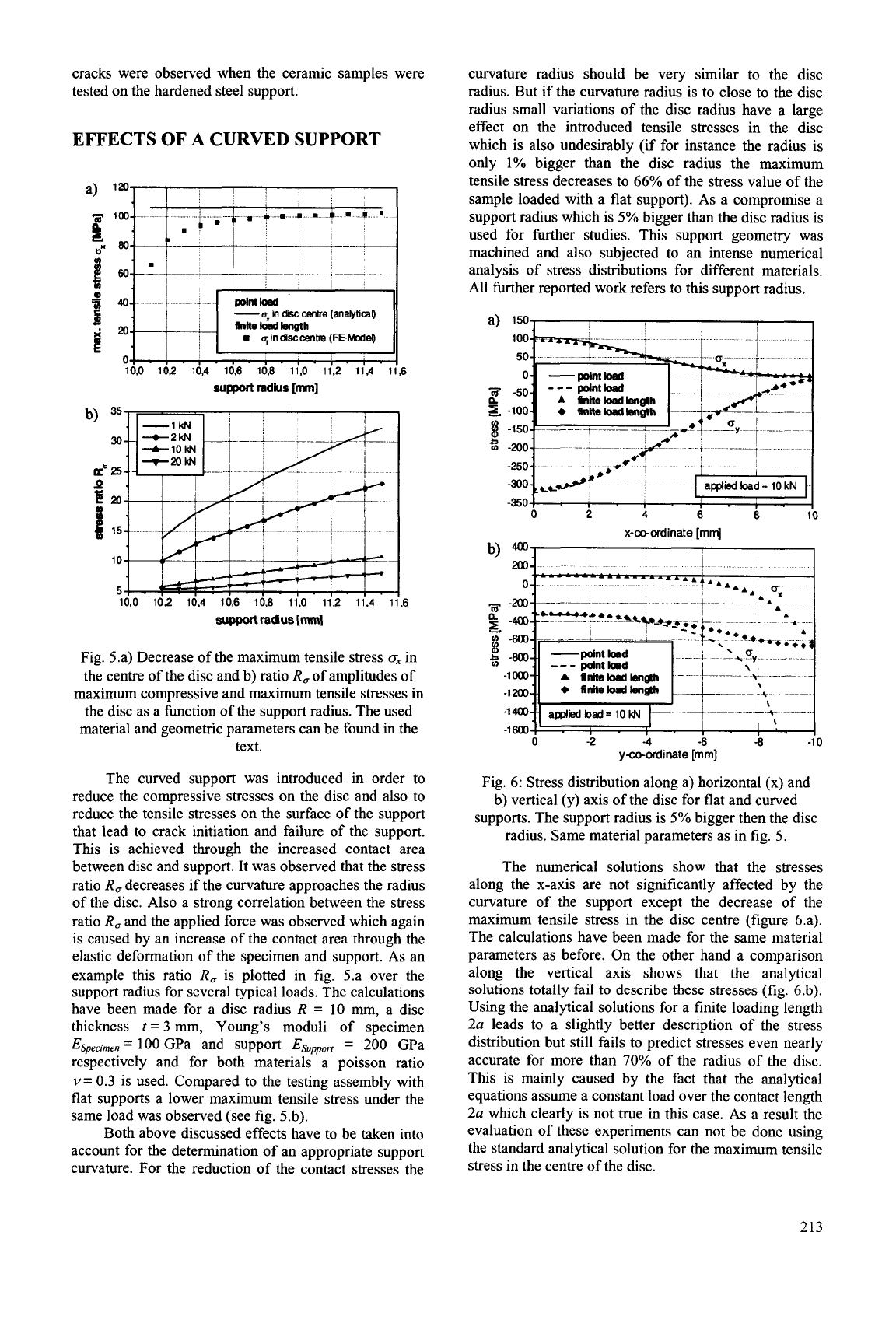
cracks were observed when the ceramic samples were

tested on the hardened steel support.

EFFECTS OF

A

CURVED SUPPORT

l

r

00

10.0 102 10,4 10.6 108

11,O

11.2 11.4 11.6

support

radius

[mn]

+lo

161

-20161

10,O

10.2 10.4 10,6 10.8

11,O

11.2 11.4 11.6

support

radus

[mm]

Fig. 5.a) Decrease of the maximum tensile stress

o,

in

the centre of the disc and b) ratio

R,

of amplitudes of

maximum compressive and maximum tensile stresses in

the disc as a function of the support radius. The used

material and geometric parameters can be found in the

text.

The curved support was introduced in order to

reduce the compressive stresses on the disc and also to

reduce the tensile stresses on the surface of the support

that lead to crack initiation and failure of the support.

This is achieved through the increased contact area

between disc and support. It was observed that the stress

ratio

R,

decreases if the curvature approaches the radius

of the disc. Also a strong correlation between the stress

ratio

R,

and the applied force was observed which again

is caused by an increase of the contact area through the

elastic deformation of the specimen and support. As an

example this ratio

R,

is plotted in fig. 5.a over the

support

radius for several typical loads. The calculations

have been made for a disc radius

R

=

10

mm,

a disc

thickness

t

=

3

mm,

Young's moduli of specimen

Especimr,,=

100

GPa and support

Esupporf

=

200

GPa

respectively and for both materials a Poisson ratio

v=

0.3

is used. Compared to the testing assembly with

flat supports a lower maximum tensile stress under the

same load was observed (see fig. 5.b).

Both above discussed effects have to be taken into

account for the determination of an appropriate support

curvature. For the reduction of the contact stresses the

curvature radius should be very similar to the disc

radius. But if the curvature radius is to close to the disc

radius small variations of the disc radius have a large

effect on the introduced tensile stresses in the disc

which is also undesirably (if for instance the radius is

only

1%

bigger than the disc radius the maximum

tensile stress decreases to

66%

of the stress value of the

sample loaded with a flat support). As a compromise a

support radius which is 5% bigger than the disc radius is

used for further studies. This support geometry was

machined and also subjected to an intense numerical

analysis of stress distributions for different materials.

All hrther reported work refers to this support radius.

a)

150,

I

-250-

t

-350,.

,

.

;

.

i

.

I.

I

-300:

LcLedc

*,

applied

bad

=

10

kN

0

2

4

6

8

10

x--ordinate

[mm]

I

1

b)

4001

200-

0-

---A;;--

..-..AA

A~**

-12001~

+

finitekadlengh

d+.-

I'

-1400:-

adled

bad=

10

IQ\1

1----1

--

It

-

.

-I

6a)

I

.

1'.

0

-2

-4

-6

-8

-1

0

yco-ordinate

[mm]

Fig.

6:

Stress distribution along a) horizontal (x) and

b) vertical (y) axis of the disc for flat and curved

supports. The support radius is

5%

bigger then the disc

radius. Same material parameters as in fig.

5.

The numerical solutions show that the stresses

along the x-axis are not significantly affected by the

curvature of the support except the decrease of the

maximum tensile stress in the disc centre (figure 6.a).

The calculations have been made for the same material

parameters as before. On the other hand a comparison

along the vertical axis shows that the analytical

solutions totally fail

to

describe these stresses (fig. 6.b).

Using the analytical solutions for a finite loading length

2a leads to a slightly better description of the stress

distribution but still fails to predict stresses even nearly

accurate for more than

70%

of the radius of the disc.

This is mainly caused by the fact that the analytical

equations assume a constant load over the contact length

2a

which clearly is not true in this case. As a result the

evaluation of these experiments can not be done using

the standard analytical solution for the maximum tensile

stress in the centre of the disc.

213

Fig. 7: Stress distribution in the disc

(R

=

10 mm)

a) and b)

on

a flat and c) on a curved support (support

radius

5%

bigger than the disc radius). Plotted are

q,

ox,

and

q,

respectively. Same parameters

as

before.

112

1

Fig. 7 shows results of some of the performed FE-

calculations.

In

figs. 7.a and b the flat support situation

is modelled, showing the first principal stresses,

oI,

and

the stress

ox,

respectively. Fig 7.c shows the first

principle stresses,

q,

on

a curved support. The curved

support leads to a decrease of the maximum tensile

stress in the centre of the disc and also to a decrease of

the volume fraction that is under tensile stresses. This

1

-4.953.104-q

+2.173.107.ax2

1

-

5.890-104.~, +2.699.10-’0,~

has some influence

on

the effective loaded volume

of

the specimen.

EVALUATION

OF

THE

MAXIMUM

TENSILE

STRESS

IN THE DISC

As already mentioned the maximum tensile stress

in the centre

of

the disc is influenced by the

experimental conditions. It can be expressed by

modifying equ.

5

with a correction factor

C:

which depends

on

the elastic properties of the testing

and support materials, the radii of support and specimen

and the applied load. It is plotted over the applied load

in fig. 8.a for a disc radius of

R

=

10

mm. The support

curvature is the parameter. The same material

parameters

as

in the previous figures are used. It is

obvious that the factor

C

reaches one if the support

radius approaches infinite (flat support). With

increasing applied load,

F,

the elastic deformation of

specimen and support and also the contact area increase,

causing a decrease of the maximum tensile stress in the

disc centre compared to the flat support situation.

In

principle the factor

C

has to be evaluated for every

geometry, for every material combination and every

applied load. In Fig. 8.b the factor

C

is plotted over the

maximum tensile stress in the specimen (defined by

equ.10). Shown are results for several different

specimen radii and ratios of the elastic moduli of testing

and support material. For both materials the Poisson

ratio is assumed to be 0.3. It can be seen that for a

constant ratio of moduli the result does not depend

on

the disc radius. Analytical fit equations for the factor

C

for

three different ratios of moduli are given

in

Tab.

1.

The stress

a,

is given by equ. 10. These equations have

to be solved iteratively.

Table.

1

:

Approximate equations for

C

for different

combinations of Youngs moduli of specimen and

support materials for a support radius

5%

bigger than

the disc radius.

I

EstIec1men

1

ESuLlDort

I

C

I

312

I

1

-4.954.10~4.~+2.174~10-7~,2

I

A

3D

model of the test assembly shows

no

significant changes

on

the stress distribution except a

negligible decrease of the tensile stresses near top and

base surface of the disc.

EXPERIMENTAL INVESTIGATIONS

For the fracture experiments disc shaped electro-

ceramic samples

(E

=

100

GPa,

v=

0.3) were used. The

samples were tested

in

the as sintered condition with a

diameter of

20

mm

(+O,O

1

mm

I

-0,02 mm) and a height

of

3,26

mm

(k

0,059). Using the standard BDT support

214

geometry only ten samples were tested. All these maximum tensile stress in the sample which is right

samples showed triple cleft failure, fig.

3

(right).

Also

below the loading point. Fractography proves that

the support showed significant cracks on the surface fracture starts

-

as in the case of bending specimens

-

at

near the contact area between the specimen and the

internal defects (pores).

support. Therefore all further tests were performed with

the modified testing assembly. All

30 tested samples

showed the tensile failure mode as seen in fig. 3 (left).

As a reference testing method a miniaturised 4-point

bending testing method described in

[7]

was used. For

these tests mini-bending bars

(30

specimens) with a

geometry 1,5x2x15 mm were machined from the discs.

Table.

2:

Results of the strength tests. The description

can be found in the text.

confid. int. (103

-

108) (107- 111)

ax

in

the

centre

of

the

disc

[MPa]

Fig. 8:Correction factor C a) over the applied load for a

disc with radius

R

=

10

mm and for several different

support radii and b) over the max. tensile stress

0;

for

specimens with different radii and different ratios of

Young's moduli of tested material to support material.

The support radius is

5%

bigger than the disc radius.

The test results are reported in table

2.

For the

BDT tests the maximum principal stress (in ceramics

tensile failure is in general triggered by this stress

component

[6,

81)

and for the bending tests the

maximum outer fibre stress are given respectively. For

each data set the characteristic strength, its

95

%

confidence intervall, the Weibull modulus and its 95

%

confidence interval1 are given (data evaluation with

Weibull theory is common practice when testing

ceramics

[6,

8,

91). Within the scatter of the data no

significant difference between the strength data can be

observed.

A

comment on the need to apply Weibull

theory in order to describe the Brazilian Disc testing of

ceramic materials is given in the appendix.

Fig. 9 shows a macroscopic image of the fracture

surface of a BDT sample tested on a curved support.

Fracture clearly starts from within the area of the

confid. int.

1

(11

-

19) (15-24)

1

crack origin

Fig.

9:

Macroimage

of

a typical BDT fracture surface of

a specimen tested using the modified support.

CONCLUSIONS

Brazilian disc testing with a flat support can result

in undesired failure starting from the loading point,

especially if testing high strength materials.

0

A

new design of the support reduces the

compressive stresses in the support area and provokes

specimen failure from the tensile loaded disc centre.

In the newly designed jig the tensile stresses in the

centre of the specimen are smaller than in the standard

configuration if tests are performed at the same load.

The reduction depends on geometrical conditions of

the support, the applied load and the ratio of the

Youngs moduli of specimen material and support

material, respectively.

For a support with a curvature

5%

bigger than the

specimen radius for a wide range of possible material

parameters the tensile stresses have been calculated.

0

Tests performed on an electro-ceramic

(bariumtitanate) material give the same strength

values when tested in 4-point bending and in the

Brazilian disc test configuration.

0

APPENDIX:

THE

EFFECTIVE VOLUME

The fracture probability of ceramics is commonly

described by the Weibull distribution function,

F(o,.),

which for a homogenous tensile loading is

[6,

91:

with

oi,

and m as parameters of the distribution.

V,

is a

scaling volume. The Weibull hnction predicts a

dependence

of

the probability of failure on the the

215

loaded Volume

V.

This is a consequence of brittle

failure from sparsly distributed flaws [9, 101 (it is more

likely to find large flaws in large than in small

volumes).

In order to take into account for a inhomogenous

and multiaxiale stress state, a suitable multiaxial failure

criterion (resulting in an equivalent stress,

oe)

and the

effectively loaded volume have to be defined (for details

see [6, 81 and the literature therein). In the following the

maximum principle stress is used in place of the

equivalent stress and the effective volume is given by:

Using a method for numerical integration, the

so

called Gaussian quadratur

[

1 11, the effective volume can

be calculated from the FE model. Fig. 10 shows the

relationship between the effective volume and the

Weibull modulus for the point loading case, an older

analytical approximation found in the literature

[

121 (it

describes also the point loading case) and the used

modified BDT configuration. Of course the effective

volume goes to zero if the Weibull modulus goes to

infinity (indicating no data scatter; then the fracture

origin must start in the maximale loaded volume

element). The reduction of the effective volume in the

tests made with a curved support compared with the

point loading case reflects the fact that the tensile

loaded volume is significantly reduced if a sample is

loaded on curved supports.

This

can qualitatively also

be seen by comparison of Figs.7.a and 7.c.

poln

load:

-=rvtical(Neergaard)

-flatSuppott(FE)

Wruppoct

-

R=10,5mm

I

s

5%

I

>

.-

modul

m

Fig. 10: Ratio of the effective volume Vcfand of the

disc volume as a function of the Weibull modulus.

Shown are different approximations.

In general (as shown e.g. for some structural ceramics

[6, 7, 8, 13, 141) a proper comparison of BDT- and

bending test data necessitates to take into account for

the different effective volumes in both kinds of testing

(the effective volume in BD testing is about ten times

higher than that of the mini bending samples; a Weibull

extrapolation of strength for m=17 and V,lV2=10 would

result in an 15% increase in the bending strength). But

for the investigated material no influence of volume

under load on strength has been observed within the

experimental scatter

[

13, 141 and the comparison of data

as made in table 2 seems to be fair. This behaviour is

yet not fully understood and still matter of

investigations.

ACKNOWLEDGEMENTS

The authors thank EPCOS AG/Deutschlandsberg

(Austria) for supplying samples, and acknowledge the

collaboration of I. Hahn (SIEMENSMunich), J. Riedler

and G. Schoner (EPCOS) for providing some of the

requested material data and the helpful discussions on

related topics. This work was supported by the Austrian

Kplus-program.

REFERENCES

(1) B. W. Darvell, Uniaxial compression tests and the

validity of indirect tensile strength, J. Mat. Sci., 25,

(2) A. Briickner-Foit, T. Fett,

D.

Mum, Discrimination

of Multiaxiality Criteria with the Brazilian Disc

Test, J. Eur. Cer. SOC., 17, (1997) 689

-

696

(3) R.H. Marion, K.J. Johnstone, A Parametric Study

of the Diametral Compression Test for Ceramics,

Cer. Bull., 56, (1977) 998

-

1002

(4) U. Soltesz,

G.

Bernauer, R. Schafer,

Spaltzugversuchs-Eignung

zur Zugfestigkeits-

Ermittlung sprodbrechender Materialien,

Fachberichte DKG, 72, (1995) 553

-

555

druckversuches fur keramische Materialien,

Diplomarbeit an der Montanuniversitat Leoben,

Austria,

(

1999)

(6) D. Munz, T. Fett, Ceramics Mechanical Properties,

Failure Behaviour, Materials Selection; Springer

Verlag, Berlin, Germany, (1999)

(7) T. Lube, M. Manner, R, Danzer, The

Miniaturisation of the 4-point bend Test. J. Fatigue

Fract. Engng. Mater. Struct., 20, (1 997) 1605- 16 16

(8) D. Rubesa, R. Darner; The Pecularities of

Designing with Brittle Materials-Weak Point and

Deficiencies, Proc. of the 12'h Bienniel Conference

on Fracture

-

ECF 12, EMAS Publishing, West

Midlands, Sheffield,

U.K,

(1

998)

(9) R. Darner; Ceramics: Mechanical Performance and

Lifetime Prediction; Encyclopedia of Advanced

Materials;

1,

Oxford, (1994) 358-398

(10)R. Darner, A general strength distribution function

for brittle materials.

J.

Eur. Ceram. SOC. 10, (1992)

(1 l)A.

H.

Stroud and D. Secrest, Gaussian Quadrature

(1990) 757-780

(5) A. Borger, Optimierung des Scheiben-

46 1-472

Formulas, Prentice-Hall, Inc.. Englewood Cliffs.

N. J.,USA,

(1

969)

diametral compression, J. Mat. Sci., 3, (1997) 2529

(12)L.J. Neergaard; Effective volume of specimens in

-

2533

(13)R. Danzer, T. Lube, Fracture statistics of brittle

materials: It does not always have to be Weibull

statistics. Proc.

6'h

Int Symp. Ceramic materials and

components, Arita, Japan,

(

1998) 658-662

(14) R. Danzer, Mechanical behaviour and reliability of

Ceramics. in. P. Vincencini ed. gth Cimtec-World

Ceramics Congress, Faenza, Italy, (1999) 379-386

216

THE IMPULSE EXCITATION TECHNIQUE FOR RAPID ASSESSMENT OF

THE TEMPERATURE DEPENDENCE OF STRUCTURAL PROPERTIES OF

SILICON NITRIDE AND ZIRCONIUM OXIDE CERAMICS

G.

Roebben*,

R

G.

Duan, B. Basu,

J.

Vleugels,

0.

Van der Biest

Department of Metallurgy and Materials Engineering,

Katholieke Universiteit Leuven, de Croylaan

2,

B-3001 Heverlee, Belgium

ABSTRACT

This paper presents the Impulse

Excitation Technique (IET) as a means of

non-destructive high temperature mechanical

testing. IET enables to determine both elastic

and damping or internal friction properties

of

small laboratory samples

as

well

as

industrial

components. As an example, the changes with

temperature of stiffness and internal friction

of silicon nitride engine valves will be shown,

and their impact on the valve performance

will be discussed. Further the effect of

temperature on the internal friction

of

small

test samples

of

different grades of silicon

nitride as well

as

zirconia ceramics (Y-TZP

type) is reported.

INTRODUCTION: THE IMPULSE

EXCITATION TECHNIQUE (IET)

Careful characterisation of the

mechanical properties of ceramic materials

and components is required before structural

application can be attempted. However, often

the amount of test-material

-

in laboratory-

scale processing

-

or test-time

-

in the field of

industrial production

-

is restricted. This can

prohibit large-scale strength statistics and

creep exercises. Also, the latter tests are

destructive,

and

unsuitable for quality control.

Alternatively, a considerable amount of

structural information can be obtained from

small laboratory samples

as

well

as

finished

components, in a rapid and non-destructive

manner, using the Impulse Excitation

Technique (IET).

IET is a particular type of resonance

frequency analysis. It essentially consists

of

inducing the vibration of a freely suspended

test sample by a gentle, non-destructive

mechanical impulse. Forster described the

principal test procedure as early as 1937 [l].

Developments in digital signal analysis

allowed substantial progress in the IET-

domain in the last few years [2]. The results

obtained by IET consist of the resonance

frequencies of the tested sample, and the rate

at which each of these frequencies loose

amplitude with time after the impulse

excitation. The resonance frequencies are

related to the sample’s stiffness, whereas the

(exponential) amplitude decrease reflects

material damping or internal fiction [3].

IET,

as

well

as

other resonance

frequency tests, have been widely

acknowledged

as

an economically viable and

sensitive means of product quality control

[4,5]. Moreover, the non-destructive character

of

IET implies that a single sample can be

tested periodically, e.g. during a temperature

cycle.

In

this paper, it is shown how IET

provides access to changes in stiffness and

internal friction with temperature. These

observations can be related to otherwise less

easily accessible properties as fracture

toughness and creep resistance.

EXPERIMENTAL

Impulse excitation equipment

Impulse excitation tests were performed

with a Resonance Frequency and Damping

Analyser apparatus (RFDA, Integrated

Material Control Engineering (IMCE),

Diepenbeek, Belgium), which has been

217

Figure

I

a) Set-up for tests

in

air constructed

on

the frontflange (5) of the furnace chamber, before insertion

in

the chamber. The rectangular test sample

(I)

is suspended with NiCr-wires

(2)

that are guided along

freely turning ceramic cylinders

(3)

between parallel

A1203

rods. Two of the

A1203

rods are driven by a step-

motor to prevent change of sample position by thermal expansion and creep of the wires; b) Graphite

sample suspension platform

(5)

equiped with a shielded thermocouple

(2),

a tube

(3)

through which a

ceramic projectile is fired, with a ceramic engine valve

(I)

suspended by graphite threads

(4),

ready for

insertion

in

bottom-loaded graphite-heating-element furnace.

previously described in [2]. Tests were

performed both in a fi-ont-loaded air-hace

(Fig. 1 a, J.

W.

Lemmens, Leuven, Belgium),

and in a bottom-loaded graphite fiunace (Fig.

1 b, HTVP-l75O-C, IMCE, Diepenbeek,

Belgium).

An

automated impulse excitation

method is used, consisting of an either

pneumatically (air furnace) or electro-

magnetically (graphite furnace) fired ceramic

projectile. The sample vibration is detected

-

by default

-

with a microphone. Laser

vibrometry provides an alternative for

challenging atmospheres (vacuum) or samples

(lightweight). The RFDA software analyses

the digitally stored vibration signal. After

an

initial Fast Fourier Transformation, the

program uses an iterative algorithm to

simulate the time-domain sound signal, thus

determining the main frequencies present in

the recorded vibration,

as

well

as

the

exponential loss factor corresponding to each

of the detected frequencies. This loss factor

indicates how fast the amplitude of the

vibration component of that frequency looses

amplitude. If the sample is fieely vibrating, ie

when the sample is suspended in the nodes of

the investigated vibration mode, then this

amplitude loss is due to internal friction or

material damping.

In

the case of rectangular

bar samples, the procedures described in

ASTM C 1259

-

94 enabled

us

to calculate

the E-modulus

of

the material from the

bending frequency of the bar.

Materials

NGK

Ceramics Europe supplied silicon

nitride combustion engine valves (SN73K

grade) for high temperature characterisation

with impulse excitation. The impulse

excitation response of these ceramic valves

has been compared with that of standard, steel

alloy engine valves, ‘explanted’ from a

commercial car engine.

Further, small rectangular bars of in-

house hot-pressed silicon nitrides with

different sint ering additives were compared.

Details of the powder preparation and

sintering parameters are given in [6]. The

starting materials used to prepare the powder

mixtures are commercial Si3N4, Y2O3 and

A1203 powder. One grade (SNA14) was

prepared with 4wt% A1203.

A

second grade

(SNYS)

contained

8

wt%

Y203. The third

grade (SNY6A12) was sintered with a mixture

of

Y203

(6

wt%)

and A1203 (2

wt%).

The hot-

pressed disks were machined into suitable

samples for IET (nominally 30

x

5

x

2

mm3).

In

addition,

two

grades of hot-pressed

tetragonal

ZrO2

polycrystalline

(TZP)

ceramics were tested. The preparation of these

materials has been described in [7]. The first

grade (3Y-TZP) was prepared by hot-pressing

218

1

0.95

.

...

~

0015

c

0

r

5

001

-

E

om-

c

-

+

steel

alloy

valve

*

silicon

nitnde valve

-

--

0.75

4

j

100

300

5w

700

900

Temperature

('C)

Figure

2

Comparison of the change of resonance

frequency of ceramic and steel alloy engine

valves with temperature.

Tosoh TZ-3Y powder. The second grade

(2YM-TZP) was obtained by hot-pressing in a

similar way a mixture of Tosoh TZ-3Y

powder and Tosoh TZ-0 powder, to obtain an

overall Y2O3 content of 2.5 mol%.

RESULTS

Effect of temperature

on

the stiffness and

damping of combustion engine valves

.

Both silicon nitride and steel alloy

engine valves were tested in the graphite

furnace in a N2-atmosphere. The valve,

suspended by graphite threads as shown in

Fig.

lb,

is excited approximately halfway

along the length of its stem. The major

bending resonance frequency

of

the ceramic

outlet valve (valve head diameter 31

mm,

length 104 mm)

is

near 10

kHz.

The steel

engine valve (valve head diameter 24

mm,

length 92mm) has a major resonance

frequency near 7

kHz.

In

Figure 2, the relative

change of these frequencies with increasing

temperature is shown, up to a typical

maximum operating temperature of the outlet

valves (900°C). Whereas the stifhess

of

the

ceramic valve is hardly affected in this

temperature range, the E-modulus

of

the steel

alloy valve changes by a factor

of

about

0.8

x

0.8

=

0.64 (taking into account the quadratic

relation between E-modulus and resonance

frequencies)

.

Figure 3 shows the change

of

the

internal friction in the silicon nitride valve

with increasing temperature. The internal

friction is very low until 800°C. From this

temperature

on,

damping increases rapidly,

until it reaches a value which is higher than

Figure

3

Internal friction in silicon nitride engine

valve

as

a function of temperature, indicating the

existence of a damping peak near

1000°C

with a

maximum value larger than can be measured with

IET (upper limit

1.5%).

the upper damping value measurable with

IET. This upper limit value depends on

sample geometry and material, and appears to

be about 1.5% for the investigated engine

valve. At a temperature of about llOO°C,

damping has decreased and can be determined

again. All together, the data mark the

existence of a large damping peak centred

near 975°C.

Effect

of

sintering additive composition

on

damping in Si3N4

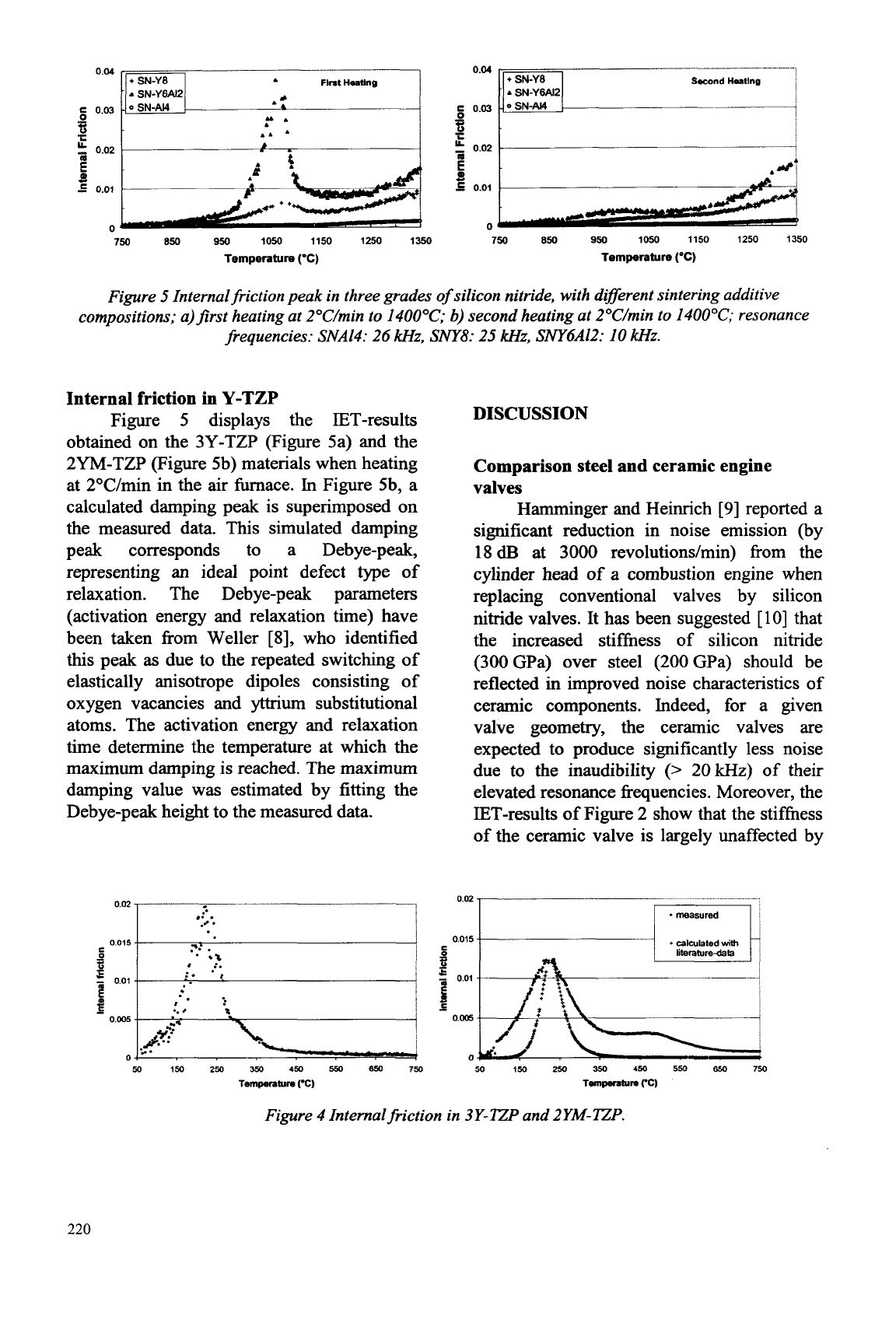
Figure 4 compares the level of internal

friction between 75OOC and 135OOC in three

hot-pressed silicon nitrides. The SNA14

material-data do not reveal a damping peak.

Internal friction does increase slowly from

about 1100°C. The

SNY8

silicon nitride is

characterised by a small but distinctive

internal friction peak near 1070°C. At

approximately the same temperature a much

larger damping peak occurs in the SNY6A12

silicon nitride, sintered with a mixture

of

Y203 (6wt%) and A1203 (2wt%). The

internal friction peaks are superimposed on an

exponentially increasing background. It can

be observed that, in the investigated cases, a

large background coincides with a high

internal friction peak. Figure 4b displays the

results obtained during a second heating.

Clearly, the first temperature cycle (at

2"C/min to 1400°C) has affected the

material's response: the internal friction peaks

have decreased.

219

I

004

-

004

+

SN-YB

Flnt

Heaths

I

c

0

03

0

.:

-

A

SN-Y6A12

g

003

-,OSN-AM

2

002

11

P

002

b

I.

A

u.

3

r

E

5

e!

001

~~~~

E

001

Figure

5

Internal friction peak

in

three grades

of

silicon nitride, with diflerent sintering additive

compositions; a)first heating at 2"C/min to 1400°C;

b)

second heating at 2OC/min to 14OOOC; resonance

frequencies: SNA14: 26

kHz,

SNY8:

25

kHz,

SNY6A12:

I0

kHz.

I

-

__--

-

- -

--

-

+

SN-YB Second Heating

.

A

SN-YW2

-

0

SN-AM

-

I

l

it

-

Internal friction in

Y-TZP

Figure 5 displays the IET-results

obtained on the 3Y-TZP (Figure 5a) and the

2YM-TZP (Figure 5b) materials when heating

at 2OC/min in the air furnace.

In

Figure 5b, a

calculated damping peak is superimposed on

the measured data. This simulated damping

peak corresponds to a Debye-peak,

representing an ideal point defect type of

relaxation. The Debye-peak parameters

(activation energy and relaxation time) have

been taken from Weller [8], who identified

this peak

as

due to the repeated switching of

elastically anisotrope dipoles consisting

of

oxygen vacancies and

yttrium

substitutional

atoms. The activation energy and relaxation

time determine the temperature at which the

maximum damping is reached, The maximum

damping value was estimated by fitting the

Debye-peak height to the measured data.

DISCUSSION

Comparison steel and ceramic engine

valves

Hamminger and Heinrich [9] reported a

significant reduction in noise emission (by

18

dB

at 3000 revolutions/min) from the

cylinder head

of

a combustion engine when

replacing conventional valves by silicon

nitride valves. It has been suggested

[

101

that

the increased stiffness of silicon nitride

(300GPa) over steel (200 GPa) should be

reflected in improved noise characteristics of

ceramic components. Indeed, for a given

valve geometry, the ceramic valves are

expected to produce significantly less noise

due to the inaudibility

(>

20kHz)

of

their

elevated resonance fkequencies. Moreover, the

IET-results of Figure 2 show that the stiffness

of

the ceramic valve is largely unaffected by

-

measured

*calculatedwiih

literaturedata

-

50

150

250

350

450

550

650

750

50

150

250

350

450

550

650

750

Tempmtun

('C)

Temp.Rtum

rc)

Figure 4 Internal friction in 3Y-ZP and 2YM-ZP.

220

temperature within the range of normal valve

operation. Steel, on the other hand, does loose

1/3 of its stiffness between room temperature

and

900OC.

The IET-results therefore indicate

that the advantages of high stiffness become

even more pronounced at more elevated

operation temperatures.

The damping peak, which happens to

occur near the operation temperature of the

outlet valve head, also affects the noise

produced by the valve. The origin of the

characteristic damping peak near 1000°C is

known to be the glass transition of

intergranular pockets

of

amorphous silicate

phases

[

111. The internal friction or vibration

energy dissipation at this T,-peak can reduce

the noise produced by the valves. At

temperatures near or below the T,-peak, the

behaviour of the silicon nitride is unaffected

by creep deformation. Therefore, the

intentional operation of the valve in the

temperature region of the T,-peak can be

considered safe practice, and could be

exploited in other vibration-critical

applications.

Comparison

of

SNA14,

SNYS

and

SNY6A12

The IET-results shown in Figure4

demonstrate the effect of the use of different

additives on the high-temperature structural

performance of silicon nitrides. The SNA14

does not show a T,-peak. According to the

work of Donzel

[ll]

this implies that this

grade is free of amorphous glass pockets.

Indeed, it is

known

that the used composition

leads to the formation of a sialon material, in

which A13+ ions are substituting for Si4+. To

maintain electrical neutrality the o2--ions

enter the Si3Ns lattice

as

well and substitute

for the N atoms. The incorporation of the

oxygen atoms decreases the amount of

intergranular silicate glass, and renders the

sialon material highly creep resistant.

The comparison of the internal friction

curves of the

SNY8

and SNY6A12 materials

reflects the different crystallinity of their

intergranular phases. The height of the

damping peak of the SNY6A12 material

indicates that the amount of residual

intergranular pocket phase is larger than in the

SNY8

material. XRD-investigation

of

the

materials in the

as

hot-pressed state [6],

confirms the presence

of

a crystalline

intergranular phase (Y-N-apatite) in

SNY8,

while the SNY6A12 material contains only

a-

and p-Si3N4.

Although creep tests have not been

performed on the three tested silicon nitride

grades, it can be inferred from literature that

the creep resistance of the three grades ranks

in the same way

as

the internal friction T,-

peak height. Monophase sialon indeed is more

creep resistant than the materials with

intergranular residues of the sintering

additives. Also, the creep resistance is

increased by the (partial) crystallisation of the

intergranular phase. However, since the

internal fiiction peaks are caused by

relaxation phenomena with limited amplitude,

there is no direct micromechanical relation

between the T,-peak and creep resistance.

Schaller has shown that the exponentially

increasing background, which is due to

microplastic deformation, correlates better

with creep resistance [12]. In the silicon

nitride grades we have studied, the ranking

according to peak height and according to

background coincide. However,

this

ranking

can be affected due to grain morphology and

intergranular phase distribution.

Figure 4b shows internal fiction during

the second heating up to 1400°C. The

damping peak is significantly reduced for both

SNY8

and SNY6A12 materials, but the

background

is

largely unaffected. In-situ high

temperature X-ray dimaction

[

61 confirms the

crystallisation of the intergranular pockets.

Comparison

of

3Y-TZP and 2YM-TZP

The internal friction data show a peak

near 2OOOC for both the 3Y-TZP and 2YM-

TZP samples. The location

of

this peak

depends slightly on the resonance frequency

which was

7

kHz

for the

3Y-TZP

and 14

kHz

for the 2YM-TZP. Otherwise, the peaks are

comparable

as

both are caused by elastic

dipole relaxation

[

81. At temperatures above

the dipole peak the

two

material grades

behave differently. The 3Y-TZP is

known

to

be fully stable and resistant to thermally

induced transformation of the tetragonal to the

monoclinic phase. The 2YM-grade, due to the

22 1

Heinrich J.G., Aldinger F. (Eds.) Ceramic Materials and Components for Engines

Подождите немного. Документ загружается.