Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

950 M.P. Nikiforov and D.A. Bonnell

challenging, usually requiring 2D or 3D numerical approaches.

89–92

Note that SCM distinguishes the difference between n- and p-dopants

in the sample, whereas SSRM does not. On the other hand metallic and

insulating samples give no contrast in an SCM image, while SSRM

images defects in insulations and in metallic ﬁ lms.

Another technique for electronic property characterization on the

nanoscale is scanning gate microscopy (SGM). SGM is a two-scan

technique. During the ﬁ rst scan topography of the sample is monitored

in intermittent contact mode. During the second scan an ac voltage is

applied across the sample; a biased tip is brought within proximity of

the sample, and the magnitude of the current across the sample is mea-

sured as a function of tip position. The ﬁ rst implementation of SGM

was demonstrated on a single wall carbon nanotube in 2000.

The tip

acted as a gate electrode in this nanotube circuit. It was found that the

Fermi surface of the nanotube was not uniform along its length.

University of California at

Berkeley

and University of Pennsylvania

96,97

used SGM to good effect

in nanotube-based electronic circuits illustrating the ability to quantify

local properties in individual nanotubes and to demonstrate threeter-

minal device behavior. Recently researchers from the University of

California at Irvine

measured the gating effect of a biased AFM tip

on ZnO nanowires and found it to be 200 times smaller than that of

single-wall carbon nanotubes.

The change of resistance in these

nanowires differs because of the difference in the widths of the single-

wall carbon nanotube (1–2 nm) and ZnO nanowires (∼400 nm).

Research in the group of R.M. Westervelt extended the concept of

using an SPM tip as a perturbing probe to visualize the ﬂ ow of electron

waves in a two-dimensional electron gas. They produced a planar

electron gas 57 nm below the surface in a GaAs/AlGaAs heterostruc-

ture with a quantum point contact formed with a pair of gates on the

surface. A biased tip near the surface will capacitively couple to the

underlying electron gas. As the tip is scanned across the surface, it

decreases the conductance through the contacts when it is over a region

of high electron ﬂ ow and has no effect over a region with low electron

ﬂ ow. Similar to SGM, the image is the current or conductance across

the gap as a function of tip position on the surface. Figure 14–15 illus-

trates the geometry of the quantum point contact and the pattern of

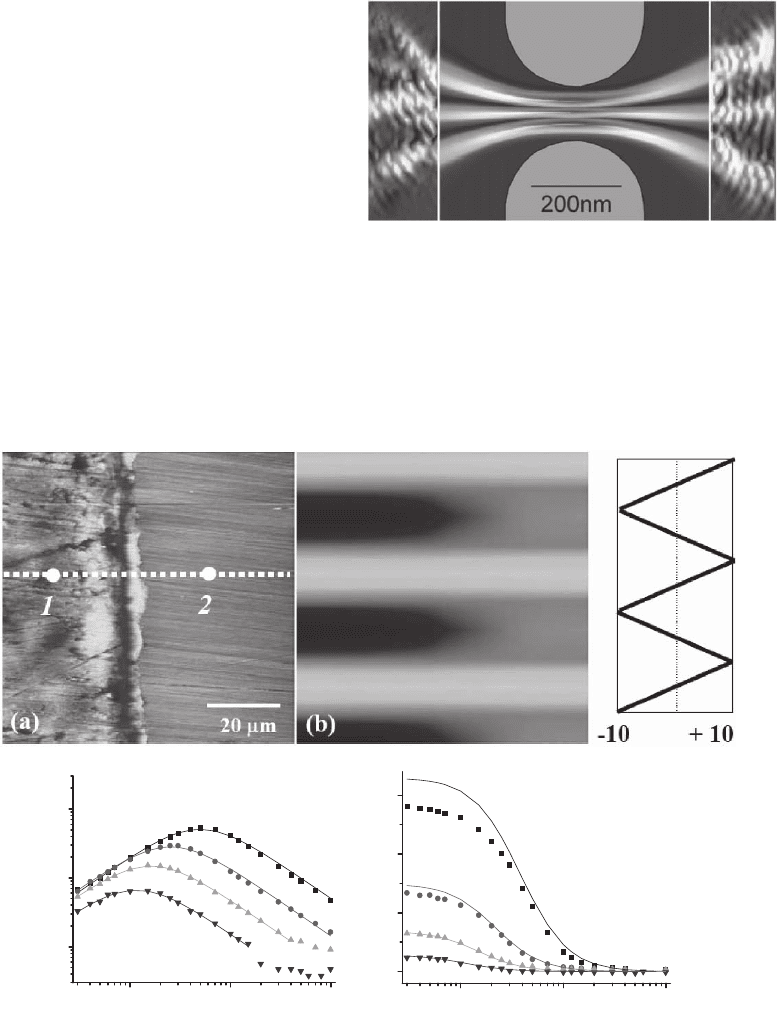
electron ﬂ ow that results from a system with a density of 4.5 × 10

−2

a mobility of 1 × 10

/V s, a mean free path of 11 µm, and a Fermi

wavelength λ

= 37 nm. Images were recorded with the sample and the

SPM at T = 1.7 K.

Many phenomena underlying materials behavior involve time-

dependent processes that could be accessed if signals applied to the

sample and/or tip spanned a wide frequency space. The ﬁ rst introduc-

tion of frequency dependence in scanning probes is referred to as

scanning impedance microscopy (SIM).

This is a noncontact, ﬁ rst

harmonic detection in which the oscillating electrical signal is applied

to the sample instead of the tip. The implementation of SIM is com-

pared to SSPM in Figure 14–11. The tip can act as a nonperturbing

probe or as a local gate in a conﬁ guration that allows both the ampli-

tude, which is related to potential, and the phase, which is related to

Researchers from Stanford University,

Chapter 14 Scanning Probe Microscopy in Materials Science 951

loss, to be quantiﬁ ed. The frequency dependence can be used to isolate

relaxation associated with electron traps at interfaces and defects.

Figure 14–16a and b illustrates SIM of an interface and grain bound-

ary. For a prototypical ideal sample composed of a single electroactive

Figure 14–15. Experimental images (outside)

and theoretical simulations (inside) of the ﬂ ow

of electron waves through a quantum point

contact. Fringes spaced by half the Fermi wave-

length demonstrate coherence in the ﬂ ow.

[Courtesy of Westervelt et al. Reproduced with

permission from Physica E, 24, 63–69, 2004.] (See

color plate.)

-2

-1

tan(

)

Frequency (Hz)

1.0

1.5

2.0

2.5

Amplitude ratio

Frequency (Hz)

(c)

(d)

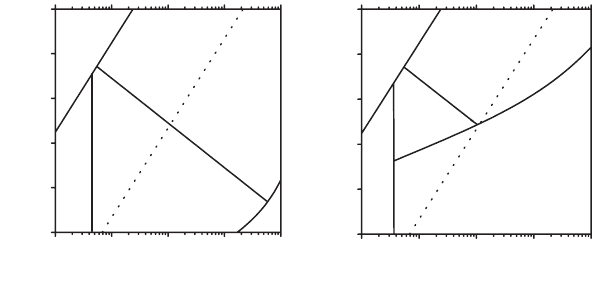
Figure 14–16. Surface topography (a) of the cross-sectioned diode. The potential proﬁ les were acquired

along the dotted line. The changes of potential, phase, and amplitude were determined from positions

1 and 2. Surface potential (b) during a 0.002-Hz triangular voltage ramp to the sample for R = 500 Ω.

The scale is 300 nm (a) and 10 V (b). (c) Frequency dependence of SIM phase shift and (d) amplitude

ratio of grain boundary in an Nb-doped Σ5 SrTiO

bicrystal. Solid lines on (c) are ﬁ ts for frequency

independent grain boundary resistance and capacitance and on (d) the calculations are from using

interface resistance and capacitance from phase data. Data are shown for circuit terminations 148 Ω

(䊏), 520 Ω (䊉), 1.48 kΩ (䉱), and 4.8 kΩ (䉲). (Courtesy of Kalinin and Bonnell. Reprinted with permis-

sion from Physical Review B 70, 235304, 2004).

952 M.P. Nikiforov and D.A. Bonnell

interface with resistance, R

, and capacitance, C

, in series with two

current-limiting resistors, R, the phase shift across the interface as a

function of frequency is tan(ϕ

) = (ωC

)/(R + R

) + Rω

, where

ω = 2πf and f is the oscillation frequency. See Figure 14–11 for the

exact conﬁ guration. For high frequencies the interface phase shift

has the simple form tan(ϕ

) = 1/ωC

R and interface capacitance can

be calculated directly from the frequency shift. At low frequencies the

amplitude ratio across the interface, A

= (R + R

)/R. In addition, a

dc potential can be applied across the surface establishing a potential

step at the interface, which can then be measured by SSPM. As the dc

bias across the interface of a metal/silicon diode is switched from

positive to negative, the forward/reverse bias behavior is evident in

the potential image (Figure 14–16a). The phase image of an atomically

abrupt SrTiO

grain boundary (Figure 14–16b) shows the large effect

of a 2D defect. The frequency dependences of both the amplitude

(which is related to potential) and phase shift (which is related to

interface processes) of the SrTiO

boundary are shown in Figure 14–16c

and d. The combination of SIM and SSPM allows local transport

spectroscopy of individual interfaces, e.g., direct measurement of

the spatially resolved interface C–V characteristics. The quantitative

nature of this approach has been conﬁ rmed on studies of Si/metal

diodes.

100

SIM also contains an intrinsic improvement in spatial resolution

relative to scanning surface potential or SGM. In combination with

other SPM techniques, SIM has been used to map the rectifying behav-

ior of a Schottky junction, and characterize defect-mediated transport

in a single nanotube,

as well as provide transport measurements of

idealized grain boundaries. Recently SIM was used to image current

transport in carbon nanotube networks imbedded in a polymer.

101

Similar to SSPM, the spatial resolution in SIM is ultimately limited by

capacitive tip–surface interactions.

A second approach to accessing frequency-dependent transport

expands the frequency range to eight orders of magnitude and pro-

vides higher spatial resolution. Nanoimpedance microscopy and spec-

troscopy (NIM)

102–104

is a contact probe with force feedback, in which

the oscillating bias signal is applied to the tip; current phase and

amplitude are detected at the sample. Figure 14–17a illustrates the local

impedance between a tip and lateral electrode, across a ZnO grain

boundary. By accessing this range of frequencies, the data can be pre-

sented in a conventional Cole–Cole plot that describes both the real

and imaginary components of impedance. In these plots each of the

semi circles corresponds to the properties of a microstructural element.

The interpretation is somewhat model dependent, but for sample con-

ﬁ gurations such as thin ﬁ lms with bottom electrodes or single bound-

aries between electrodes, quantitative characterization of the local

properties is possible. The local boundary potential, capacitance,

charge, and depletion lengths can be extracted with spatial resolution

on the order of tens of nanometers. In a conﬁ guration with an electrode

under the sample, the impedance of individual grains can be imaged,

as shown in Figure 14–17b.

Chapter 14 Scanning Probe Microscopy in Materials Science 953

3.2 Advanced SPM Techniques for Dielectric Properties

In principle, utilizing higher order harmonic signals and clever detec-

tor design allows dielectric constant, electrostriction, and piezoelectric

properties to be detected (Table 14–2). In practice a number of probes

have been developed to quantify linear and nonlinear dielectric prop-

erties locally. These have focused on electromechanical coupling coef-

ﬁ cients, hysteretic ferroelectric domain switching, etc.

PFM is a scanning probe that is used increasingly to determine

electromechanical coupling coefﬁ cients at local scales. It is a contact,

electrically driven probe technique with feedback based on phase lag.

Like NIM, an oscillatory electric ﬁ eld is applied to the tip, which is in

contact with the sample (Figure 14–18). If the material is piezoelectric,

1x10

2x10

3x10

4x10

0.0

5.0x10

1.0x10

1.5x10

2.0x10

-Z

(Ω

)

(Ω)

Figure 14–17. (a) Cole–Cole plot of local impedance spectra between the SPM

tip and the top electrode (nanoimpedance spectroscopy) at tip/sample biases

of +5 V (䊉), +3 V (∆), and +2 V (♦) for ﬁ xed tip location. Solid line is the ﬁ tting

of impedance data to the equivalent circuit of two RC elements in series (——).

Note that interface resistance decreases with dc bias, indicative of varistor

behavior. (b) Representative NIM phase image; the dark region corresponds

to nonconductive inclusion in the sample (phase θ = −90°).

V = V

+ V

sin(ωt)

Figure 14–18. Working principle of PFM. An ac bias is applied to the tip,

which his in contact with the sample, and an electric ﬁ eld is generated. If the

material is ferroelectric the size of the region around the tip will change. A

schematic of the responses of polarized domains is presented in the inset.

954 M.P. Nikiforov and D.A. Bonnell

the ﬁ eld results in a local deformation of the surface that oscillates the

tip, i.e., piezoresponse (PR).

105,106

In a ferroelectric material domains

with downward polarization vector contract with a positive voltage,

producing a phase shift of δ = 180°. For upward oriented domains, the

situation is reversed, and δ = 0°, because the deformation is in phase

with the ﬁ eld. The phase, therefore, indicates the orientation of polar-

ization. The piezoresponse amplitude, A = A

1ω

, deﬁ nes the magni-

tude of the interaction. For the ideal case of a (100) surface of a tetragonal

compound, A = αd

, where α is proportionality coefﬁ cient close to

unity,

107

the piezoelectric constant, d

, is related to the polarization, P,

as d

= εε

P, where Q is the second-order electromechanical coefﬁ -

cient. For the general case there are in-plane components of polariza-

tion that can be accessed by measuring the lateral response of the tip

to a ﬁ eld variation.

108,109

Furthermore, the piezoelectric response is a

tensorial function, the complexity of which depends on the symmetry

of the compound and the orientation of the grain or crystal. Harnagea

et al.

110

have shown that even for BaTiO

with relatively high symmetry

either the grain orientation or the in-plane component must also be

known to determine domain orientation.

This is illustrated nicely by Gruverman and co-workers

111

who under-

took the three-dimensional high-resolution reconstruction of the polar-

ization vectors in a (111)-oriented Pb(Zr,Ti)O

ferroelectric capacitor by

detecting the in-plane and out-of-plane polarization components using

PFM. Figure 14–19a and b shows the vertical and lateral contributions

to the phase images of a region that is nominally poled in the vertical

direction. In spite of exhibiting uniform vertical contrast, the lateral

component exhibits signiﬁ cant variation. Knowing that this material

is oriented in the (111) direction, the individual domain orientation can

be determined, as shown on Figure 14–19c. In this case the vertical

components of domains polarization have the same magnitude, while

the lateral component varies between domains.

In PFM voltage spectroscopy,

112

piezoresponse, A

1ω

, and phase, f, are

measured as a function of dc potential offset, V

, on the tip.

109,113

PFM

spectroscopy yields local electromechanical hysteresis loops, quantify-

ing remnant response and coercive bias, on the 20–50 nm level. Piezo-

response force spectroscopy of PbTiO

is illustrated in Figure 14–20.

These hysteresis curves are acquired on a PbTiO

ﬁ lm with 100 nm grain

size. The phase signal is related to polarization and therefore has the

shape of a conventional P–E hysteresis curve. The amplitude signal

shows that strain, in addition to switching, occurs with voltage and

again traces the conventional butterﬂ y shape of a curve. These curves

illustrate the critical tip bias required to achieve polarization switching.

A number of attempts to relate local hysteresis to crystallographic ori-

entation and piezoresponse amplitude have been reported.

114

One critical issue with regard to quantiﬁ cation and spatial resolution

limit is the question of what volume is accessed by PFM. The answer

is found by determining the decay of the electric ﬁ eld below the probe

tip, which in turn depends on the dielectric constant and conductivity

of the material. For oxide ferroelectric compounds the volume in on

the order of 20–200 nm.

115,116

Consequently, for ﬁ lms thinner than this,

Chapter 14 Scanning Probe Microscopy in Materials Science 955

Figure 14–19. Investigation of a PZT capacitor with vertical and lateral force

PFM. Images of amplitude (a) and phase (d) in vertical PFM and amplitude

(b) and phase (e) in lateral PFM are presented. (c) Schematics of the domain

orientation in the sample followed from PFM measurements. Note that only

a combination of three PFM modes gives complete information about the

direction of the polarization vector in the sample (only two are presented on

the picture). [Courtesy of Rodriques et al. Reproduced with permission from

Journal of Applied Physics, 95(4), 1958–1962, 2004.]

Figure 14–20. (a) Vertical

phase and (b) amplitude hys-

teresis loops of PbTiO

thin

ﬁ lms. (Courtesy of Gruveman

and co-workers. Reprinted

with permission from Journal

of Applied Physics, 92, 2734,

2002).

956 M.P. Nikiforov and D.A. Bonnell

or inclined domain structures, quantiﬁ cation requires accounting for

this volume.

The question arises as to whether the PFM inﬂ uences the properties

it is measuring. Recently, it was shown that the mechanical strain pro-

duced by the tip can suppress local polarization

117

or induce local fer-

roelectroelastic polarization switching.

118,119

A quantitative analysis of

the tip-induced potential and stress distribution is required to charac-

terize local ferroelectric properties by SPM.

120–124

A rigorous treatment

of the image contrast includes simultaneous electrostatic and electro-

mechanical interactions. One complication in PFM is that both long-

range electrostatic forces and the electroelastic response of the surface

contribute to the PFM signal.

63,125

Even under optimal conditions, the

basis of the electroelastic contribution, A

piezo

, is not straightforward

because of the complex geometry of the tip–surface junction. Some prog-

ress in the quantitative understanding of PFM has been achieved.

126–129

Depending on the tip radius of curvature and the indentation force,

PFM may correspond to the electroelastic response of the surface

induced by the contact area (strong indentation limit) or be dominated

by the electroelastic response of the surface due to the ﬁ eld produced

by the spherical part of the tip (weak indentation limit). In these cases,

the magnitude of surface and tip displacements is determined by the

electromechanical coupling in the material. Alternatively, the signal

can be dominated by the electrostatic tip–surface interactions (electro-

static limit) and have little relation to the properties of the material.

Taking an approach familiar to materials scientists, the analytical solu-

tions of these interactions can be presented as contrast mechanism

maps that relate experimental conditions to properties of the material

and delineate the conditions under which quantitative measurements

can be obtained (Figure 14–21).

126

The relationship between higher order harmonics of the PR function

and time dependence of domain switching has been developed into a

probe of switching dynamics called second harmonic piezo force

microscopy (SH-PFM).

130

When the ﬁ eld and the measured electrostric-

tive strain are in the z direction, electrostriction is expressed in terms

of the ﬁ eld-induced polarization P as x = Q

. For a ferroelectric with

spontaneous polarization P

and ﬁ eld-induced polarization P

, the

strain becomes x = Q

)

+ 2Q

+ Q

)

, where the second and

third terms are the piezoelectric response (because d

= 2Q

/ε) and

the electrostrictive response, respectively. Under external ﬁ eld, E

(ω) =

cos ωt, induced

xQ P

QPP t Q P t=+













33 33

2()

()

SE E

cos cosωω

In macroscopic measurements electrostriction is quantiﬁ ed with inter-

ferometry.

131,132

In SH-PFM the cantilever oscillation in contact mode

determines the local electrostrictive properties.

A complementary strategy to accessing linear and nonlinear dielec-

tric properties is referred to as scanning nonlinear dielectric micro-

scopy

133,134

and near-ﬁ eld microwave micro-scopy (NFMM).

135,136

The

Chapter 14 Scanning Probe Microscopy in Materials Science 957

approach utilizes a coaxial probe in which a sharp, center conductor

“tip” protrudes. The probe is actually the end of a transmission line

resonator, which is coupled to a microwave source. The concentration

of the microwave ﬁ elds at the tip changes the boundary condition of

the resonator, and, hence, the resonant frequency and quality factor.

The magnitude of the perturbation depends on the dielectric proper-

ties of the sample. Speciﬁ cally, the change in resonant frequency, ∆ f

= g∆ε′, where g is a constant and ∆ε′ is the real part of the complex

dielectric constant; ∆(1/Q) = q∆ε″, where q is a constant and ∆ε″ is the

imaginary part of the complex dielectric constant. The spatial resolu-

tion of the microscope in this mode of operation is about 1 µm. NFMM

with coaxial resonators has been used successfully to quantitatively

image sheet resistance, dielectric constant, dielectric polarization,

topography, magnetic permeability, and Hall effect. Lu et al.

137

have

used NFMM on ferroelectrics (001) LiNbO

single crystal to distin-

guish variations in dielectric constant and ferroelectric domains (Figure

14–22). The growth process of this crystal results in a periodic composi-

tion change that should alter the local dielectric constant. Different

ferroelectric domains in this crystal have the same dielectric constant.

The two periodic variations in composition and ferroelectric domain

orientation are not coincident. Since ∆ f

relates to dielectric constant

and ∆Q relates to loss associated with ferroelectric domain boundaries,

the images should demonstrate different periodicities. This is illus-

trated in Figure 14–22a and b. Lu et al.

137

claimed that their NFMM has

submicrometer lateral resolution, so the prognosis for further improve-

ment of special resolution is good. Lee and Anlage

138

demonstrated that

high-order harmonic powers acquired by NFMM can be used to spa-

tially resolve the local nonlinearity. In their work, the grain boundary

-1

Indentation force (nN)

Tip radius (nm)

CSI

-1

Indentation force (nN)

Tip radius (nm)

(b)(a)

CSI

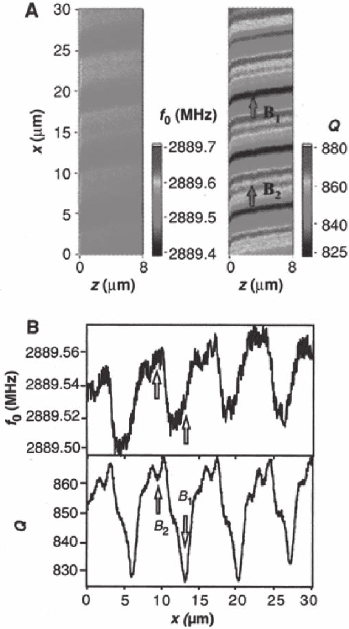
Figure 14–21. Contrast mechanism maps of piezoresponse force microscopy.

SI, strong indentation regime; CSI, contact-limited strong indentation; WI,

weak indentation regime; NE, nonlinear electrostatic regime; NL, nonlocal

interactions; PD, plastic deformation. The dotted line delineates the region

where stress-induced switching is possible. (a) w = 0.1 nm, ∆V = V

tip

− V

= 0 V;

(b) w = 0.1 nm, ∆V = 5 V. (Courtesy of Kalinin and Bonnell. Reprinted with

permission from Physical Review B, 65, 125408, 2002.)

958 M.P. Nikiforov and D.A. Bonnell

area of superconducting YBCO thin ﬁ lm deposited on an SrTiO

bicrys-

tal was spatially resolved from the ratio of the second and the third

power.

4 Future Trends

The rapid pace of advances in SPM shows no sign of slowing. Atomic

resolution imaging is becoming ever more common and the range of

local properties that can be quantiﬁ ed is expanding. In the next few

years, several areas of research will likely push the limits of SPM even

further.

Combinations of multiple modulations and high order harmonics

will continue to be used in new ways to access complex properties.

Table 14–2 illustrates the potential of such combinations but is not a

comprehensive list of all possibilities. Neither the advanced magnetic

probes nor the near-ﬁ eld optical probes are included. Frequency mixing

has not yet been exploited.

There is recent evidence that some of the property probes may

achieve atomic resolution. Eguchi et al. obtained atomic scale imaging

in an SPPM (KFM).

139

Figure 14–23 compares NC-AFM and SSPM of a

Ge/Si (105) surface with a model of the atomic structure. An in another

Figure 14–22. (A) Images of

the proﬁ les of periodic dielec-

tric constant (on the left) and

ferroelectric domain boundar-

ies (on the right). (B) Line pro-

ﬁ les of frequency (top) and

quality factor (bottom) images.

(See color plate.)

Chapter 14 Scanning Probe Microscopy in Materials Science 959

community, Rugar et al. demonstrated the measurement of a single

spin of an electron.

140

While further work is needed to conﬁ rm the

absence of artifacts in these measurements, these observations are

exciting in that they portend a future of atomic resolution property

imaging. Advances in high precision cantilevers and tips could unite

NC-AFM imaging of structure with similar resolution imaging of

potential, work function, dielectric function, etc. Concomitant advances

in the physics of tip–surface interactions will be necessary when we

need to interpret, for example, atomic resolution “dielectric constant.”

Finally, in the ideal world it would be useful to combine multiple

probes with a variety of options for sample stimulation for comprehen-

sive analysis. This vision is schematically illustrated in Figure 14–24.

Scanning probes with multiple transport-related tips are commercially

NC-AFM

KFM

STM

Figure 14–23. Atomic resolution NC-AFM, STM, and KFM on Ge/Si (105).

[Courtesy of Eguchi et al. Reproduced with permission from Physical Review

Letters, 93(26), 2004.] (See color plate.)