Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

808 S.W. Hell and A. Schönle

SWM, it is impossible to remove the interference artifacts on a general

basis.

While an in-depth analysis of nonlinear iterative deconvolution (i.e.,

image restora-tion) algorithms is far beyond the scope of this chapter,

it can be safely stated that these suffer from limitations similar to the

linear deconvolution approaches. They cannot really restore informa-

tion that has been lost in the imaging process. A connected and largely

convex OTF that does not imply regions of weak transmission is almost

equally important to these algorithms. Non linear iterative algorithms

take advantage of a priori information about the object that linear

deconvolution cannot uncover unambiguously. The simplest a priori

information is the positivity of the object and of the image. Carefully

applied to 4Pi and I

M data, nonlinear restoration can yield impressive

results, but extreme care must be taken not to compromise the reli-

ability of the outcome by false or even biased assumptions.

3.3 Discussion: Improved Axial Resolution in Practice

While the use of coherent beams from two opposing lenses extends

the OTF in the axial direction, a detailed analysis shows that conditions

have to be met to exploit this advantage in an effective manner. Reliable

and artifact-free restoration is possible only if the region of the OTF is

convex, that is, if it does not contain nonnegligible “weak” regions or

gaps. It was shown that the OTF of an SWM exhibits marked gaps

along the optic axis that make the removal of the interference artifacts

almost impossible. It is therefore not surprising that previous experi-

mental studies conﬁ rmed that in the SWM it is impossible to unam-

biguously distinguish two axially separated objects, unless the object

is thinner than 50% of the wavelength.

Unambiguous resolution of

axially extended objects is impossible with SWM for fundamental

physical reasons. Nevertheless, both SWM and 4Pi microscopy have

been successfully applied to the ultraprecise measurement of axial

distances (Albrecht et al., 2002; Schneider et al., 2000; Schmidt et al.,

2000) and object sizes (Egner et al., 2000; Failla et al., 2002), which is

conceptually and practically less demanding.

The OTF of the I

M is superior to that of the SWM, because it remains

nonzero throughout its support. Still, it is weak over a considerable

region when compared to the giant zero-frequency peak, which actu-

ally is a singularity. Hence, to beneﬁ t from this contiguity, I

M data

must be recorded with a very large signal-to-noise ratio. Besides, the

method may be applicable to sparse nonextended objects only, such as

points or sparse ﬁ ne lines. The OTF of the reported 4Pi microscopes

are truly contiguous. In the critical regions, the 4Pi confocal OTF

(Figure 12–4) exhibits signiﬁ cant values in the 19–23% range. This

feature is of key relevance to the removal of the interference artifacts

and hence for unambiguous, object-independent 3D microscopy with

improved axial resolution.

Another major difference between the effective PSF of the SWM and

M on the one hand, and the 4Pi confocal on the other, is the fact that

the PSF is spatially much more conﬁ ned in the latter case. This allows

Chapter 12 Nanoscale Resolution in Far-Field Fluorescence Microscopy 809

us to reduce the process of lobe removal from a 3D deconvolution to a

one-dimensional linear problem with the highly useful side effect that

single layers can be acquired and deconvolved while all other methods

require acquisition of a full 3D data stack.

The 4Pi concept is the result of rigorously maximizing the aperture

angle employed in the imaging process. This results in a superior exci-

tation OTF due to its lateral ﬁ lling, which is rooted in the fact that the

(exciting and detected) light is focused. Hence, while scanning with a

focused beam inevitably reduces imaging speed, this procedure also

results in fundamentally improved imaging properties of the micro-

scope. Flat ﬁ eld standing wave excitation inherent to the I

M and SWM

trades off collected spatial frequencies. The loss of optical frequencies

is so signiﬁ cant (Figures 12–3 and 12–4) that the ability to provide

unambiguous axial resolution is either put at risk or not viable.

Nevertheless, axial resolution improvement and imaging similar to

the 4Pi microscope are reportedly possible when combining I

M with

ofﬂ ine image restoration (Gustafsson et al., 1999). The combination of

M with fringe pattern illumination and subsequent image restoration

has also been suggested to (1) alleviate the problem of the zero frequency

singularity (Gustafsson, 2000; Heintzmann and Cremer, 1998) and (2) to

increase the lateral resolution to that of (restored) confocal microscopy.

Leaving aside the technical complexity of controlling the interference

patterns of typically four pairs of beams, this suggestion conﬁ rms that

an unambiguous axial resolution requires the employment of a wider

angular spectrum. In fact, the spherical beams in a 4Pi microscope can

be regarded as a complete spectrum of interfering plane waves coming

from all angles available. Hence, from the standpoint of imaging theory,

the combination of I

M with fringe pattern illumination is a modiﬁ ca-

tion of I

M toward a scheme that is more similar to the 4Pi arrangement;

the improvements of the OTF are gained by conditions that converge to

the “focusing” conditions found in the 4Pi microscope.

In real samples the OTF of the microscopes is compromised by aber-

rations that were not included in our comparison of the concepts.

Residual misalignments of the foci induced by variations of the refrac-

tive index in the sample play a role. However, successful 4Pi imaging

of the mouse ﬁ broblast cytoskeleton (Nagorni and Hell, 1998) and I

imaging of similar structures (Gustafsson, 2000) have revealed that

aberration effects are surmountable. Image deconvolution requires

prior knowledge of the PSF and hence its explicit determination with

a point-like object. This is particularly important since the PSF depends

on the relative phase of the two counterpropagating wavefronts. It has

been shown that in 4Pi microscopy the type of interference in the focal

plane (constructive, destructive, or anything in between) is of lesser

importance (Hell and Nagorni, 1998). Depending on its inﬂ uence on

the OTF, the same will also apply to I

M. So far, the structure of the

PSF has been determined by measuring the response of test objects,

such as ﬁ bers or ﬂ uorescent beads. However, it has been shown that

the relative phase can be extracted directly from the image data (Blanca

et al., 2002). This is of great importance in cases in which the imaged

object itself alters the relative phase of the interfering beams.

810 S.W. Hell and A. Schönle

A ﬁ lled OTF entails robustness in operation and lower amenability to

potential misalignment. Thus 4Pi microscopy allowed superresolved

imaging of specimens in aqueous media using water immersion lenses

(Bahlmann et al., 2001). This is noteworthy since water lenses feature

semiaperture angles of not more than 64° as compared to 68° available

for oil or glycerol immersion, therefore increasing side lobes and render-

ing the problem of missing frequencies in the OTF more severe. Imaging

a watery sample is one of the prerequisites of live-cell imaging.

For realistic aperture angles, the inherent lack of contiguity of the

OTF in the SWM renders the removal of interference ambiguities

impossible. The I

M becomes more viable through ﬁ lling the frequency

gaps present in the SWM, albeit with values that are weak with respect

to the zero-frequency components. Both systems have yet to prove their

applica bility to live cell imaging. In fact, recent investiga tions have cast

doubt on whether I

M is able to provide reliable data from live cells

with the available water immersion lenses. If water immersion lenses

of 70° and higher were available, the robustness and applicability of

M would signiﬁ cantly increase. Thus, this method would become

viable for a much larger variety of objects, at least for not too dense or

not too 3D-convoluted ones. The fact that the enlargement of the semia-

perture angle is the key to the performance of the I

M highlights the

exploitation of the entire spherical wavefronts as the central physical

element. In a sense, the I

M can be viewed as a 4Pi system that maxi-

mizes the degree of parallelization in the focal plane.

Parallelization is readily accomplished in 4Pi and 4Pi confocal

microscopy, as well. A multi focal variant of TPE 4Pi confocal micro-

scopy, termed multifocal multiphoton 4Pi microscopy (MMM-4Pi)

(Egnor et al., 2002), has indeed translated the typical 140 nm axial reso-

lution of a TPE 4Pi microscope into live cell imaging. Importantly,

although present and noticeable, phase changes induced by the cell

proved more benign than anticipated. Nevertheless, phase alterations

and wavefront aberrations due to refractive index changes within the

specimen are likely to conﬁ ne 4Pi microscopy and related techniques

to the imaging of individual cells or thin cell layers. In conjunction

with nonlinear image restoration this novel imaging method has dis-

played ∼100-nm 3D resolution under live cell conditions. For example,

MMM-4Pi microscopy has provided superior 3D images of the reticu-

lar network of GFP-labeled mitochondria in live budding yeast cells.

More recently, 4Pi microscopy has been realized in a compact optical

unit that was interlaced with a state-of-the-art single beam scanning

confocal ﬂ uorescence microscope (Leica TCS-SP2, Mannheim,

Germany). Operating in type C mode, i.e., coherent spherical wave-

fronts both for excitation and for confocal detection, this compact and

rugged system displayed a seven-fold improved axial resolution over

confocal microscopy in live cells (Gugel et al., 2004). This system is now

commercially available as the ﬁ rst far-ﬁ eld optical microscope with

axial superresolution.

The fact that single-photon excitation 4Pi confocal microscopy has not

been realized to date has been due to the superiority of the OTF in the

TPE version. Nevertheless, it is clear from imaging theory that a single-

photon 4Pi confocal microscope of type C features a more contiguous

Chapter 12 Nanoscale Resolution in Far-Field Fluorescence Microscopy 811

and better ﬁ lled OTF than an I

M, which inevitably operates in the

single-photon mode. Given further improvements in aberration com-

pensation and lens manufacturing, it is feasible that single-photon

excitation 4Pi microscopy (of type C) can also be realized in a reliable

manner. An inherent advantage of single-photon excitation over its

two-photon counterpart is that the much shorter excitation wavelengths

lead to axially narrower focal spots. For example, using a wavelength of

∼400 nm, a single-photon 4Pi microscope of type C would deliver an

axial resolution of ∼73 nm. This number further underscores the poten-

tial of 4Pi microscopy to deliver 3D images with axial sections well in

the tens of nanometer regime.

In summary, the resolution of a far-ﬁ eld ﬂ uorescence light micro-

scope can be improved down to the range of 60–100 nm along the optic

axis by coherently adding the focal light ﬁ elds of two opposing lenses.

The addition of the ﬁ elds leads to improved resolution for both excita-

tion at the focal point and detection of ﬂ uorescence at a common point.

The axial resolution is improved only if the main maximum of the

resulting PSF is at least twice as large as the primary side maxima

arising from the coherent addition. The latter condition can be fulﬁ lled

only if, at least for one of the processes, the added light ﬁ eld is a spherical

wavefront covering the aperture angle of the lens. This in turn shows

that the key physical element to improving the axial resolution by the

coherent use of two opposing lenses is not the production of an interfer-

ence pattern, but the enlargement of the aperture of the system.

4 Breaking the Diffraction Barrier

Increasing the total aperture of the focusing system with two opposing

lenses improves the 3D resolution of a far-ﬁ eld microscope, but does

not break the diffraction barrier. On the contrary, 4Pi microscopy

exploits the full potential of diffraction-limited imaging. This particu-

larly applies to (multiphoton) type C 4Pi confocal microscopy, which

can be regarded as the far-ﬁ eld optical microscope with the largest

possible aperture. For a microscope, being subject to the diffraction

limit implies that the system features the maximum resolution that

cannot be surmounted. On the other hand, breaking the diffraction

barrier implies the potential for featuring an inﬁ nitely sharp focal spot

or an OTF with an inﬁ nitely large bandwidth.

The ﬁ rst concept to break the diffraction barrier was STED ﬂ uores-

cence microscopy.

The physical concept of STED microscopy was

described as early as 1994 and was soon followed by GSD microscopy,

a related concept that also entailed diffraction-unlimited resolution

(Hell and Kroug, 1995). Whereas STED microscopy utilized stimulated

emission to deplete the excited state of the ﬂ uorophore, GSD aimed at

depleting its ground state by transiently pumping the dye into a long-

lived dark state, i.e., its triplet state. Importantly, both concepts share

the same principle for breaking Abbe’s barrier: a focal intensity distri-

bution featuring a zero point (or at least a strong gradient in space)

effects a saturated depletion of one of the molecular states that are essen-

tial to the ﬂ uorescence.

10,11

Following depletion, the state is populated

812 S.W. Hell and A. Schönle

again, that is, the saturated transition is reversible. A saturated transi-

tion, such as a depletion of a state, introduces vast nonlinearities that

eventually prove essential for breaking the diffraction barrier.

An even closer examination of the underlying concept shows that in

fact any saturable transition between two states where the molecule

can be returned to its initial state is a potential candidate for breaking

the diffraction barrier (Hell, 1997; Hell et al., 2003; Dyba and Hell, 2002).

The general concept has therefore been termed RESOLFT. The transi-

tion utilized can be selected to match the practical conditions of the

imaging problem at hand, such as the required intensities, the available

light sources, and the avoidance of photobleaching. An important

aspect with respect to biological applications is the compatibility with

live cells.

The basic idea of the RESOLFT concept can be understood by consid-

ering a molecule with two arbitrary states A and B between which the

molecule can be transferred. In ﬂ uorophores, typical examples for these

states are the ground and ﬁ rst excited electronic states and conforma-

tional and isomeric states. The transition A → B is induced by light, but

no restriction is made about the transition B → A. It may be spontaneous,

but may also be induced by light, heat, or any other mechanism. The only

further assumption is that at least one of the two states is critical to the

generation of the signal. In ﬂ uorescent microscopy this means that the

dye can ﬂ uoresce only (or much more intensively) in state A. Such a

system may be exploited to generate diffraction-unlimited resolution in

ﬂ uorescence imaging (or any kind or manipulation, probing, etc. that

depends on one of the states), which is illustrated in Figure 12–6.

We begin with all molecules or entities in the sample being in state A.

Our goal is to generate a diffraction-unlimited distribution of molecules

in state A. To this end, the sample is illuminated with light that drives

Figure 12–6. The RESOLFT principle. Diffraction-unlimited spatial resolution is achieved by saturat-

dye distribution of state A is illuminated by a strongly modulated intensity light distribution that

transfers the dye molecules to state B; ideally the modulation is perfect, so that the local intensity

A A

will also be limited by diffraction, because I(r) is diffraction limited and the relationship between I

and N

is basically linear. (b) Increasing the maximum intensity moves the points at which I(r) reaches

(r) drops to 0.5, the FWHM of N

(r) is correspondingly reduced. (c) Further increasing the maximum

read out as the desired signal stemming from a narrow region. To obtain an image, the local minima

are scanned across the sample. If the signal stems from state A, the intensity values N

(r) are read out

subsequently and the image is assembled in a computer. If the signal is generated by the “majority

population in state B” (e.g., state B is the ﬂ uorescent state) the function 1 − N

(r) is read out and the

image must be “inverted” later. This approach is challenged by signal-to-noise issues. (d) There is no

theoretical limit to this method and its resolution is ultimately determined by the available laser power

and the potentially limiting photodamage.

the transition from A to B. The intensity distribution I(r) of the illuminat-

The right-hand panel depicts the dependence of N (r) on the local intensity I(r), exhibiting the typical

I closer to the local intensity minimum, e.g., the zero. Because these are also the points at which

intensity beyond I leads to a further reduction of the FWHM. If A is the ﬂ uorescent state, N (r) is

left-hand panel shows I(r) and the resultant probability N (r) of the dye molecules being in state A.

B. (a) At I(r) < I , the modulation of the light is replicated in N (r). The narrowest distribution of N (r)

ing a linear but reversible optical transition from state A to state B. The simple explanation: A uniform

saturation behavior. I is deﬁ ned as the intensity at which half the molecules are transferred to state

minima actually are zeros. Here, we choose the narrowest possible modulation I(r) = cos (2πr/λ). The

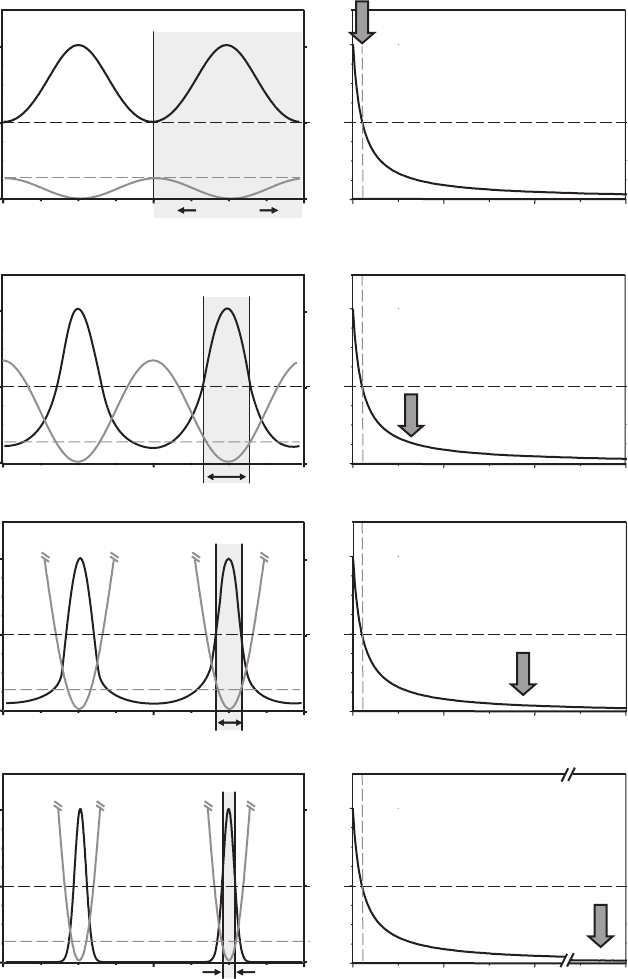
Chapter 12 Nanoscale Resolution in Far-Field Fluorescence Microscopy 813

ing light is of course diffraction limited but features one or several posi-

tions with zero intensity. After illumination, the probability, N

(r), of

ﬁ nding molecules in state A depends on I(r) and displays peaks where

I(r) is zero and no transitions to B are induced. If we choose the maximum

intensity I

max

in such a way that it is many times (ζ times, ζ = I

max

is called the saturation factor) higher than the saturation intensity, I

, of

the transition A → B (the threshold at which 50% of the molecules are

FWHM

r /

1.0

0.0

0.5

1.0

I [a.u.]

(r)

I(r)

FWHM

r /

1.0

0.0

0.5

1.0

I [a.u.]

(r)

I(r)

r /

1.0

0.0

0.5

1.0

I [a.u.]

FWHM

(r)

I(r)

r /

1.0

0.0

0.5

1.0

I [a.u.]

max

= I

sat

(r)

I(r)

I I

sat

max

= 5I

sat

max

= 15I

sat

max

= 40I

sat

(a)

(d)

(c)

(b)

FWHM

I I

sat

I I

sat

I I

sat

814 S.W. Hell and A. Schönle

transferred into state B), then molecules will be almost exclusively in

state B even at positions where I(r) is only a small fraction (∼5/ζ) of I

max

This means that while molecules remain in state A in the intensity zeros,

they are transferred to state B even at locations in the immediate vicinity

of the zero. Thus, the peaks of N

(r) become very narrow, featuring steep

edges at the same time. Figure 12–6 is presented in one dimension for

clarity, but this idea is readily extended to all directions in space and

hence to 3D imaging.

Their Fourier transform (the effective ex-citation OTF) of an increas-

ingly sharp peak correspondingly becomes wider with an in-creasing

max

. A complementary mathematical explanation for this fact is that

higher-order contributions that are described by several autoconvolu-

tions of the depletion pattern become more and more important for

higher intensities. This is in contrast to very low intensities where the

dependence of N

on the depletion intensity is approximately linear:

frequency space and the theoretical cutoff of the support can only be

pushed from the 4k we derived for conventional imaging to 6k. Thus,

the diffraction barrier is not truly broken for low intensities, but only

shifted to a slightly higher value.

The generated probability distribution can be used for high-resolution

imaging by applying scanning. Since the ﬂ uorescence stems exclusively

tion in the far ﬁ eld to be assembled. For particular conditions, the

resolution of this process is determined by the FWHM of the peaks in

FWHM can become inﬁ nitely narrow, that is down to the size of a single

acts as a condensor collecting the ﬂ uorescence. For example, when scan-

feasible if the nodes are further apart than the classical resolution limit

of the microscope. When the sharply localized ﬂ uorescence from the

nodes is imaged onto the camera, the resulting spot will certainly be

blurred as a result of diffraction, and possibly extend over several

pixels on the camera. However, if the nodes are further apart than

Abbe’ diffraction barrier, each of the blurred spots can be assigned to

the respective nodes. Sequential read-out of the camera makes it pos-

sible to integrate the measured signal of each blurred spot or line sepa-

rately and to associate it with the corresponding sharply localized

region in the sample from which the signal emerged.

in this case is simply the fact that in the RESOLFT concept the lens merely

molecule. The reason why Abbe’s spatial frequency cutoff does not apply

However, this does not imply that a RESOLFT microscope needs

to be based on single-beam scanning. Parallelization is readily

N (r), which in turn is solely determined by the saturation factor. The

to measure N (r). Sequential readout is absolutely mandatory in a far-

rescence signal allows an image with basically unlimited spatial resolu-

field optical system with a broken diffraction barrier, because—and Abbe

the zero(s) through the sample with simultaneous recording of the ﬂ uo-

was perfectly correct in this regard—the objective lens cannot transmit

from the immediate vicinity of the positions where I(r) is zero, scanning

possible and hence detection with a conventional camera is

the higher spatial frequencies through the lens (Hell, 2007).

ning with a single zero, the detector can be placed right next to the sample

N (r) = 1 − I(r)/I . Here, a single additional convolution is introduced in

Chapter 12 Nanoscale Resolution in Far-Field Fluorescence Microscopy 815

Importantly, implementing such a “wide-ﬁ eld” detection in a micro-

scope does not imply that subdiffraction resolution is possible in con-

ventional microscopy, since scanning is still an essential element in the

process of image formation. In a sense, “wide-ﬁ eld” is not the most

appropriate term in any event, since RESOLFT-based concepts always

imply that a part of the sample (at the very least, one single point) is

omitted from the saturable transition. Consequently, camera-based

RESOLFT approaches are essentially parallelized scanning concepts.

This scanning “wide-ﬁ eld” detection is readily explained in fre-

quency space as well. The PSF describing the generated probability of

the molecules of being in state A, N

(r), consists of periodic sharp

peaks, and can be described as a convolution of a single peak with a

comb function or with its multidimensional equivalent. In frequency

space, this is equivalent to a multi plication of the broad frequency band

of a single peak with a comb function. Thus the Fourier transform of

(r) which dominates the excitation OTF if given by delta-peaks sepa-

rated by the inverse distance of the nodes in I(r). The speed with which

they drop off towards large frequencies depends on the width of a

single peak in N

(r). The effective OTF is given by the convolution of

this series of delta-peaks with the detection OTF. Thus it will be con-

tinuous whenever the usable support of the latter is larger than the

distance between the delta peaks in the excitation OTF. Not surpris-

ingly, this just means that the intensity zeros of I(r) are far enough apart

so that the detection system can separate their ﬂ uorescence.

Note that complete depletion of A (or complete darkness of B) is not

required. It is sufﬁ cient that the nonnodal region features a constant,

notably lower probability to emit ﬂ uorescence, so that it can be distin-

guished from its sharp counterpart. Even if not A, but B is the brighter

state, it is p os sible to read out B and obtain the same superresolved image

after mathematical postprocessing that entails subtraction of signals

from each other. While reading out B, in principle, also delivers unlim-

ited resolution, this version is heavily challenged by signal-to-noise

issues. This stems from the fact that the “bright” light from the nonnodal

regions contributes with a substantial amount of photon shot noise.

It is also important to keep in mind that the nonlinearities intro-

duced in these concepts are not analogous to the nonlinear interactions

connected with m-photon excitation, mth harmonics generation, coher-

ent anti-Stokes–Raman scattering (Sheppard and Kompfner, 1978;

Shen, 1984), etc. In the latter cases, the nonlinear signal stems from the

simultaneous action of more than one photon at the sample, which would

work only at high focal intensities. In contrast, the nonlinearity brought

about by saturation and depletion stems from a change in the popula-

tion of the involved states, which is effected by a single-photon process,

namely stimulated emission. Therefore, unlike m-photon processes,

strong nonlinearities are achieved at comparatively low intensities.

Next, let us derive an estimate for the resolution achievable in such

a system at ﬁ nite depletion intensities (Hell, 2003, 2004). We denote the

rates of A → B and B → A with k

and k

, respectively. The time

evolution of the normalized populations of the two states n

and n

then given by

816 S.W. Hell and A. Schönle

/dt = −k

+ k

= −dn

/dt (20)

Independently from its initial state, after a time

t ≥ (k

+ k

)

−1

(21)

the equilibrium is approximately reached and the population of state

A is given by

= k

/(k

+ k

) (22)

During the process described in Figure 12–6, state A is depleted at a

rate k

= σI, where σ denotes the molecular cross section and the

intensity I is written as photon ﬂ ux per unit area. Hence, the equilib-

rium population is given by

(r) = k

/[σI(r) + k

] (23)

And N

= 1/2 for the saturation intensity

= k

/σ (24)

From Eq. (23) we see that where I(r) >> I

all molecules end up in B.

Thus, if we choose

I(r) = I

max

f(r) (25)

with I

max

>> I

, molecules in state A are found only in the nodes of the

diffraction-limited distribution function f(r). As an example, we choose

a sine-square intensity distribution, such as produced by a standing

wave

f(x) = sin

(2πnx/λ) (26)

for illumination, where n denotes the index of refraction of the medium.

A simple calculation shows that the FWHM of the peaks of N

and

hence the resolution of the microscope is then given by

∆x

=≅

πζ

arcsin( / )1

(27)

A saturation factor of ς = 1000 yields ∆x ≈ λ/100, but in principle the

spot of “A molecules” can be continuously squeezed by increasing ς.

Scanning with such a spot and simultaneous recording of the signal

from it deliver diffration-unlimited resolution. Equation (27) quantita-

tively describes this possibility in a microscope using diffraction-

limited beams.

If the intensity distribution I(r) is produced by a lens, the largest

frequency will be determined by the numerical aperture of the lens

n sin α, due to diffraction. In this case, Eq. (27) changes into

∆x

≅

παζsin

(27′)

If at the same time the molecules are being driven back from B to A

by a light intensity distribution following a cosine-square form, we

have k

= σ

max

of the transition. By deﬁ ning the saturation intensity as I

= σ

max

/σ,

we obtain

cos (2πn sinαx/λ), with σ denoting the cross section

Chapter 12 Nanoscale Resolution in Far-Field Fluorescence Microscopy 817

∆x

≅

π α ζsin 1

(27″)

This equation is particularly appealing, since for a vanishing satura-

tion factor ζ = 0 it almost assumes Ernst Abbe’s diffraction limited

form, whereas for ζ → ∞ the spot becomes inﬁ nitely small.

There are also adverse effects that need to be taken into account.

The ﬁ rst is that state A cannot be completely emptied by even very

intense illumination (e.g., because there is an excitation by the

same beam) and the second is that state B may also contribute to

the signal. Both can be considered by including a constant offset in

Eq. (23):

(r) = (1 − δ)k

/[σI(r)+ k

] + δ (28)

This would result in the image consisting of a superresolved image

plus a (weak) conventional image. The latter does not alter the fre-

quency content of the image. Therefore, given sufﬁ cient SNR, the reso-

lution will not deteriorate. In other words, if δ is sufﬁ ciently small so

as not to swamp the image with noise, the conventional contribution

can be subtracted (Hell and Kroug, 1995; Hell, 1997).

A further experimental problem is caused by imperfections of the

intensity zeros. Imagine the standing wave is aberrated and approxi-

mately described by

f(x) = (1 − γ) sin

(2 x/λ) + γ (29)

Such zeros with insufﬁ cient “depth” turn out to have a more serious

impact on performance. The maximum signal in the intensity minima

as above we obtain

∆x = +

(30)

At γ ∼ 1% resolutions of λ/20 at saturation factors of 100 can be achieved

without losing more than half the signal in the intensity minima.

presented above, it is also helpful to take a look at the frequency space

to relate these ﬁ ndings to the concepts and results presented in the

ﬁ rst part of this chapter. The dependence of the effective excitation PSF,

i.e., the distribution of the probability that a molecule actually emits a

value of N

(r) expressed in Eq. (23). If for I(r) = 0 the microscope

begins, for example, with a conventional PSF h

(r) used for imaging

the distribution N

(r) onto a camera, the effective PSF of the system is

given by

hr h r

Ir k

() ()

[()/]

1 σ

(31)

Now let σI

max

= ζ and I(r) = I

max

f(r) as above, then we can expand

(31) in a Taylor series

drops by a factor (1 + ζγ), as a result. Following the same calculation

While RESOLFT is far more intuitively explained in the way

nπ αsin

γ/

ﬂ uorescence photon, is governed by the saturation level-dependent

nπ αsin

and therefore the maximum achievable resolution is given by