Грушинский Н.П. Основы гравиметрии
Подождите немного. Документ загружается.


корение силы тяжести изменится на 1 м/с2, т. е. на 100 Гал.
Это очень большая величина. В практике применяется еди
ница в 1011 меньшая и равная Ы 0 _11с-2. Такая единица
называется этвеш.
§ 8. Нормальные значения вторых производных
потенциала притяжения
Пользуясь формулой (2.21), дающей закон нормального
распределения силы тяжести на эллипсоиде вращения, лег
ко построить формулы нормальных значений вторых про
изводных потенциала для того же эллипсоида, т. е. нор
мальные значения градиентов силы тяжести и кривизн.
Выберем горизонтальные подвижные прямоугольные коор
динаты с началом в рассматриваемой точке. Пусть ось х
направлена по касательной в меридиональной плоскости,
у — по касательной в плоскости первого вертикала и г —
по внешней нормали к поверхности.
Нормальные значения смешанной производной лег
ко находим, пользуясь формулой (2.39), из условия, что
в плоскости меридиана а —0; тогда и WNxy = 0.
Имея в виду, что для нормального эллипсоида имеет
место нормальное распределение силы тяжести, выражаемое
формулой (2.21), в которой g=у — нормальное значение
силы тяжести, получаем по формулам (2.35) и (2.36) нор
мальные значения вторых производных
*51=— И Г » - - - J-.
Отсюда по формуле (2.37)
I оризонтальные градиенты силы тяжести в направлениях
х и у получим как производные нормальной силы тяжести
по х и у из (2.21):
г -1 т ,М п 2 < р , П = з Н -
Наконец, нормальные значения вертикальной производ
ной Wzz легко получить, если вспомнить выражение
лапласиана для силы тяжести (2.3)
r » = 2 » - - r „ - r „ , = 2 < 0 4 - v ( i + l ) '
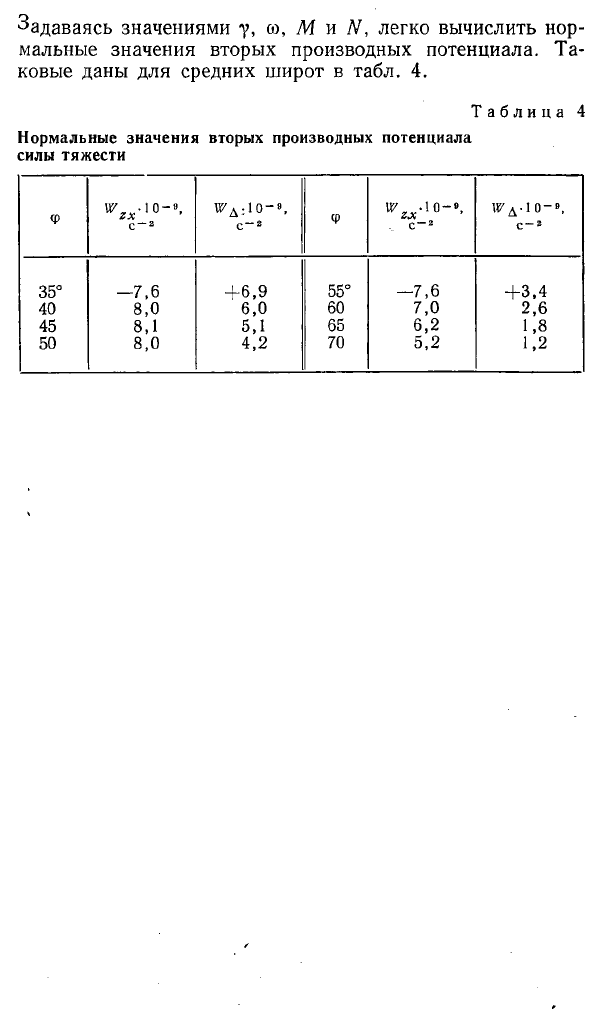
Задаваясь значениями у, св, М и N, легко вычислить нор
мальные значения вторых производных потенциала. Та
ковые даны для средних широт в табл. 4.
Таблица 4
Нормальные значения вторых производных потенциала
силы тяжести
ф
^ • 1 0 - .
с - 2
Ц7д;10-9,
с - 2
ф
.. С-2
w ь - 10-°.
с-г
35°
- 7 , 6 + 6 , 9 55°
- 7 ,6 + 3 ,4
40 8,0
6,0
60 7,0
2,6
45
8,1 5,1
65
6,2
1,8
50 8,0
4,2
70 5,2
1,2

Г Л А В A 3
О ГЕОМЕТРИЧЕСКИХ МЕТОДАХ ИЗУЧЕНИЯ
ФОРМЫ И РАЗМЕРОВ ЗЕМЛИ И ОПРЕДЕЛЕНИИ
ФУНДАМЕНТАЛЬНЫХ ПАРАМЕТРОВ ае, а
ИЗ ГРАДУСНЫХ ИЗМЕРЕНИЙ
§ 1. Взаимосвязь гравиметрии с геодезией
Геодезия — наука об измерении Земли. Она столь же
древнего происхождения, как астрономия, математика и
физика, и в эпоху своего зарождения была неотделима
от них. Возникнув из практических потребностей людей,
она и до сих пор несет службу обеспечения этих потребно
стей в картах, определении расстояний и координат точек
на земной поверхности, обеспечения мореплавания, воз
духоплавания и определения положений искусственных
небесных тел, строительства и многих других отраслей
практической деятельности человека.
Геодезию можно определить как науку об измерении
Земли и ее внешнего гравитационного поля. Из геодезии
выделилась высшая геодезия, задачей которой является
определение положения сети опорных точек в единой
системе пространственных координат и, в конечном счете,
определение формы и размеров Земли в основном геомет
рическим методом, и теория фигуры Земли, или физиче
ская геодезия, изучающая фигуру и внешнее гравитацион
ное поле Земли по величинам напряженности поля силы
тяжести.
Поскольку свойства гравитационного поля Земли не
отделимы от ее геометрических характеристик, последнее
время начали выделять теоретическую геодезию как науку
о фигуре и внешнем гравитационном поле Земли и их
изменениях во времени, объединяя таким образом теоре
тическую часть высшей геодезии и теорию фигуры Земли.
Разделы высшей геодезии, теории фигуры Земли и небесной
механики, в которых описываются движение и методы на
блюдений искусственных небесных тел для решения гео
дезических задач, выделились в спутниковую, или косми
ческую геодезию.
^Другие составные части геодезии — это топография (из
мерение небольших участков Земли, когда их можно при

нять за плоскость), картография, геодезическая астроно
мия, аэрофотосъемка и фотограмметрия.
Из сказанного видно, как тесно переплетаются грави
метрия и геометрические методы в геодезии, гравиметрия
и спутниковая геодезия. Недаром основная научная задача
высшей геодезии формулируется сейчас как определение
фигуры и внешнего гравитационного поля Земли. Именно
поэтому, рассматривая в нашем курсе основные положения
современной гравиметрии, мы не можем обойтись без
объяснения некоторых геодезических понятий.
§ 2. Земной эллипсоид. Система координат
Земля имеет сложную и неправильную поверхность с
впадинами и возвышенностями, горами и долинами. .Эта
поверхность не может быть представлена простыми мате
матическими формулами, для нее сложно устанавливать
какие-либо соотношения, например, между координатами
соседних пунктов и расстояниями между ними. В качестве
поверхности, представляющей Землю, принимается обычно
эллипсоид вращения, подобранный и ориентированный в
теле Земли таким образом, чтобы он ближе всего соответ
ствовал поверхности геоида. Такой эллипсоид называется
общим земным эллипсоидом и характеризуется минимумом
суммы квадратов отклонений от геоида:
"У £2 = min.
Это условие однозначно определяет размеры эллипсоида
и его ориентирование в теле Земли. Однако для построения
такого эллипсоида нужно, чтобы вся Земля была подробно
измерена геодезически. Для практической работы подби
рается некоторый промежуточный эллипсоид, построенный
и ориентированный по ограниченной области, например,
для одной или ряда стран. Такой рабочий эллипсоид назы
вается референц-эллипсоидом, или эллипсоидом относи
мости. Он является той поверхностью, на которую должны
быть спроектированы все длины и направления, измерен
ные- на физической поверхности Земли. В разных странах
применяются’"- различные референц-эллипсоиды. Поэтому
и геодезические системы разных стран не представляют
единой общеземной геодезической системы.
В Советском Союзе в качестве референц-эллипсоида
принят эллипсоид Ф. Н. Красовского. Этот эллипсоид
выведен по геодезическим измерениям на территориях
Советского Союза, Западной Европы и Северной Америки.

0^ = 6 378 245 м — большая полуось,
а — 1:298,3 — сжатие.
Он ориентирован по Пулкову, в котором заданы начальные
координаты и азимуты — так называемые исходные геоде
зические даты, которые получили название «Система
1942».
В высшей геодезии применяются две основные системы
координат: декартова геоцентрическая X, Y, Z (рис. 10)
и сферические коорди- тора — и положение точки наэллипсо-
наты- иде определяется двумя криволиней
ными координатами: широтой В и дол
готой L. Широта В определяется как угол, образуемый
нормалью к эллипсоиду в рассматриваемой точке и пло
скостью экватора, и отсчитывается от плоскости экватора
до 90° к северу и к югу. Долгота L есть угол между пло
скостями нулевого мер иди ал? и меридиана, проходящего
через данную точку. Долирта отсчитывается от нулевого
меридиана, обычно гринвичского, от 0 до 180° к западу и к
востоку. Эти координаты обычно называются геодезиче
скими. Следует отличать их от координат астрономиче
ских — широты ф и долготы X. Отличие связано с тем, что
геодезические координаты, заданные на эллипсоиде вра
щения, определяются положением нормали к эллипсоиду,
тогда как астрономические определяютсяУ'сУпомощью ин
струмента, установленного по отвесу, т.Ре. по нормали к
уровенной поверхности, проходящей через точку наблю
дения. Для определения точек на физической!поверхности
Земли вводится третья координата — Я, отсчитываемая
от референц-эллипсоида по нормали. Кроме геодезических
и астрономических координат, часто употребляются такие,
в которых долгота совпадает с долготой геодезической,
а широта определяется углом Ф радиуса-вектора с пло
2
с началом в центре референц-эллип-
соида, осью абсцисс, лежащей в плос
кости нулевого меридиана, и осью z,
совпадающей с полярной осью Земли,
и ортогональная криволинейная си-
Y стема координат В, L, связанная с
нормалью к отсчетной поверхности
референц-эллипсоида.
Представив Землю таким эллипсо-

скостью экватора. Часто также используется приведенная
широта и, образуемая углом между плоскостью экватора
и радиусом ае сферы, построенной на экваториальном
сечении эллипсоида. Этот радиус должен проходить через
точку М' пересечения этой сферы ординатой точки М на
эллипсоиде (рис. 11).
г' ,
---
----------
_м'/
Рис. 11. Приведенная ши
рота и и геоцентрическая у
широта Ф. *
Для эллипсоида вращения, в силу долготной£симмет-
рии, формулы преобразования координат для плоского
случая легко распространяются на случай пространствен
ный. Поэтому широко применяется система плоских пря
моугольных координат х, у, причем положение плоскости
задается долготой L.
§ 3. Преобразования координат
1. Выражение прямоугольных коор
динат меридианного эллипса ч ер е з ш и
роту и долготу.
* Рис. 12. Пояснение к формулам преобразования геодезических коор
динат.
Точка М эллипса (рис. 12) с координатами х, у или р, В
удовлетворяет уравнению эллипса
X2 . U2 1 /0 1ч

где а и b — большая и малая полуоси соответственно. Диф
ференцируя это уравнение по х как неявную функцию,
получаем
£ + £ ! = О, (3.2 )
но, как видно из рис. 12,
g = tg (9 0 ° + B) = -c tg fi. (3.3)
Вводя значение производной в (3.2), получим
JL-JLctgB=Q
и
62 ♦ с
Поскольку •
&2= а 2( 1—е2),
где е — эксцентриситет эллипса,
y= x(l—e2)tg В. (3.4)
Из уравнений (3.1) и (3.4) найдем выражение для х и у
х2 х2 (1— e*)atg2 В
__
j
через широту
Х‘ . X*
а2 "• а2(1—еа)
или, вынося х2 за скобку и перенося в левую часть,
л а2 a2 cos2 В
Х ~ l + t g 2B — e2tg2B ~ 1— easin2В '
Извлекая корень квадратный и внося значение х в
(3.4), получим
a cos В
х ■
У‘
V 1 — е2 sin2 В ’
q ( l— e2)sinB
|^1 — е2 sin2 В ,
(3.5)
2. Выражение геодезической широты
В через геоцентрическую Ф.
Геометрически очевидно (рис. 11), что tg (j)_ JL Ис
пользуя (3.5), получаем х
tg Ф = (1 — «2) tg 5 = ^ tgВ (3>6)
или tg В—tg Ф = e2tg В.
56

Пользуясь формулой для разности тангенсов, получим
sin (В — Ф )
__
sin В
cos Ф cos В cos В
и
sin (В — Ф) = е2 sin В cos Ф « еа sin 2В. (3.7)
Разность (В—Ф) достигает максимума при В=45° и равна
тогда 11',8.
3. Выражение приведенной широты и
через геодезическую В.
Геометрически очевидно (рис. 11), что
х=а cos и
и
RM'=a sin и.
В то же время по теореме Пифагора
x2+RM '2= a\ (3.8)
а из уравнения эллипса
х* + а^ У * = а \
а»
Сравнивая два последних равенства, получаем
RM’ = ^ y .
Используя формулы (3.10), (3.8) и (3.4), получаем
a sin и = a cos и (1 — еа) tg В,
откуда
tg« = f (\-e*)tgB = U g B. (3.11)
Полученные в этом параграфе соотношения позволяют
найти выражения для таких важных в геодезии величин,
как радиусы сечений в плоскостях меридиана и первого
вертикала, а также длины дуг меридиана и параллели.
§4. Нормальные сечения, главные радиусы кривизны
Сечения поверхности плоскостями, проходящими через
нормаль к ней в какой-либо точке, называются нормаль
ными сечениями в данной точке. Кривая, образованная
пересечением плоскости’”нормального сечения с поверх
ностью, тоже называется нормальным сечением. Из бес
(3.9)
(3.10)

численного множества таких нормальных сечений можно
выделить экстремальные (с максимальным и минимальным
радиусами кривизны) — они называются главными нор
мальными сечениями. В дифференциальной геометрии вы
водится формула Эйлера, связывающая кривизну произ
вольного нормального сечения с кривизнами главных
сечений, плоскости которых взаимно перпендикулярны:
1 cos2 Л , sin2 Л /0 , оч
A T '
Здесь М — радиус кривизны меридианного сечения, N —
радиус кривизны сечения первого вертикала, А — азимут
сечения, отсчитываемый от направления на север.
Радиус кривизны R меридианного сечения найдем по
формуле дифференциальной геометрии для плоской кривой
R = {- 1-± Уу У / !. (3.13)
Для меридианного сечения
(3.14)
* _ 1 dB
У sin2 В dx'
dB
Значение найдем из (3.5):
dB — (1 — е2 sin2 5)*/*
dx а(1 — е2) sin В
Тогда
# = М =
-----
а(1~ е2)
(1—e2sin2 В) ,2‘
Радиус кривизны сечения плоскостью первого вертикала
получим из условия, что радиус кривизны наклонного
сечения равняется радиусу кривизны нормального сечения,
умноженному на косинус угла между этими сечениями (так
называемая теорема Менье). В качестве наклонного се
чения выберем сечение параллелью. Радиус кривизны
такого сечения будет
г = x = N cos В,
Вводя х из (3.5), получаем
a cos В , г D
г = х — — = N cos В,
у 1 — е2 sin2 В
N = г а = . (3.15)
1^1 —е2 sin2 В

Зная радиусы меридиана и первого вертикала, легко
вычислить соответствующие длины дуг (см. следующий
параграф).
§ 5. Длина дуги меридиана и параллели
Длина дуги меридиана sM, заключенная между точками
с широтами Ву и В2, может быть получена в результате
интегрирования выражения для элементарной дуги ме
ридиана ds=M dB в пределах от Вх до В 2:
в ,
sM = М dB.
ih
Вводя сюда М из (3.14), развертывая знаменатель в ряд
и интегрируя почленно, получим удобное выражение для
вычисления длины дуги меридиана:
sM = f — Цу- dB =
M J (1 —e3 sin2 B)
д ,v ’
в г
= a( 1 — e2) J ^1 -f e2sin25 + у e4sin4В 4-
Bi
-f-e6 sin6 В + ...jd B .
Выразим sin2 В и sin4 В через косинусы кратных двойных
углов:
sin2B = y — у cos 2В,
sin4B = -|-— у cos 2В + у cos 4В;
тогда получим простую формулу в виде интеграла ряда,
который легко написать для любого числа членов:
В ,
sM = a(l — е2) J (Лх — Аг cos 2В + А3 cos 4B~|-...)dB,
Вг
■ где
Ч 4.4
Л1= 1 + -|- е2 + е4 + .. . = 1 ,0050517739,
А2 = 1 е2 + е4 + . .. = 0,00506237764,
А3 = ||е 4+ - =0,00001062451,
