Грушинский Н.П. Основы гравиметрии

Подождите немного. Документ загружается.

верхностях, по определению, отсутствуют тангенциальные

составляющие сил, и массы, расположенные на них, нахо

дятся в состоянии устойчивого равновесия, в частности, не

происходит перетекания жидкости. Уравнение семейства

уровенных поверхностей получим приравниванием потен

циала константе:

V = C.

Это семейство обладает тем свойством, что изменение по

тенциала V при перемещении dS по поверхности равно О,

§ = Fcos(F, 5) = 0, (1.23)

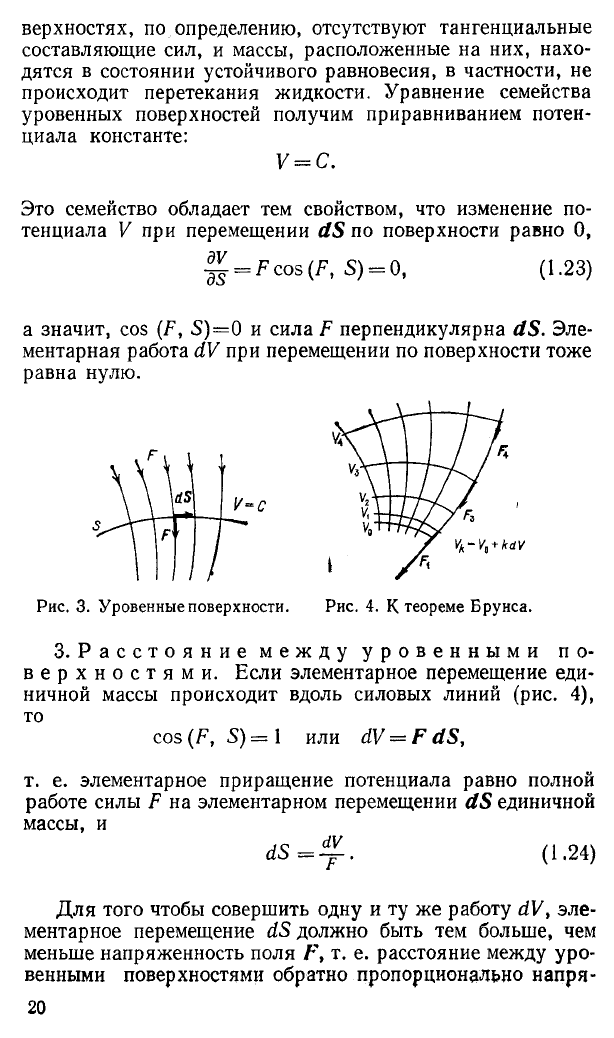
а значит, cos (F, S )= 0 и сила F перпендикулярна dS. Эле

ментарная работа dV при перемещении по поверхности тоже

равна нулю.

3. Расстояние между уровенными по

верхностями. Если элементарное перемещение еди

ничной массы происходит вдоль силовых линий (рис. 4),

то

cos (F, S) = 1 или dV = F dS,

т. е. элементарное приращение потенциала равно полной

работе силы F на элементарном перемещении dS единичной

массы, и

d S = ^ . (1.24)

Для того чтобы совершить одну и ту же работу dV, эле

ментарное перемещение dS должно быть тем больше, чем

меньше напряженность поля F, т. е. расстояние между уро

венными поверхностями обратно пропорционально напря

женности поля. Это положение носит название теоремы

Брунса.

Из этого свойства вытекает также теорема о том, что

уровенные поверхности никогда не пересекаются и не со

прикасаются друг с другом. В самом деле, совпадение та

ких поверхностей в одной точке неизбежно приводит к их

полному совпадению.

4. Объемный потенциал и потенциал

простого слоя. В выражении для потенциала (1.16)

элемент массы можно представить как

dm=odx,

где dr — элемент объема, а — объемная плотность рас

пределения масс по объему т, причем

6т

а = lim -F-

бт-*0 0Т

— величина конечная. Тогда получим объемный потенциал

(1.25)

Рассмотрим далее случай, когда притягивающие массы

сосредоточены на поверхности s в виде слоя малой толщины

h. Если ds — элемент поверхности, то элемент объема dx

можно представить как

dr=hds.

Тогда объемный интеграл приобретет вид

V = G^ — .

Переходя к пределу при условии lim ah — o', получаем по-

h->- о

тенциал простого слоя

а ~(Г’ (i,26)

где а — поверхностная плотность распределения масс на

поверхности, s — величина конечная.

5. Потенциал шара на внешнюю т о ч -

к у. Во многих задачах гравиметрии, тем более астроно

мии, приходится иметь дело с телами сферической или

близкой к сферической формы. Поэтому представляет ин

терес рассмотреть потенциал таких тел.

Потенциал материального шара на внешнюю точку по

лучим интегрированием по радиусу потенциала простого сфе

рического слоя, который, в свою очередь, получается ин

тегрированием потенциала по сферической поверхности.

Представляя элемент поверхности в сферических коор

динатах R, if), %

где ij) — полярное расстояние, Я — долгота, находим

Полагая поверхностную плотность постоянной, вынесем а'

за знак интеграла и, интегрируя это выражение по долготе,

получим

Подынтегральное выражение преобразуем с помощью ра

венства (см. рис. 5) pa= t f8+ r 2—2i?rcoso|). Дифференцируя

левую и правую часть последнего, получим

Отсюда непосредственно получается подынтегральное вы

ражение в виде

Подставляя его в формулу (1.27) и заменяя пределы ин

тегрирования, имеем

Пределы интегрирования определяются положением са

мой близкой и самой далекой от А точками поверхности,

соответственно точками В и В’ (рис. 5). Вынося за знак

интеграла постоянную величину — и интегрируя, получим

ds=R2 sin'll? dty dk,

о о

(1.27)

р dp = Rr sin \|) dty.

У = 2ква' J ^-dp.

r + H

С R

(1.28)

r-R

Последняя формула показывает, что потенциал притя

жения бесконечно тонкого сферического слоя на внешнюю

точку равен потенциалу притяжения центра сферы со скон

денсированной в нем всей массой сферического слоя.

Чтобы получить потенциал слоя конечной толщины и

всей сферы, надо выражение (1.29) проинтегрировать по ра

диусу от R до некоторого Ri<.R (рис. 6). Заменив в подын

тегральном выражении поверхностную плотность а' через

объемную плотность а,

Знак минус взят, поскольку интегрирование ведется внутрь

сферы.

Выполняя интегрирование при постоянной плотности а,

получим для сферического слоя

сферического слоя, можно объединить формулы (1.30) и

йт(£,,т]Х) , dm ((5,,7]Х)

в’

Рис. 5. Потенциал шара на внеш

нюю точку.

Рис. 6. Потенциал шара на внут

реннюю точку.

o'=odR,

приходим к выражению

(1.30)

и для полной сферы (/?i=0)

(1.31) , записав

V — G —

где М — масса однородного сферического слоя или целого

однородного шара.

Таким образом доказана теорема, что однородный сфе

рический слой так же, как и однородный шар, развивают

потенциал, равный потенциалу точки, расположенной в

центре шара и содержащей всю массу шара.

6. Потенциал шара на внутреннюю

точку. Формула (1.28) позволяет найти потенциал бес

конечно тонкого внутреннего шарового слоя поверхност

ной плотности а'. Для этого в ней надо только заменить

пределы и интегировать по радиусу от самой близкой к А

точки поверхности В, где p=R—г, до самой далекой В',

где р=R+r,

R + r R+r

V^2nGa' j ~-dp = 2nGo' y - j dp = 4nGo’R. (1.32)

R-r R-r

Чтобы распространить эту формулу на слой конечной тол

щины, нужно ввести объемную плотность ог = ^ и про

интегрировать в пределах от г до R:

1/=4jxG<j$ RdR = 2nGo(R*-R\). (1.33)

Потенциал полной сферы на внутреннюю точку А сла

гается из потенциала внешнего по отношению к точке сфе

рического слоя, задаваемого формулой (1.33) при Ri=r,

и потенциала, внутреннего по отношению к точке шара ра

диуса г, задаваемого формулой (1.31). Итак, при R > r

У = ^внухр + Квнешн = 2яСа ( R* - г2 + 4 г1•) =

= -|nG a(3tf2- r 2). (1.34)

. i

7. Притяжение шаровых тел. Чтобы по

лучить силу притяжения сферическим слоем и полной сфе

рой внешней и внутренней точек, нужно продифференци

ровать соответствующие значения потенциала по направле

нию г. Приводим все эти значения в табл. 2.

Таблица 2

Потенциал и сила притяжения сферических тел

Притягивающ ее

тело

Потенциал

Фор

мула

Величина силы

Для внешней точки

Бесконечно

тонкий шаро

вой слой

, R2

V = 4jiG o —

(1 .29 ) „ — 4nGo'R2

F ~

Шаровой слой

конечной тол

щины

(1 .30 )

4 R3- R \

F - 3 ,Ga r2

Шар

V = ~ G — R3

о Г

Для внутренней

(1.31)

точки

f = - ± g ^ r *

Бесконечно V = 4 nGo’R (1.32)

тонкий шаро

вой слой

Шаровой слой

конечной тол

V = 2 nGo(R2- R \)

(1.33)

F = 0

щины

Шар

K = -|-nGo (3R2 — r2)

(1.34)

F= — nGor

Заметим, что 4я R2a' есть масса бесконечно тонкого ша-

рового слоя, у яа (R3 — Rf) — масса шарового слоя конечной

толщины, а у nRsa — масса шара. Поэтому все формулы для

внешней точки приводятся к виду: для потенциала V—

— G— и для силы F — — G-s-.

г г

8. Уравнение Лапласа. Потенциал притяже

ния во внешнем пространстве удовлетворяет уравнению

Лапласа

ДУ = 0, (1.35)

д2 д2 дг

где А = ^ 5 + -щр + -^5 — оператор Лапласа. Докажем это

свойство на примере однородного шара. Продифференци

ровав выражение для потенциала однородного шара

V = G —

дважды по координатам х, у, z с учетом (1.17) и (1.18), по

лучим

1 3 ( * - |) 21&V

дх2

dif

d z 2

-Gm у

-Gm

3 (у— T))3

u~v ^

— =:

---От

3 (* - 0 2'

Складывая все три вторые производные, убеждаемся в ска

занном:

A V = —Gm { £ - Д [ ( * - £ ) Ж * / - л ) а + ( г -£ ) 2] } ^ о .

Уравнение Лапласа инвариантно относительно системы ко

ординат и распределения плотности; иными словами, оно

справедливо в любой ортогональной системе координат при

любом распределении масс и любой

форме тела.

9. Уравнение Пуассона.

Потенциал притяжения в точках внут

ри масс удовлетворяет уравнению Пу

ассона

Д У =—4nGa.

Рис. 7. К теореме Пу

ассона.

Для доказательства этого предло

жения нужно массы, внутри которых

находится точка А, разделить на две

части, обнеся точку А сферой малого радиуса/? (рис. 7). То

гда для всех масс вне сферы радиуса R точка А будет внеш

ней и потенциал Vly развиваемый этими массами, будет

удовлетворять уравнению Лапласа

АУ!=0.

Для сферы радиуса R точка А будет внутренней, и в

ней массы, заключенные внутри сферы, согласно формуле

(1.34) будут развивать потенциал

Уа = 4 л0сг (ЗЯ2- г 2).

Применив оператор Лапласа к этому выражению, получим

d2V , , а2К, , d2Vo

AV.

дх2

ду2

d z 2

у nGo — у kGo — у яС а.

Значит, для точки внутри масс

АУ = АУ1-[АУ2 =

-inGa. (1.36)

Уравнение Пуассона также инвариантно относительно сис

темы координат и распределения масс.

§ 4. Разложение потенциала в ряд

Разложим в ряд Маклорена

и (г) — и (0) + тт и ' (0) + -кг и " (0) + . . .

(1.37)

подынтегральную функцию — в выражении для потенциала

(1.16). Напомним, что p = Jf К*-\-гг— 2Rrcosip.

Для простоты положим, что мы имеем дело со сферой

единичного радиуса R — 1. Тогда

, \ 1 1

и(г) = — = г .

Р / 1 + г 2—2/-cosij)

Дифференцируя функцию и (г) и подставляя значение г=

= 0 , получим коэффициенты разложения (1.37)

и (0) = 1,

и'(0)=

и"(0):

и'"( 0):

Л —-COS

(1 + r2- - 2r cosi|))3/a

3 (r—cos г|;)2 1

рэ P > = o

15 (r — cos i|;)3J , 9 (r—cos if)

= COS г|з,

г-о

= 3 cos2 — 1,

= 3 (5 cos 3\|j—3 cosij?)

и т. д. Тогда разложение (1.37) принимает вид

/ \ 1 1 , , , о 3 cos2 Ф — 1 .

u(r) = — = l + rcos*j3 + г2

------

f -------f- (1.38)

Коэффициенты при степенях г — это так называемые поли

номы Лежандра, обозначаемые обычно через Pt (coso|)). Вво

дя эти обозначения в (1.38), получим

и [г) = Р0 (cos г])) + rPx (cos i|)) + r2P 2 (cos \Jj) -f . . .

•• • = 2 r»pn (co sy). (1.3 9 )

n = 0

Для сферы произвольного радиуса R=a, аф\ функ-

дию — можно записать так:

Внеся это выражение в формулу (1.16) для потенциала, по

лучим

Это представление потенциала в виде бесконечного ряда

полиномов Лежандра.

Раскрывая сумму в (1.41) и удерживая три первых чле

на, получим выражение потенциала в виде суммы трех ин

тегралов

__ q j J cos ^ dm _j_ q _£L_ J (3cos2ij3— 1) dm-\- . ..

M M M

(1.42)

Рассмотрим все интегралы отдельно.

Первый интеграл представляет собой потенциал сфери

ческой Земли:

обращается в нуль при выборе начала координат в центре

масс. В самом деле,

или

(1.40)

(1.41)

М п = О

Второй интеграл

. дг| + г/г)4-г£

cos гЬ = —-

т га

где значения л;, у, г, £, т], Z, очевидны из рис. 5, и тогда

J a cos dm = х J ldm + у^ т]dm + z ^ t,dm.

М М М М

Интегралы в правой части равенства — координаты центра

масс, которые должны обращаться в нуль согласно нашему

выбору начала координат.

Третий интеграл содержит вторую зональную гармони

ку. Раскроем в нем значение cos -ф:

J a2 (3cos21|)— 1 )dm =

= G2М [ ^ ( x^ + yr\ + z0 2 — ^2] dm =

— [(3x2g2 + 3«/2ri2 + 3z2£2) —a2/-2]dm =

— [3x2g2 + 3i/2r|2 + Зг2£2 — а2 (x2 + у2 -f г2)] dm. (1.43)

Здесь опущены произведения вида J xy\x\dm = xy J dm,

M M

которые являются произведениями моментов инерции и об

ращаются в нуль в случае выбора координатных осей со

впадающими с главными осями инерции.

Внося в подынтегральное выражение а2= | 2-Hri2+ £ 2 и

группируя члены с х2, у2 и z2, запишем третий интеграл

в виде

G2?

G2f>

Гх

J л:2(3|2 —a2)dm + Jz/2(3r|2 — a2)dm + Jz2(3£2—a2)dm

2J (2ga — г)2— t,2)dm + y2J (2r]2— £2 — g2)dm +

м м

+ z ^ { 2 i 2- l 2- 42)dm .

Если обозначить моменты инерции тела относительно осей

х, у, z

S (г|2 + £2) dm = A, J а 2 + £2) dm = В,

м м

^ (Е2 + 112)dm = C,