Грушинский Н.П. Основы гравиметрии

Подождите немного. Документ загружается.

При небольших расстояниях и малых высотах можно поль

зоваться этим методом и этой формулой. Однако на больших

расстояниях появляются ошибки, возникающие из-за не

параллельное™ уровенных поверхностей.

Если за элементарные превышения dh взять последова

тельно превышения изображенных на рис. 17 поверхно

стей, то легко видеть, что их сумма от Л до В зависит от

избранного пути:

2 Ак1Ф ^Ы г1Ф 2

АА'В АВ АВ’В

Значит, сделанное нами определение высот неточно. Чтобы

освободиться от возникающей ошибки, высоты определяют

через потенциал. Приращение потенциала, как известно,

не зависит от пути, а является функцией точек. Измене

ние потенциала от одной уровенной поверхности к соседней

gdh —■ величина постоянная, не зависящая от того, к

какой точке поверхности она отнесена. Очевидно,

2 = S giAb

АА'В АВ АВ'В

По теореме о среднем

2 gi Afcj = S gi Ahi = gcP 2 ДА/ = g cvH-

AB AB'B B'B

Высоту определяют делением суммы элементарных прира

щений потенциала на среднее значение g на отрезке ВВ'

8с р АВ

или в интегральной форме

(3.24)

Ср АВ

Так определенная высота называется ортометрической

высотой и обозначается Я ор. Для ее вычисления нужно,

помимо превышений Ahit измерить ускорение силы тяжести

gi вдоль профиля нивелирования и знать gcp — среднее

значение по самой высоте, т. е. по линии ВВ' (рис. 17.).

Величину строго говоря, мы не знаем, поэтому вместо

geP обычно вводится 7 ср — среднее нормальное значение

силы тяжести по линии ВВ'. Высота, определенная через

нормальный потенциал, называется нормальной высотой

я . = 7 - <3-25>

YcP АВ

или в интегральной форме

АВ

Нормальные высоты легко вычислить, и именно ими обычно

и пользуются при всех геодезических работах. Отличие

нормальных высот от ортометрических не превосходит на

равнине нескольких сантиметров.

В В В Я В Физ.поаЗемли

У г ^

—77777

В".

\ш/)7тт

Квазигеоид

’

-------

-------------- S '

Геоид =*

= ср. jpi океана

Ь' -у . Эллипсоид

ОТНОСИМОСТИ

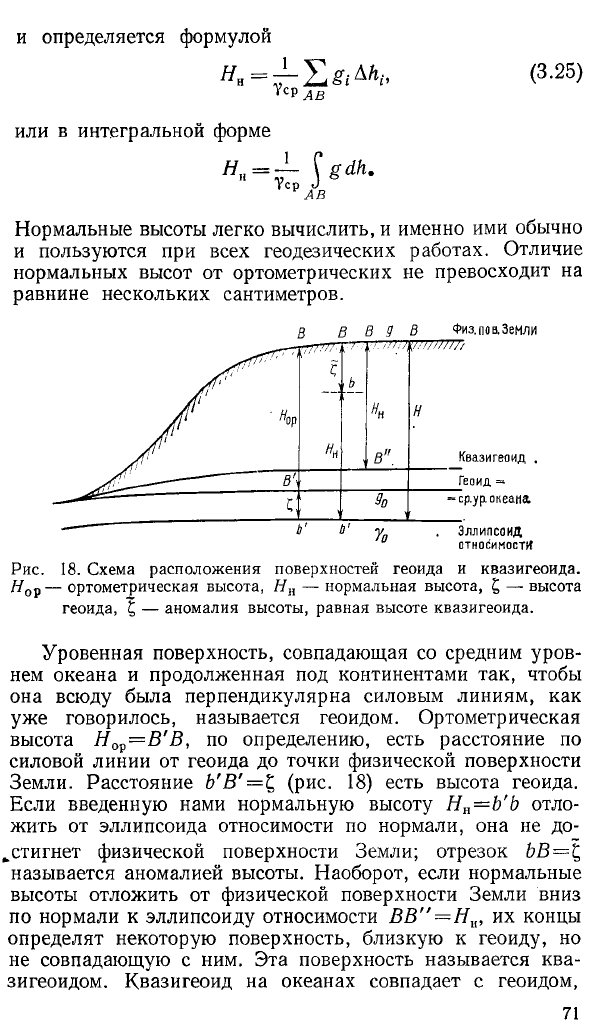
Рис. 18. Схема расположения поверхностей геоида и квазигеоида.

Нор — ортометрическая высота, Ня — нормальная высота, £ — высота

геоида, £ — аномалия высоты, равная высоте квазигеоида.

Уровенная поверхность, совпадающая со средним уров

нем океана и продолженная под континентами так, чтобы

она всюду была перпендикулярна силовым линиям, как

уже говорилось, называется геоидом. Ортометрическая

высота Я 0р= В '5 , по определению, есть расстояние по

силовой линии от геоида до точки физической поверхности

Земли. Расстояние b'В'= £ (рис. 18) есть высота геоида.

Если введенную нами нормальную высоту Нн=Ь'Ь отло

жить от эллипсоида относимости по нормали, она не до

стигнет физической поверхности Земли; отрезок ЪВ=\

называется аномалией высоты. Наоборот, если нормальные

высоты отложить от физической поверхности Земли вниз

по нормали к эллипсоиду относимости ВВ"=Н1{, их концы

определят некоторую поверхность, близкую к геоиду, но

не совпадающую с ним. Эта поверхность называется ква

зигеоидом. Квазигеоид на океанах совпадает с геоидом,

а на суше (в равнинных областях) отличается от него на

несколько сантиметров; в горной области при высотах

порядка 5000 м и значительных аномалиях расхождения

геоида и квазигеоида могут достичь двух метров. Практи

чески мы никогда не получаем ортометрических высот и

всегда имеем дело с высотами нормальными и аномалиями

высот, т. е. с квазигеоидом. Поэтому далее всегда, говоря

о геоиде, будем подразумевать квазигеоид.

Понятия нормальной высоты и квазигеоида, являющиеся

сейчас фундаментальными понятиями высшей геодезии

и гравиметрии, ввел в сороковых годах советский ученый

М. С. Молоденский как составную часть созданной им стро

гой теории определения фигуры Земли и ее внешнего гра

витационного поля по измерениям на ее физической по

верхности.

Расхождение между геоидом и квазигеоидом легко вы

числить. Оно совпадает с разностью нормальной и орто-

метрической высот:

Это выражение можно представить в виде

6 :gcpZZ7cp

gcp "

Разности gcp—Yep могут достигать нескольких сотен мил-

лигал. Приняв эту "разность равной 100 мГал, получим для

средних высот порядка 500 м 8£=5 см.

Г Л А В A 4

РЕДУКЦИИ СИЛЫ ТЯЖЕСТИ И ОБРАЗОВАНИЕ

АНОМАЛИЙ

§ 1. Понятие аномалий. Смысл введения редукций

При изучении гравитационного поля его удобно раз

делить на правильную часть, так называемую нормальную,

и аномальную. Составляющая, зависящая от высоты, учи

тывается по вертикальному градиенту. Отклонение наблю

денного значения ускорения силы тяжести в данной точке

от вычисленного по формуле нормального значения силы

тяжести называется аномалией силы тяжести. Аномалия

определяется как разность

A g=g—y- (4.1)

В отличие от сильно изменяющихся значений g аномалии

изменяются на земной поверхности всего на несколько

сотен миллигал. Если значения g и у в этой формуле за

даны для одной и той же точки, аномалия называется

чистой. Однако обычно нормальное значение ускорения

силы тяжести у задается нормальной формулой на поверх

ности эллипсоида относимости, соответствующего нор

мальному распределению силы тяжести, тогда как g опре

деляется в точках физической поверхности Земли. Значит,

для того чтобы вычислить аномалию ускорения силы тя

жести, нужно или наблюденное значение g отнести к эл

липсоиду, или нормальное значение перенести в точку

наблюдения. Такая операция называется редуцированием,

а поправки, вносимые при этом,— редукциями.

Для редуцирования необходимо знать высоту Н точки

наблюдения над эллипсоидом относимости (рис. 18) и вер

тикальный градиент ускорения силы тяжести. Принципи

ально редуцировать можно и наблюденное значение g на

эллипсоид, и нормальное — на физическую поверхность

Земли. Сначала рассмотрим случай образования аномалий

на физической поверхности Земли. После работ М. С. Моло-

денского, построившего теорию нормальных высот и ре

шившего краевую задачу теории потенциала для физиче

ской поверхности Земли (см. § 3 гл. 5), этот способ редуци

рования и образования аномалий стал преимущественным.

Будем пользоваться в дальнейшем следующими стан

дартными обозначениями: у — нормальное значение силы

тяжести, у о — то же на эллипсоиде, g — наблюденное зна

чение силы тяжести, g'o — то же на геоиде, Ag — смешан

ная аномалия ускорения силы тяжести, £ — аномалия

высоты или высота квазигеоида над эллипсоидом относи

мости, | — высота геоида над эллипсоидом относимости.

Итак, мы знаем нормальное значение ускорения у0

силы тяжести на эллипсоиде относимости, знаем нормаль

ную высоту Нн в точке наблюдения. Рассчитав верти

кальный градиент щ и умножив его на нормальную

высоту, получим поправку к нормальному значению ус

корения силы тяжести у для переноса у к физической

поверхности Земли. Эта поправка будет

знак минус берется потому, что при положительных вы

сотах ускорение силы тяжести на физической поверхности

Земли меньше, чем на эллипсоиде. Однако На не есть

высота физической поверхности Земли над эллипсоидом.

Последняя называется геодезической высотой Н. Она не

определяется из нивелировок и отличается от нормальной

высоты Ни на величину £ — так называемую аномалию

высоты:

Я = Я н + £.

Аномалия высоты равна высоте квазигеоида. Редуцируя

таким образом нормальное значение ускорения силы тя

жести у, мы получаем его в точках, отстоящих от физиче

ской поверхности Земли на расстоянии аномалии высоты £.

Тогда аномалия силы тяжести в точках физической поверх

ности Земли определится формулой

Л£ = * Ф .„ .з .-(т о -Й -Я н)- (4-2)

Слагаемые, составляющие аномалию, относятся к раз

ным поверхностям: g отнесено к физической поверхности

Земли, скобка — к точке, отстоящей от физической по

верхности Земли на аномалию высоты £. Такая аномалия

называется смешанной. Так как она связана с величиной

аномалии высоты £, она несет в себе информацию о ней.

Поэтому смешанные аномалии играют видную роль в

теории фигуры Земли, позволяя получить аномалии высот

£, по которым при известных эллипсоиде и нормальных

высотах с любой подробностью можно построить фигуру

физической поверхности Земли.

Чтобы от смешанных аномалий перейти к чистым, нужно

в первые ввести поправку за высоту £.

Смешанные аномалии, а именно их мы получаем в ре

зультате гравиметрических работ, играют важную роль

и в геофизических проблемах, в том числе в гравитационной

разведке. Они отображают распределение плотностей в

верхних слоях Земли. Обычно в гравиметрии приходится

иметь дело со смешанными аномалиями, поскольку £

изменяется плавно и даже на больших площадях незначи

тельно, поэтому поправка, приводящая смешанную ано

малию к чистой, в большинстве случаев может считаться

постоянной и не приниматься во внимание при геологиче

ском истолковании аномалий. Только для обширных

регионов надо над ней задумываться.

В случаях, когда при образовании аномалий не вво

дится никаких поправок, кроме чистого переноса значения

нормального ускорения у в точку, отстоящую от физической

поверхности Земли на аномалию высоты, получаются так

называемые аномалии в свободном воздухе. Это название

историческое. Оно означало, что редукция происходит

без учета влияния каких-либо промежуточных масс Земли,

а так как влияние воздуха в эпоху, когда была предложена

редукция, не учитывалось, то и считалось, что приведение

происходит в чистом воздухе, свободном от масс Земли.

Сейчас лучше было бы назвать эту редукцию редукцией

в пустоте, поскольку массу атмосферы мы относим тоже к

Земле и ее влияние учитываем. Еще точнее было бы на

звать ее «нормальной*редукцией», так как она осуществ

ляется в нормальном поле Земли, свободном от каких-

либо масс вне уровня нормального эллипсоида.

Образованные описанным способом аномалии могут

усложняться введением различных поправок, в зависимости

от которых аномалии получают свое название. Сглажи

вание рельефа в точке наблюдения и добавление к редук

ции в^свободном воздухе поправок за влияние рельефа

приводит к аномалиям Фая. Вычитание из аномалии в

свободном воздухе влияния масс промежуточного слоя

между “ физической поверхностью ЗемлиТи квазигеоидом

приводит к аномалиям Буге. Вычитание влияния двойного

слоя — к аномалиям Прея, снятие влияния рельефа по

всей Земле — к полной топографической редукции. Далее

все эти поправки будут рассмотрены подробно.

При описанном подходе к образованию аномалий в

свободном воздухе выполняются условия теоремы Стокса:

сохраняется общая масса Земли и отсутствуют массы за

уровенной поверхностью, охватывающей всю Землю. Гра

ничной поверхностью служит в этом случае физическая

поверхность Земли. Возможен другой подход к проблеме,

который можно назвать классическим: это так называемая

регуляризация Земли и отнесение аномалий к поверхности

геоида. Этот подход излагается в следующем параграфе.

§ 2. Редуцирование на геоид. Понятие

регуляризации Земли

Теорема Стокса (гл. 2, § 6) устанавливает единственность

построения потенциала силы тяжести на поверхности Земли

и во всем внешнем пространстве независимо от распреде

ления масс при условии, что за поверхность Земли принята

уровенная поверхность, целиком охватывающая эти массы.

В качестве такой поверхности удобно взять эллипсоид

вращения. Форма Земли действительно очень близка к

этой фигуре. Отклонения геоида от хорошо подобранного

и ориентированного эллипсоида вращения ограничиваются

всего несколькими десятками метров. Задавая уровенную

поверхность в виде эллипсоида вращения, мы должны вы

брать его так, чтобы все массы были внутри него. В самом

деле, ряд, в который’мы разложили потенциал притяжения

(1.41) и (1.51), сходится, только если у < 1 . т. е. при

условии, что нет масс вне поверхности, описываемой ра

диусом-вектором. Таким образом, теория фигуры Земли

должна строиться в предположении, что вне уровенной

поверхности, представляющей Землю, масс нет.

Однако если рассматривать в качестве уровенной по

верхности эллипсоид, наилучшим образом представляющий

Землю, т. е. такой, сумма квадратов отклонений которого

от геоида минимальна, то неизбежно остаются массы, вы

ступающие за поверхность эллипсоида, например конти

ненты. Возникает задача построения такой идеальной

Земли, у которой все массы лежат внутри ограничивающей

ее уровенной поверхности. Операция устранения выступаю

щих за уровенную поверхность масс получила название

регуляризации Земли. Возможны два основных пути

решения этой задачи.

1. Перенесение всех масс тем или иным способом внутрь

уровенной поверхности. При этом в соответствии с теоремой

Стокса (гл. 2, § 5) необходимо позаботиться о том, чтобы

общая масса Земли и форма уровенной поверхности изме

нились по возможности мало. Простое снятие масс без

переноса внутрь вызывает большие деформации уровенной

поверхности и поэтому неудобно при решении задач,

связанных с определением фигуры Земли.

2. Отказ от уровенной поверхности, близко совпадаю

щей с реальной Землей, и построение поверхности отно

симости на высоте, охватывающей все выступающие массы

Земли, например на высоте 10 км (геоид Бриллуэна). Задача

в этом случае может быть решена строго, так как не прихо

дится иметь дело с потенциалом внутри масс, однако реше

ние в этом случае имеет ограниченный практический смысл.

Аномалии на такой поверхности будут сглаженными, а

вводимые поправки большими. Будут ускользать детали

гравитационного поля, важные в таком приложении гра

виметрии, как гравитационная разведка. Наконец, вряд

ли удобно представлять Землю поверхностью, в основном

отдаленной от реальной Земли и приближающейся к ней

лишь в области самых высоких гор, т. е. в небольшом числе

отдельных точек.

В этом смысле геоид Листинга несравненно удобнее,

так как он на двух третях поверхности Земли, т. е. на

океанах, практически совпадает с физической поверхностью

Земли, а на остальной территории проходит в основном

на расстоянии нескольких сотен метров под ней и лишь

в районах плоскогорий и горных цепей отдален на не

сколько километров.

Наблюдения силы тяжести могут производиться на

физической поверхности Земли, на разных высотах над

Землей, под Землей и под водой. Значения силы тяжести,

измеренные в столь различных условиях, должны быть

отнесены к поверхности эллипсоида, или нормальное

поле, заданное на эллипсоиде, должно быть пересчитано

для точек наблюдения. Так возникла редукционная про

блема. При этом должно быть как-то учтено влияние масс,

расположенных между точкой наблюдения и поверхностью

относимости. Здесь редукционная проблема совпадает с

проблемой регуляризации Земли, поскольку в обоих

случаях стоит вопрос о том, как поступить с массами, рас

положенными между точкой наблюдения и поверхностью

относимости. При осуществлении редукции силы тяжести

к уровенному эллипсоиду требуется знать высоты точек

наблюдения над эллипсоидом — так называемые геодези

ческие высоты. Однако эти высоты неизвестны. Из нивели

ровок получаются высоты точек наблюдения над геоидом.

Строго говоря, и это не совсем точно. Геоид практически

неопределим. Строго определены могут быть лишь нор

мальные высоты. С помощью известных нормальных высот

и производится редуцирование силы тяжести.

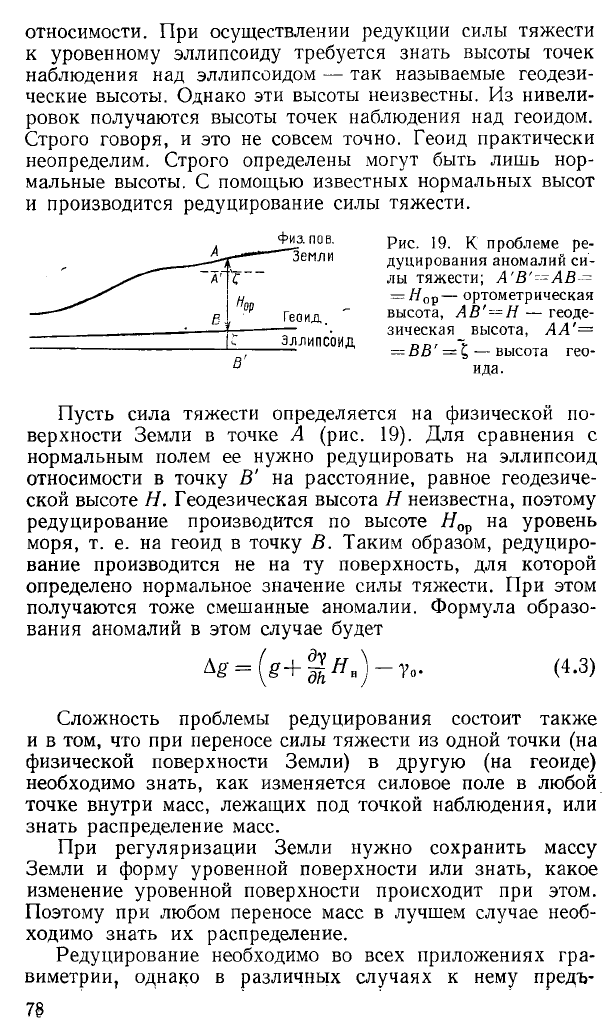
Рис. 19. К проблеме ре

дуцирования аномалий си

лы тяжести; А'В'-=АВ---

= //0р — ортометрическая

высота, АВ’—Н — геоде

зическая высота, АА'=

— ВВ’ = £ — высота гео

ида.

Пусть сила тяжести определяется на физической по

верхности Земли в точке А (рис. 19). Для сравнения с

нормальным полем ее нужно редуцировать на эллипсоид

относимости в точку В’ на расстояние, равное геодезиче

ской высоте Я. Геодезическая высота Я неизвестна, поэтому

редуцирование производится по высоте Яор на уровень

моря, т. е. на геоид в точку В. Таким образом, редуциро

вание производится не на ту поверхность, для которой

определено нормальное значение силы тяжести. При этом

получаются тоже смешанные аномалии. Формула образо

вания аномалий в этом случае будет

Ag = ( g + g t f H) - To. (4.3)

Сложность проблемы редуцирования состоит также

и в том, что при переносе силы тяжести из одной точки (на

физической поверхности Земли) в другую (на геоиде)

необходимо знать, как изменяется силовое поле в любой

точке внутри масс, лежащих под точкой наблюдения, или

знать распределение масс.

При регуляризации Земли нужно сохранить массу

Земли и форму уровенной поверхности или знать, какое

изменение уровенной поверхности происходит при этом.

Поэтому при любом переносе масс в лучшем случае необ

ходимо знать их распределение.

Редуцирование необходимо во всех приложениях гра

виметрии, однако в различных случаях к нему предъ

Физ. по в.

являются разные требования. При решении вопроса о

фигуре Земли и прочих вопросов геодезической грави

метрии необходимо строго соблюдать условие отсутствия

масс вне уровенной поверхности. Из этого приходится

исходить и при выборе редукций. При геологическом ис

толковании результатов гравиметрической съемки совер

шенно безразличны вопросы сохранения общей массы или

общее сохранение формы уровенной поверхности. В этом

случае необходимо редукцию провести так, чтобы в оста

точном аномальном силовом поле наиболее рельефно про

явились особенности распределения масс в данной области.

Таким образом, мы видим, что выбор метода редукции и

решение вопроса регуляризации Земли зависят от того,

какая задача стоит перед исследователем. Вопросам ре

дукций посвящено большое количество работ. Это объ

ясняется, с одной стороны, важностью проблемы, а с дру

гой — сложностью ее и отсутствием безусловно удовле

творительного решения.

§ 3. Редукция в свободном воздухе. Аномалии

в свободном воздухе

Смысл этой редукции состоит в том, чтобы привести

нормальные значения силы тяжести, заданные на нормаль

ном эллипсоиде, к точкам наблюдения, расположенным

на физической поверхности Земли, не принимая при этом

во внимание влияние масс, расположенных между этой

поверхностью и точкой наблюдения. Таким образом, это

редуцирование за высоту, и если известно изменение нор

мальной силы тяжести с высотой, т. е. вертикальный гра

бу

диент ~ , то оно производится просто.

Редукция в свободном воздухе с добавлением поправки

за рельеф местности называется редукцией Фая или Гель

мерта в честь ученых, введших ее в употребление. Выведем

редукцию в свободном воздухе в предположении шарооб

разной Земли. В нашем предположении изменение нор

мальной силы тяжести с высотой

d2W -

M ~ d R ~ d R * ’

где R — радиус модели шаровой Земли.

т GM GM

Имея в виду, что W = и — = у, получим для

вертикального нормального градиента силы тяжести на