Грушинский Н.П. Основы гравиметрии

Подождите немного. Документ загружается.

Сосредоточив основное внимание на вопросах теории и

приложения гравиметрии к изучению Земли, автор не мог

обойти очень интересные достижения в изучении гравита

ционных полей Луны и планет Солнечной системы. Им по

священа последняя глава книги.

Курс рассчитан на студентов астрономических и гео

физических отделений университетов, а также тех вузов,

в которых гравиметрия изучается как один из методов ре

шения основных проблем, а именно вузов геолого-разведоч-

ных и геодезических.

Автор считает приятным долгом поблагодарить своих

рецензентов А. П. Юзефовича, Ю. И. Блоха и А. С. Логи

нова за полезные замечания и советы, благодаря которым

книга была существенно улучшена.

Весьма плодотворными были дискуссии по ряду воп

росов, изложенных в книге, с Н. Б. Сажиной и редактором

3. Н. Левицкой. Обеим им автор также выражает свое ува

жение и приносит глубокую признательность.

ГЛАВА 1

ЭЛЕМЕНТЫ ТЕОРИИ ПРИТЯЖЕНИЯ

§ 1. Притяжение

Согласно закону всемирного тяготения, сформулирован

ному И. Ньютоном (1643— 1727), все тела притягиваются

друг к другу с силой, пропорциональной произведению масс

взаимодействующих тел и обратно пропорциональной квад

рату расстояния между массами. Для двух точечных масс

закон всемирного тяготения можно записать в следующем

виде:

здесь т.х и т 2 — массы, сосредоточенные в точках 1 и 2,

() — расстояние между точками 1 и 2, G — коэффициент

пропорциональности, называемый гравитационной постоян-

Сила F является векторной величиной. Если поместить

начало координат в центр притягивающей массы, то вектор

силы F, действующей на притягиваемую массу, направлен

противоположно ее радиусу-вектору р, поэтому перед си

лой ставят знак минус.

В векторной форме сила притяжения F для точечных

масс М я т запишется в следующем виде:

В случае притяжения единичной массы массой, состоя

щей из отдельных точек, выражение для'/7 следует запи

сать в виде суммы притяжений единичной массы всеми то

чечными массами

(

)

ной.

(1.2)

В случае непрерывного распределения масс сумма ,црлж

на быть заменена интегралом по всему объему масс

(1.3)

Наконец, в случае притяжения двух тел сила опреде

ляется двойным интегралом, взятым по массам обоих тел,

где g — ускорение, развиваемое инерционной массой т под

действием силы F. Если масса инерционная эквивалентна

массе гравитирующей, т. е. значение массы т в выраже

ниях (1.Г) и (1.5) одно и то же, то

Каждой точке пространства в окрестности гравитирую

щей массы М можно приписать значение векторной функ

ции пространственных координат вида (1.6). Такое прост

ранство назовем гравитационным силовым полем, а сам

вектор g — напряженностью поля в этой точке. Численно

напряженность поля равна силе, действующей на единич

ную массу, помещенную в эту точку.

В приведенных выше рассуждениях мы предположили,

что масса, входящая в закон всемирного тяготения, экви

валентна массе второго закона Ньютона или, иными слова

ми, масса тяжелая равна массе инертной. Строго говоря,

это ниоткуда не следует. Определения той и другой масс

независимы. Сам Ньютон это понимал и даже пытался экс

периментально подтвердить эквивалентность этих масс. Од

нако его опыты имели низкую точность. Только через 200

лет после Ньютона венгерский физик Р. Этвеш (1848—

1919) поставил опыт с крутильными весами, доказывающий

постоянство G независимо от химического состава масс, ис

пользовавшихся в эксперименте, а значит, и эквивалент

ность гравитирующей и инертной масс, с точностью Ы б ~ 9.

Еще через 50 лет, в 1963 г. Р. Дике в своем эксперименте

повысил эту точность до Ы 0 -11.

(1.4)

м, мг

Второй закон Ньютона выражается уравнением

F — mg,

(1.5)

Размерность гравитационной постоянной G получим из

(1.1'), введя выражение силы притяжения через ускорение

но второму закону Ньютона

и представив величину ускорения g через время и путь из

формулы

где L — длина, Т — время, М — масса.

В системе СИ, в которой за единицу длины принят метр,

за единицу массы — килограмм и за единицу времени —

секунда, гравитационная постоянная принимает значение

В следующем параграфе будет рассказано о методе опре

деления гравитационной постоянной G и приведен перечень

основных определений этой константы.

§ 2. Гравитационная постоянная О

Коэффициент G является одной из фундаментальных по

стоянных физики и астрономии. В частности, он задает

масштаб масс Солнечной системы. По законам Кеплера

можно выразить массы всех планет Солнечной системы через

массу Солнца, но только зная гравитационную постоянную,

можно установить массу, принятую за единицу, т. е. массу

Солнца, в абсолютной мере и тем самым выразить в абсо

лютной мере массы всех планет. Вообще выразить в абсо

лютной мере силу притяжения между двумя массами можно

только зная величину G. Знание G позволяет также вычис

лить среднюю плотность планет. Однако определение гра

витационной постоянной является довольно сложным фи

зическим экспериментом, и поэтому в ней до сих пор на

дежно определены только три знака после запятой.

Тогда размерность ускорения

и = -р г

н размерность гравитационной постоянной

[Л4]|Т2] ’

G=6,674-10 им3/кг*са.

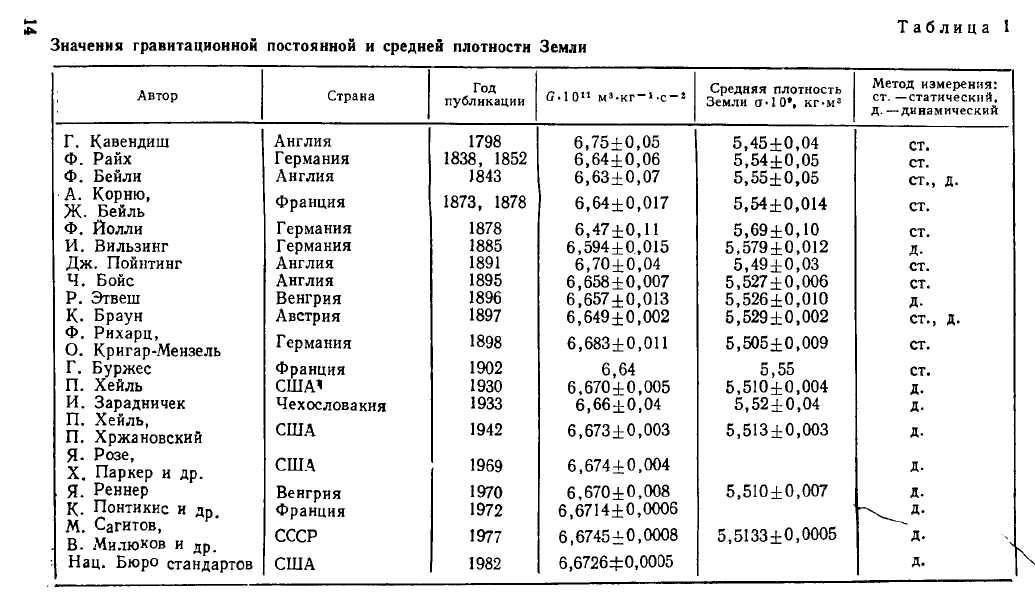
Значения гравитационной постоянной и средней плотности Земли

Таблица 1

; Автор

Страна

Год

публикации

С. 1 О11 м3 *кг—1 *с — 2

Средняя плотность

Земли а - 10*. кг-м3

Метод измерения:

ст. —статический,

д. — динамический

Г. Кавендиш

Англия

1798

6,75±0,05

5,45± 0,04

СТ.

Ф. Райх Германия

1838, 1852 6,64±0,06

5,54±0,05

СТ.

Ф. Бейли

Англия

1843

6,63±0,07

5,55±0,05

ст., д.

А. Корню,

Ж. Бейль

Франция

1873, 1878

6,64 ±0,017

5,54±0,014

ст.

Ф. Йолли

Германия

1878

6,47 ±0,11 5 ,6 9 ± 0 ,10

ст.

И. Вильзинг

Германия

1885

6,594±0,015

5,579 ±0,012

д-

Дж. Пойнтинг

Англия 1891

6,70±0,04

5,49±0,03

СТ.

Ч. Бойс

Англия

1895

6,658 ±0,007 5,527 ±0,006

ст.

Р. Этвеш

Венгрия

1896

6,657±0,013 5,526 ±0,010

Д.

К. Браун Австрия 1897

6,649±0,002 5,529 ±0,002

ст., д.

Ф. Рихарц,

О. Кригар-Мензель

Германия

1898

6,683 ±0,011

5,505±0,009

ст.

Г. Буржес

Франция

1902

6,64

5,55

ст.

П. Хейль

СИШ 1930

6,670±0,005

5,510±0,004

д.

И. Зарадничек

Чехословакия

1933 6,66±0,04

5,52±0,04

д.

П. Хейль,

П. Хржановский

США

1942

6,673±0,003

5,513 ± 0,003

д.

Я- Розе,

X. Паркер и др.

США

1969

6,674+0,004

д.

Я. Реннер

Венгрия

1970

6,670±0,008

5,510±0,007

д.

К. Понтнкис и др.

М. Сагитов,

В. МИЛЮКОВ И др.

Франция 1972

6,6714± 0,0006

СССР

1977

6,6745 ± 0,0008

5,5133± 0,0005

д.

Нац. Бюро стандартов

США

1982

6,6726ф0,0005 д.

В табл. 1 приведена сводка известных определений этого

коэффициента, а также соответствующих значений величи

ны средней плотности Земли.

Гравитационная постоянная G в подавляющем большин

стве случаев определялась с помощью крутильных весов —

одного и? самых чувствительных механических приборов.

Крутильные весы представляют собой подвешенное на тон

кой упругой нити коромысло с равными грузами т на кон

цах. Это колебательная система, возмущаемая подносимы

ми к ней массами М, тем более чувствительная, чем мень

ше коэффициент крутильной жесткости нити

nDd4

Т 32Г ’

где D — модуль сдвига материала, из которого сделана

крутильная нить, I — длина нити, d — диаметр нити.

Дифференциальное уравнение крутильных весов без

учета сил трения имеет вид

/ 5 + Мг (ф) + ЛМф) = 0, (1.7)

где I — момент инерции крутильной системы относительно

вертикальной оси подвеса, M g — момент возмущающих

гравитационных сил, ср — угол закручивания системы от

невозмущенного положения равновесия.

Раскладывая M s(<р) в ряд по степеням малого угла <р

и удерживая члены первого порядка малости, получим

Мг (ф )^ М г (0) + <рМ'(0).

Для малого угла ф выполняется закон Гука, и упругий мо

мент пропорционален углу закручивания:

М т (ф) = тф.

Внося значения моментов в дифференциальное уравнение

(1.7), получим

^ + п \ + с = 0, (1.8)

где

К (0) + т (1.9)

— квадрат собственной частоты крутильной системы,

(1.10)

Mg (0)

Решение уравнения (1.8) распадается на постоянную и

периодическую части и имеет вид

Ф = — + c 1sinn^ ~{~c2cosnt, (1-11)

где Ci и с2 — постоянные интегрирования.

Отсюда следует возможность двух методов Измерения

гравитационной постоянной: статического, корда исполь

зуется решение

Ф 1 = - £ , / 0-12)

и динамического, когда используется вторбе решение

9 2=CiSin nt + CiCosnt. (1-13)

В первом случае измеряется отклонение ф! коромысла под

действием поднесенных к грузам т масс М. Обычно эти

массы подносятся последовательно с двух сторон симмет

рично. Тогда разность углов отклонения согласно (1.12)

и (1.10)

т , + ( Я г ~ м1т^ ж -

Моменты сил притяжения содержат множителем гравита

ционную постоянную G,

M\(0) = GMI(0), M"(0) = GM"(0),

поэтому

G =

-----

— ./я*Аф-■

------

. (1.14)

— (0) + х (0)

Величины I, Mg , M g известны — это параметры уста

новки. Разность углов Лф и частота колебаний п системы

измеряются.

При динамическом методе определяется частота кру

тильных колебаний пх и п2 при двух положениях притяги

вающих масс. Соответствующие им производные моментов

силы притяжения будут LWg(O)]' и Ш ^(0)]'. Используя

равенство (1.9), получим

п _ 1{п\—п!)

(1.15)

В этом выражении частоты пг и п2 измеряются, а осталь

ные величины вычисляются по известным геометрическим

размерам.

§ 3. Потенциал притяжения и его основные свойства

Поле притяжения является потенциальным. Это значит,

что каждой точке пространства соответствует некоторая не

прерывная, имеющая непрерывные производные скалярная

функция V, причем производные от этой функции по на

правлениям осей координат равны проекциям силы на со

ответствующие оси. Это условие можно кратко записать

в виде

V называется потенциалом. Силовое поле, в каждой точке

которого определена потенциальная функция, называют

консервативным. Данному определению удовлетворяет

функци я

которая и есть потенциал притяжения. Интеграл берется

по всем притягивающим массам. Заметим, что в физике по

тенциалом обычно называют величину —V. Для отличия

выражение (1.16) в теории притяжения часто называют си

ловой функцией.

При изучении притяжения удобно оперировать с проек

циями силы на оси декартовых координат х, у, z.

Для Земли выберем за оси координат полярную ось

(г) и два перпендикулярных радиуса экватора (х и у). Обо

значим в этой системе координат притягиваемую точку

А (х, у, г), а притягивающую dM (|, г|, £) (рис. 1). Расстояние

р между точками будет, очевидно, определяться равенством

F = m^V,

где у — оператор градиента

Функция

(1.16)

Рис. 1. Схема размеще-

ния притягиваемой и при- /*

тягивающей точек. У

р2 = (х — |)2 + (у — г))2 + (z — £);

+ ( z - £ ) 2,

ЧМИ(г'|>ська дармаши*^

обласяа

К1БЛ10ТЕКА

а направляющие косинусы силы F — соотношениями,

, „ , дп х —

cos (У7, х) = £

дх |>

С05(ЛЛ/) = | = Ы , } (1.18)

/Е- \ Ф г ~ £ I

cos(F, г) = £ = — . j

Имея это в виду, получим в соответствии с определением

(1.16) производные потенциала по осям координат

0V п Г dM др п Г' dM х— | F /с \

-д- = —G \ — ^- = — G \ —

-------- = — cos (F, х) =

ox J р2 дх J р2 р т 4 '

м м

dV „CdMd р „ [ ' d'My—ц F /п \ ^ У

~т~ = — G \ — i t = — G \ “ Г 2— - = — co s {F, У) = — .

Л/ J р2 ^ J Р Р т т

м м

dV „ГйМдр n CdMz-l F . Fz

-а - = — G \ —- з5- = — G \ —

---------

5 = — C°S ( Л z) = •

dz J р2 дг J PJ Р т т

м м

(1Л9)

Обобщением этого определяющего свойства потенциала

является равенство его производной по любому направле

нию s проекции силы на это же направление, отнесенной

к единичной массе. Имея это в виду, множитель в даль

нейшем будем опускать. Тогда

|£ = -£cos (F, s) = Fss, (1.20)

где s — единичный вектор выбранного направления. Эта

формула легко получается, если взять полный дифферен

циал от V

„г dV , t , dV , . dV ,.

d \ / = = _ < k + _ d y .1. _ d z

и внести в него значения >

^ = Fcos(F, х), dx = dsQOs(s, х),

^=r.Fcos(F, у), rf«/ = dscos(s, у),

—.=aFvo^(F, г), dz = ds cos (s, г).

Находим

dV = Fds [cos (F, x) cos (s, x) + cos (F, у) cos (s, у) +

-fcos (F, z) cos (s, z)] — Fdscos(F, s). (1.2

Формула (1.21) разъясняет физическую сущность поте!

циала как работы. Она указывает, что приращение потенцк

ала равно работе, совершенной силой F на перемещении ds

Потенциальная функция обладает некоторыми за меча

тельными свойствами. Основные из них мы здесь рассмот

рим, имея в виду, что они будут

полезны нам в дальнейшем изло

жении.

1.Непрерывность и

регулярность. Потенциал

притяжения является функцией

непрерывной и имеет непрерывные

первые и вторые производные во

всей конечной области. На беско- рис. 2. К выводу свойства

нечности потенциал является ре- регулярности потенциала,

гулярной функцией, т. е. при стре

млении р к бесконечности потенциал V стремится к нулю

так, что их произведение остается конечной величиной

lim pV=GM . (1.22)

р->- 00

Это равенство легко доказать, если написать значения по

тенциала, возбуждаемого в точке

(рис.

каким-либо те

лом, и потенциалов, возбуждаемых массами, равными мас

се рассматриваемого тела, но сосредоточенными в точках,

ближайшей к Л и самой удаленной. Тогда можем написать

неравенство

G - < V < < ? - ,

(>1 Р2

где pi — расстояние от А до ближайшей точки тела, р2 —

расстояние от А до наиболее далекой точки тела.

Умножая это неравенство на р и переходя к пределу при

р -> о о , получаем искомое соотношение, поскольку

lim — = lim — = 1.

р->-ао Pi р->-ао Рз

2. Уровенные поверхности. Линии, вдоль

которых действуют силы, называются силовыми линиями.

Поверхности, всюду перпендикулярные силовым линиям,

называются уровенрыми поверхностями (рис. 3). На этих по-

1SL