Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике

Подождите немного. Документ загружается.

10

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

… … … … … … … …

… a

… … … … … … … …

… a

Стоимость 1 единицы корма c

… c

Число единиц корма x

… x

Обозначим через x

число единиц корма ,

входящего в рацион. Тогда этот рацион будет вклю-

чать:

Так как содержание питательных веществ S

долж-

но быть не менее b

, получим систему неравенств:

Кроме того, x

≥ 0.

Общая стоимость рациона F составит:

Итак, ЭММ задачи: составить рацион ,

удовлетворяющий системе ограничений (4.4) и условию

неотрицательности (4.5), при котором функция (4.6)

принимает максимальное значение, то есть

(4.4)

(4.5)

(4.6)

11

Математические методы и модели в экономике

4.1.2. Симплексный метод решения

задач линейного программирования

Для канонической формы записи разработан об-

щий алгоритм решения задач линейного программи-

рования, называемый симплексным методом.

Практические расчеты при решении реальных за-

дач симплексным методом выполняются в настоящее

время с помощью компьютеров. Однако если расче-

ты осуществляются без ЭВМ, то удобно использовать

симплексные таблицы.

Для определенности считаем, что решается задача

на максимум, то есть:

1) Приведем стандартный вид к каноническому.

Для этого введем m штук (по количеству неравенств в

системе ограничений) дополнительных неотрицатель-

ных переменных . Получим следующую

систему:

(4.7)

(4.8)

(4.9)

12

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Эта система называется расширенной.

2) Исходную расширенную систему заносим в пер-

вую симплексную таблицу:

Таблица 4.3

Ба-

зис

Сво-

бод-

ные

члены

Переменные

О.О

… x

n+1

… x

n+m

n+1

… a

1 … 0

n+2

… a

0 … 0

… … … … … … … … …

n+m

… a

0 … 1

F 0 –c

–c

… –c

0 … 0

Последняя строка называется оценочной строкой.

Далее таблица преобразуется по определенным

правилам.

3) Проверяем выполнение критерия оптималь-

ности.

Если в оценочной строке отсутствуют отрицатель-

ные элементы, то найденное решение является опти-

мальным (для задачи на max). Достигнут максимум (в

левом нижнем углу таблицы). Базисные переменные

принимают значения, записанные во втором столбце,

остальные переменные равны нулю.

4) Если критерий оптимальности не выполнен, то

наибольший по модулю отрицательный коэффициент

< 0 в оценочной строке определяет разрешающий

столбец S.

Составляем оценочные отношения каждой строки

по следующим правилам: делим построчно столбик b

на столбец S и получаем:

1

Математические методы и модели в экономике

•

∞, если b

и a

имеют разные знаки;

•

∞, если еслиесли b

= 0 и 0 и0 и и a

< 0;< 0;

•

∞, если еслиесли a

= 0;= 0;

•

0, если0, если a

> 0 и> 0 и и b

= 0;;

•

если b

и a

имеют одинаковые знаки.

Вместо ∞ в оценочных отношениях можно ставить

просто прочерк (–).

Далее определяем минимум оценочных отношений

(среди ненулевых). Если конечного минимума нет, то

задача не имеет конечного оптимума ( ).

Если минимум конечен, то выбираем строку q, на

которой он достигается (любую, если их несколько), и

назовем ее разрешающей строкой.

На пересечении разрешающей строки и разрешаю-

щего столбца находится разрешающий элемент a

5) Переход к следующей таблице осуществляется

по правилам:

а) в крайнем левом столбце записываем новый ба-

зис: вместо переменной x

записываем переменную x

, а

остальные переменные базиса остаются нетронутыми;

б) в столбцах, соответствующих базисным пере-

менным, проставляем: 1 против «своей» базисной пе-

ременной, 0 против «другой» базисной переменной; 0

в оценочной строке для всех базисных переменных;

в) новую строку под номером q получаем из разре-

шающей строки делением всех ее элементов на разре-

шающий элемент a

;

г) все остальные элементы таблицы вычисляем

по правилу прямоугольника:

(4.10)

1

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

6) Далее возвращаемся к пункту 3) этого алгоритма.

Пример

Решить симплексным методом задачу об использо-

вании ресурсов.

1. Приведем к каноническому виду. Для этого вве-

дем дополнительные неотрицательные переменные

≥0, xx

≥0. Получим:

2. Заполняем симплексную таблицу:

Ба-

зис

Оценочные

отношения

18 1 3 1 0 0 0

13 2 1 0 1 0 0

5 0 1 0 0 1 0

21 3 0 0 0 0 1 –

F 0 –2 –3 0 0 0 0

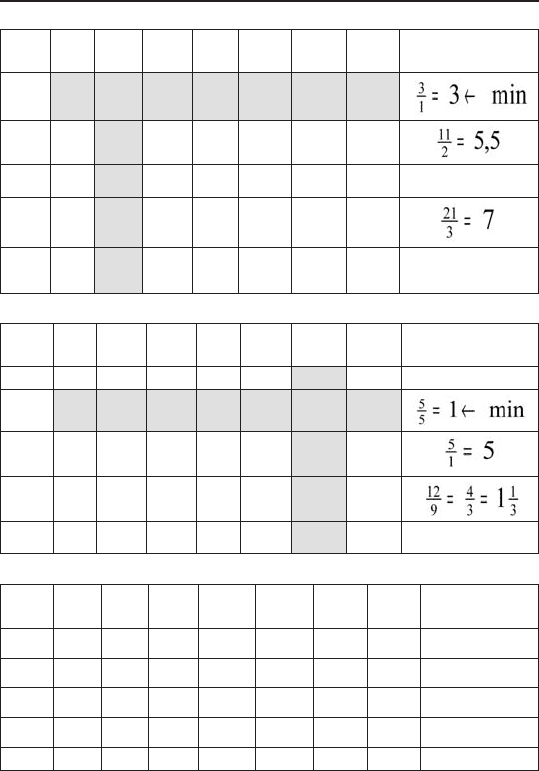
1

Математические методы и модели в экономике

Ба-

зис

Оценочные

отношения

3 1 0 1 0 –3 0

11 2 0 0 1 –1 0

5 0 1 0 0 1 0



21 3 0 0 0 0 1

F 15 –2 0 0 0 3 0

Ба-

зис

Оценочные

отношения

3 1 0 1 0 –3 0 –

5 0 0 –2 1 5 0

5 0 1 0 0 1 0

12 0 0 –3 0 9 1

F 21 0 0 2 0 –3 0

Ба-

зис

Оценочные

отношения

6 1 0 1/5 3/5 0 0

1 0 0 –2/5 1/5 1 0

4 0 1 2/5 –1/5 0 0

3 0 0 3/5 –9/5 0 1

F 24 0 0 4/5 3/5 0 0

В оценочной строке нет отрицательных элементов,

значит, выполнен критерий оптимальности:

max

= 24 при X* = (6; 4; 0; 0; 1; 3) или X* = (6; 4).

1

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Вывод. Предприятие получит максимальную при-

быль в размере 24 у. д. е. (F*

max

= 24), если будет

выпускать 6 единиц продукции P

= 6) и 4 единицы

продукции P

= 4).

Дополнительные переменные x

, x

, xx

и x

показы-

вают разницу между запасами ресурсов каждого вида

и их потреблением, то есть остатки ресурсов. Таким

образом, при оптимальном плане ресурсы S

и S

будут

израсходованы полностью (x

= x

= 0), ресурса S

оста-

нется 1 ед. (x

= 1), ресурса S

останется 3 ед. (x

= 3).

4.1.3. Взаимно двойственные задачи

линейного программирования и их

свойства

Ранее была рассмотрена задача об использовании

ресурсов (экономико-математическая модель и содер-

жательная интерпретация этой задачи I представленыI представлены представлены

в левой части таблицы 4.3). В приведенной модели b

(i = 1, 2, …, m) обозначает запас ресурса S

; a

— чис-

ло единиц ресурса S

, потребляемого при производстве

единицы продукции P

(j = 1, 2, …, n); c

— прибыль

(выручка) от реализации единицы продукции PP

(j = 1,

2, …, n) (или цена продукции P

Предположим, что некоторая организация решила

закупить ресурсы S

, S

,…, S

предприятия и необхо-

димо установить оптимальные цены на эти ресурсы

, y

, …, y

. Очевидно, что покупающая организация

заинтересована в том, чтобы затраты Z на все ресурсыZ на все ресурсы на все ресурсы

в количествах b

, b

, …, b

по ценам соответственно

, y

, …, y

были минимальны, то есть

С другой стороны, предприятие, продающее ресур-

сы, заинтересовано в том, чтобы полученная выручка

была не менее той суммы, которую предприятие может

получить при переработке ресурсов в готовую продук-

(4.11)

1

Математические методы и модели в экономике

цию. На изготовление единицы продукции P

расхо-

дуется a

единиц ресурса S

, a

единиц ресурса S

…, a

единиц ресурса S

, …, a

единиц ресурса S

по

цене соответственно y

, y

, …, y

. Поэтому для удов-

летворения требований продавца затраты на ресурсы,

потребляемые при изготовлении единицы продукции

, должны иметь не менее ее цены c

, то есть

Аналогично можно составить ограничения в виде

неравенств по каждому виду продукции P

, PP

, …, P

Экономико-математическая модель и содержательная

интерпретация полученной таким образом двойствен-

ной задачи II приведены в правой части таблицы 4.4.II приведены в правой части таблицы 4.4. приведены в правой части таблицы 4.4.

Таблица 4.44.4.4

Задача I (исходная)I (исходная) (исходная) Задача II (двойственная)II (двойственная) (двойственная)

(4.13)

(4.14)

и условии

неотрицательности

≥ 0, x

≥ 0, ..., x

≥ 0

(4.15)

Составить такой план вы-

пуска продукции X = (x

, x

..., x

), при котором прибыль

(выручка) от реализации

продукции будет максималь-

ной при условии, что потреб-

ление ресурсов по каждому

виду продукции не превзой-

дет имеющихся запасов.

(4.16)4.16).16)16))

(4.17)

и условии неотрицательности

≥ 0, y

≥ 0, ..., y

≥ 0

(4.18)

Найти такой набор цен (оценок)

ресурсов Y = (y

, y

, ..., y

), при

котором общие затраты на ре-

сурсы будут минимальными при

условии, что затраты на ресур-

сы при производстве каждого

вида продукции будут не менее

прибыли (выручки) от реализа-

ции этой продукции.

(4.12)

1

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Рассмотрим формально две задачи I и II. Эти зада-I и II. Эти зада- и II. Эти зада-II. Эти зада-. Эти зада-

чи обладают следующими свойствами:

1. В одной задаче ищут max линейной функции, вВ одной задаче ищут max линейной функции, в

другой — min.

2. Коэффициенты при переменных в линейной (це-

левой) функции являются свободными членами

системы ограничений в другой.

3. Каждая из задач задана в стандартной форме,Каждая из задач задана в стандартной форме,

причем в задаче максимизации все неравенства

вида ≤, а в задаче минимизации все неравенства

вида ≥.

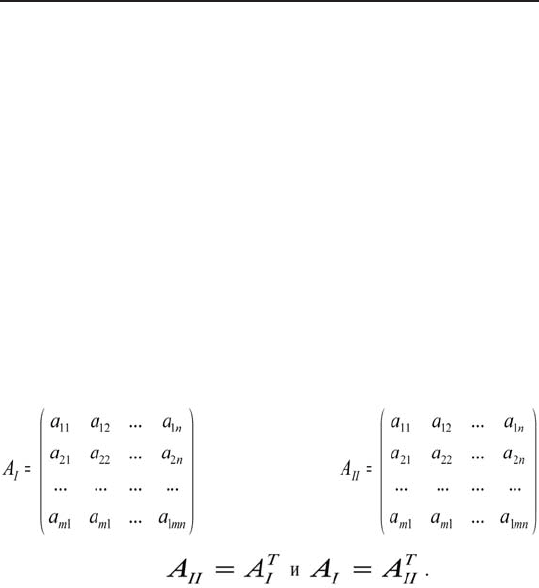
4. Матрицы коэффициентов при переменных в сис-

темах ограничений обеих задач являются транс-

понированными друг к другу, то есть:

у задачи I у задачи III у задачи II у задачи IIII

Таким образом:

5. Число неравенств в системе ограничений однойЧисло неравенств в системе ограничений одной

задачи совпадает с числом переменных в другой

задаче.

6. Условия неотрицательности переменных имеются

в обеих задачах.

Две задачи I и II линейного программирования, об-I и II линейного программирования, об- и II линейного программирования, об-II линейного программирования, об- линейного программирования, об-

ладающие указанными свойствами, называются симп-

лексными взаимно двойственными задачами.

В дальнейшем будем говорить просто «двойствен-

ные задачи».

Исходя из определения, можно предположить сле-

дующий алгоритм составления двойственной задачи:

1. Привести все неравенства системы ограниче-Привести все неравенства системы ограниче-

ний задачи к одному смыслу: если задача на

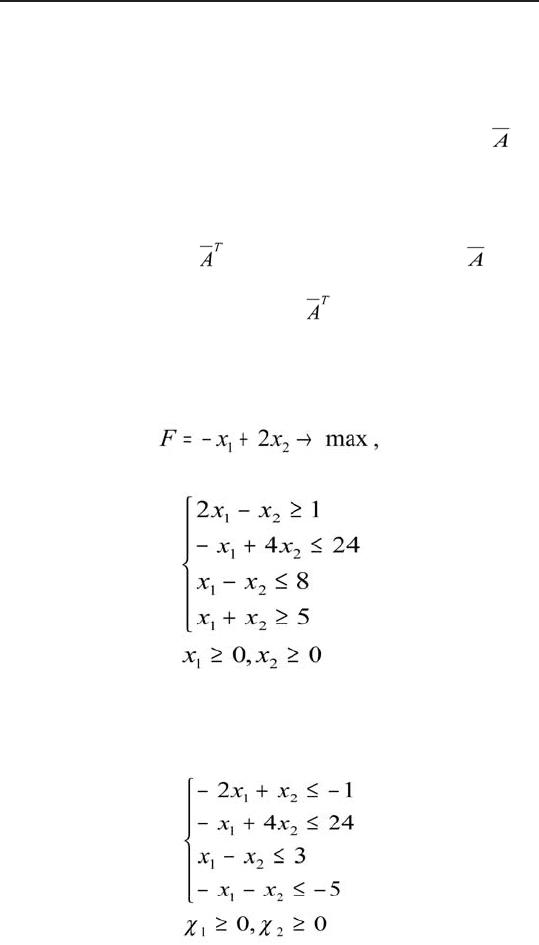
1

Математические методы и модели в экономике

максимум, то все неравенства со знаком ≤,

если на минимум — ≥. Для этого неравенства,

в которых данное требование не выполняется,

умножить на (–1).

2. Составить расширенную матрицу системыСоставить расширенную матрицу системы , в

которую включить матрицу коэффициентов при

переменных A, столбец свободных членов и стро-

ку коэффициентов при переменных в целевой

функции.

3. Найти матрицуНайти матрицу , транспонированную к .

4. Сформулировать двойственную задачу на основа-Сформулировать двойственную задачу на основа-

нии полученной матрицы и условия неотрица-

тельности переменных.

Пример

Составить задачу, двойственную данной:

при ограничениях:

Решение

1. Задача на максимум, значит, все неравенства в

системе ограничений должны быть ≤, то есть (1) и (4)

неравенства умножаются на (–1). Получим: