Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике
Подождите немного. Документ загружается.


10
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
При неизменной норме, эквивалентной норме за-
меняемости в плановом периоде, значения q
1
и q
2
най-
дем, решая совместно заданное уравнение функции
потребления и прямой предпочтения:
q
2
– 25 = 0,6(qq
1
– 45);
�0qq
1
– q
1
2
+ 50q
2
– q
2
2
= 2000.
При подстановке q
2,
выраженного из первого урав-
нения, получаем два корня q
1
= 23,14 и q
2
= 66,66.
Второй корень необходимо отбросить как нереальный.
Тогда значение q
2
= 11,9, то есть примерно 11–12 штук.
Следовательно, при неизменной эквивалентной норме
заменяемости, при увеличении расхода на путевки до
2000 руб., то есть на (2000/1800 –1) 100% = 11,1%,
число туристических путевок увеличится на 4 штуки,
или на 20%, а число путевок санаторно-курортного
лечения — на 2 шт., то есть примерно на 24%. Та-
ким образом, при определении предложения путевок
санаторно-курортного типа в плановом периоде будем
иметь:
•
для варианта а), когда предложение остается
на уровне базового периода, из уравнения 2000 =
= 90qq
1
– q
1
2
+ 50 • 10 – 10• 10 – 10
2
находится число ту-
ристических путевок. Оно будет равно примерно
24–25 штукам, а предельная норма заменяемости
определится из соотношения:
γ = – (25 – 10)/(45 – 24) = – 0,73; 10)/(45 – 24) = – 0,73;
•
для варианта б) число туристических путевок
будет примерно равно 21–22 штукам, а γγ = – 0,42;
•
для варианта в) qq
1
= 20 и γ = – 0,2.
Результаты анализа говорят о том, что с ростом
предложения путевок санаторно-курортного лечения
число туристических путевок незначительно снижа-
ется, а эквивалентная норма заменяемости этих благ
резко дифференцируется.

11
Математические методы и модели в экономике
4) Строятся функции спроса из функций потреб-
ления.
Если имеется целевая функция потребления, извес-
тен доход (бюджет) покупателей и цены благ, то мож-
но получить и функции спроса, исходя из гипотезы,
что потребитель тратит весь свой бюджет на приобре-
тение рассматриваемого набора благ.
Предположим, что средняя стоимость туристичес-
кой путевки составляет ��
1
= 50 руб., путевки санатор-
но-курортного лечения — ��
2
= 130 руб. Установлено
также, что на приобретение путевок в год фирма мо-
жет выделить а) 10 000 руб. и б) 100 000 руб.
Найти функцию спроса для целевой функции пот-
ребления путевок на предприятии в целом и определить
оптимальный спрос на путевки для вариантов а) и б).
Распределение средств на приобретение путевок, оче-
видно, осуществляется в соответствии с выражением:
Z = p = pp
1
q
1
+ pp
2
q
2
,
где Z — затрачиваемые средства (доход потреби-Z — затрачиваемые средства (доход потреби- затрачиваемые средства (доход потреби-
телей).
Чтобы найти наибольшую величину уровня пот-
ребления по целевой функции потребления при таком
распределении дохода, нужно приравнять к нулю пол-
ный дифференциал функции потребления:
dU = = (90 – 2q
1
)dqdq
1
+ (50 – 2q
2
)dqdq
2
= 0.
при приращениях, удовлетворяющих условию:
p
1
dq
1
+ pp
2
dq
2
= 0.
Из этих уравнений получаем: q
2
– 25 = (pp
2
/
p
1
)(qq
1
–
– 45). Полученное уравнение представляет собой
уравнение прямой предпочтения с наклоном
γ = (pp
2
/
p
1
).
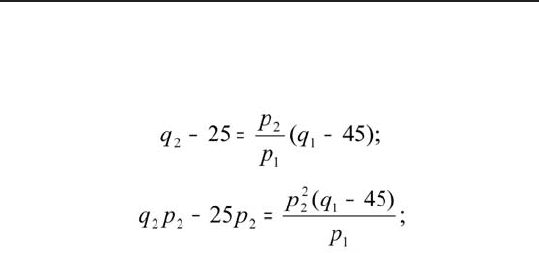
12
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
Это уравнение решается совместно с уравнением
распределения средств на путевки, откуда получаются
уравнения спроса:
q
2
pp
1
p
2
– 25 pp
1
p
2
= pp
2
2
q
1
– 45 pp
2
2
;
так как q
2
= (Z – pZ – p – pp
1
q
1
) / pp
2
, то
p
1
(Z – p
1
q
1
) – 25 p
1
p
2
= p
2
2
q
1
– 45 p
2
2
;
p
1
Z – p
1
2
q
1
– 25 p
1
p
2
= p
2
2
q
1
– 45 p
2
2
;
p
1
Z – –25 pp
1
p
2
+ 45 pp
2
2
=( pp
1
2
+ pp
2
2
)qq
1
;
таким образом:
q
1
= (�
1
Z – 25 pp
1
pp
2
+ 45 pp
2
2
) / ( pp
1
2
+ p
2
2
).
Аналогично находим q
2
:
q
2
= (pp
2
Z – 45 pp
1
p
2
+ 45 pp
1
2
) / ( pp
1
2
+ p
2
2
).
Тогда оптимальный спрос на путевки:
•
для варианта а):
q
1
= (50 · 10 000 – 25·50·130 + 45•130
2
) /
/ ( 50
2
+ 130
2
) = 56,6 ≈ 57 шт.
q
2
=
(130•10 000 – 45•50•130 + 25•50
2
) /
/ ( 50
2
+ 130
2
) = 55,22 ≈ 55 шт.
•
для варианта б):
(3.28)
(3.29)

1
Математические методы и модели в экономике
q
1
= (50•100 000 – 25•50•130 + 45•130
2
) /
/ (50
2
+ 130
2
) = 288,6 ≈ 289 шт.
q
2
= (130•100 000 – 45•50•130 + 25•502) /
/ (50
2
+ 130
2
) = 668,2 ≈ 668 шт.
5) Проводится анализ функций спроса.
Чтобы определить характер рассматриваемых благ
(путевок), необходимо рассчитать эластичности их
спроса по доходу и по цене, а также частные эластич-
ности замены.
Эластичность спроса по доходу определяется по
формуле:
Эластичность спроса по цене определяется по
формуле:
Частные эластичности замены определяются по
формуле:
где k — — доля суммарного дохода, затраченного на
благо q
i
, величина которого определяется по формуле
При i = j = jj имеем прямую эластичность по цене,
при i ≠ j —j — — перекрестную эластичность.
замечание
При расчете эластичностей использовать в фор-
мулах (3.30) — (3.32) выражения (3.28) и (3.29) для
q
1
и q
2
.
(3.30)
(3.31)
(3.32)

1
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
Для варианта а) эластичность по спросу на бла-
га первого вида будет равна 0,45, на блага второго
вида — 1,21; эластичности для варианта б): по пер-
вому благу — 0,89; по второму — 1,02.
Соответственно эластичности по цене будут равны:
•
для варианта а) Е
11
= 0,06; Е
22
= – 0,8; Е
12
= – 0,5;
Е
21
= – 0,41;
•
для варианта б) Е
11
= 0,61; Е
22
= – 0,�6;
Е
12
= – 1,5; Е
21
= – 0,26.
Частные эластичности замены:
•
для варианта a)a)) S
12
= –1,15; S
21
= –2,65;
•
для варианта б) SS
12
= –2,64; SS
21
= –2,�2.
На основе изучения величин эластичностей по до-
ходу можно заключить, что путевки туристического
вида являются неэластичными по доходу и представ-
ляют для вариантов необходимые блага. Путевки са-
наторно-курортного лечения эластичны по доходу и
имеют, следовательно, характер предмета относитель-
ной роскоши. Оба вида благ для варианта а) не яв-
ляются эластичными по цене. Эластичными по пере-
крестной цене являются лишь туристические путевки
по второму варианту. Так как все частные эластич-
ности замены отрицательны, можно заключить, что
туристические путевки и путевки санаторно-курорт-
ного лечения являются неконкурирующими взаимодо-
полняющими благами.
Вопросы по теме
Дать определения функций потребления и спроса.
Что называется показателями эластичности для
этих функций и как они аналитически определяются?
Как содержательно трактуются значения показате-
лей эластичности?
Как осуществляется переход от функций предло-
жения к функциям спроса?
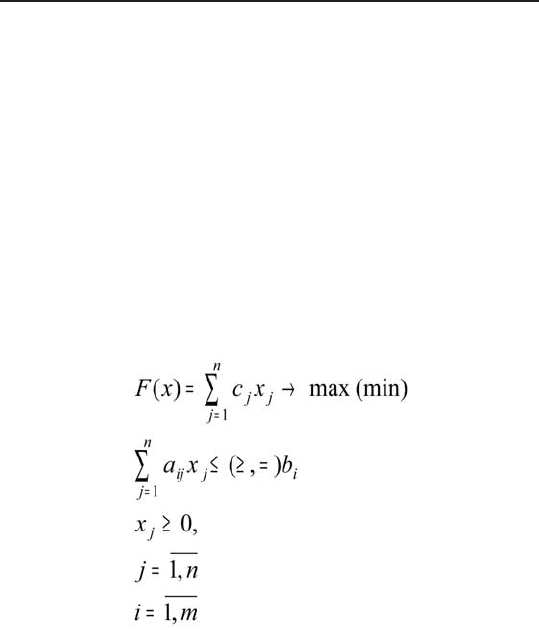
1
Математические методы и модели в экономике
ГЛАВА 4
ОПТИМИзАцИОННЫЕ МЕТОДЫ И
МОДЕЛИ В УПРАВЛЕНИИ
ЭКОНОМИЧЕСКИМИ СИСТЕМАМИ
4.1. Линейное программирование
Задачей линейного программирования называется
задача исследования операций, математическая мо-
дель которой имеет вид:
При этом система линейных уравнений и нера-
венств, определяющая допустимое множество решений
задачи, называется системой ограничений задачи
линейного программирования, а линейная функция
F(x)(x)x)) называется целевой функцией, или критерием
оптимальности.
Задачи линейного программирования могут быть
записаны в трех формах в зависимости от постановки
задачи.
1. Стандартная (или симметричная) форма записи:

1
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
или
2. Основная (или каноническая) форма записи:
3. Общая форма записи.
В ней для отдельных ограничений могут присутство-
вать как знаки равенства, так и знаки неравенства.
Любая форма записи приводится к любой другой.
Например, чтобы перейти от стандартной задачи к
канонической необходимо ввести новые переменные,
а затем в зависимости от знака неравенства либо при-
бавить (задача о ресурсах), либо вычесть (задача о
рационе) их из каждого неравенства.
Пример
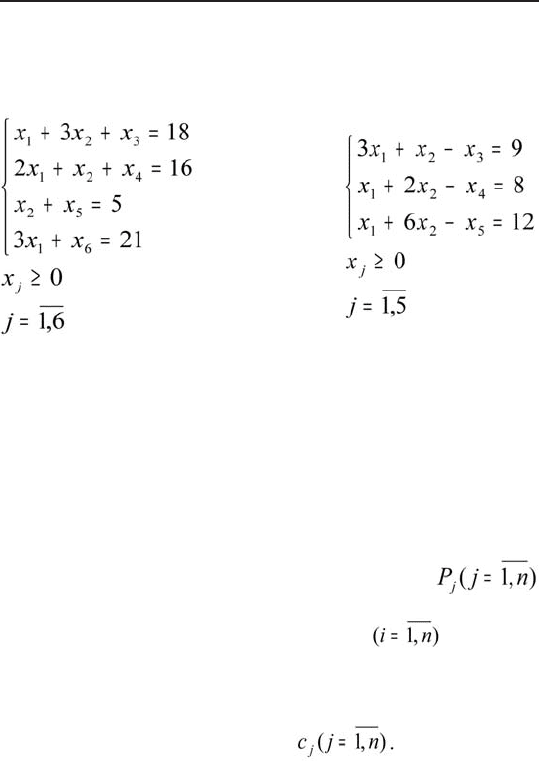
1
Математические методы и модели в экономике
1. Введем дополнительные неотрицательные пере-
менные x
3
≥0, x
4
≥0, xx
5
≥0, xx
6
≥0. Получим новую систему
ограничений.
4.1.1. �остроение �кономико-�остроение �кономико-
математических моделей задач линейного
программирования
Рассмотрим процесс построения математических
моделей задач линейного программирования на при-
мерах.
Задача об использовании ресурсов
Для изготовления n видов продукции
предприятие использует m видов сырья S
1
, S
2
,..., S
m
.
Запасы ресурса S
i
составляют в i ед. .
Известны также технологические коэффициенты a
ij
—
число единиц ресурса S
i
, затрачиваемого на изготов-
ление единицы продукции P
j
. Прибыль от реализации
единицы продукции P
j
равна
Необходимо составить такой план выпуска продук-
ции, при котором прибыль от ее реализации была бы
максимальной.
Составим экономико-математическую модель за-
дачи.
Для этого условие задачи для наглядности занесли
в таблицу 4.1.
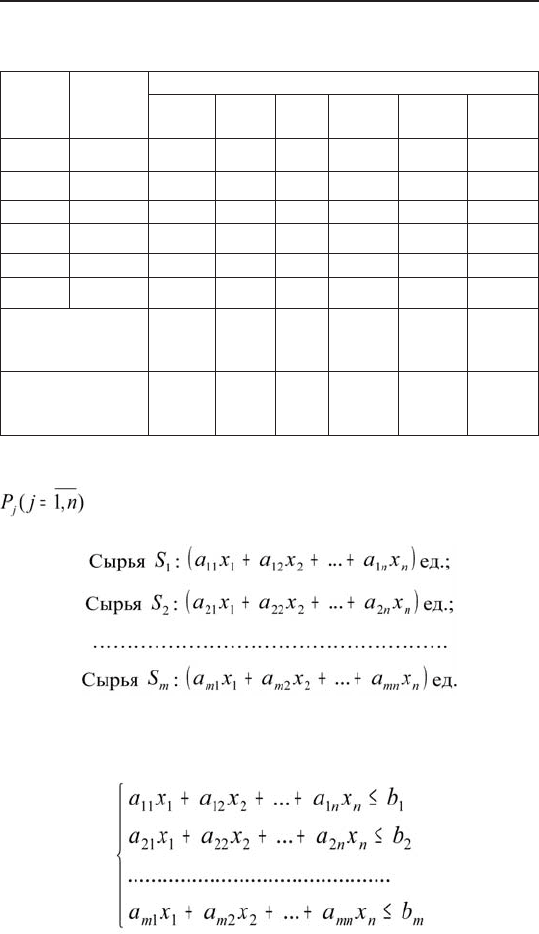
1
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
Таблица 4.1
Вид Запасы Технологические коэффициенты
сырья сырья P
1
P
2
… P
j
… P
n
S
1
b
1
a
11
a
12
… a
1j
… a
1n
S
2
b
2
a
21
a
22
… a
2j
… a
2n
… … … … … … … …
S
i
b
i
a
i1
a
i2
… a
ij
… a
in
… … … … … … … …
S
m
b
m
a
m1
a
m2
… a
mj
… a
mn
Прибыль от
реализ. ед. ед.ед.
продукции
c
1
c
2
… c
j
… c
n
Колич. ед.
продукции к
выпуску
x
1
x
2
… x
j
… x
n
Обозначим через x
j
число единиц продукции
, запланированных к выпуску. Для их изго-
товления потребуется:
Так как потребление ресурсов не должно превы-
шать их запасов, то связь между потреблением ресур-
сов и их запасами выразится системой неравенств:
(4.1)
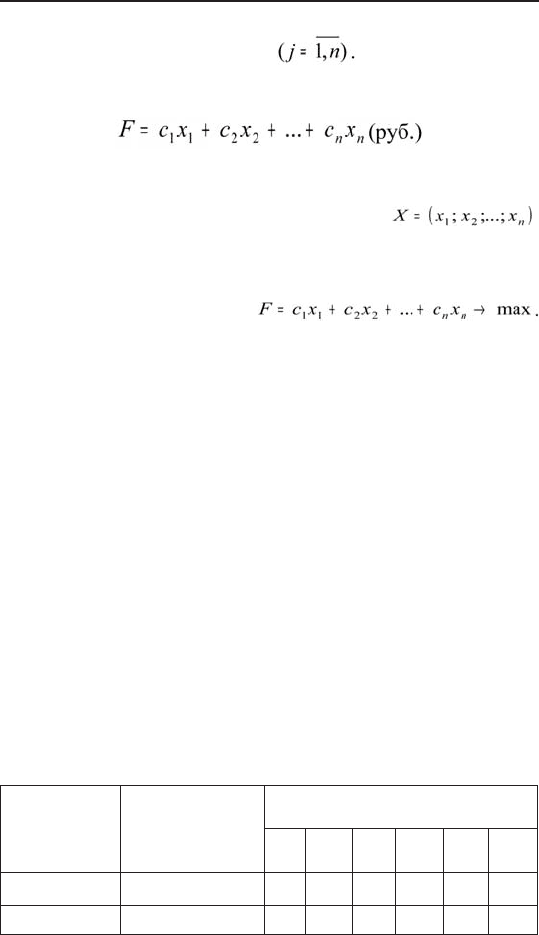
1
Математические методы и модели в экономике
По смыслу задачи x
j
≥ 0
Суммарная прибыль F составит
Итак, экономико-математическая модель.
Найти такой план выпуска продукции ,
удовлетворяющей системе (4.1) и условию (4.2), при
котором функция (4.3) принимает максимальное зна-
чение.
Это записывается так:
Задача о составлении рациона
(задача о диете, задача о смесях)
Имеется n видов корма, содержащих питательные
вещества S
1
, S
2
,..., S
m
. Известно число единиц пита-
тельного вещества S
i
в единице корма A
j
(обозначим
(a
ij
), а также необходимый минимум содержания в
рационе питательного вещества S
i
, равный b
i
(i = 1,
2, …, m).
Стоимость единицы корма A
j
равна стоимости кор-
ма c
j
руб. (j = 1, 2 … n).
Необходимо составить рацион, имеющий мини-
мальную стоимость, в котором содержание каждого
вида питательных веществ было не менее установлен-
ного предела.
Составим экономико-математическую модель задачи.
Таблица 4.2
Питатель-
ное вещес-
тво
Необх. min
питательных
веществ
Число единиц питательного
вещества в 1 единицу корма
A
1
A
2
… A
j
… A
n
S
1
b
1
a
11
a
12
… a
1j
… a
1n
S
2
b
2
a
21
a
22
… a
2j
… a
2n
(4.2)
(4.3)
