Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике
Подождите немного. Документ загружается.

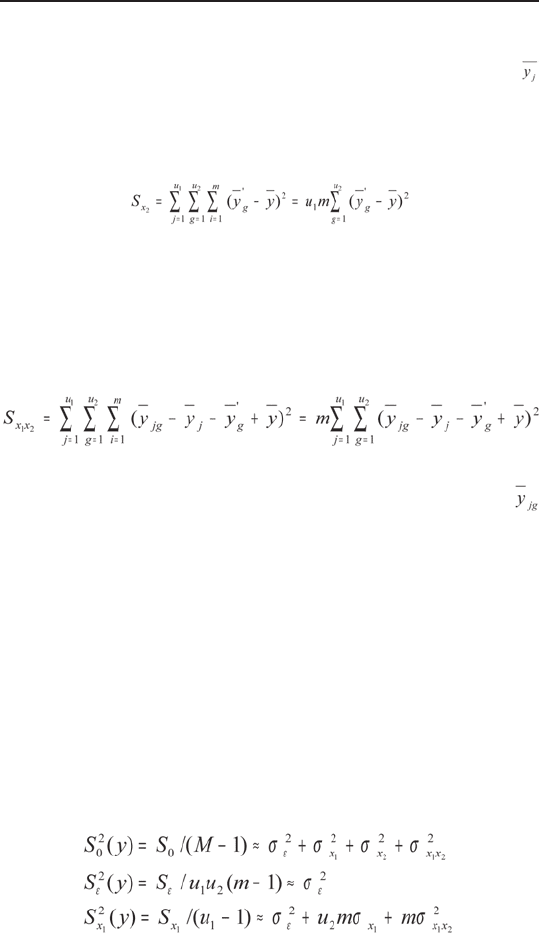
110
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
— сумма квадратов отклонений между строками.
Сумма S
x
1
/(u
1
m) характеризует рассеяние средних
по строкам в результате действия фактора случайнос-
ти с дисперсией среднего для строки σ
2
ε
(u
2
m), фактора
Х
1
с дисперсией σ
2
x
1
и фактора взаимодействия с дис-
персией среднего для строки σ
2
x
1
x
2
/u
2
Величина
— сумма квадратов отклонений между столбцами.
Сумма S
x
2
/(u
1
m) характеризует рассеяние средних по
столбцам в результате действия фактора случайности
с дисперсией среднего для столбца σ
2
ε
(u
1
m) фактора
Х
2
с дисперсией σ
2
x
2
и фактора взаимодействия Х
1
Х
2
с
дисперсией среднего для столбца σ
2
x
1
x
2
/u
1
.
Величина
— сумма квадратов отклонений между сериями.
Сумма σ
2
x
1
x
2
/m характеризует рассеяние средних
серий в результате действия фактора случайности с
дисперсией среднего серии σ
2
ε
/m и фактора взаимо-
действия с дисперсией σ
2
x
1
x
2
.
Каждая из сумм квадратов отклонений S
o
, S
ε
,S
x
1
,
S
x
2
, S
x
1
x
2
, поделенная на отвечающее ей число степеней
свободы k
o
, k
ε
, k
x
1
, k
x
2
, k
x
1
x
2
, дает несмещенную оценку
соответствующей дисперсии. Величины степеней сво-
боды определяются по формулам:
k
0
=M – 1; k
ε
= u
1
u
2
(m – 1);
k
x
1
=
u
1
– 1; k
x
2
=
u
2
– 1; k
x
1
x
2
=
(u
1
– 1)(u
2
– 1).
Тогда дисперсии равны:
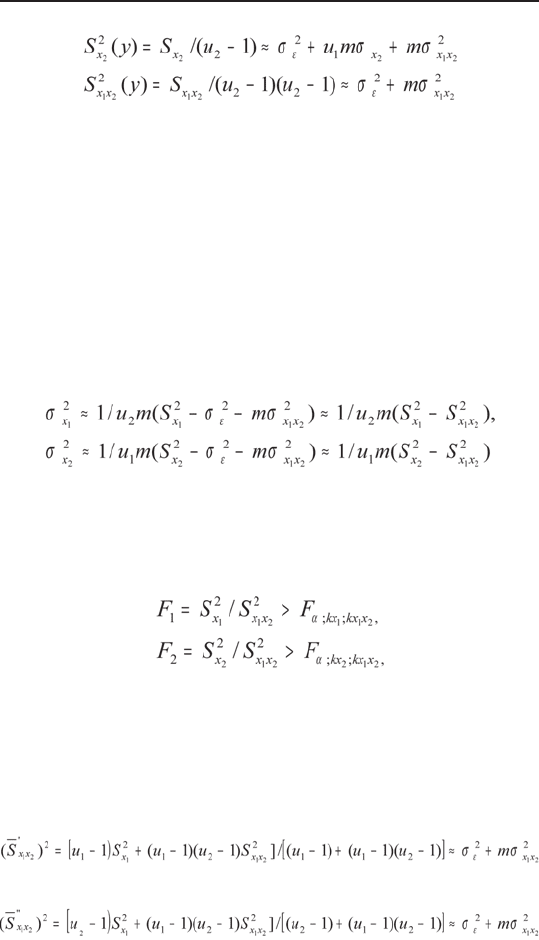
111
Математические методы и модели в экономике
Правильность подсчета чисел степеней свободы
проверяется по соотношению
k
o
= k
ε
+ k
x
1
+ k
x
2
+ k
x
1
x
2
Анализ существенности влияния факторов Х
1
и Х
2
и их взаимодействия Х
1
Х
2
производят на основании
критерия Фишера при выбранном уровне значимости
а в следующем порядке:
1. Влияние факторов Х
1
и Х
2
оценивают соответс-
твенно дисперсиями
и признают существенным при (σ
2
x
1
> 0, σ
2
x
2
> 0),
если соответственно окажется значимым отличие S
x
1
от S
x
1
x
2
и S
x
2
от S
2
x
1
x
2
, то есть если соответствующий
эмпирический критерий больше критического:
В том случае, когда одно из этих дисперсионных
отношений незначимо отличается от единицы, то есть
влияние одного из факторов несущественно (σ
2
x
1
= 0,
σ
2
x
2
= 0), для дисперсии σ
2
ε
+ m σ
2
x
1
x
2
получаются две од-
нородные оценки (соответственно S
x
1
и S
2
x
1
x
2
или S
x
2
и
S
2
x
1
x
2
), которые можно объединить в сводную оценку:
или

112
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
с большим числом степеней свободы
В том случае, когда оба дисперсионных отношения
незначимо отличаются от единицы, то есть влияние
обоих факторов несущественно (σ
2
x
1
= 0, σ
2
x
2
= 0), одно-
родные оценки S
x
1
, S
x
2
, S
2
x
1
x
2
для дисперсии σ
2
ε
+ mσ
2
x
1
x
2
можно объединить в сводную оценку:
с числом степеней свободы
2. Влияние взаимодействия факторов Х
1
X
2
с дис-
персией
признают существенным (σ
2
x
1
x
2
> 0), если отличие
S
2
x
1
x
2
и S
2
ε
окажется значимым, то есть если
В противном случае влияние взаимодействия счи-
тается несущественным (σ
2
x
1
x
2
= 0), и тогда обе одно-
родные оценки S
2
x
1
x
2
и S
2
ε
для σ
2
ε
можно объединить в
одну сводную оценку
с числом степеней свободы k
ε
= u
1
u
2
m – u
1
– u
2
+1.
В том случае, когда влияние и факторов X
1
и X
2
,
и их взаимодействия X
1
X
2
несущественно, дисперсию
воспроизводимости σ
2
ε
можно оценить выборочной об-
щей дисперсией S
2
0
.
Для практических вычислений сумм удобно поль-
зоваться их преобразованными выражениями:
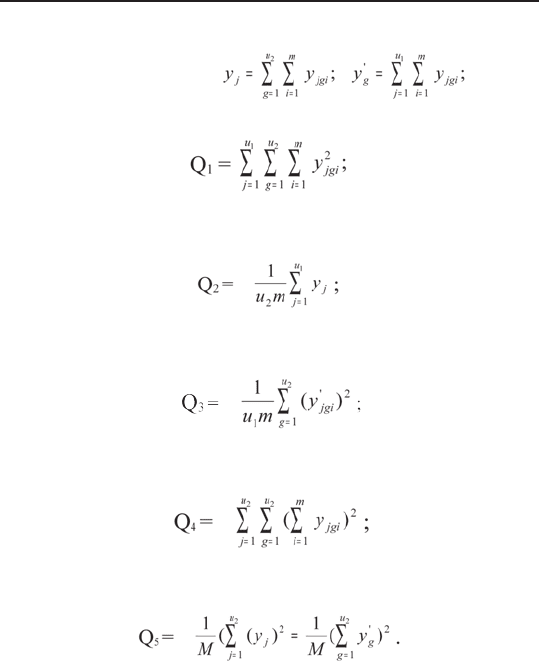
11
Математические методы и модели в экономике
— суммы наблюдений функции отклика y
j
по стро-
кам y’
g
и по столбцам
— сумма квадратов всех наблюдений
— сумма квадратов итогов (сумм) по строкам, де-
ленная на число наблюдений в строке,
— сумма квадратов итогов (сумм) по строкам, де-
ленная на число наблюдений в столбце,
— сумма квадратов итогов (сумм) по сериям, де-
ленная на число наблюдений в серии,
— квадрат общего итога (суммы), деленный на
число всех наблюдений,
При этом искомые суммы квадратов отклонений
определяются соотношениями:
S
0
= Q
1
- Q
5
; S
ε
= Q
1
– Q
4
; S
x
1
= Q
2
– Q
5
;
S
x
2
= Q
3
– Q
5
; S
2
x
1
x
2
= Q
4
+ Q
5
– Q
2
– Q
3.
При многофакторном анализе последовательность
операций аналогична, но значительно усложняются
таблицы наблюдений и расчетные формулы.

11
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
2.4.5. Кластерный анализ
Кластерный анализ представляет собой метод де-
ления статистической совокупности на части (группы,
классы, кластеры) одновременно по всем наиболее су-
щественным признакам.
В отличие от метода группировок, где на основе
предварительного теоретического анализа априорно
выделяются качественно своеобразные группы, оп-
ределяются для них (групп) наиболее существенные
черты (признаки), по которым производится класси-
фикация, кластерный анализ позволяет вначале по
определенным количественным критериям выделить
группы по комплексу признаков, а затем теоретичес-
ки обосновать качественное своеобразие выделенных
частей совокупности.
Наиболее существенным с методологической точки
зрения при кластерном анализе является следующее:
а) образование единой меры, охватывающей все при-
знаки;
б) чисто количественное определение границ групп.
Эти подходы находят отражение в следующем ал-
горитме классификации:
1. Пусть имеется 1, 2, ..., j, ..., т объектов, каждый
из которых характеризуется 1, 2, ..., i, ..., k признака-
ми. Тогда значение i-го признака по j-му объекту мож-
но записать как Х
ij
. Ставится задача провести класси-
фикацию единиц одновременно по всем k признакам.
2. Поскольку каждый из признаков имеет свою раз-
мерность и единицу измерения, признаки следует при-
вести в сопоставимый вид, что может быть сделано через
нормированное отклонение t
ij
. С этой целью следует:
•
найти х
i
, — среднее значение по каждому из k
признаков;
•
найти σ
i
, — среднее квадратическое отклонение
по каждому из k признаков;
•
пронормировать х
ij
как
11
Математические методы и модели в экономике
Осуществив переход от х
ij
к t
ij
, получим единицы,
свободные от содержания, имеющие с высокой степе-
нью надежности границы в пределах . С нормиро-
ванными отклонениями можно проводить любые ал-
гебраические операции, чего нельзя было делать с х
ij
.
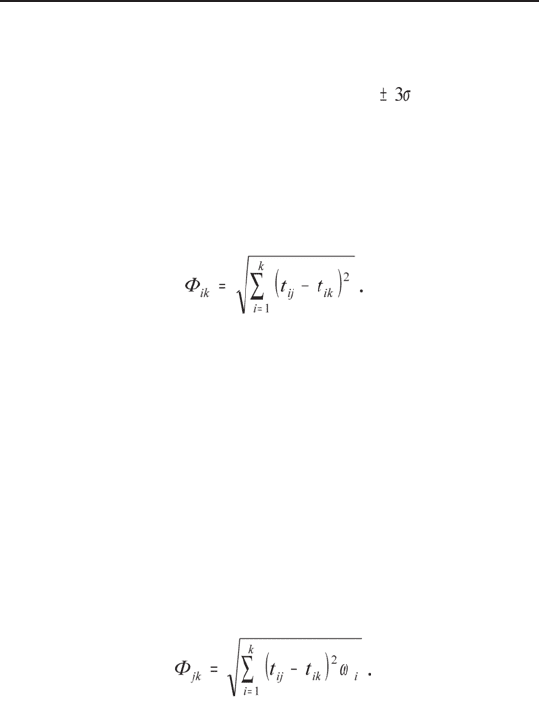
3. Выбирается функция состояния между объекта-
ми (единицами наблюдения). В качестве таковой мо-
жет выступать:
•
евклидово расстояние
Согласно этой формуле, вначале следует найти рас-
стояние между двумя объектами по одному признаку
(t
1j
-t
1p
), затем по другому (t
2j
-t
2p
) и т. д. Полученные
разности возводят в квадрат и суммируют, из полу-
ченной суммы извлекают квадратный корень;
• е-норма для k-го признака е
k
. Эту функцию на-
иболее часто используют, однако для определения
расстояния между объектами наблюдения можно при-
менять и другие методы. Важно учесть тот факт, что
при расчете функции расстояния по любому из ме-
тодов признакам может быть придан разный вес (ω).
Тогда функция расстояния, вычисленная, например,
как евклидово расстояние, будет иметь вид:
Определение веса (весового коэффициента ω
i
) для
каждого из признаков можно осуществлять на осно-
ве предварительного корреляционно-регрессионного
или факторного анализа, экспертных оценок и дру-
гих методов.
4. Если число классов (кластеров) известно зара-
нее, то устанавливаются типичные их представители,
то есть определяются значения признаков по типич-
ным представителям.
(2.85)
(2.86)

11
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
Если число кластеров заранее не задано и неизвес-
тны их типичные представители, то их число прини-
маем условно равным С. Каждый из объектов следует
отнести к тому из С-классов, с которым он имеет ми-
нимальную (по сравнению с другими классами) вели-
чину функции близости (расстояния).
Так как во втором случае число С неизвестно, оно
подбирается методом перебора. Этот метод включает:
•
определение функции расстояния каждого объек-
та с каждым (Ф
jk
);
•
установление порогового значения функции рас-
стояния (Ф
пор
);
•
объединение объектов в один кластер, когда рас-
стояние между ними меньше, чем пороговое. В ре-
зультате объединения получается некоторое число
кластеров, но часть объектов может остаться вне
кластеров;
•
нахождение центров тяжести по сформированным
кластерам;
•
определение функции близости между центрами
тяжести образованных кластеров, между центра-
ми тяжести и значением признаков по отдельным
объектам, между необъединенными объектами.
Принцип последующего объединения остается
прежним: объединение проводится при меньшем
значении функции расстояния, чем пороговое зна-
чение. Процесс объединения завершается, когда
все значения функции расстояния будут больше,
чем пороговое значение. Классификацию на осно-
ве перебора можно осуществить и без установле-
ния порогового значения. По такому алгоритму на
этом шаге итерации объединяются в один кластер
два (несколько) объекта, имеющие минимальную
величину функции расстояния. На втором шаге
находится центр тяжести по образованному клас-
теру и вновь определяются значения функции
расстояния. Объединяются объекты (кластеры) с
минимальным значением функции расстояния. На

11
Математические методы и модели в экономике
третьем и последующих шагах процесс объедине-
ния продолжается до тех пор, пока все объекты не
будут объединены в кластер.
На основе кластерного анализа может быть прове-
дена классификация как объектов, так и признаков. В
качестве функции расстояния в этом случае использу-
ется величина arccos r
lk
, где r
ik
— коэффициент парной
корреляции между признаками i и k. При r
ik
= 0 зна-
чение функции равно π/2, а при r
jk
= 1 — нулю. Про-
цесс осреднения признаков может быть осуществлен
по любому из описанных выше способов.

11
С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко
ГЛАВА 3
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
АНАЛИзА хОзяйСТВЕННОй
ДЕяТЕЛьНОСТИ
3.1. Измерение и оценка
хозяйственной деятельности
Практическая экономика независимо от микро-
или макросферы неизбежно сталкивается с задачей
измерения и оценки либо полученных результатов
хозяйственной деятельности, либо вариантов предсто-
ящей. Оценка базируется на измерении результатов
хозяйственной деятельности и использует некоторые
математические процедуры расчета этих результа-
тов. Методически и методологически составляющие
экономических показателей, выбираемых для изме-
рения эффекта (абсолютные показатели) или эффек-
тивности (относительные показатели) хозяйственной
деятельности, исследуются и разрабатываются такими
научными дисциплинами, как политическая экономия
и экономическая статистика. Однако инструменталь-
ные приемы расчета предоставляет математика.
Существуют два основных приема (подхода) к
оценке эффекта (эффективности) хозяйственной де-
ятельности: на основе использования системы показа-
телей и на основе использования одного показателя.
Если удается договориться об использовании од-
ного показателя, например, прибыли (эффект) или
рентабельности (эффективность), то, как правило,
при анализе результатов прошедшей деятельности
это позволяет однозначно определять, «успешно»
или «неуспешно» функционирует предприятие, а в
случае разработки планов ставить оптимизационные
задачи выбора наилучшего варианта при использо-

11
Математические методы и модели в экономике
вании выбранного показателя в качестве критерия
оптимальности.
Вместе с тем хозяйственная деятельность разно-
образна и многогранна, поэтому практически чаще
используют системы показателей, например таких,
как рентабельность, производительность труда, фон-
доотдача, материалоемкость и т. п. При использова-
нии системы показателей для анализа результатов
хозяйственной деятельности появляется возможность
выявить «узкие» места и выбрать направление основ-
ных усилий в предстоящей деятельности. Но при раз-
работке планов использование системы показателей
приводит к тупиковому результату, поскольку не поз-
воляет однозначно прийти к выводу о том, какой из
вариантов плана следует рассматривать как лучший.
В этом случае математика предлагает два основных
приема: свертывание системы показателей в единый
интегральный или использование «принципа опти-
мальности Парето».
Использование интегрального показателя, по су-
ществу, переводит ситуацию поликритериального
оценивания к ситуации монокритериального оцени-
вания и соответственно упрощает процесс принятия
управленческих решений.
Построение интегрального показателя осуществля-
ется либо в аддитивной, либо в мультипликативной
форме.
Аддитивная форма интегрального показателя име-
ет вид:
где I — интегральный показатель;
α
i
— весовые коэффициенты; весовые коэффициенты;
p
i
— нормированные, однонаправленные част-
ные показатели;
n — — количество показателей в используемой
системе.
(3.1)
