Грицюк С.Н., Мирзоева Е.В., Лысенко В.В. Математические методы и модели в экономике

Подождите немного. Документ загружается.

100

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Изучать влияние факторов по величинам их дис-

персий удобно, поскольку это простейшая мера рассе-

яния и к тому же аналогичная мере влияния фактора

случайных величин, то есть дисперсии единичного на-

блюдения (воспроизводимости) σ

. Благодаря этому

имеется возможность сравнивать влияние любого изу-

чаемого фактора и фактора случайности.

Исследование факторов по их дисперсиям называ-

ют дисперсионным анализом.

Дисперсионный анализ был предложен Р. Фише-

ром и развит А. Йейтсом.

Основная идея дисперсионного анализа заключает-

ся в разложении оценки общего рассеяния функции

отклика Y на составляющие, зависящие от:

•

случайных причин;

•

каждого из рассматриваемых факторов;

•

взаимодействия факторов;

•

оценивания статистической значимости диспер-

сий факторов с учетом ошибки воспроизводимости

опыта.

Техника дисперсионного анализа достаточно раз-

нообразна. Мы рассмотрим лишь простейшие способы,

наиболее часто встречающиеся в практике.

2.4.3. Однофакторный дисперсионный

анализ

Рассмотрим методику изучения влияния одного

фактора на целевую функцию Y по результатам т

наблюдений. Представим результаты экспериментов в

таблице 2.3.

Таблица 2.3

1 2 … I … m

1 y

… y

101

Математические методы и модели в экономике

2 y

… y

… … … … … … … …

j y

… y

… … … … … … … …

u Y

… Y

… y

Здесь j — порядковый номер уровня варьирования

фактора X (/ = 1, 2, ..., и); i — порядковый номер

параллельного опыта в серии на каждом у’-м уровне

(/ = 1, 2, ..., т). Для упрощения выкладок, не нару-

шая общности выводов, рассмотрим случай, когда на

всех уровнях число опытов т = const.

При расположении наблюдений в таблице их рас-

сеяние между столбцами обусловливается ошибкой

воспроизводимости, а рассеяние между строками —

дополнительным действием изучаемого фактора X.

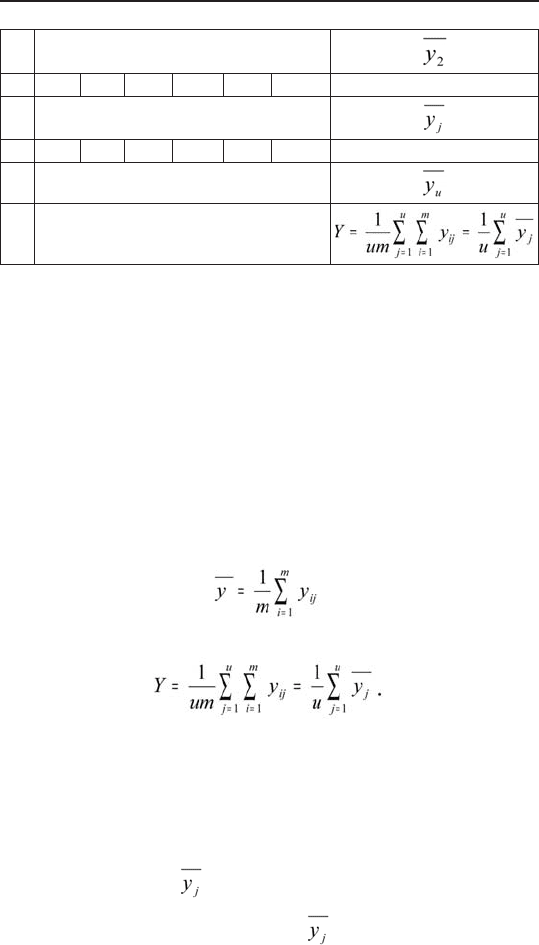
Вычислим средние арифметические для уровней:

и общее среднее по всем уровням:

Рассеяние отдельных наблюдений относительно об-

щего среднего обусловлено действием как случайных

причин, так и влиянием фактора X.

Действие фактора случайности проявляется в рас-

сеянии дисперсий σ

наблюдений серий параллель-

ных опытов у

на каждом уровне X

вокруг среднего

арифметического своей серии. Влияние же факто-

ра X с дисперсией σ

вызывает повышенное рассея-

ние средних арифметических серий относительно

102

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

общего среднего . Каждое из этих рассеяний можно

охарактеризовать соответствующей суммой квадратов

отклонений.

В соответствии с основной идеей дисперсионного

анализа разложим общую сумму квадратов отклоне-

ний наблюдений y

от общего среднего на две со-

ставляющие суммы, одна из которых характеризуется

влиянием фактора случайности, а вторая — влиянием

фактора изменчивости X:

Вследствие того, что

поскольку как сумма отклонений i-x

наблюдений j-й серии от среднего той же серии.

Суммы S

, S

и S

означают следующее:

— cумма

есть общая сумма квадратов отклонений отдельных

наблюдений у

от общего среднего . Она характеризу-

ет рассеяние наблюдений в результате действия обоих

факторов, как случайности Е, так и фактора X;

— сумма

есть сумма квадратов отклонений внутри серий, то

есть сумма квадратов разностей между отдельными на-

блюдениями y

, и средним соответствующей j-й се-

рии. Она характеризует остаточное рассеяние случайных

погрешностей опытов, то есть их воспроизводимости;

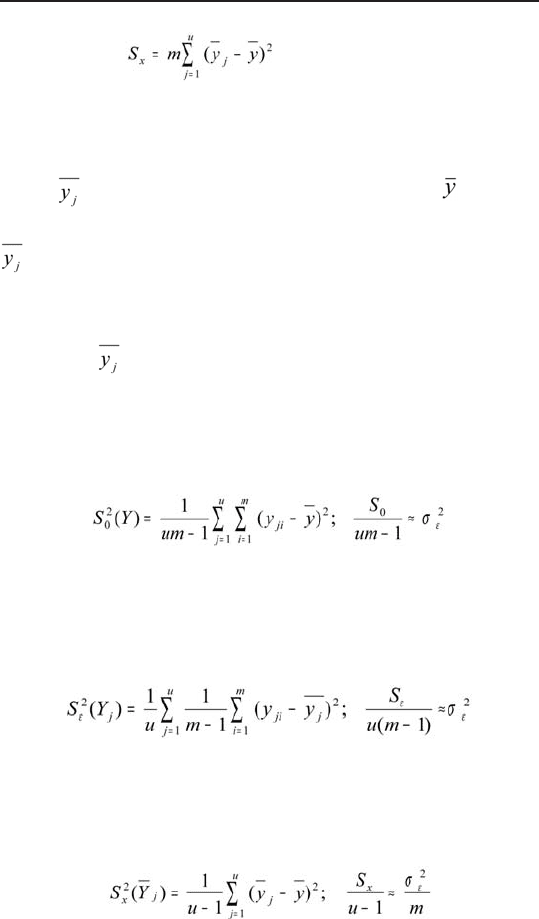
10

Математические методы и модели в экономике

— сумма

есть сумма квадратов отклонений между сериями

или рассеяние по уровням фактора X, то есть взве-

шенная с учетом числа т параллельных наблюдений в

каждой серии сумма квадратов разностей между сред-

ними отдельных серий и общим средним по всей

совокупности наблюдений.

Величина S

x /m

характеризует рассеяние средних

серий за счет случайных причин и исследуемого

фактора.

Предположим, что влияние фактора X на функцию

отклика Y отсутствует, то есть гипотеза H

об одно-

родности (j = 1, 2, 3, ..., и) верна. Тогда все и се-

рий наблюдений можно рассматривать как случайные

выборки из одной и той же нормальной генеральной

совокупности U. Следовательно:

— несмещенная общая оценка дисперсии воспроиз-

водимости σ

по всем ит наблюдениям

с числом степеней свободы k

= ит – 1;

— выборочная дисперсия рассеяния внутри отде-

льных серий, или остаточная оценка дисперсии вос-

производимости σ

, находится как среднее из выбо-

рочных дисперсий по каждой серии в отдельности:

с числом степеней свободы k

= и(т – 1);

— выборочная дисперсия средних по сериям слу-

жит несмещенной оценкой дисперсии σ

/т, с которой

нормально распределены независимо друг от друга

средние j-х серий:

и – 17 = 1 и – 1 = т

10

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

с числом степеней свободы k

= и – 1. При этом

= k

+ k

;

В результате более глубокого анализа можно пока-

зать, что S

и S

независимы друг от друга.

Из сказанного очевидно, что при отсутствии вли-

яния фактора X оценки S

, S

и S

однородны, так

как являются оценками одной и той же генеральной

дисперсии G.

Теперь предположим, что влияние фактора Х на

отклик существенно, то есть гипотеза H

об однород-

ности неверна. Тогда и серий параллельных наблю-

дений можно рассматривать как случайные выборки и

независимых нормально распределенных случайных

величин с одной и той же дисперсией σ

и различны-

ми генеральными центрами распределения С

, С

, ...,

, ..., С

. Следовательно:

— выборочная дисперсия S

характеризует влияние

как фактора случайности, так и фактора X, то есть

— так как сумма S

не изменяется при замене у

на (y

– C

), где Cj — генеральный центр распреде-

ления целевой функции Y при стабилизации фактора

X на j-м уровне, то выборочная дисперсия S

также

не изменяется и по-прежнему является несмещенной

оценкой для генеральной дисперсии воспроизводимос-

ти σ

, то есть

— поскольку сумма S

учитывает не только случай-

ные, но и систематические расхождения между сред-

ними серий и увеличивается за счет влияния фактора

X, дисперсия S

при этом также увеличивается и

перестает служить оценкой только для σ

/т, то есть

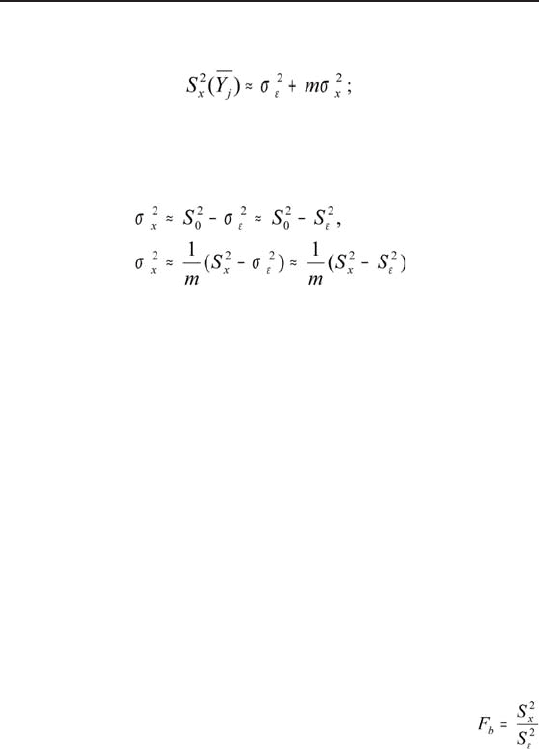
10

Математические методы и модели в экономике

откуда следует, что

— независимость S

и S

друг от друга сохраняется.

Таким образом, для дисперсии фактора X теперь мож-

но дать две оценки:

Первая оценка менее точна из-за погрешностей

влияния S

и S

. Точность же второй выше, так

как выборочные дисперсии входят в нее поделен-

ными на т.

Из сделанного второго предположения очевидно,

что при влиянии фактора X оценки S

, S

неод-

нородны. Следовательно, сопоставляя эти выборочные

дисперсии, можно принять решение о справедливости

первого и второго предположений относительно су-

щественности влияния фактора X (с дисперсией σ

)

на функцию отклика Y. Учитывая точность выраже-

ний для σ

, для проверки гипотезы H

: σ

= 0 будем

сравнивать выборочные дисперсии S

и S

Для того чтобы влияние фактора X было признано

существенным, то есть принята гипотеза H

: σ

≠ 0,

необходимо и достаточно, чтобы оценка дисперсии S

значимо отличалась от S

. Здесь используется крите-

рий Фишера, для чего определяется статистика

и при принятом уровне значимости а и числе степеней

свободы k

и k

сравнивается с критическим значением

α;

При F

≤ F

α;

принимается гипотеза о незави-

симости σ

, то есть верна гипотеза H

: σ

= 0.

Следует иметь в виду, что дисперсионный анализ

результатов эксперимента позволяет оценивать вли-

яние фактора X лишь в целом и что выводы, полу-

ченные с его помощью, относятся только к данному

10

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

эксперименту при выбранной систематизации полу-

ченных результатов. Но может случиться так, что при

изменении диапазона варьирования изучаемого фак-

тора или основной (базовой) точки оценки влияние

последнего может измениться.

Если принимается гипотеза H

: σ

= 0, то диспер-

сию воспроизводимости σ

можно оценить выбороч-

ной общей дисперсией S

, которая имеет на (u – 1)

степеней свободы больше, чем S

. Если же принима-

ется гипотеза Н

. σ

≠ 0, то дисперсия воспроизводи-

мости σ

оценивается остаточной дисперсией

а доверительный интервал для σ

можно опреде-

лить по χ

— распределению (хи-квадрат) с и(т – 1)

степенями свободы;

— дисперсия фактора X

— расхождение центров серий δ

, обусловленное

влиянием фактора X, определяется следующим обра-

зом. Так как

то можно показать, что

где — среднее значение из центров рас-

пределения С

или

Оценкой величины δ

служит выборочная харак-

теристика

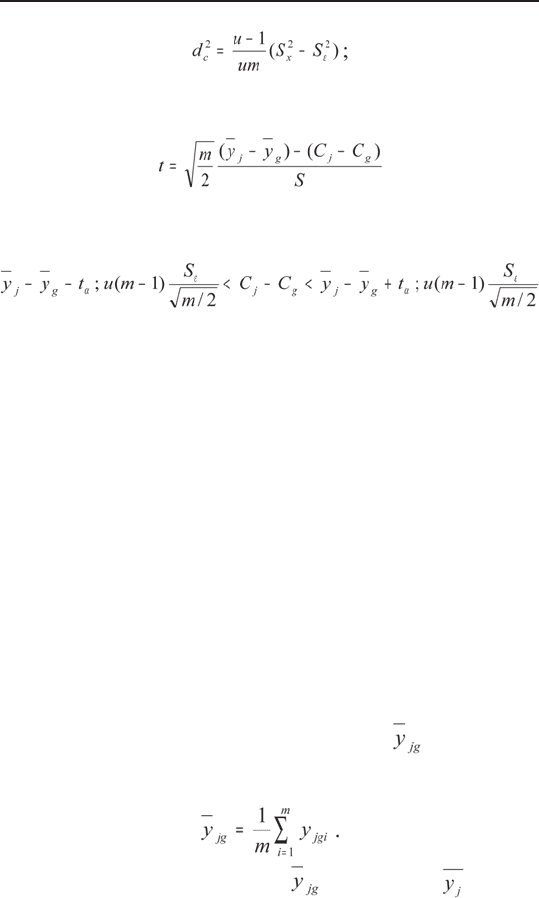
10

Математические методы и модели в экономике

— расхождение (С

– C

) между центрами любых

серий также может быть оценено. Так как статистика

следует распределению Стьюдента с числом степе-

ней свободы k = и(т-1), то интервал

служит доверительным интервалом (1 – α) для рас-

хождения (Cj – C

2.4.4. Двухфакторный дисперсионный

анализ

Пусть изучается влияние двух одновременно дейс-

твующих факторов Х

и Х

. Представим в таблице ре-

зультаты эксперимента из u

m наблюдений y

jgi

, где

j — порядковый номер уровня варьирования фактора

(j = 1, 2, ..., u

); g

порядковый номер уровня ва-

рьирования фактора Х

(g = 1, 2, ..., u

); i — порядко-

вый номер параллельного опыта в серии при каждом

jg-ы сочетании уровней факторов Х

и Х

(i = 1, 2

... m

). Для упрощения выкладок рассмотрим случай

равночисленных серий наблюдений при всех возмож-

ных сочетаниях уровней, то есть m

= m = const.

Вычислим средние арифметические серий из т

повторных наблюдений для каждого сочетания j-го и

g-го уровней факторов Х

и Х

Средние арифметические по строкам из и

наблюдений для каждого j-го уровня фактора Х

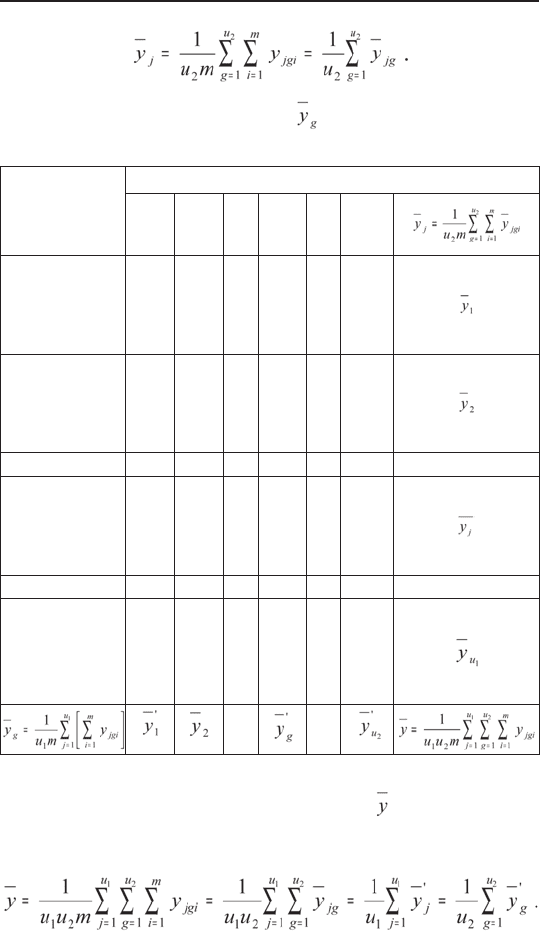
10

С. Н. Грицюк, Е. В. Мирзоева, В. В. Лысенко

Средние арифметические по столбцам из u

наблюдений для каждого g-ro уровня фактора Х

Номер

j-го уровня-го уровня

фактора Х

Номер j-го уровня фактора Хj-го уровня фактора Х-го уровня фактора Х

1 2 … g … u

111

121

… y

1g1

… y

112

122

… y

1g2

… y

… … … … … …

21m

12m

… y

1gm

… y

211

221

… y

2g1

… y

212

222

… Y

2g2

… y

… … … … … …

21m

22m

… y

2gm

… y

… .. … … … … … …

j11

j21

… y

jg1

… y

j12

j22

… y

jg2

… y

… … … … … …

j1m

j2m

… y

jgm

… y

… .. … … … … … …

… y

… … … … … …

… y

… …

Общая средняя арифметическая для всех М =

= u

m наблюдений по всем u

сочетаниям

уровней:

10

Математические методы и модели в экономике

При указанном расположении наблюдений их рассе-

яние в каждой серии относительно среднего той же се-

рии обусловлено действием только случайных причин

с дисперсией σ

. Рассеяние же самих средних в сериях

по всем возможным сочетаниям уровней варьирова-

ния факторов Х

и Х

вокруг общего среднего помимо

фактора случайности вызывается влиянием фактора

взаимодействия X

с дисперсией σ

. Кроме этих

факторов на рассеяние средних по строкам оказывает

влияние только один фактор Х

с дисперсией σ

, а на

рассеяние средних по столбцам — только один фактор

с дисперсией σ

, так как все уровни другого фак-

тора в каждом из этих случаев осреднены.

В соответствии с основной идеей дисперсионного

анализа разложим общую сумму S

квадратов откло-

нений наблюдений от общего среднего на компоненты,

отвечающие перечисленным выше факторам:

В выражении величина

— общая сумма квадратов, характеризующая рас-

сеяние отдельных наблюдений y

jgi

в общей совокупнос-

ти за счет влияния всех факторов.

Величина

— сумма квадратов отклонений внутри серий, харак-

теризующая рассеяние отдельных наблюдений y

jgi

в се-

риях только за счет влияния фактора случайности, так

как на протяжении серии факторы Х

и Х

остаются не-

изменными.

Величина