Giga Y. Surface Evolution Equations: A Level Set Approach

Подождите немного. Документ загружается.

68 Chapter 1. Surface evolution equations

nonlinear parabolic equations (including higher order equations) is well developed

in a book by A. Lunardi (1995) improving the theory of O. A. Ladyˇzehnskaya, V.

A. Solonnikov and N. N. Ural´ceva (1968).

A general result of Y. Giga and S. Goto (1992b) yields the unique local

existence of a smooth solution for (1.5.4) for arbitrary smooth initial data but for

(1.5.9), (1.5.10) with m>1, (1.5.12), (1.5.14), V = K

for strict convex smooth

initial data so that the equation is strictly parabolic. If (1.5.2) is strictly parabolic

and γ and β are smooth enough, the same result for (1.5.4) holds. However, if

there is degeneration of parabolicity in (1.5.2) with a>0, we do not expect to

have a smooth solution even locally-in-time for arbitrary smooth initial data, as

observed by Y. Giga (1994). For the ﬁrst order equation like (1.5.6) one can prove

the unique local existence of a smooth solution for arbitrary smooth initial data

by a method of characteristics.

There is a general theory of local solvability by A. Polden (See an article by

G. Huisken and A. Polden (1999)) for strictly parabolic equation (1.5.1) including

higher order equations.

We conclude this section by pointing out that there is a nice review article by

M. Struwe (1996) on evolution equations related to geometry including the mean

curvature ﬂow equations as well as the harmonic map ﬂow equations. This article

explains singularities and weak solutions. It contains a short introduction to the

level set method as well.

Chapter 2

Viscosity solutions

The level set equations we would like to study are parabolic, but they are very

degenerate. The classical techniques and results cannot be expected to apply. For

example the initital value problem for degenerate parabolic equations may not

admit a smooth solution for smooth initial data even locally in time. Moreover,

level set equations may be singular at a place where the spatial gradient of solu-

tions vanishes as noted for the level set mean curvature ﬂow equations. Even for

such singular degenerate equations it turns out that the theory of viscosity solu-

tions provides a correct notion of generalized solutions. In this chapter we shall

present the basic aspect of the theory especially for singular degenerate parabolic

equations.

2.1 Deﬁnitions and main expected properties

To motivate the deﬁnition of a viscosity solution we consider a C

function u =

u(z) which satisﬁes a diﬀerential inequality:

(z)+F (z, u(z), ∇u(z), ∇

u(z)) ≤ 0(2.1.1)

for all z =(x, t)inΩ× (0,T), where Ω is a domain in R

and T>0, and F is a

function in Ω × R × R

× S

. We assume that F is (degenerate) elliptic , i.e.,

F (z, r,p, X) ≤ F (z, r,p,Y )forX ≥ Y,

so that the equation

+ F (z,u,∇u, ∇

u)=0 (2.1.2)

is a parabolic equation. Suppose that ϕ is also C

and u−ϕ takes its local maximum

at ˆz =(ˆx,

t)withˆz ∈ Ω × (0,T). Then the classical maximum principle which is

just calculus implies that

(ˆz)=ϕ

(ˆz), ∇u(ˆz)=∇ϕ(ˆz), ∇

u(ˆz) ≤∇

ϕ(ˆz).

70 Chapter 2. Viscosity solutions

The degenerate ellipticity together with (2.1.1) implies that

(ˆz)+F (ˆz,u(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz))

≤ u

(ˆz)+F (ˆz,u(ˆz), ∇u(ˆz), ∇

u(ˆz)) ≤ 0.

The same inequality for ϕ is obtained even if Ω × (0,T) is replaced by Ω × (0,T]

so that

t may equal T , since we still have

(ˆz) ≤ ϕ

(ˆz)

although u

(ˆz)maynotequalϕ

(ˆz). The inequality

(ˆz)+F (ˆz, u(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0(2.1.3)

does not include derivatives of u so we are tempted to deﬁne an arbitrary function

u to be a generalized subsolution of (2.1.2) in Ω × (0,T)ifforeachˆz ∈ Ω × (0,T)

an upper test function ϕ of u around ˆz always solves (2.1.3). There are a couple

of degrees of freedom to deﬁne viscosity solutions when F is not continuous. One

should take a good deﬁnition of solutions which enjoy major expected proper-

ties including comparison principle, stability principle and Perron’s construction

of solutions. We shall give such deﬁnitions for a typical class of equations. For

technical convenience we deﬁne a notion of solutions for arbitrary discontinuous

functions.

2.1.1 Deﬁnition for arbitrary functions

To handle arbitrary functions we recall the upper and lower semicontinuous enve-

lope deﬁned in §1.6.5. Let h be a function deﬁned on a set L of a metric space X

with values in R ∪{±∞}.Theupper semicontinuous envelope h

∗

and the lower

semicontinuous envelope h

∗

of h are deﬁned by

∗

(z) = lim

r↓0

sup{h(ζ); ζ ∈ B

(z) ∩ L}

∗

(z) = lim

r↓0

inf{h(ζ); ζ ∈ B

(z) ∩ L}

z ∈

L (2.1.4)

respectively, as functions deﬁned on the closure

L of L with values in R

∪

{±∞},

where B

(z) is a closed ball of radius r centered at z in X.Inotherwordsh

∗

the greatest lower semicontinuous function on

L which is smaller than h on L and

similarly, h

∗

is the smallest upper semicontinuous function on L which is greater

than h on L. Clearly h

∗

= h if h is lower semicontinuous in L and h

∗

= h if h is

upper semicontinuous in L. (We recall here that a function f on Z ⊂ X is said to

be lower semicontinuous if

lim inf

x→z

f(x) ≥ f (z) for all z ∈ Z.

This condition is equivalent to saying that any super level set

{z ∈ Z; f(z) >α} (α ∈ R)

2.1. Deﬁnitions and main expected properties 71

is open. If −f is lower semicontinuous, f is said to be upper semicontinuous .)

For continuous ϕ on

L it is clear that (h − ϕ)

∗

= h

∗

− ϕ. Also by deﬁnition

∗

= −(−h)

∗

.Forh

∗

the maximum over compact set K is always attained provided

that h

∗

(z) < ∞ for z ∈ K. This property is often used in the sequel.

()yhz

()

Figure 2.1: Upper semicontinuous envelope

We ﬁrst give a rigorous deﬁnition of a solution of (2.1.2) when F has no

singularities.

Deﬁnition 2.1.1. Let Ω be an open set in R

and T>0. Let F be a continuous

function on

Ω × [0,T] × R × R

× S

with values in R.LetO be an open set in

Ω × (0,T).

(i) A function u : O→R ∪{−∞}is a (viscosity) subsolution of

+ F (z,u,∇u, ∇

u)=0 (2.1.5)

in O (or equivalently, solution of u

+ F (z,u,∇u, ∇

u) ≤ 0) if

(a) u

∗

(z) < ∞ for z ∈O.

(b) If (ϕ, ˆz) ∈ C

(O) ×O satisﬁes

max

∗

− ϕ)=(u

∗

− ϕ)(ˆz), (2.1.6)

then

(ˆz)+F (ˆz,u

∗

(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0. (2.1.7)

(ii) A function u : O→R ∪{+∞} is a (viscosity) supersolution of (2.1.5) in O

(or equivalently, solution of u

+ F (z,u,∇u, ∇

u) ≥ 0) if

(a) u

∗

(z) > −∞ for z ∈O.

(b) If (ϕ, ˆz) ∈ C

(O) ×O satisﬁes

min

∗

− ϕ)=(u

∗

− ϕ)(ˆz), (2.1.8)

then

(ˆz)+F (ˆz,u

∗

(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≥ 0. (2.1.9)

72 Chapter 2. Viscosity solutions

By deﬁnition this is equivalent to saying that v = −u is a solution of

− F (z,−v, −∇v, −∇

v) ≤ 0.

We shall often supress the word “viscosity”. In every circumstance when sub-

and supersolutions are deﬁned, we say a function is a (viscosity) solution of the

equation in a given set if it is both a sub- and supersolution of the equation in

the set. A function ϕ satisfying (2.1.6) is called an upper test function of u at ˆz

over O and ϕ satisfying (2.1.8) is called a lower test function of u at ˆz over O.As

observed from (2.1.3) the notion of viscosity solutions is a natural extension of the

notion of solutions if F is degenerate elliptic.



Figure 2.2: Upper test function

Proposition 2.1.2. Assume that u ∈ C

(O) (i.e., u is C

on O). Assume that F

is degenerate elliptic. Then u is a subsolution (resp. supersolution) of (2.1.5) in O

if and only if u satisﬁes

+ F (z,u,∇u, ∇

u) ≤ 0(resp. ≥ 0)

in O.

Remark 2.1.3. It is sometimes convenient to deﬁne solutions in an open set O in

Ω × (0,T] instead of Ω × (0,T). It is deﬁned in the same way as in Deﬁnition 2.1.1.

As remarked before (2.1.3), the statement of Proposition 2.1.2 is still valid even if

O intersects t = T .

The notation of viscosity solutions can be localized.

Localization property.

(i) If u is a subsolution of an equation in a neighborhood of each point of Ω ×

(0,T), then it is a subsolution (of the same equation) in Ω × (0,T).

2.1. Deﬁnitions and main expected properties 73

(ii) If u is a subsolution (of an equation) in Ω × (0,T), then it is a subsolution

(of the same equation) in every open set O in Ω × (0,T).

(iii) The properties (i), (ii) are still valid if a supersolution replaces a subsolution.

This is easily proved for equation (2.1.5) by restricting and extending test

functions.

Unfortunately, if (2.1.5) is a level set equation, the value of F at ∇u =0may

not be deﬁned. We have to extend the deﬁnition of viscosity solutions for (2.1.5)

with discontinuous F to handle such equations.

Deﬁnition 2.1.4. (i) Assume that F is lower semicontinuous in W =

Ω × [0,T] ×

R × R

× S

with values in R ∪{−∞}. A subsolution of (2.1.5) is deﬁned as in

Deﬁnition 2.1.1 (i).

(ii) Assume that F is upper semicontinuous in W with values in R ∪{+∞}.

A supersolution of (2.1.5) is deﬁned as in Deﬁnition 2.1.1 (ii). Here we use the

convention that a + ∞ = ∞ > 0anda −∞= −∞ < 0 for any real number a.

(iii) Assume that F is deﬁned only in a dense subset of W and that F

∗

< ∞,

∗

> −∞ in W .Ifu is a subsolution of

+ F

∗

(z,u,∇u, ∇

u)=0

in O,thenu is called a subsolution of (2.1.5) in O.Ifu is a supersolution of

+ F

∗

(z,u,∇u, ∇

u)=0

in O,thenu is called a supersolution of (2.1.5). (In applications the case when F

is continuous in

Ω × [0,T] × R × (R

\{0}) × S

has a particular importance.)

As stated for continuous F , the statement of Proposition 2.1.2 and the local-

ization property are still valid for such an F .

2.1.2 Expected properties of solutions

We shall explain in an informal way three major properties which viscosity solu-

tions are expected to satisfy.

Comparison principle. If u is a subsolution of (2.1.5) in Q =Ω× [0,T) and v

is a supersolution of (2.1.5) in Q,thenu

∗

≤ v

∗

in Q if u

∗

≤ v

∗

on the parabolic

boundary ∂

Q of Q, i.e.,

∂

Q =Ω×{0}∪∂Ω × [0,T).

This is a comparison principle for semicontinuous functions so it is sometimes

called a strong comparison principle to distinguish the comparison principle for

continuous functions.

74 Chapter 2. Viscosity solutions

The major structural assumptions to guarantee the comparison principle are

degenerate ellipticity of F and monotonicity of F = F (z,r,p, X)inr in the sense

that

r → F (z,r,p,X)

is nondecreasing. The last property can be weakened to the nondecreasing property

r → F (z,r,p,X)+c

for some c

independent of (z,p,X). (Indeed, by the change of variable u by e

this condition yields the stronger version of the monotonicity condition for the

equation for v.) We need other regularity assumptions for F . A simplest set of

assumptions for continuous F is that F is independent of z, r and is degenerate

elliptic. In this case as we will see later the comparison principle holds at least

for bounded Ω. (For unbounded Ω one should modify the interpretation of the

inequality u

∗

≤ v

∗

If F = F (z,r,p,X) has a singularity (discontinuity) at p = 0 (but is contin-

uous elsewhere), we assume that

−∞ <F

∗

(z,r,0,O)=F

∗

(z,r,0,O) < ∞ (2.1.10)

to get the comparison principle. (In Chapter 1 we have characterized a class of op-

erators F

(p, X) such that this condition is fulﬁlled. See Lemma 1.6.16–Proposition

1.6.18. Many geometric F in level set equations including mean curvature ﬂow

equations (1.5.4) fulﬁll this condition.) This assumption cannot be removed com-

pletely.

Counterexample. We set F (p, X)=−X/|p|

with N =1,α > 0. Then both

u ≡ 0and

v(x, t)=



1 t ≥ T,

0 t<T

are solutions of (2.1.5) in R × (0, ∞). Of course F is degenerate elliptic but it

violates (2.1.10); indeed

∗

(0,O)=−∞,F

∗

(0,O)=+∞.

Since both u and v are initially zero, the comparison principle is violated. One

complaint lies in the fact that R is unbounded. But it still gives a counterexample

for the comparison principle which is expected to hold for an unbounded domain.

We do not pursue a counterexample for a bounded domain.

Stability principle. We begin with its naive form. Assume that F

converges to F

locally uniformly (as ε → 0 with ε>0) in the domain of deﬁnition of F . Assume

that u

solves

εt

+ F

(z,u

, ∇u

, ∇

) ≤ 0 (resp. ≥ 0)inO

2.1. Deﬁnitions and main expected properties 75

and that u

converges to u locally uniformly (as ε → 0)inO.Thenu solves

+ F (z,u,∇u, ∇

u) ≤ 0(resp.≥ 0) in O.

This property is useful when we want to construct a solution u of (2.1.5)

by approximating the equation. There are several options to weaken the assump-

tion of convergences F

→ F , u

→ u. We may replace “convergence” by “semi-

convergence”. Let h

be a function deﬁned on a set L of a metric space X with

values in R ∪{±∞},whereε>0. The upper relaxed limit

h = lim sup

∗

and the

lower relaxed limit h

= lim inf

∗

are deﬁned by

h(z) = (lim sup

ε→0

∗

)(z) = lim sup

ζ→z

ε→0

(ζ)

= lim

ε→0

sup{h

(ζ); ζ ∈ L ∩ B

(z), 0 <δ<ε},

(z) = (lim inf

ε→0

∗

)(z) = lim inf

ζ→z

ε→0

(ζ)

= lim

ε→0

inf{h

(ζ); ζ ∈ L ∩ B

(z), 0 <δ<ε},

respectively. These limits are a kind of ‘lim sup’ and ‘lim inf’ but take such an

operation in both ε and ζ. The functions lim sup

∗

and lim inf

∗

are deﬁned for

all z in

L allowing the values ±∞.Evidently,ifh

= h,then

∗

= lim sup

∗

and h

∗

= lim inf

∗

By deﬁnition

h = lim sup

∗

)andh = lim inf

∗

)

∗

.Ifwesetk(z,ε)=h

(z)as

a function of z ∈ L and ε>0, then by deﬁnition

h(z)=k

∗

(z,0),h(z)=k

∗

(z,0) for z ∈ L.

h = h on L,thenk

∗

and k

∗

are continuous at ε = 0 as functions in L × (0, 1).

This implies that h

converges to h = h locally uniformly in L as ε → 0.

The convergence u

→ u may be replaced by semi-convergence u = u if we

consider sequences of subsolutions. For sequences of supersolutions we may replace

→ u by u = u. The convergence F

→ F is replaced by F ≤ F and F ≥ F for

sub and supersolutions respectively. If convergence is replaced by semi-convergence

in the stability principle, it is sometimes called the strong stability principle. The

major advantage lies in the fact that

u and u always exist allowing the values ±∞.

So to apply the strong stability principle we need not estimate {u

} to get locally

uniform convergence of u

.Onceweprove(−∞ <) u ≤ u (< ∞) for example by

the comparison principle, we have

u = u. This implies a posteriori locally uniform

convergence u

→ u = u = u and the limit u is continuous.

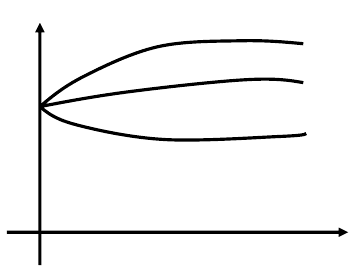
Perron’s method (Construction of solutions). If u

and u

−

are super- and sub-

solution of (2.1.5) in Ω × [0,T), respectively, then there is a solution u of (2.1.5)

76 Chapter 2. Viscosity solutions





Figure 2.3: Perron’s method

in Ω × [0,T) that satisﬁes u

−

≤ u ≤ u

on Ω × (0,T) provided that u

−

≤ u

Ω × (0,T).

This method reduces the business of construction of solutions to ﬁnding ap-

propriate sub- and supersolutions satisfying the initial and boundary conditions.

For example consider the initial value problem for (2.1.5) with continuous initial

data u

,whereΩ=R

. If there are sub- and supersolutions u

of (2.1.5) in

× (0,T)thatsatisfy

+∗

(x, 0) = u

(x)=u

−

∗

(x, 0),

then by Perron’s method we have a solution u. Moreover, if the comparison prin-

ciple applies, then u

∗

≤ u

∗

in R

× [0,T). This implies that u is continuous on

× [0,T)withu(0,x)=u

(x). The uniqueness of such a solution is clear from

the comparison principle. Since R

is unbounded, the comparison principle is not

exactly as stated above, this discussion is a little bit informal but it explains the

basic idea to get a solution.

Apparently, Deﬁnition 2.1.4 is a natural extension for discontinuous F .In-

deed the deﬁnition for continuous F is included. Moreover, the stability principle

and Perron’s method is available. If (2.1.10) is fulﬁlled, as we see later, the compar-

ison principle holds under reasonable regularity assumptions on F at least when

F (z, r,p, X) is continuous outside p = 0. This class of equations includes many im-

portant examples of level set equations satisfying (1.6.24) so for example it applies

to the level set mean curvature ﬂow equation (1.6.5). However, for the level set

equation of the Gaussian curvature ﬂow (1.6.12), condition (2.1.10) is not fulﬁlled

(see §1.6.5). If F fails to satisfy (2.1.10), the comparison principle may not hold.

One should modify the notion of viscosity solutions for such problems as discussed

in the next subsection.

In this chapter we only discuss the stability principle and Perron’s method.

We discuss the comparison principle in the next chapter.

2.1. Deﬁnitions and main expected properties 77

2.1.3 Very singular equations

Let F be continuous on W

= Ω×[0,T]×R×(R

\{0})×S

with values in R.We

restrict the test functions. Let F

Ω

= F

Ω

(F ) be the set of functions f ∈ C

[0, ∞)

such that

f(0) = f



(0) = f



(0) = 0 and f



(r) > 0forr>0

and that for s = ±1,

lim

p→0

sup

z∈O

sup

r∈R

|F (z, r,∇

(f(|p|)),s∇

(f(|p|)))| =0. (2.1.11)

The formula (2.1.11) is often written as

lim

p→0

sup

z∈O

sup

r∈R

|F (z, r,∇(f|p|)), ±∇

(f(|p|))| =0.

We suppress the Ω-dependence of F in this chapter since we ﬁx Ω. We say that

ϕ ∈ C

(O)iscompatible with F if for any ˆz =(ˆx,

t)inO with ∇ϕ(ˆz)=0,there

is a constant δ>0 and functions f ∈F and ω

∈ C[0, ∞) with lim

σ→0

(σ)/σ =0

that satisﬁes

|ϕ(x, t) − ϕ(ˆz) − ϕ

(ˆz)(t −

t)|≤f(|x − ˆx|)+ω

(|t −

t|)(2.1.12)

for all (x, t) ∈Owith |x − ˆx|≤δ, |t −

t|≤δ.Thesetofϕ ∈ C

(O) compatible

with F is denoted by C

(O).

Note that the set F can be empty. Indeed, for N =1let

F = F (p, X)=−X/|p|

. (2.1.13)

If α ≥ 1, then, by the Gronwall inequality for f



, a function f ∈ C

[0, ∞)that

satisﬁes

lim

x→0



α

=0 with f



≥ 0,f



(0) = 0,

is a constant near x = 0. This violates f



(σ) > 0forσ>0sothesetF is empty for

α ≥ 1. If 0 <α<1, f(σ)=σ

belongs to F provided that γ>(2 − α)/(1 − α).

The case α ≥ 1, the initial value problem for (2.1.5) with (2.1.13), cannot be

expected to be solvable except for monotone initial data. The case 0 <α<1, the

equation (2.1.5) with (2.1.13), is the q-Laplace diﬀusion equation (with 1 <q<2)

− c div(|∇u|

q−2

∇u)=0, (2.1.14)

where q =2− α, c =1/(q − 1),N=1.IfF = F(p, X) is geometric, degenerate

elliptic and continuous outside p = 0, then it turns out that F is not empty. We

shall discuss this point in the next chapter. It is easy to see that F is invariant