Giga Y. Surface Evolution Equations: A Level Set Approach

Подождите немного. Документ загружается.

88 Chapter 2. Viscosity solutions

for (x, t) suﬃciently close to (ˆx,

t). If we set

(x, t)=ϕ − Φ+θ

(|x − ˆx|)+θ

(|t −

t|)+|x − ˆx|

+ |t −

then ψ

is a separable function

(x, t)= b(x)+g(t),

b(x)= ∇ϕ(ˆx,

t),x− ˆx +

∇

ϕ(ˆx,

t)(x − ˆx),x− ˆx

+θ

(|x − ˆx|)+|x − ˆx|

g(t)= ϕ

(ˆx,

t)(t −

t)+θ

(|t −

t|)+|t −

and b ∈ C

),g∈ C

(R). Since ϕ<ψ

near (ˆx,

t) (except (ˆx,

t)) and ϕ(ˆx,

t)=

(ˆx,

t), u

∗

−ψ

takes its local strict maximum at ˆz =(ˆx,

t)with∇ϕ(ˆx,

t)=∇b(ˆx),

∇

ϕ(ˆx,

t)=∇

b(ˆx), ϕ

(ˆx,

t)=g



(

t).

We approximate b by a smooth function b

so that b

converges to b locally

uniformly together with its derivatives up to second order (as ε → 0). We approx-

imate g by a smooth function so that g

→ g locally uniformly with its derivative.

We now apply Lemma 2.2.5 or its simpler version Remark 2.2.6 (i) to u

∗

− b

− g

with X = O,S = {ˆz} to get that there is a sequence z

=(x

)convergingtoˆz

such that

∗

− b

− g

≤ (u

∗

− b

− g

)(z

)nearz

, (2.2.8)

lim

n→∞

∗

− b

− g

)(z

)=(u

∗

− b − g)(ˆz). (2.2.9)

Since b

→ b, g

→ g uniformly (together with its derivatives), we get

⎧

⎨

⎩

) → b(ˆx),g

) → g(

t),

∇b

) →∇b(ˆx),g



) → g



(

t),

∇

) →∇

b(ˆx)withz

=(x

(2.2.10)

By (2.2.9) this implies

∗

) → u

∗

(ˆz). (2.2.11)

Since (2.2.8) holds, we apply (2.1.7) at z

to get



)+F (z

∗

), ∇b

), ∇

)) ≤ 0. (2.2.12)

Since F is lower semicontinuous, sending ε to 0 yields, by (2.2.10) and (2.2.11),



(

t)+F (ˆz, u

∗

(ˆz), ∇b(ˆx), ∇

b(ˆx)) ≤ 0,

which is

(

t)+F (ˆz, u

∗

(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0.

This is what we want to prove. The proof for supersolutions is similar so is omitted.

It remains to study whether test functions in Deﬁnition 2.1.5 may be replaced

by A

(O). It suﬃces to prove ϕ

(ˆz) ≤ 0forϕ ∈ C

(O) satisfying (2.1.6) when

∇ϕ(ˆz) = 0 by assuming that diﬀerential inequalities in Deﬁnition 2.1.5 hold for

2.2. Stability results 89

all z ∈Oand all ψ ∈∩

∞

k=1

(O) such that u

∗

− ψ takes a local maximum at z.

The basic idea of the proof is the same as above. We take ψ

= ψ as deﬁned in

(2.2.7) and observe that u

∗

− ψ

takes a strict local maximum at ˆz and that ψ

of form

(x, t)=f(|x − ˆx|)+g(t)

with some f ∈F and g ∈ C

(R) (Note that af ∈F,a > 0). We approximate g

by g

∈ C

∞

(R) as before. (Approximation of f ∈F by f

∈ C

∞

(0, ∞) ∩F may

be impossible in this generality so we only approximate g.IfF is geometric and

continuous outside {p =0}, f can be approximated by a smooth function provided

that Ω is bounded (cf. Lemma 3.1.3).) As before we get (2.2.8)-(2.2.11), where we

set f

(x)=f(|x − ˆx|)=f(x) by abuse of notation. By diﬀerential inequalities in

Deﬁnition 2.1.5 at z

we get (2.2.12) if z

=ˆz,andg



) ≤ 0ifz

=ˆz. Sending

m to ∞ we obtain g



(

t)=ϕ

(

t, ˆx) ≤ 0 by using (2.1.11) and convergence results

(2.2.10), (2.2.11). This is what we wanted to prove.

(ii) It suﬃces to prove that ϕ ∈ C

2,1

(O)(resp.ϕ ∈ C

2,1

(O)) satisfy (2.1.7) (resp.

diﬀerential inequalities in Deﬁnition 2.1.5) if ϕ is a test function at ˆz of a (resp.

F-) subsolution u of (2.1.5). Let u be a subsolution in Deﬁnitions 2.1.1 and 2.1.4.

As in (i) we may assume that max in (2.1.6) is a local strict maximum and that

ϕ is a separable type : ϕ(x, t)=b(x)+g(t)withb ∈ C

)andg ∈ C

(R). We

approximate g by C

functions g

so that g

→ g locally uniformly with its ﬁrst

derivative. The rest of the proof is the same as in (i). For an F-subsolution we

may assume ∇ϕ(ˆz)=0forϕ ∈ C

2,1

(O). By (2.2.7) we may assume that ϕ is a

separable type,

ϕ(x, t)=f(|x − ˆx|)+g(t)

with f ∈F,g∈ C

(R). We do not need to approximate f; we only approximate

g by C

function. The rest of the proof is the same as in (i) so it is safely left to

the reader. 

Remark 2.2.7. From the proof of Proposition 2.2.3 we obtain the following equiv-

alent deﬁnition of an F-subsolution of (2.1.5) if F is invariant under positive mul-

tiplication. Let u : O→R ∪{−∞}fulﬁll u

∗

(z) < ∞ for all z ∈O.Thenu is an

F-subsolution of (2.1.5) in O if and only if the next two conditions are fulﬁlled.

(A) g



(

t)+F (ˆz, u

∗

(ˆz), ∇b(ˆx), ∇

b(ˆx)) ≤ 0holdsforallˆz =(ˆx,

t) ∈Oand for all

ϕ = ϕ(x, t):=b(x)+g(t)whichisC

2,1

near ˆz provided that u

∗

− ϕ attains

its local strict maximum at ˆz and that ∇b(ˆx) =0.

(B) g



(

t) ≤ 0holdsforallˆz =(ˆx,

t) ∈Oand for all

ϕ = ϕ(x, t):=f(|x − ˆx|)+g(t)

with f ∈F and with g which is C

near

t provided that u

∗

− ϕ attains its

local strict maximum at ˆz.

90 Chapter 2. Viscosity solutions

Proof of Theorem 2.2.1. We only prove the subsolution case since the case of su-

persolution follows exactly in the same way.

(i) Since

u is upper semicontinuous and u(z) < ∞ for z ∈O, our goal is to prove

(ˆz)+F (ˆz, u(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0(2.2.13)

by assuming that ϕ ∈ C

(O)andˆz ∈Ofulﬁll

max

(u − ϕ)=(u − ϕ)(ˆz).

By Proposition 2.2.2 we may assume that

u − ϕ has a strict local maximum at ˆz,

i.e.,

(

u − ϕ)(z) < (u − ϕ)(ˆz),z∈ B\{ˆz}

for some compact neighborhood of ˆz.

We set U

= u

∗

− ϕ and observe that

U = lim sup

ε→0

∗

= u − ϕ.

We now apply Lemma 2.2.5 with X = O and S = {ˆz} to get a subsequence of

} (still denoted {U

}) and a sequence {z

} in O satisﬁes

(z) ≤ U

)forz close to z

→ ˆz and U

) → U (ˆz). (2.2.14)

Since u

is a subsolution of (2.2.2) and ϕ is a test function of u

at z

, we obtain,

by Proposition 2.2.2, that

)+F

∗

), ∇ϕ(z

), ∇

ϕ(z

)) ≤ 0. (2.2.15)

Sending ε to 0 yields (2.2.13), since (2.2.1) holds and z

→ ˆz, u

∗

) → u(ˆz).

(ii) By Proposition 2.2.2 our goal is to prove diﬀerential inequalities in Deﬁnition

2.1.5 by assuming that

u − ϕ has a strict local maximum at ˆz for ϕ ∈ C

(O). By

(i) we may assume ∇ϕ(ˆz) = 0. We may take ψ in (2.2.7) instead of ϕ.

Arguing as in (i), we observe that there is a subsequence of u

(still denoted

)andz

∈Osatisfying (2.2.14). Since u

is an F

-subsolution of (2.2.2) we have

(2.2.15) if ∇ψ(z

) = 0 (i.e., z

=ˆz)andψ

) ≤ 0if∇ψ(z

)=0.Wesendε to 0

and use (2.2.4) with z

→ ˆz, u

∗

) → u(ˆz)togetϕ

(ˆz)=ψ

(ˆz) ≤ 0. 

We conclude this section by proving the equivalence of F-subsolutions and

subsolutions when (2.1.15) is fulﬁlled.

Proposition 2.2.8. Assume that (2.1.15) holds for F and that F is degenerate

elliptic. A function u : O→R ∪{−∞} is an F-subsolution of (2.1.5) (in O)if

and only if u is a subsolution of (2.1.5).

2.2. Stability results 91

Proof. Since a subsolution is always an F-subsolution under (2.1.15) it suﬃces to

prove that an F-subsolution is a subsolution. Assume that (ϕ, ˆz) ∈ C

(O) ×O

satisﬁes

max

∗

− ϕ)=(u

∗

− ϕ)(ˆz).

We may assume that u

∗

− ϕ takes its strict maximum at ˆz =(ˆx,

t)overO and

∇ϕ(ˆz)=0.Forε>0weset

(x, y, t)=u

∗

(x, t) − ψ

(x, y, t),

(x, y, t)=|x − y|

/4ε + ϕ(y,t)

and observe that

Φ(x, y, t) = (lim sup

ε→0

∗

)(x, y, t)=



∗

(x, t) − ϕ(x, t)ifx = y,

−∞ if x = y

for (x, t), (y, t) ∈O.Since

Φ takes its strict maximum at (ˆx, ˆx,

t), by convergence

of maximum points (Lemma 2.2.5 and Remark 2.2.6 (i)) a maximizer (x

)

of Φ

converges to (ˆx, ˆx,

t)asε → 0. Moreover, u

∗

) → u

∗

(ˆx,

t). Since

,y,t

) takes its maximum at y = y

,wesee

∇

)=0, ∇

ψ(x

) ≥ O,

where ∇

denotes the partial gradient in y.Since∇|x|

=4|x|

x, ∇

|x|

4|x|

+8x ⊗ x, this is equivalent to saying

−|x

− y

)/ε + ∇ϕ(y

)=0, (2.2.16)

− y

+2(x

− y

) ⊗ (x

− y

)+ε∇

ϕ(y

) ≥ O (2.2.17)

where I

denotes the N ×N unit matrix. We note that ψ

(·,y

, ·) belongs to A

an function of (x, t) (Remark 2.1.6). This is equivalent to saying that ψ

(·,y

, ·) ∈

(O) by Proposition 2.1.8.

Case A. ∇ϕ(y

) = 0 for a sequence ε = ε

→ 0.

Since (x

) is a maximum point of a function

(x, t) → u

∗

(x, t) −|x

− y

/4ε − ϕ(x − (x

− y

),t)

for ε = ε

and since u is an F-subsolution, we have

)+F (x

∗

)∇ϕ(y

), ∇

ϕ(y

)) ≤ 0

for ε = ε

. Sending ε

to zero yields

(ˆx,

t)+F

∗

(ˆx,

t, u

∗

(ˆx,

t), ∇ϕ(ˆx,

t), ∇

ϕ(ˆx,

t)) ≤ 0.

Case B. ∇ϕ(y

) = 0 for suﬃciently small ε>0.

92 Chapter 2. Viscosity solutions

This condition implies x

= y

so that ∇

)=0, ∇

O.SinceΦ

(x, y

,t) takes its maximum at (x

) as a function of (x, t), deﬁnition

of an F-subsolution (Proposition 2.1.7) yields

∂

) ≤ 0.

Sending ε to zero yields

(ˆx,

t) ≤ 0.

Since x

= y

, (2.2.16) and (2.2.17) yields

∇ϕ(y

)=0, ∇

ϕ(y

) ≥ O.

Sending ε to zero again we see

∇ϕ(ˆx,

t)=0, ∇

ϕ(ˆx,

t) ≥ O.

Since F is degenerate elliptic,

(ˆx,

t)+F

∗

(ˆx,

t, u

∗

(ˆx,

t), ∇ϕ(ˆx,

t), ∇

ϕ(ˆx,

t))

≤ 0+F

∗

(ˆx,

t, u

∗

(ˆx,

t), 0, ∇

ϕ(ˆx,

t))

≤ 0+F

∗

(ˆx,

t, u

∗

(ˆx,

t), 0,O) = 0 by (2.1.15).



2.3 Boundary value problems

So far we have discussed viscosity solutions in an open set. We seek a natural

deﬁnition of solutions for the boundary value problem. It is desirable that solutions

satisfy the stability principle. Suppose that F

∈ C

(W )convergestoF uniformly

on every compact set in W ,whereW =

Ω × [0,T] × R × R

× S

. Suppose that

∈ C

(J)convergestoB uniformly on every compact set with J = ∂Ω×[0,T]×

R × R

× S

. Suppose that u

solves

+ F

(z,u,∇u, ∇

u) ≤ 0inΩ× (0,T),

(z,u,∇u, ∇

u) ≤ 0on∂Ω × (0,T)

in a classical sense. What problem does u = lim sup

∗

ε→0

solve (when u(z) < ∞

for all z ∈

Ω × (0,T))? We consider a function ϕ ∈ C

(Ω × (0,T)) such that u − ϕ

attains a strict maximum over

Ω × (0,T)at(ˆx,

t)withˆx ∈ ∂Ω, 0 <

t<T.By

Remark 2.2.6 (i) there is a sequence z

=(x

) → (ˆx,

t) that satisﬁes

max

Ω×(0,T )

− ϕ)=(u

− ϕ)(x

Since u

solves (2.2.14), if x

∈ ∂Ω then we expect

), ∇ϕ(z

), ∇

ϕ(z

)) ≤ 0

2.3. Boundary value problems 93

under a suitable monotonicity condition of B

(Proposition 2.3.3). If x

∈ Ωthen

)+F

), ∇ϕ(z

), ∇

ϕ(z

)) ≤ 0

(under the ellipticity condition of F

). Unfortunately, for suﬃciently small ε, x

may be an interior point of Ω (Example 2.3.6), so as ε → 0 the best we expect is

either

(ˆz)+F (ˆz, u(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0

B(ˆz, u(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0.

In other words

E(ˆz, u(ˆz),ϕ

(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0

for E(z, r,τ,p,X)=(τ + F (z,r,p, X)) ∧ B(z,r,p,X). This observation shows that

the next general deﬁnition for viscosity solution is useful.

Deﬁnition 2.3.1.

(i) Let O be a locally compact subset of R

(so that every neighborhood of a

point ˆz of O includes some compact neighborhood of ˆz in O). Let E be a

lower (resp. upper) semicontinuous function on

O×R × R

× S

with values

in R ∪{−∞} (resp. R ∪{+∞}). A function u : O→R ∪{−∞} (resp.

R ∪{+∞})isa(viscosity)subsolution (resp. supersolution )of

E(z,u,Du,D

u)=0 (2.3.1)

in O if

(a) u

∗

(z) < ∞ (resp. u

∗

(z) > −∞) for all z ∈O.

(b) If (ϕ, ˆz) ∈ C

(O) ×O satisﬁes

max

∗

− ψ)=(u

∗

− ϕ)(ˆz)

(resp. min

∗

− ϕ)=(u

∗

− ϕ)(ˆz)),

(2.3.2)

then

E(ˆz,u

∗

(ˆz),Dϕ(ˆz),D

ϕ(ˆz)) ≤ 0

(resp. E(ˆz,u

∗

(ˆz),Dϕ(ˆz),D

ϕ(ˆz)) ≥ 0),

(2.3.3)

where Dϕ =(∂ϕ/∂x

)

i=1

, D

ϕ =(∂

ϕ/∂x

∂x

)

1≤i,j≤d

.HereC

(O)

denotes the set of C

functions in some neighborhood of O in R

If E is deﬁned in a dense subset of

O×R×R

×S

(with E

∗

< +∞,E

∗

> −∞

O×R×R

×S

)thenwesaythatu is a subsolution (resp. supersolution) of

(2.3.1) in O if u is a subsolution (resp. supersolution) of E

∗

(z,u,Du, D

u)=

0(resp.E

∗

(z,u,Du, D

u)=0)inO.

94 Chapter 2. Viscosity solutions

(ii) Let Ω be a domain in R

and T>0. Let F be a lower semicontinuous

function in W =

Ω × [0,T] × R × R

× S

with values in R ∪{−∞}.Let

B be lower semicontinuous in J = ∂Ω × [0,T] × R × R

× S

with values

in R ∪{−∞}.LetO be an open set in

Ω × (0,T). (For example we may

take O =

Ω × (0,T).) A function u : O→R ∪{−∞}(resp. R ∪{+∞})isa

subsolution (resp. supersolution)

+ F (z, u, ∇u, ∇

u)=0 in O∩Ω × (0,T),

B(z, u,∇u, ∇

u)=0 on O∩∂Ω × (0,T),

(2.3.4)

if u is a subsolution (resp. supersolution) of

E(z,u,u

, ∇u, ∇

u)=0 in O

in the sense of (i) with

E(z,r,τ,p, X)=



τ + F (z,r,p,X),x∈ Ω

(τ + F (z, r,p,X)) ∧ B(z,r,p, X),x∈ ∂Ωforz =(x, t)



resp.E(z,r,τ,p,X)=



τ + F (z,r,p,X),x∈ Ω

(τ + F (z, r,p,X)) ∨ B(z,r,p,X),x∈ ∂Ω.

Note that E (for subsolutions) is regarded as a lower semicontinuous function

O×R × R

× S

d−1

with d = N +1.Herea ∨ b =max(a, b).

Remark 2.3.2. By deﬁnition, u is a subsolution of (2.3.4) if and only if

(a) u

∗

(z) < ∞ for z ∈O.

(b) If (ϕ, ˆz) ∈ C

(O) ×O satisﬁes (2.1.6), then (2.1.7) holds for ˆz ∈ Ω × (0,T),

and for ˆz ∈ ∂Ω × (0,T) either

B(ˆz, u

∗

(ˆz), ∇ϕ(ˆz), ∇

ϕ(ˆz)) ≤ 0

or (2.1.7) is valid.

The similar equivalent deﬁnition is available for supersolutions.

We warn the reader that even for degenerate elliptic F , a function u ∈ C

(O)

satisfying

+ F (z,u,∇u, ∇

u) ≤ 0inO∩(Ω × (0,T)),

B(z, u,∇u, ∇

u) ≤ 0onO∩(∂Ω × (0,T))

(2.3.5)

pointwise may not be a viscosity subsolution in O unless we impose an extra

condition on B. The main reason is that the condition.

max

(u − ϕ)=(u − ϕ)(ˆx,

t)(2.3.6)

does not deduce ∇u(ˆx,

t)=∇ϕ(ˆx,

t)ifˆx ∈ ∂Ω. In fact, if ∂ΩisC

near ˆx the

condition (2.3.6) implies that either (i) or (ii) holds:

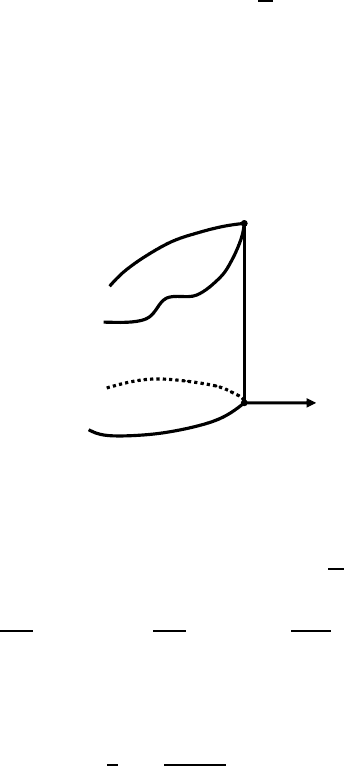
2.3. Boundary value problems 95

(i) ∇u(ˆx,

t)=∇ϕ(ˆx,

t)and∇

u(ˆx,

t) ≤∇

ϕ(ˆx,

t),

(ii) ∇u(ˆx,

t)=∇ϕ(ˆx,

t)+λνu(ˆx)and

∇

u(ˆx,

t)R

≤ R

∇

ϕ(ˆx,

t)R

− λA

for some λ>0.

Here ν(ˆx) is the outward unit normal and R

= I − ν(ˆx) ⊗ ν(ˆx);A

is the N × N

symmetric matrix whose restriction on the tangent space T

ˆx

∂Ω is the Weingarten

map of ∂Ω in the direction of ν(ˆx)andA

ν = 0. By setting v(x)=u(x,

t)− ϕ(x,

this follows from the boundary version of the classical maximum principle :

Maximum principle at the boundary. Let Ω be a domain in R

. Assume that

∂Ω is C

near ˆx ∈ ∂Ω.Letv be in C

(ˆx) ∩ Ω) with some r>0. Assume that

v(x) ≤ v(ˆx) for x ∈ B

(ˆx) ∩ Ω.

Then either

(i) ∇v(ˆx)=0and ∇

v(ˆx) ≤ O,or

(ii) ∇v(ˆx)=λν(x) and R

∇

v(ˆx)R

+ λA

≤ 0 for some λ>0.

Figure 2.5: Maximum at the boundary

Proof. We may assume v(ˆx) = 0. By translation and rotation of coordinates we

may assume that ˆx =0,ν(x)=(1, 0,...,0), R

= diag (0, 1,...,1),A

= diag

(0,λ

,...,λ

). Since v has a local maximum at 0 over Ω ∩ B

(0),

∂v

∂x

(0) = λ ≥ 0,

∂v

∂x

(0) = ... =

∂v

∂x

(0) = 0.

By expression of A

for graphs, Ω is expressed as x

<ψ(x

,...,x

)near0with

some ψ ∈ C

satisfying ∇

2

ψ(0) = A

with ∇



=(∂

,...,∂

). Since

v(x

,...,x

)=λx



j=1

∂

∂x

(0)x

+ o(|x|

)as|x|→0

96 Chapter 2. Viscosity solutions

and v takes maximum 0 over

Ω ∩ B

(0)at0,weseethatfor∇

v(0) ≤ O if λ =0

and that

λψ(x

,...,x

∇

v(0)x, x + o(|x|

) ≤ 0

for λ>0. Since ∇



ψ(0) = 0 and ψ(0) = 0, expanding ψ around zero (as a function

of x

,...,x

)nowyields

λ∇

2

ψ(0) + ∇

2

v(0) ≤ O.

This yields (ii). 

We give a suﬃcient condition for B so that a classical solution of (2.3.5) is a

viscosity solution by restricting B for the ﬁrst order operators.

Proposition 2.3.3. Let u ∈ C

(O) satisfy (2.3.5). Assume that F is degenerate

elliptic and that B depends only on (z,r,p) ∈O×R × R

. Assume that

λ → B(z,r,p − λν(x)) is nonincreasing in λ ≥ 0. (2.3.7)

Then u is a (viscosity) subsolution of (2.3.4).

Indeed, if ϕ satisﬁes (2.3.6) for ˆx ∈ ∂Ω so that (i) or (ii) holds, then by the

monotonicity assumption on B we have

B(ˆz, u(ˆz), ∇ϕ(ˆz)) ≤ B(ˆz,u(ˆz), ∇ϕ(ˆz)+λν(ˆx))

= B(ˆz,u(ˆz), ∇u(ˆz)) ≤ 0.

Remark 2.3.4. (i) Under the same monotonicity assumption on B a classical

supersolution of (2.3.4) is also a viscosity supersolution.

(ii) As in Proposition 2.2.2 we may replace the maximum by a local maximum, a

strict maximum or a local strict maximum in Deﬁnition 2.3.1 and the same remark

applies to the minimum. The proof is identical with that of Proposition 2.2.2.

(iii) As in Proposition 2.2.3 we may replace class of test functions by C

(O)or

∞

(O)fork ≥ 2 in Deﬁnition 2.3.1 (i) and even by A

(O)(k ≥ 2) or C

2,1

(O)in

Deﬁnition 2.3.1 (ii). The proof is essentially the same and it is based on Lemma

2.2.5 or Remark 2.2.6 (i).

(iv) As in Theorem 2.2.1 we have a stability result for the boundary value problem.

Since the proof is identical with that of Theorem 2.2.1 (i), we only state the results

(for subsolutions) which extends Theorem 2.2.1 (i).

(v) By deﬁnition, the localization property in §2.1.1 is still valid for (2.3.1).

Theorem 2.3.5. Let O be a locally compact subset of R

(i) Assume that E

and E are lower semicontinuous on O×R × R

× S

with

values in R ∪{−∞} for ε>0. Assume that

E ≤ lim inf

ε→0

∗

on O×R × R

× S

2.3. Boundary value problems 97

Assume that u

is a subsolution of

(z,u,Du, D

u) ≤ 0 in O.

Then

u = lim sup

∗

ε→0

is a subsolution of (2.3.1) in O provided that u(z) <

∞ for every z ∈O.

(ii) Under the notation of Deﬁnition 2.3.1 (ii) let F

and B

be lower semicontin-

uous on W and J with values in R ∪{−∞}, respectively for ε>0. Assume

that

F ≤ lim inf

ε→0

∗

in W and B ≤ lim inf

ε→0

∗

in J.

Let u

be a subsolution of

+ F

(z,u,∇u, ∇

u)=0 in O∩(Ω × (0,T)),

(z,u,∇u, ∇

u)=0 on O∩(∂Ω × (0,T)).

Then

u = lim sup

ε→0

∗

is a subsolution of (2.3.4) if u(z) < ∞ for every

z ∈O∩(

Ω × (0,T)).

The part (ii) is a trivial corollary of part (i).

Example 2.3.6. We give a simple example that a maximum point z

of u

∗

− ϕ is

not on ∂Ω× (0,T) for all suﬃciently small ε even if z

converges to ˆz ∈ ∂Ω×(0,T)

which is a maximum point of

u − ϕ where we use the notation in Theorem 2.3.5

(ii). We set

(x, t)=



∞

{g(tε, x − y)+g(tε, x + y)}u

(y)dy

with the Gauss kernel g(t, x)=(4πt)

−1/2

exp(−|x|

/4t)foru

∈ C

∞

[0, ∞)with



(0) > 0. Clearly, u

∈ C

∞

(O) is a classical solution of

− εu

=0 in Ω× (0, ∞),

=0 on ∂Ω × (0, ∞)

with Ω = (0, ∞)andO =

Ω × (0, ∞). (By Proposition 2.3.3, u

is also a viscosity

solution.) By the representation of u

the limit u = lim sup

∗

ε→0

equals u

.By

the stability results (Theorem 2.3.5) u

is a viscosity subsolution of

=0 in Ω× (0, ∞),

=0 on ∂Ω × (0, ∞).

However, evidently u

fails to fulﬁll u

(0) ≤ 0 in the strong sense by u

(0) =



(0) > 0.

We take ϕ(x, t)=u

(x)+x

+(t −

for

t>0sothatu

− ϕ takes a strict

maximum at (0,

t)=ˆz over O .Letz

be a maximum point of u

− ϕ over O.It