Ghodssi R., Lin P., MEMS Materials and Processes Handbook

Подождите немного. Документ загружается.

294 R.G. Polcawich and J.S. Pulskamp

charge (integral of the current over the speciﬁed time interval) is obtained by set-

ting the voltage to zero and solving f or the charge on the electrodes (see Equation

(5.34)). Piezoelectric materials have large but ﬁnite electrical resistivities that lead

to leakage currents. These leakage currents prevent piezoelectrics from being used

to directly sense static stress signals as the piezoelectrically generated signal typi-

cally decays rapidly. However, dynamic and resonant modes have been used to sense

static stresses.



(

)

dxdy (5.33)



dt =−



(

)

dxdy (5.34)

5.1.3.9 Equivalent Circuit Models

It is quite common for piezoelectric devices to be used at resonance. Examples

include electromechanical ﬁlters for signal processing and ubiquitous quartz crystal

microbalance that exploits the large quality factor of quartz. A common technique

of measuring the material properties of piezoelectrics involves measurement of the

frequency response of a piezoelectric resonator [20]. For such applications, the

resonator is conveniently modeled with an equivalent circuit by employing the tra-

ditional electromechanical analogy equating force with voltage and velocity with

current. A number of equivalent circuits have been developed over the years for

piezoelectric devices [31–34]. Perhaps the simplest and most commonly used is

the so-called Butterworth–Van Dyke (BVD) model (see Fig. 5.21). In the lumped

parameter one-port BVD model, the piezoelectric resonator is represented by a

series RLC circuit in parallel with a “shunt” capacitance. This shunt capacitance

represents the static capacitance of the piezoelectric material between the elec-

trodes. The RLC arm represents electromechanical equivalents of the resonator’s

mass (L

), compliance (C

), and loss (R

). These are referred to as motional terms

as they relate to the dynamic mechanical properties of the resonator. The BVD

model is valid for isolated resonances where the circuit parameters are independent

of frequency.

The electrical one-port admittance of the BVD equivalent circuit of a resonant

piezoelectric device is described by Equation (5.35) where Y

is the admittance of

the motional arm and X

is the motional reactance [35]. Equation (5.36) deﬁnes the

motional reactance in terms of t he motional inductance and motional capacitance.

At resonance, the reactance associated with the motional inductance and capacitance

cancel each other, giving the admittance as the inverse of the motional resistance

plus the admittance of the shunt capacitance. This is typically dominated by the

motional resistance term for the vibrational modes of interest.

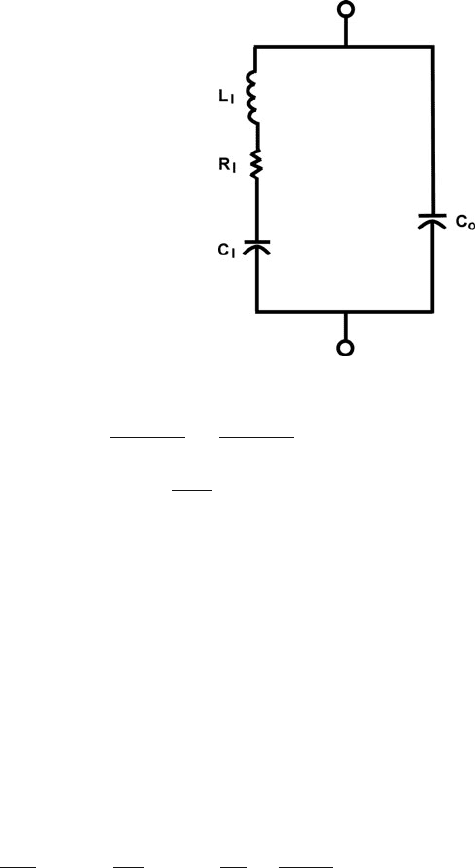
5 Additive Processes for Piezoelectric Materials 295

Fig. 5.21 BVD equivalent

circuit representation

(

)

= Y

+ jωC

+ X

− j

+ X

+ jωC

(5.35)

= ωL

−

ωC

(5.36)

The motional circuit parameter, R

, L

, and C

can be described in terms of

the relevant mechanical quantities, the resonant mode’s quality factor, and the elec-

tromechanical coupling coefﬁcient [36]. The coupling coefﬁcient η should not be

confused with the coupling factors described earlier. These terms are sometimes

used interchangeably in the literature despite their distinction. The coupling coef-

ﬁcient is analogous to the “turns ratio” of the effective transformer that converts

quantities from the electrical to the mechanical domain and vice versa. In other

words, they are the design-speciﬁc ratios of force to voltage and velocity to current.

Equation (5.37) deﬁnes the motional circuit parameters for the BVD model where

η is the electromechanical coupling coefﬁcient, Q is the mode’s quality factor, ω

the ith resonant frequency, m

ieff

is the ith effective (or modal) mass, and k

ieff

is the

ith effective spring constant.

ieff

out

ieff

Qη

(5.37)

5.1.3.10 Thin-Film Ferroelectric Nonlinearity

The constitutive equations of piezoelectricity, Equations (5.1) and ( 5.2), describe the

linear response of piezoelectric materials. These, generally, can be applied success-

fully to polar piezoelectric thin ﬁlms such as AlN and ZnO in most circumstances.

However ferroelectrics such as PZT can display pronounced stress and electric

296 R.G. Polcawich and J.S. Pulskamp

ﬁeld-induced nonlinear material responses. This is particularly true for thin ﬁlms

and actuators. Thin ﬁlms permit the application of extremely large electric ﬁelds

with modest operating voltages due to the ﬁlm thicknesses involved. Piezoelectric

MEMS actuator applications typically drive the material well beyond the coercive

ﬁeld. For a half-micron thin ﬁlm of PZT (52/48), for example, the coercive ﬁeld cor-

responds to an applied voltage of about 2.5 V. Ferroelectrics even show signiﬁcant

nonlinearity below this ﬁeld value [37]. Despite this fact it is surprising that, for

both bulk material and thin ﬁlm applications, the linear piezoelectric equations are

often used to describe the device response. To accurately model ferroelectric MEMS

device response, under high operating ﬁeld (actuators) and/or bias ﬁeld (sensors)

conditions, these signiﬁcant nonlinearities must be taken into account.

The origin of these nonlinearities in ferroelectrics is due largely to the existence

of the domain structures that are absent in the polar materials. Domain wall vibra-

tion, translation, and domain switching all contribute to the nonlinear response of

the elastic, dielectric, and piezoelectric properties. The study of nonlinearity in fer-

roelectrics is an extensive ﬁeld and a review of this topic is beyond the scope of this

book; for further information the readers are directed to [37–42].

At the high ﬁelds encountered in MEMS actuators, the total strain response is

due to the combination of the linear response, nonlinear piezoelectricity including

saturation effects, domain wall motion, and electrostriction. All dielectrics display

the property of electrostriction, whereby externally applied electric ﬁelds induce a

strain response that is proportional to the square of the ﬁeld strength. Equation ( 5.38 )

describes the total strain response in ferroelectric materials where Q is the appropri-

ate electrostrictive coefﬁcient, P

is the spontaneous polarization, E is the applied

electric ﬁeld, and κ is the appropriate dielectric constant. The ﬁrst term deﬁnes

the remnant strain. The poling process described earlier creates a macroscopically

nonzero remnant polarization. The change in this value creates a semipermanent

residual strain due to this poling process. This change in strain can be signiﬁcant

for materials such as PZT and should be accounted for in device design. The second

term is equal to the linear piezoelectric coefﬁcient (d

) multiplied by the electric

ﬁeld. The last term is the strain due to electrostriction. As the applied ﬁeld strength

increases, the electrostrictive term contributes more to the overall strain response in

the material.

x = QP

+ 2ε

κQP

E +Q

(

κE

)

(5.38)

The material responses in ferroelectrics are classiﬁed as intrinsic and extrinsic

effects. Intrinsic effects are those associated with the ionic deformations of the unit

cells of the crystalline material whereas extrinsic effects are those associated with

changes in the domain state. At large applied stresses and electric ﬁelds, signiﬁ-

cant contributions to the total strain response (Equation (5.38)) are due to nonlinear

piezoelectricity and the extrinsic response. These can be interpreted as imposing

ﬁeld and stress-dependent dielectric, elastic, and piezoelectric coefﬁcients. These

nonlinear material properties used for design purposes are best measured for spe-

ciﬁc materials and processing conditions. Due to these complex nonlinear effects,

5 Additive Processes for Piezoelectric Materials 297

Fig. 5.22 Displacement versus voltage plot for a PZT thin-ﬁlm cantilever comprised of a 0.5 μm

elastic layer (SiO

/Si

/SiO

)/0.1 μm Ti/Pt bilayer, 0.505 μm PZT (52/48), and a 0.1 μm

Pt top electrode. Key aspects of this diagram include the hysteretic displacement characteristics

upon bipolar voltage swings. In addition, all but a small fraction of the displacement occurs in one

direction

the ratio of total strain to applied electric ﬁeld is referred to as the effective electroac-

tive coefﬁcients. These coefﬁcients can be used with the models described above

using ﬁeld-dependent functions.

Perhaps the most important consequence of these nonlinear effects is the absence

of a bipolar strain response when operated above the coercive ﬁeld. Figure 5.22

shows voltage-displacement data from a simple unimorph PZT MEMS-actuated

cantilever, illustrating the so-called butterﬂy loop. The plot was obtained by sweep-

ing t he actuation voltage up to a positive voltage, then reducing to zero, then

sweeping down to a negative voltage, and ﬁnally returning to zero ﬁeld. The

extracted effective electroactive piezoelectric stress constant, e

31eff

, is illustrated in

Fig. 5.23 and corresponds to the displacement data in Fig. 5.22. This effective piezo-

electric constant includes the small signal piezoelectric effect, electrostiction, and

strain induced by large polarization charges associated with overcoming a pinched

ferroelectric hysteresis loop. An additional indication of the nonlinearity within

ferroelectric-based actuators is the nonlinearity in the dielectric constant κ

as a

function of voltage as illustrated in Fig. 5.24.

The response of the device is seen to be bipolar only in the regime between the

positive and negative coercive voltages where the negative displacement reverts to a

positive displacement (the “V” regions of the lower curves). It is instructive to con-

sider the ionic deformations of the constituent unit cells of the ferroelectric material

when considering this behavior. Referring to PZT tetragonal unit cell illustrated in

Fig. 5.6, at small values of an applied electric ﬁeld the central ion of the unit cell

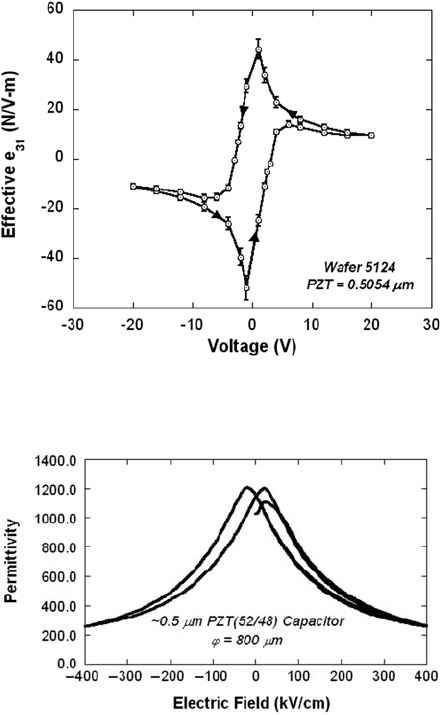
298 R.G. Polcawich and J.S. Pulskamp

Fig. 5.23 Effective electroactive piezoelectric stress constant, e

31,eff

, versus voltage extracted from

the displacement-voltage measurements for the PZT thin-ﬁlm unimorph described in Fig. 5.22

Fig. 5.24 Dielectric constant as a function of voltage for a 0.5 μm thick PZT (52/48) thin-ﬁlm

capacitor

displaces positively or negatively from its poled position, depending upon the polar-

ity of the ﬁeld. At small electric ﬁeld values, a positive displacement of the oxygen

relative to the cations creates a net elongation (c-axis) of the unit cell and a negative

displacement creates a net contraction (c-axis) of the unit cell relative to the initial

poled unit cell displacement.

However, for applied electric ﬁeld values that exceed the value necessary to

reverse the oxygen and cation sublattice displacements back to the unit cell midplane

(i.e., the coercive ﬁeld), the oxygen ions will continue to displace in the direction

of the applied ﬁeld. Once this occurs, the unit cell will no longer experience a net

contraction along the c-axis, relative to the initial poled unit cell displacement, and

instead the unit cell will experience a net elongation along the c-axis. This is due to

the mirror symmetry of the unit cell about its midplane. Thus for large electric ﬁelds

5 Additive Processes for Piezoelectric Materials 299

(i.e., in excess of the coercive ﬁeld) applied to the piezoelectric material, the s ense

of the piezoelectric strain is independent of the applied ﬁeld polarity, therefore only

a single sense of the piezoelectric strain is possible.

In terms of the device, the in-plane contraction of the piezoelectric material at

large ﬁelds gives a negative sense to the piezoelectric actuation force. The standard

conﬁguration of the d

mode MEMS unimorph, with the neutral axis below the

midplane of the piezoelectric layer gives a positive sense of the moment arm. At

small ﬁelds, with an applied voltage corresponding to the opposite of the original

poling ﬁeld (either of the lower curves in the hysteretic plot of Fig. 5.22), the actu-

ator will deﬂect downward. However, as the voltage increases to a value near the

coercive ﬁeld, the actuator will switch directions and will then bend upward. As

the ﬁeld strength is increased further, the actuator will continue to bend upward.

If instead, the polarity of the voltage corresponding to the original poling ﬁeld is

applied, the actuator will bend upward for all voltages (either of the upper curves in

the hysteretic plot of Fig. 5.22). Piezoelectric MEMS devices are most often oper-

ated under unipolar conditions and hence avoid much of the hysteresis observed in

Fig. 5.22.

5.1.3.11 Heat Generation

Piezoelectric devices are often limited in terms of drive amplitude and upper oper-

ating frequency by the generation of heat. Heat generation is due to the material

losses in the piezoelectric. Losses in piezoelectrics are mechanical, dielectric, and

electromechanical in nature. The fundamental mechanisms responsible for these

losses are complex, varied, and not fully understood. However, in ferroelectrics, the

nonmechanical losses are associated with domain and lattice affects, microstruc-

tural defects, and ﬁnite conductivity [43]. These losses have conventionally been

described by complex representations for the permittivity, compliance, and piezo-

electric material constants whereby the imaginary components refer to the losses

[44]. The heat generation is largely determined by the dielectric loss with nonres-

onant operation. The thermal power under these conditions is given by Equation

(5.39), where f is the operating frequency, Lwt

is the volume of the active

piezoelectric, and tan δ is the dielectric loss.

therm

= 2πfE

Lwt

tan δ (5.39)

5.1.4 Materials Selection Guide

The important piezoelectric and dielectric material properties for the three most

common thin-ﬁlm piezoelectrics, ZnO, AlN, and PZT are listed in Table 5.2.Afew

features to recognize are the effective thin-ﬁlm piezoelectric coefﬁcient, e

31, f

,of

these t hree compounds compared with that of PZT which is an order of magnitude

larger than the others. Furthermore, ε

33, f

is typically greater than two orders of

magnitude larger in PZT compared with ZnO and AlN.

300 R.G. Polcawich and J.S. Pulskamp

Table 5.2 Comparison of thin-ﬁlm piezoelectric materials

ZnO AlN PZT

31, f

(C/m

) –0.4 → –0.8 –0.9 → –1.1 –8 → –18

33, f

(pC/N) 10 → 17 3.4 → 6.5 90 → 150

8 → 12 10.1 → 10.7 800 → 1200

tan δ 0.02 → 0.05

Density (g/cm

) 5.68 3.26 7.5 → 7.6

Young’s Modulus (GPa) 110 → 150 260 → 380 60 → 80

Acoustic Velocity (m/s) 6.07 × 10

11.4 × 10

2.7 × 10

References [ 45–50][45, 47, 48, 51, 52][45, 47, 48]

5.1.5 Applications

Piezoelectric materials offer a combination of unique advantages in MEMS for

a wide range of applications. Generally, piezoelectric transduction utilizes strong

electromechanical coupling that features more favorable scaling and efﬁciency

than competing transduction approaches such as thermomechanical, electromag-

netic, and electrostatics. Piezoelectric sensors typically possess high sensitivity and

dynamic range and are passive devices often avoiding the need for external power.

Piezoelectric actuators are capable of low voltage/high efﬁciency operation with

large force and/or displacement generation. Although thin-ﬁlm ferroelectrics can

exhibit signiﬁcant nonlinearities, these are generally less severe than those encoun-

tered in the more prevalent electrostatic devices. The high strong electromechanical

coupling, simple geometric implementation, and high energy densities also make

piezoelectric materials attractive for energy harvesting applications.

To date, piezoelectric thin ﬁlms have been most successfully implemented in RF,

memory, and inkjet printing applications. In addition to the commercial success of

AlN ﬁlm bulk acoustic resonator (FBAR) technology [1], piezoelectric thin-ﬁlm RF

MEMS resonators [8, 48, 53–55] have now shown good insertion loss, quality fac-

tor, and motional resistances that permit straightforward integration with standard

50 RF circuits. High-performance quartz-based resonators and ﬁlters are ubiqui-

tous in RF applications, however, piezoelectric RF MEMS resonator technologies

hold the promise of much greater levels of low-cost integration by allowing multiple

lithographically deﬁned frequencies on the same chip. In recent years, piezoelectric

ﬁlms have also been utilized in high-performance RF switches, phase shifters, and

tunable capacitors [ 13, 29, 56–58]. Ferroelectric random access memory (FRAM),

a nonvolatile memory technology typically based on PZT thin ﬁlms, has been a

successful commercial product since the early 1990s. The CMOS integrated tech-

nology utilizes the ferroelectric polarization reversal with applied electric bias to

provide nonvolatile memory storage.

A wide array of sensors has been demonstrated with piezoelectric thin ﬁlms,

including acoustic microphones [59, 60], accelerometers [61–65], and ultrasound

transducers [66–69]. Recent interest in wireless sensing networks and mobile tech-

nologies has motivated great attention to energy harvesting technologies. A number

5 Additive Processes for Piezoelectric Materials 301

of groups have demonstrated low-power but high-energy-density harvesters based

on piezoelectric MEMS [70–73] using integrated proof masses and vibrational

energy-scavenging designs.

In addition to RF MEMS applications, many piezoelectric MEMS actuation tech-

nologies have been developed over the past two decades including AFM cantilever

devices [74], micromirror arrays [75, 76], inkjet printing devices [77], ultrasonic

micromotors [78, 79], mechanical logic devices [80, 81], and small-scale robotics

[16, 82–84].

5.2 Polar Materials: AlN and ZnO

This section concentrates on the purely polar compounds that have received the most

interest to date for piezoelectric MEMS: AlN and ZnO. Each of these compounds

has been researched for a wide variety of applications with ﬁlm bulk acoustic res-

onators motivating much of the research. This section reviews deposition of these

materials and patterning techniques, identiﬁes device design and processing con-

cerns, and provides examples of AlN and ZnO devices including a case study on

contour-mode resonators.

5.2.1 Material Deposition

Both AlN and ZnO are primarily deposited via physical vapor deposition tech-

niques, namely sputtering. Although metalorganic chemical vapor deposition

(MOCVD) has been used for both AlN and ZnO, most MEMS applications require

substantially thicker ﬁlms than those typically deposited by MOCVD techniques.

As a result, readers interested in information on MOCVD deposition of AlN and

ZnO are directed to [85–89]. Regardless of deposition technique, c-axis, [0001],

oriented ﬁlms, and low impurity contents are required for optimal piezoelectric

performance. Both the piezoelectric coefﬁcient and the electromechanical coupling

factor are affected by the quality of the piezoelectric crystalline texture [90, 91].

Figure 5.25 illustrates the trends in the longitudinal piezoelectric coefﬁcient, d

33,f

and the thickness mode coupling factor, k

, for sputtered AlN ﬁlms. Achieving

highly textured [0002] AlN and ZnO ﬁlms requires control of the nucleation and

growth characteristics, substrate choice, surface roughness, and defect density to

name a few parameters [91, 92]. Examples of successful deposition parameters for

both AlN and ZnO are available in Table 5.3. In general, both ZnO and AlN thin

ﬁlms are deposited via reactive sputtering using magnetron sputtering with either

RF or pulsed DC sources.

The choice of the substrate and/or the layer the piezoelectric material is to be

deposited on, can affect the properties of the piezoelectric ﬁlm greatly. For most

MEMS applications, silicon is the substrate of choice and both AlN and ZnO can be

302 R.G. Polcawich and J.S. Pulskamp

(a) (b)

Fig. 5.25 The inﬂuence of [0002] texture on (a) the longitudinal piezoelectric coefﬁcient d

33,f

factor k

Table 5.3 Sputter deposition parameters for piezoelectric AlN and ZnO thin ﬁlms

Sputtering parameter AlN AlN AlN AlN ZnO ZnO

System RF mag Triode RF mag DC pulse RF mag RF mag

Target Al Al Al Al ZnO ZnO

RF power (W) 150 200 500 80 200

Target current (A) 0.1

Target voltage (V) 1000

Target to substrate

distance (mm)

65 40 17 80

Pressure (Pa) 0.5 0.3 0.27 <0.67 2 0.93

Ar (sccm or %) 15.5 90% 3 0–10 50% 66%

(sccm or %) 2.5 10% 12 10–20

(sccm or %) 50% 33%

Bias (V or W) 0 to –100 V 0 to –250 V 0 to –320 V 0 to 12 W

Substrate

temperature (

◦

RT to 800 RT to 225 RT to 80 400 RT RT

References [101][102][103][104][105][106]

deposited onto silicon. Depending on the application, additional layers (i.e., elas-

tic layers and metal layers) may be required beneath the piezoelectric material.

One common design is to use a parallel plate conﬁguration (d

mode) in which

the piezoelectric is sandwiched between two conductive layers, as illustrated in

Fig. 5.15. The choice of the conductive layer can directly inﬂuence the crystal

texture of the piezoelectric, thereby affecting its piezoelectric properties. Common

electrode materials include Ti, Pt, and Al electrodes as they have surfaces exhibiting

hexagonal symmetry [93, 94, 104]. AlN deposited onto Pt has been shown to have

superior performance relative to Ti and Al layers (see Fig. 5.26)[104]. Recently,

there has been a push toward Mo electrodes to counter the disadvantages with Pt

including its difﬁculty in patterning, high resistivity in ultrathin layers, and higher

acoustic attenuation compared with Mo [90, 94–98]. However, Mo tends to result

in broader [0002] peaks (i.e., larger full width at half maximum, FWHM, values)

compared to Pt (see Fig. 5.27)[97, 98]. A comparison of the FWHM and surface

5 Additive Processes for Piezoelectric Materials 303

Fig. 5.26 Longitudinal

piezoelectric coefﬁcient, d

33,f

as a function of Ar/N

for

reactively sputtered AlN

deposited onto Ti, Al, or Pt

electrode layers [104]

(Reprinted with permission.

Vacuum Society)

roughness properties for sputtered AlN ﬁlms on various substrates and thin ﬁlms

is listed in Table 5.4 followed by an SEM image of AlN ﬁlm on Mo showing

the columnar growth pattern in Fig. 5.28. Methods of improving the FWHM for

AlN on Mo include the use of seed layers and buffer layers. A seed layer of Ti has

been shown to yield smoother Mo ﬁlms with a lower FWHM resulting in improved

qualities in the sputtered AlN ﬁlm (see Table 5.5)[99]. As an alternative, thin AlN

buffer layers (∼50 to 100 nm) have been used to improve the quality of AlN on Mo

ﬁlms deposited on Si substrates [100].

Similar to AlN, ZnO is primarily deposited via sputtering. A speciﬁc concern for

ZnO thin ﬁlms is the role of the oxygen partial pressure during sputtering. As shown

Fig. 5.27 Comparison

between pulse DC sputtered

AlN on Pt and Mo electrodes

[97] (Reprinted with

IEEE)