Ghodssi R., Lin P., MEMS Materials and Processes Handbook

Подождите немного. Документ загружается.

284 R.G. Polcawich and J.S. Pulskamp

Table 5.1 Deﬁnition of the electromechanical coupling coefﬁcients for elements of different

geometries

Coupling factor Resonator geometry Boundary conditions Value

nonzero



nonzero



nonzero



(thickness) x

nonzero k



(planar) x

nonzero



(



)

, nonzero



1−k



1−

(



)

(



)

that deﬁnes the strain energy density in Equation ( 5.13). However, under resonant

conditions, the strain ﬁeld is deﬁned by the relevant vibrational modeshape and is

therefore nonuniform. Thus deﬁning the ratio of stored and input mechanical and

electrical energies requires information regarding the vibrational mode in addition

to the elastic, dielectric, and piezoelectric constants. A common deﬁnition of the

effective coupling factor is given by Equation (5.14). This deﬁnes the effective cou-

pling factor in terms of the resonance (f

) and antiresonance (f

) frequencies obtained

from a one-port measurement of the admittance of a piezoelectric resonator.

eff

− f

(5.14)

5.1.3.3 Inﬂuence of Boundary Conditions

As stated earlier, the electromechanical coupling inherent to piezoelectricity leads

to a dependence of the permittivity and elastic constants on both the electrical and

mechanical boundary conditions. For example, in the case of the direct effect, a

constant external stress is applied to an equal potential electroded piezoelectric as

depicted in Fig. 5.13. The external stress generates piezoelectrically induced charges

5 Additive Processes for Piezoelectric Materials 285

Fig. 5.13 Actuation response

under different electrical

boundary conditions

on the two electrodes. Under short-circuited electrodes, current is allowed to ﬂow

between the electrodes to maintain the equal potentials. Under open-circuit condi-

tions, the charges are constrained to the electrodes and induce an internal electric

ﬁeld within the piezoelectric material. This ﬁeld, via the indirect piezoelectric effect,

actuates the material by providing stresses opposed to the externally applied stress.

The material therefore requires a greater external stress for a given deformation

under the open circuit condition and hence appears stiffer. Generally, only a lim-

ited number of the elastic constants will be inﬂuenced by the piezoelectric effect.

These modiﬁed terms are referred to as piezoelectrically stiffened elastic constants.

The permittivity has a similar response under varied mechanical boundary con-

ditions. The ratio between the mechanically clamped and free permittivities and

the electrically short- and open-circuited elastic constants are related to the elec-

tromechanical coupling factor as deﬁned by Equations (5.15) and (5.16). In the

case of high coupling factor thin-ﬁlm materials like PZT, these values can differ

signiﬁcantly.

= 1 − k

(5.15)

= 1 − k

(5.16)

5.1.3.4 Device Conﬁgurations

There exist a wide variety of piezoelectric devices and designs for bulk mate-

rial applications. A small subset of these has been implemented in MEMS device

design. Generally, MEMS devices utilize one of two operating modes, deﬁned by

the primary piezoelectric coefﬁcients employed. The “d

” mode devices feature

interdigitated (IDT) coplanar electrodes that place much of the electric ﬁeld in the

plane and are typically constructed with the active piezoelectric ﬁlm on a dielectric

286 R.G. Polcawich and J.S. Pulskamp

Fig. 5.14 Implementation of

and d

modes of

operation

layer (see Fig. 5.14). The “d

” mode devices are more common and feature parallel

plate electrodes that place the electric ﬁeld through the ﬁlm thickness (3-axis). This

mode exploits the in-plane strain resulting from the d

piezoelectric coefﬁcient.

In many bulk actuator designs, such as the multilayer stack actuator, the piezo-

electric stress/strain can be used directly. However, given the small strains, device

sizes, and process-induced variances involved, piezoelectric MEMS devices almost

exclusively utilize s ome form of displacement ampliﬁcation. The two most common

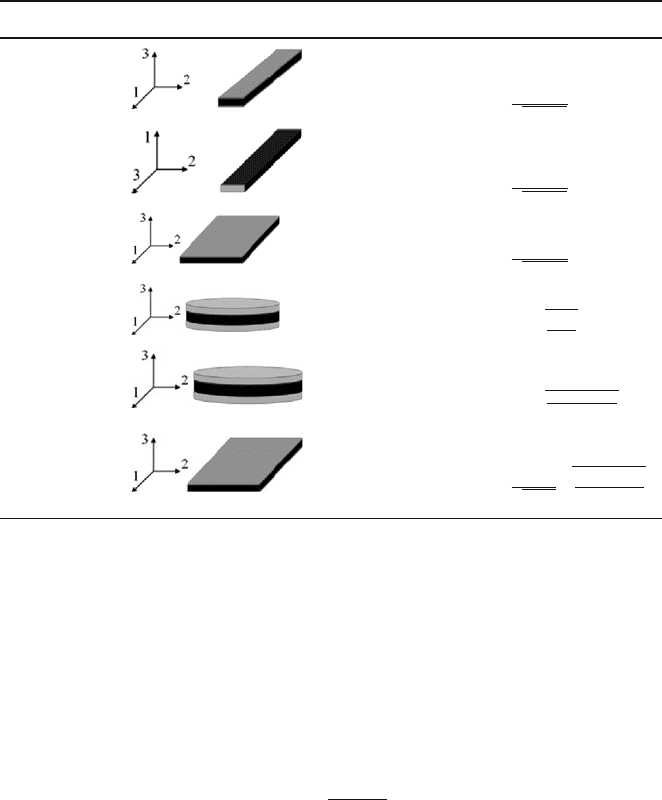
generic actuator and sensor structures are the unimorph and bimorph, both employ-

ing a form of displacement ampliﬁcation. The unimorph is a structure that features

an electroded piezoelectric attached to a structural or elastic layer (see Fig. 5.15).

Application of an electric ﬁeld to the piezoelectric layer leads to ﬂexure of the struc-

ture and applied stresses can also lead to a voltage developed across the electrodes.

The bimorph (see Fig. 5.15) features two active piezoelectric layers that are operated

with opposite sense strain to produce ﬂexure and similarly may be used in sensing

mode like the unimorph. Membrane structures are also quite common in piezoelec-

tric MEMS applications and differ from their electrostatic counterparts largely in

terms of the optimal electrode design to account for the induced strain nature of

operation. Similar to other MEMS transduction t echniques, ﬂexural leverage has

also been implemented to produce larger displacements in piezoelectric MEMS

actuators. This is particularly true for the recently demonstrated in-plane actuator

designs [16].

Fig. 5.15 Piezoelectric

unimorph (top) and bimorph

(bottom). Note: The bimorph

can be used without the

internal elastic layer and

instead using a common

electrode for both

piezoelectric layers

5 Additive Processes for Piezoelectric Materials 287

5.1.3.5 Free Strain and Blocking Force

Before addressing more detailed device models, it is useful to consider the max-

imum possible strain, displacement, and force that can be generated by a piezo-

electric actuator. The free strain  represents the piezoelectrically induced strain

obtained in a completely mechanically free (zero force condition) material and

hence is the maximum attainable strain for a given electric ﬁeld. Equation (5.17)

deﬁnes the free strain associated with the d

mode of operation where V is the

applied voltage and t

is the thickness of the piezoelectric layer. In contrast, the

term “free displacement” refers to the actuator displacement obtained when the

actuator moves in the absence of external forces. The free displacement is there-

fore the maximum possible nonresonant static displacement for a given actuator

design operating under a given electric ﬁeld. The actual strain, the induced strain, in

the piezoelectric layer will generally be less than the free strain due to the inﬂuence

of the nonpiezoelectric components in the actuator.



= d

(5.17)

The “blocking force” represents the piezoelectrically induced force obtained in

a completely mechanically clamped (zero strain condition) material and hence is

the maximum attainable force for a given electric ﬁeld. Equation (5.18) deﬁnes

the actuation force of an actuator associated with the d

mode of operation where

is the extensional stiffness of the piezoelectric layer, Y

is the elastic modulus

of the piezoelectric, and w is the width of the actuated section. For most MEMS

structures, the appropriate d

or e

coefﬁcient or constant is the “effective” value

discussed in Section 5.1.1. This actuation force can be interpreted as the blocking

force of the mechanically free piezoelectric layer only. Figure 5.16 illustrates the

force-displacement response for typical actuator designs, with linear stiffness prop-

erties. For a given electric ﬁeld, the force-displacement response is deﬁned by the

blocking force (zero displacement – x intercept) and the free displacement (zero

force – y intercept). Points along the force-displacement curve represent the possi-

ble conditions where the actuator performs work against an external load. Increasing

the electric ﬁeld shifts the response up and to the right. The region below the curve

deﬁned by the maximum operating ﬁeld provides the possible force-displacement

responses of that particular design. Displacement ampliﬁcation schemes allow the

Fig. 5.16 Plot of the

force/strain (displacement)

relationship for a

piezoelectric actuator

288 R.G. Polcawich and J.S. Pulskamp

designer to trade force and displacement by altering the slope of the curves illus-

trated in Fig. 5.16. This information is useful in determining whether a given

actuator design can drive a given external load.

act

(

)



= d

31, f

wV (5.18)

5.1.3.6 Cantilever Unimorph Model

There is extensive treatment of modeling piezoelectric sensors and actuators avail-

able in the literature with varying degrees of accuracy and ease of implementation

in design [17–26]. What follows is a model that approximates piezoelectric actua-

tor response that agrees well with ﬁnite element analysis and is easily implemented

for design purposes. The complexity of the differential equations describing the

exact piezoelectric response limits the analytical modeling of these devices to the

simplest cases. Although ﬁnite element modeling i s typically employed for more

complex device design, analytical models can still provide valuable design insights.

As stated earlier, the unimorph is a structure that features an electroded piezoelectric

attached to a structural layer. A simple unimorph actuator bends due to the piezo-

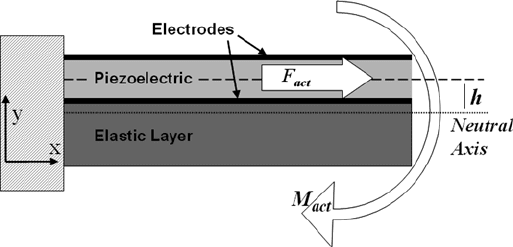
electrically induced bending moment acting about its neutral axis (see Fig. 5.17).

The actuation force, Equation (5.18), is the resultant of the piezoelectric stresses

and acts near the midplane of the piezoelectric layer. The mechanical asymmetry

of the structure about the piezoelectric layer, due to the presence of the structural

layer, leads to the generation of the actuation moment. In the case of a cantilevered

actuator (see Fig. 5.17) the sense of the strain within the piezoelectric layer and the

relative position of the line of action of the actuation force with respect to the struc-

ture’s neutral axis determine the direction of motion. Equation (5.19) deﬁnes the

piezoelectric actuation moment where h is the distance between the line of action of

the actuation force and the relevant neutral axis of the composite actuator.

act

= F

act

h = d

31, f

wVh (5.19)

Fig. 5.17 Schematic representative of a thin ﬁlm piezoelectric unimorph cantilever

5 Additive Processes for Piezoelectric Materials 289

Equation (5.20) deﬁnes h in terms of the location of the actuation force, y

Fact

and the neutral axis referenced to the same arbitrary axis. For most structures, the

actuation force is assumed to act at the midplane of the piezoelectric layer.

h = y

Fact

−¯y (5.20)

A convenient method for treating composite structures in ﬂexure is the trans-

formed section method [27]. This method converts the various dissimilar material

layers of the composite to a common material with a transformed cross-section. The

layers of the new cross-section have altered widths to maintain the same stiffness

properties as the previous sections with the beam now of a homogeneous material.

This cross-section is mechanically equivalent, in ﬂexure, to the original compos-

ite beam but may be treated with conventional analysis. The method permits the

determination of the location of the neutral axis, bending stresses, and ﬂexural stiff-

ness properties of the composite structure. An arbitrary material in the composite

is chosen as the homogeneous material of the transformed cross-section. The cross-

sectional areas of the new layers of a composite comprised of individually isotropic

elastic materials are given by Equation (5.21) where w

and t

are the original width

and thickness, respectively, of the ith layer, Y

is the modulus of elasticity, and Y

ref

is the modulus of the reference layer.

= w

ref

(5.21)

The location of the bending neutral axis is given by Equation (5.22) where y

the distance from each layer’s centroid to some arbitrary reference axis and A

tot

the total area of the transformed section.

¯y =



tot

(5.22)

In the case of the cantilevered actuator, the equivalent loading of the piezoelec-

tric is that of moment applied at the end of the electroded beam. The linear free

displacement of the cantilevered unimorph actuator is described, from Bernoulli–

Euler beam theory, by Equation (5.23) where L is the length of the electrode, M

act

is the bending moment acting on the actuator, and YI

is the ﬂexural rigidity of the

composite actuator.

tip

act

2YI

31, f

wVhL

2YI

(5.23)

For many designs, the cantilevered piezoelectric actuator is capable of extremely

large displacements. The dominant mechanical nonlinearity in these cases is due

to the geometric (small displacement) nonlinearity. Again, for the case of the

290 R.G. Polcawich and J.S. Pulskamp

cantilevered piezoelectric actuator with a constant end applied moment, this non-

linearity is easily described [28]. Equations (5.24) and (5.25) describe the vertical

and horizontal free displacements, respectively.

tip

act



1 − cos



act



(5.24)

tip

= L −



act



sin



act



(5.25)

The ﬂexural rigidity of the composite YI

describes the bending stiffness of the

actuator and is the product of the modulus of elasticity and the moment of inertia

(second moment of area) of the beam with respect to the neutral axis. Employing the

transformed section method and the parallel axis theorem, Equation (5.26) deﬁnes

where I

is the moment of inertia of the ith layer about its own centroid and d

the distance between the ith layer’s centroid and the neutral axis [27].

= Y

ref







+ A



(5.26)

Some problems, such as modal analysis, often require an equivalent modulus

of elasticity of the composite structure. In the preceding discussion, use of the

transformed section method deﬁned the section properties in terms of an arbi-

trary homogeneous material. An equivalent modulus of elasticity Y

is deﬁned

by Equation (5.27) which applies to structures where the separate layers behave

mechanically in parallel.





tot



(5.27)

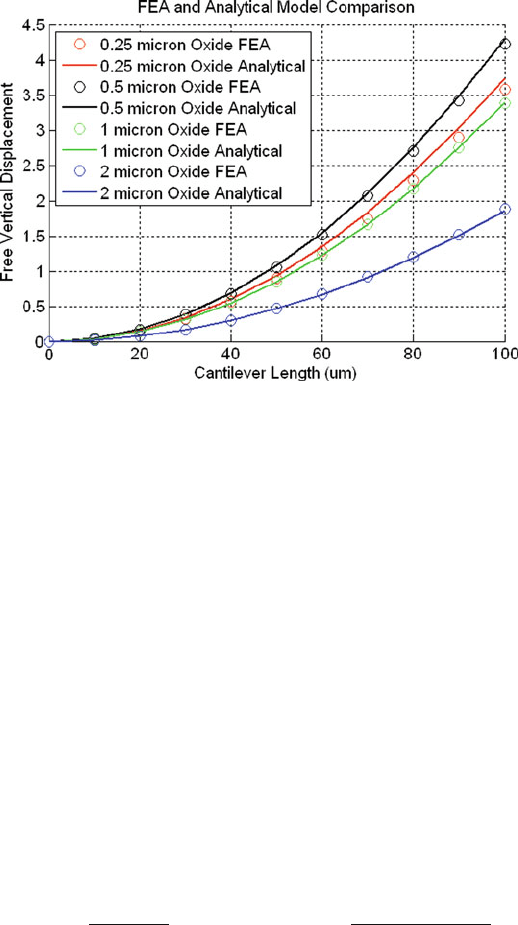
The method just described agrees well with ﬁnite element analysis. Figure 5.18

compares the results of a commercially available FEA package and the analytical

model above for a d

mode unimorph cantilever with a PZT active layer operating

at 5 V for various ratios of piezoelectric to structural layer. The unimorph (or struc-

ture) is a silicon dioxide/platinum/PZT/platinum prismatic beam. The FEA model

utilized 3-D ten-node tetrahedral structural and directly coupled ﬁeld solid elements.

The analytical model generally agrees within 1–3% of the ﬁnite element analysis.

As discussed previously in Section 5.1.1, the ﬁlm clamping effects in the major-

ity of piezoelectric MEMS structures result in effective d

31, f

coefﬁcients and e

31, f

constants. The 1-D analytical model described above utilizes these values directly

as these terms directly relate, for example, d

31, f

, the 1-axis strain response in the

structure to the electric ﬁeld applied along the 3-axis. However, in a 2- or 3-D FEA

analysis that accommodates the full piezoelectric coefﬁcient matrix, the actual coef-

ﬁcients should be speciﬁed using Equation (5.12). The method can also easily be

modiﬁed to describe the response of bimorph devices.

5 Additive Processes for Piezoelectric Materials 291

Fig. 5.18 Comparison of FEA and analytical modeling of piezoelectric unimorphs

5.1.3.7 Actuator Force Generation Against External Loads

The force exerted by a piezoelectric actuator depends upon the particular conﬁgu-

ration used. Two general cases of interest are of a cantilever exerting a purely axial

force against an external load and that of a unimorph or bimorph acting against a

normal load. A symmetric composite actuator that is capable of extensional dis-

placements only can be used to drive a MEMS ﬂexure. In this case, the force

produced by the actuator is related to the actuation force of the actuator and the

ratio of the stiffnesses of the actuator and ﬂexure. Equation (5.28) relates the force

exerted by the actuator on a MEMS ﬂexure where k

ext

is the spring constant of the

ﬂexure and L

act

is the dimension of the actuator along the axis of displacement.

The equation illustrates the importance of the actuator stiffness when designing an

actuator for driving a speciﬁc load. When the actuator is very much stiffer than the

ﬂexure, the actuator is unconstrained, the force exerted by the actuator is zero, and

no work has been done on the load (F = 0). At the other extreme, when the ﬂex-

ure is much stiffer than the actuator, the actuator is completely clamped, the force

exerted by the actuator is equal to the blocked force, and again no work has been

done (x = 0).

F = F

act



1 −

act

− k

ext



= d

31, f



1 −



− L

act

ext



(5.28)

Similar behavior is observed for a unimorph or bimorph acting against a normal

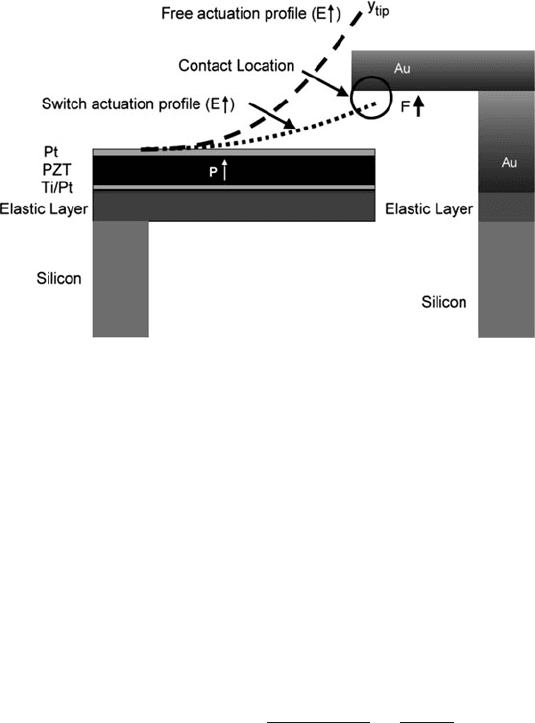
load. This scenario is encountered in most piezoelectric RF MEMS switch designs

where a unimorph or bimorph actuator closes a pair of electrical contacts through

vertical displacements. The PZT RF MEMS switch design of Polcawich et al. [29]

292 R.G. Polcawich and J.S. Pulskamp

Fig. 5.19 Schematic diagram of contact loading for a piezoelectric switch actuator

features a pair of unimorph actuators mechanically coupled at their free ends to a

structure containing the switch contacts. Voltage applied to the actuators vertically

displaces the contacts up into a set of contact cantilevers. Figure 5.19 illustrates a

simple model of this structure depicting a partially electroded cantilever unimorph

with a normal contact force at the switch contact location (this assumes the contact

cantilever is rigid; i.e., inﬁnite k

ext

)[30]. In this case, the f orce exerted by the actua-

tors can be approximated by the product of the actuator stiffness and the difference

between the initial gap and the free displacement. Equation (5.29) relates the force

exerted by the actuator on the contact beam for the simple case where the force is

exerted at the location of the end of the electrode and g

is the initial gap between

the actuator and the contact.

F = k

act



tip

− g



31, f

wVh

act

−

act

(5.29)

5.1.3.8 Piezoelectric Sensing

The preceding discussion described basic models for the behavior of piezoelec-

tric actuators by use of the converse or indirect effect (Equations (5.6) and (5.8)).

Piezoelectric materials may also be utilized for sensing and power harvesting

applications. The constitutive equation for the direct effect, Equations (5.7) and

(5.9), describe the dependence of the electric displacement on external stresses.

Piezoelectric sensors generally measure this response either through the voltage

developed on open-circuited electrodes or by the current (or charge via integration)

through short-circuited electrodes with the aid of additional signal-conditioning

electronics. Equation (5.30) describes the charge developed on the electrodes in

terms of the electric displacement where the integration is carried out over the entire

electrode area of the piezoelectric.

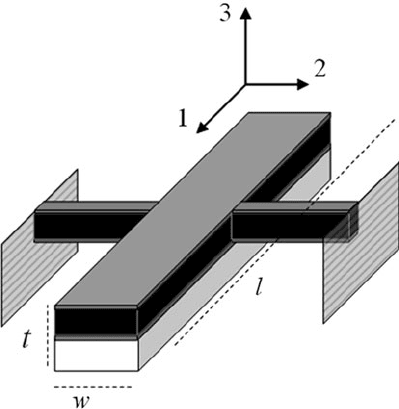
5 Additive Processes for Piezoelectric Materials 293

Fig. 5.20 Resonant free–free

beam device

q =



]

⎡

⎣

⎤

⎦

(5.30)

Consider a large aspect ratio piezoelectric structure vibrating in a length exten-

sional mode (see Fig. 5.20). Equation (5.31) describes the charge developed on the

electrodes of such a structure where the only nonzero stress is along the 1-axis that

is normal to the plane of the beam structure. Carrying out the integration on the sec-

ond term on the right-hand side and substituting the deﬁnition from electrostatics of

voltage in terms of electric ﬁeld (note the negative sign), we obtain Equation (5.32).

The ﬁrst term is the charge due to the static capacitance of the piezoelectric sensor

and the second is the piezoelectrically induced charge due to the external stress. This

expression describes the essence of piezoelectric sensor operation.

q =−

⎛

⎝



(

)

dxdy +



dxdy

⎞

⎠

(5.31)

q = C

V −



(

)

dxdy (5.32)

The open circuit voltage is obtained by setting the charge to zero and solving

for the voltage across the electrodes (see Equation (5.33)). The short-circuit total