Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

191
125,0
3
4
2
2
34
5,0
1
=
⋅
⋅
⋅
⋅
⋅=
y
D
.
Как видно, в данном случае дисперсия выходной переменной в че-
тыре раза меньше дисперсии входного воздействия типа белого шума.
Когда к рассматриваемой системе приложено воздействие
)(
2
tϕ
,
спектральная плотность её выходной переменной имеет вид
2
2
2
4
2
24)(3
2
)(
22
ω++ω+ω
=ω
jj
S
yy
.
Подставив это произведение в формулу (4.74), получим
=
∫
ω
ω++ω+ω
π
=
∞
∞−
d
jj
D
y
2
2
2
4
2
24)(3
2
2
1
2
=ω
∫
ω+
+ω+ω
π
=
∞
∞−
d
j
jj
2
2
2
2
2
24)(3
2
2
1
ω
∫
+ω+ω+ω
π
=
∞
∞−
d
jjj
2
23
410)(10)(3
22
2
1
.
В этом случае дисперсия вычисляется по формуле Мак-Лена для
3
=
n
. При этом
22
0
=b
,
0
21
== bb
,
4
0
=c
,
10
1
=c
,
10
2
=c
,
3
3
=
c
. В результате получим
1136,0
2
=
y
D
.
Таким образом, рассматриваемая система подавляет цветной шум
)(
2
tϕ
примерно в 1,1 раза лучше, чем белый шум
)(
1
tϕ
.
Формирующий фильтр. Из выражения (4.75) видно, что при дейст-
вии белого шума на входе линейного звена с передаточной функцией
constpW
≠
)(
выходная переменная представляет собой реализацию
некоторого случайного коррелированного процесса, т.е. цветного шума.
Поэтому можно считать, что всякий цветной шум есть результат прохож-
дения белого шума через некоторое динамическое звено, которое и при-
дает цветному шуму его специфические свойства: коррелированность и
неравномерную спектральную функцию. Такие звенья принято называть
формирующими фильтрами.
Чтобы упростить процесс исследования динамических систем при
случайных воздействиях влияние коррелированных воздействий стре-
мятся заменить влиянием эквивалентных белых шумов. Для этой цели

192
используются формирующие фильтры. Поэтому возникает задача по-
строения математической модели формирующего фильтра для заданного
коррелированного воздействия.
Определение передаточной функции формирующего фильтра для
случайного воздействия с заданной спектральной плотностью достаточно
очевидно из формулы (4.47).
Действительно, спектральная плотность
)(ω
ϕϕ
S
всегда является
чётной функцией частоты
ω
. Поэтому её можно представить в виде
(4.11), т.е. в виде квадрата модуля отношения двух полиномов мнимого
аргумента
ω
j
. С другой стороны, если на вход динамического звена с
передаточной функцией
)(
)(
)(
pc
pb
pW =
(4.76)
подать белый шум со спектральной плотностью
1)( =ω
ϕϕ
S
, то в соот-
ветствии с выражением (4.47) выходная переменная этого звена будет
представлять собой реализацию некоторого случайного процесса со
спектральной плотностью
2
)(
)(
)(
ω
ω
=ω
jc
jb
S
yy
. (4.77)
Следовательно, можно заключить, что звено с передаточной функ-
цией (4.76) является фор мир ующи м фи ль тро м для случайного про-
цесса со спектральной плотностью (4.77).
Отметим, что в общем случае звено с передаточной функцией (4.76)
может быть как физически реализуемым, так и физически не реализуе-
мым, т.е. иметь
n
m
≤
или
n
m
≥
, где
)(deg pbm
=
, а
)(deg pcn
=
.
Применение формирующих фильтров позволяет, как отмечалось
выше, при исследованиях динамических систем, находящихся под влия-
нием случайных воздействий, заменить влияние реальных коррелирован-
ных случайных воздействий влиянием белых шумов. Эта замена осуще-
ствляется путём включения в число уравнений модели системы уравне-
ний соответствующих формирующих фильтров.
Уравнения системы совместно с уравнениями формирующих
фильтров случайных воздействий образуют модель, так называемой,
расширенной системы [8, 9].
193
Г л а в а 5
ДИСКРЕТНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
§ 5.1. Дискретные переменные и их модели
Наряду с обычными непрерывными системами, движения которых
описываются непрерывными функциями времени, на практике широко
применяются импульсные или дискретные системы. Информация о со-
стоянии таких систем представляется импульсными или дискретными
переменными.
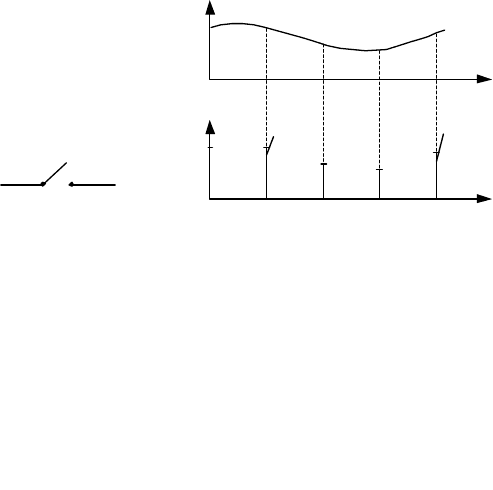
Дискретная переменная получается из непрерывной, в результате
подачи её на вход импульсного элемента, который формирует очень ко-
роткие по длительности импульсы. Такой элемент обычно изображают в
виде ключа, который схематически показан на рис. 5.1,а. Замыкаясь на
очень короткое время, ключ формирует с периодом Т функцию
)(tg
∗
,
которая представляет собой последовательность
δ
-импульсов, опреде-
ленных в моменты времени
kTt
k
=
,
,...2,1,0
=
k
. Площадь каждого из
этих импульсов равна значению переменной
)(tg
в соответствующие
моменты времени, как показано на рис. 5.1,б.
T
g (t)
g* (t)
g
g*
δ
g(T) (t-T)
δ
4g(T)
(t-4T)
0
T
2T 3T
4T t
0
t
a)
б)
Рис. 5.1
Определение решетчатой функции. Математически работу ключа
можно описать выражением
∑
∞
=
∗
−δ=
0
)()()(
k
kTtkTgtg
. (5.1)

194
В выражении (5.1)
)(t
δ
– это дельта-функция (см. параграф 2.5).
Преобразование (5.1) называется к ва нт ов ани ем п о вр ем ени не-
прерывной функции
)(tg
. Результат квантования по времени, т.е. функ-
ция
)(tg
∗
называется р еш етч ат ой ф унк цие й. Решетчатые функции,
таким образом, описывают импульсные или дискретные воздействия и
переменные дискретных динамических систем. Другими словами, решет-
чатые функции являются моделями дискретных воздействий и перемен-
ных дискретных динамических систем.
Решетчатые функции (5.1) часто обозначают как функции дискрет-
ного аргумента
,...2,1,0
=
k
, т.е. вместо
)(tg
∗
пишут:
)(kTg
,
][kg
или
k
g
, причем
)(][ kTggkg
k
==
.
Для решетчатых функций вводятся понятия конечных разностей и
сумм, которые в некотором смысле соответствуют понятиям производ-
ной и интеграла для непрерывных функций [7].
Конечные разности. Выражение
]1[][][
−
−
=
∆
kgkgkg
(5.2)
называется нисходящей к онеч но й р азност ью пе рво го п оря дка
решетчатой функции
][kg
.
Выражение
][]1[][ kgkgkg −+=∆
(5.3)
называется восходящей конечной разностью первого порядка.
Обычно величины
][kg
∆
и
][kg∆
для краткости часто называют
просто п ер вые ра зно сти.
Так как в технических устройствах, работающих с реальными пере-
менными, определить при
kTt
=
фигурирующие в (5.3) будущие значения
]1[
+
kg
невозможно, то в дальнейшем рассматриваются лишь нисходя-
щие первые разности, первая из которых определяется выражением (5.2).
Первая разность от решетчатой функции
][kg
∆
, т.е. функция
]1[][][
2
−∆−∆=∆ kgkgkg
, (5.4)
называется конечной разностью второго порядка или просто в тор ой
ра зно сть ю.

195
Аналогично определяются разности более высоких порядков. На-
пример, п-я разность – это решетчатая функция
]1[][][
11
−∆−∆=∆
−−
kgkgkg
nnn
. (5.5)
Важной особенностью разностей является то, что любую из них
можно выразить через значения соответствующей решетчатой функции.
Например, подставляя (5.2) в (5.4), получим
]2[]1[2][][
2
−+−−=∆ kgkgkgkg
.
Аналогично
]3[]2[3]1[3][][
3
−−−+−−=∆ kgkgkgkgkg
.
Для п-й разности справедлива формула [7]
( )
][1][
0
1
ν+−
ν
−=∆
∑
=ν
+ν
nkg
n
kg
n
n
. (5.6)
Здесь
!)(!
!
ννν
ν
−
==
n
n
C
n
n
. (5.7)
Соотношения (5.5) и (5.6) позволяют выразить и саму решетчатую
функцию через ее разности. Например,
∑
ν∆
ν
=
=ν
ν
n
g
n
ng
0
][][
. 5.8)
Формула (5.8) является дискретным аналогом разложения непре-
рывных функций в ряд Тейлора.
Запаздывающие и опережающие решетчатые функции. Отме-
тим, что
]1[
−
kg
можно рассматривать как некоторую решетчатую
функцию, за па зд ыва ющ ую на Т (говорят: на такт или на период) по
отношению к
][kg
. Тогда функция
][][ mkgkf
−
=
является запазды-
вающей на т периодов по отношению к
][kg
. Аналогично, разностная
функция
][][ mkgkf +=
является о пер еж ающ ей на т периодов раз-
ностной функцией.

196
Суммирование решетчатых функций. Эта операция является об-
ратной по отношению к операции взятия первой разности.
Пусть дана решетчатая функция
][kg
,
,...2,1,0
=
k
. Необходимо
найти такую решетчатую функцию
][kG
, первая разность которой
равна
][kg
. Очевидно
∑
+ν=
=ν
k
GgkG
0
1
]0[][][
, (5.9)
где
]0[
1
G
– некоторая постоянная, причем
]0[]0[]0[
1
gGG −=
.
Действительно, согласно (5.9)
∑
−
=ν
+ν=−
1
0
1
]0[][]1[
k
GgkG
. Поэтому
по определению первой разности находим
∑ ∑
=−=∆
=
−
=
k k
kgggkG
0
1
0
][][][][
ν ν
νν
.
По аналогии с определенным интегралом функцию
][kG
называют
оп ред еле нной су ммо й для функции
][kg
.
Z-преобразование. При исследовании дискретных систем широко
используется дискретное преобразование Лапласа или z-преобразование.
Z-п реоб ра зо ва нием функции
)(tg
∗
или
)(tg
вещественного пе-
ременного
t
называется функция комплексного переменного
z
, опреде-
ляемая [6, 7] формулой
∑
=
∞
=
−
0
][)(
k
k
zkTgzg
. (5.10)
Символически это преобразование записывается в виде
)}({)( tgZzg
=
.
Существует связь между z-преобразованием и непрерывным преоб-
разованием Лапласа. Эта связь устанавливается соотношением
pT
ez
tgZtgL
=
∗∗
= )}({)}({
,
где
)(tg
∗
определяется формулой (5.1).

197
Преобразование Лапласа и z-преобразование часто встречающихся
функций приведены в приложении П.7.
Укажем основные свойства z-преобразования.
- теорема линейности
)(][
11
∑∑
=ν
νν
=ν
νν
=
NN
zgсkgcZ
; (5.11)
- теорема упреждения
∑
−=+
−
=
−
1
0
][)(]}[{
m
i
im
zigzgzmkgZ
; (5.12)
- теорема запаздывания
)(]}[{ zgzmkgZ
m−
=−
; (5.13)
- теоремы о предельных значениях
)()1(lim][lim][
1
zgzkgg
zk
−==∞
→∞→
,
)(lim][lim]0[
0
zgkgg
zk ∞→→
==
. (5.14)
Здесь
][ig
,
][ ig
−
,
mi ,...,1,0
=
– начальные значения решетчатой
функции. Кроме того, в (5.14) предполагается, что изображение первой
разности решетчатой функции
][kg
является аналитической функцией
на окружности единичного радиуса, а также вне её на комплексной плос-
кости z [7].
Другие свойства z-преобразования приведены в [6, 7].
Формула обращения. Как и в случае непрерывного преобразования
Лапласа, решетчатая функция-оригинал z-преобразования определяется
по ее z-изображению формулой обращения, т.е.
∫
π
==
−−
C
k
dzzzg
j
zgZkg
11
)(
2
1
)}({][
, (5.15)
где
1−
Z
– символ обратного z-преобразования; интегрирование в (5.15) про-
водится по окружности
C
радиуса
C
e
(причем
C
C
σ>
) в положительном
направлении;
C
σ
– абсцисса абсолютной сходимости функции
)(
zg
.
198
Для вычисления оригинала применяется также теорема о вычетах,
по которой
ν
ν
zz
l
k
zzgkg
=
=
−
∑
=
1
1
)( Res][
, (5.16)
где
ν
z
– полюс функции
1
)(
−k
zzg
, лежащий внутри окружности
C
в
(5.15);
l
– число полюсов функции
)(zg
.
Если полюс
ν
z
простой, то
}))(({lim)( Res
11 −
ν
→
=
−
−=
ν
ν
k
zz
zz
k
zzzzgzzg
. (5.17)
Если полюс
ν
z
имеет кратность
ν
r
, то
}))(({lim
)!(
1
)( Res
1
1
1
1
1 −
−
ν
−
−
→
ν
=
−
ν
ν
ν
ν
ν
−
ν−
=
k
r
r
r
zz
zz
k
zzzzg
dz
d
r
zzg
.
Одним из самых простых способов обращения является разложение
z-изображения на простейшие дроби и применение таблиц, содержащих
z-изображения простейших функций (см. П.7). Этот способ будет рас-
смотрен ниже на примерах.
§ 5.2. Уравнения дискретных систем
Функциональную схему большинства импульсных систем можно
представить, как показано на рис. 5.2, где обозначено ИЭ – импульсный
элемент, НЧ – непрерывная часть системы.
y
ε
g
ИЭ
Н Ч
u
и
Рис. 5.2
Чаще всего импульсный элемент периодически (с периодом Т)
формирует прямоугольные импульсы длительностью
и
τ
. Амплитуда
импульсов пропорциональна значениям входного сигнала
)(t
ε
импульс-
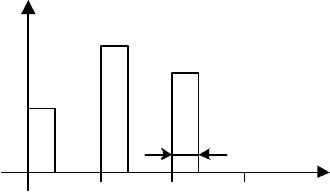
199
ного элемента в дискретные моменты времени
kTt
=
,
K,2,1
=
k
Гра-
фик выходной переменной
и
u
ИЭ для этого случая приведен на рис. 5.3.
τ
kT
2TT
u
и
u
и
(0)
u
и
(Т)
u
и
(2Т)
и
0
Рис. 5.3
Зависимость, представленная на рис. 5.3, описывается следующими
выражениями
+≤≤τ+
τ+≤≤ε
=
TktkT
kTtkTkTk
tu
)1(,0
],[
)(
и
ии
и
. (5.18)
Здесь
и
k
– коэффициент передачи ИЭ.
Непрерывные части (НЧ) импульсных систем (рис. 5.2) являются
обычными непрерывными системами, которые рассматривались в преды-
дущих главах. Поэтому уравнения НЧ в переменных состояния анало-
гичны, скажем уравнениям (1.8), (1.9), и имеют вид
инн
ubxAx
+=
&
, (5.19)
xcy
Т
н
=
. (5.20)
Уравнения импульсных систем являются разностными, так как
обычно описывают соотношения только между дискретными значениями
входного воздействия
)(
kTg
, рассогласования
)(
kT
ε
, выходного сигна-
ла
)(
kTy
и дискретными значениями переменных состояния
][
kTx
не-
прерывной части. Для вывода этих уравнений можно применить формулу
Коши (2.132).
Применяя эту формулу к уравнению (5.19), получим

200
ττ+=
∫
τ−
−
dubexetx
t
t
tA
ttA
)()(
ин
)(
0
)(
0
н0н
. (5.21)
Положим в (5.21)
kTt =
0
,
Tkt ]1[
+
=
,
][
0
kTxx =
и проведём за-
мену переменных. В результате будем иметь
∫
+
τ−+−+
=ττ+=+
Tk
kT
TkTAkTTkTA
dubekTxeTkx
)1(
ин
)()(
)(][])1[(
нн
=
=+=τ
==τ
=τ
+=τ
=
TvTk
vkT
dvd
kTv
,)1(
0,
dvvkTubekTxe
vTA
T
TA
)(][
ин
)(
0
нн
++=
−
∫
.
В соответствии с рис. 5.3 и выражением (5.18) величина
)(
и
ν+kTu
на интервале от
и
τ+kT
до
TkT
+
равна нулю, а в интервале от
kT
до
и
τ+kT
равна
][
и
kTk ε
. Поэтому из предыдущего выражения следует
∫
τ
−
ε+=+
и
нн
0
ин
)(
.][][])1[( dvkTkbekTxeTkx
vTATA
(5.22)
Равенства (5.20) и (5.22) можно записать следующим образом
][][]1[ kbkxAkx ε+=+
, (5.23)
][][ kxcky
T
=
. (5.24)
Здесь обозначено
ин
0
)(
и
нн
, kdvbebeA
vTATA
∫
τ
−
==
,
н
сс
=
. (5.25)
