Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.


161
).()225,2()()23()()7( pyppgppup
+
−
−
+
=
+
(3.103)
С тем, чтобы упростить схему регулятора, введём в уравнение
(3.103) отклонение
y
g
−
=
ε
, заменив сигнал
g
в соответствии с выра-
жением
.
y
g
+
ε
=
В результате уравнение регулятора примет вид
)(25,5)()23()()7( ppypppup
+
ε
+
=
+
. (3.104)
Реализация регулятора. Для построения структурной схемы регу-
лятора найдём сначала его уравнения в переменных состояния. С этой
целью запишем уравнение (3.104) в векторно-матричной форме
),()()( ppWpu
uv
ν=
где
T
pypp ])()([)( ε=ν
– вектор входов регулятора, а
++
+
=
7
25,5
7
23
)(
p
p
p
p
pW
uv
(3.105)
передаточная матрица регулятора.
Выделим сначала целые части скалярных передаточных функций в
(3.105) в соответствии с приведённым выше алгоритмом перехода от пе-
редаточных матриц к уравнениям в переменных состояния (см. § 3.2).
Далее, применяя при
1
=
n
соотношения (3.48), (3.49) (так как у регуля-
тора два входа и один выход), получим
,75,36197 yxx
−
ε
−
−
=
&
(3.106)
.25,53 yxu
+
ε
+
=
(3.107)
Нетрудно проверить, что замкнутая система, состоящая из объекта
(3.102) и регулятора (3.106), (3.107), имеет заданную передаточную функ-
цию (3.101).
162
Г л а в а 4
ДИНАМИЧЕСКИЕ СИСТЕМЫ ПРИ СЛУЧАЙНЫХ
ВОЗДЕЙСТВИЯХ
§ 4.1. Случайные воздействия и процессы
Динамические системы наряду с регулярными воздействиями, кото-
рые описываются детерминированными функциями времени, испытыва-
ют влияние и слу чай ны х воздействий. Такими воздействиями называют
силы, которые не могут быть описаны детерминированными функциями.
Случайные воздействия не повторяются при повторных наблюдениях, и
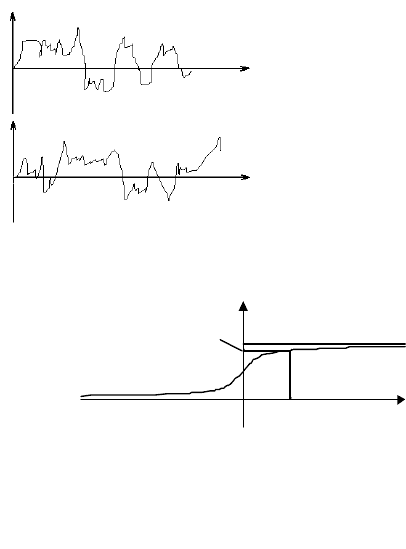
значения их непредсказуемы. Результаты двух наблюдений
)(
1
tϕ
и
)(
2
tϕ
за случайным воздействием
)(t
ϕ
приведены на рис. 4.1. Говорят,
что
)(
1
tϕ
,
)(
2
tϕ
– различные р еа лиза ци и одного и того же случайного
воздействия.
Для описания случайны х воздействий в математике введено понятие
случайного процесса. По форме случайные процессы совпадают со случай-
ными воздействиями. С луч айный
пр оце сс – это функция времени, зна-
чения которой распределены в соответ-
ствии с некоторым законом распреде-
ления. График одного из таких законов
приведен на рис. 4.2. Здесь по оси абс-
цисс отложены значения, которые мо-
жет принимать случайный процесс, т. е.
числа от
∞
−
до
∞
+
, а по оси ординат
вероятность того, что процесс
)(t
ϕ
будет иметь значение, меньшее величи-
ны
i
x
, в каждый момент времени существования процесса
)(t
ϕ
.
Случайные процессы различаются по виду закона распределения. В тео-
рии динамических систем чаще всего рассматриваются случайные процессы
t
t
1
ϕ
2
ϕ
0
0
Рис. 4.1
1
x
P
ϕ
( x
i
)
0
x
i
P
Рис. 4.2

163
процессы с нормальным (гауссовским) законом распределения [7, 14].
Если параметры закона распределения не меняются со временем, то
соответствующий случайный процесс называется ста ци она рным, ина-
че – не ста цио на рны м.
Параметрами закона распределения являются так называемые ста -
тист ич еские хар ак тер ист ики , к которым относятся:
• математическое ожидание (среднее значение);
• дисперсия;
• корреляционная функция;
• спектральная плотность.
Эти характеристики называются статистическими потому, что они
определяются как средние значения некоторых случайных функций от
)(t
ϕ
, т.е. в результате усреднения этих функций.
Усреднение при определении статистических характеристик может
проводиться как по множеству реализаций, так и по времени. В частно-
сти, величина
∑
ϕ=ϕ
=
∞→
n
i
i
n
t
n
tM
1
)(
1
lim))((
(4.1)
называется сред ним по мно жеств у, а величина
∫
ττϕ=ϕ
+
−
∞→
Tt
Tt
T
d
T
t )(
2
1
lim)(
(4.2)
называется сред ним по вр ем ени .
В зависимости от соотношения значений среднего по множеству и
среднего по времени случайные процессы делятся на эргодические и не-
эргодические. Если статистические характеристики процесса, определён-
ные путём усреднения по времени, совпадают с характеристиками, полу-
ченными в результате усреднения по множеству, то процесс называется
эр го ди чески м.
В дальнейшем будем рассматривать в основном случайные эргоди-
ческие процессы. Это предположение делается с целью упрощения мето-
дики исследования, так как оно позволяет определять все статистические
характеристики путем усреднения по времени, что практически значи-
тельно проще, чем усреднение по множеству.
В зависимости от величины среднего значения
)(t
ϕ
процессы де-
лятся на:
• цен тр ир ова нны е, если
0)(
=
ϕ
t
;
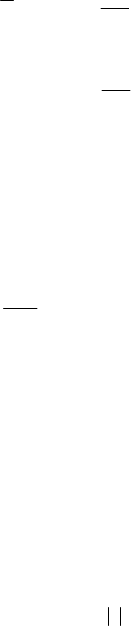
164
• не ц ен три ро ва нны е, если
0)(
≠
ϕ
t
.
Переход от не центрированного случайного процесса к центриро-
ванному осуществляется путем вычитания из значений не центрирован-
ного процесса его среднего значения, поэтому в дальнейшем будем счи-
тать рассматриваемые процессы центрированными. Тогда
0)(
2
1
lim)( ≡ττϕ=ϕ
∫
+
−
∞→
Tt
Tt
T
d
T
t
, (4.3)
constd
T
tD
Tt
Tt
T
=ττϕ=
∫
+
−
∞→
ϕ
)(
2
1
lim)(
2
. (4.4)
Выражение (4.4) определяет дисп ер сию случайного стационарно-
го процесса
)(t
ϕ
, которая является его энергетической характеристикой
и численно равна его мощности.
Величина
∫∫
∞
∞−−
∞→
ϕϕ
τ+ϕϕ=τ+ϕϕ=τ dtttdttt
T
R
T
T
T
)()()()(
2
1
lim)(
(4.5)
называется ко рре ля цио нно й (ав ток орр еля цион но й) фу нкци ей
центрированного случайного стационарного процесса
)(t
ϕ
. Она описы-
вает связь между значениями этого процесса, отстоящими друг от друга
на величину
τ
.
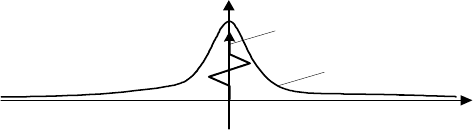
В зависимости от значения этой функции различают процессы
типа:
• бе ло го шум а (при
)()( τδ=τ
ϕϕϕ
DR
);
• ц вет но го ш ум а (при
)()( τδ≠τ
ϕϕϕ
DR
,
например, при
τα−
ϕϕϕ
=τ eDR )(
).
Графики корреляционных функций указанных случайных процессов
приведены на рис. 4.3.
165
Функцию, определяемую формулой (4.5), можно определить по от-
ношению к двум различным случайным процессам
)(t
ϕ
и
)(t
ψ
следую-
щим образом
.)((t))(
∫
ττ+ψϕ=τ
∞
∞−
ϕψ
dtR
(4.6)
Функция
)(τ
ϕψ
R
называется вза имно й к орр еляц ио нно й ф унк -
ци ей двух случайных процессов
)(t
ϕ
и
)(tψ
.
Если процессы
)(t
ϕ
и
)(tψ
не зависят друг от друга, то
0)( ≡τ
ϕψ
R
тождественно, иначе
0)( ≠τ
ϕψ
R
.
Спе ктра ль ная пло тно сть случайного процесса
)(t
ϕ
определя-
ется выражением
∫
∞
∞−
ωτ−
ϕϕϕϕ
ττ=ω deRS
j
)()(
(4.7)
и фактически является преобразованием Фурье от корреляционной функ-
ции этого процесса. Интеграл в (4.7) всегда вещественная функция, так
как
)(τ
ϕϕ
R
– чётная функция.
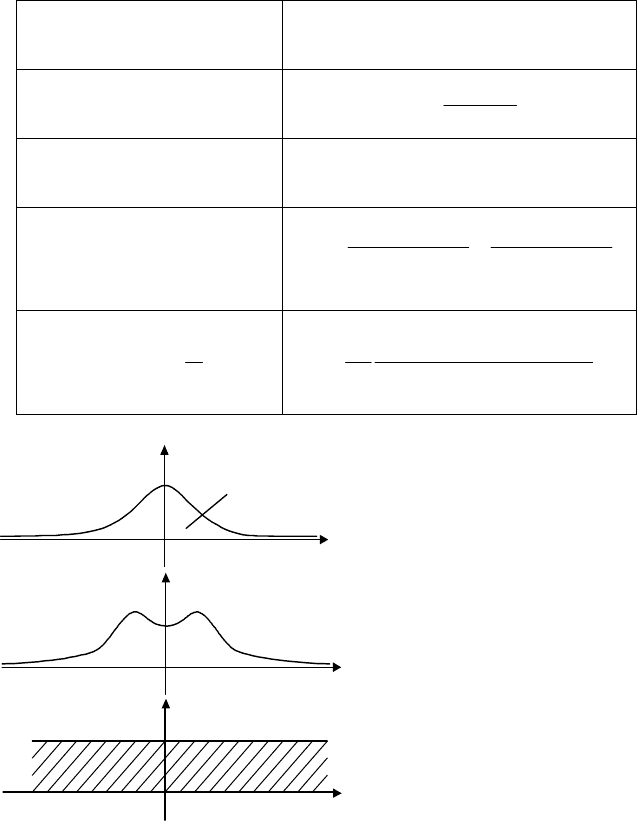
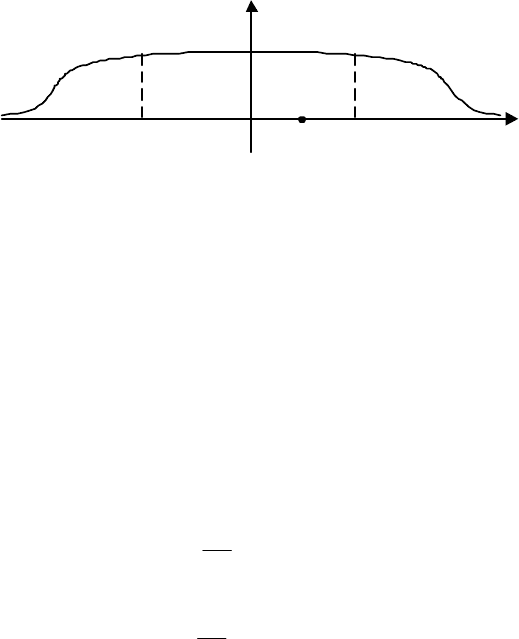
Спектральная плотность характеризует распределение мощности
сигнала по его спектральным составляющим. Графики наиболее часто
используемых зависимостей
)(ω
ϕϕ
S
приведены на рис. 4.4, а выражения
для корреляционных функций
)(τ
ϕϕ
R
и соответствующих спектральных
плотностей
)(ω
ϕϕ
S
приведены в таблице 4.1.
белого шума
цветного шума
0
τ
R
Рис. 4.3
166
Таблица 4.1
)(
τ
ϕϕ
R
)(
ω
ϕϕ
S
||τα−
ϕ
eD
22
2
ω+α
α
ϕ
D
)(τδ
ϕ
D
ϕ
D
βτ
τα−
ϕ
cos
||
eD
ω+β+α
+
ω−β+α
α
ϕ
2222
)(
1
)(
1
D
βτ
β
α
+βτ
τα−
ϕ
sincos
||
eD
222222
22
4)(
4
ωβ−ω+β+α
β+α
π
ϕ
a
D
Мощность белого шума,
как площадь под прямой
)(
ω
ϕϕ
S
(см. рис. 4.4,в),
равна бесконечности. Это
означает, что белый шум
есть идеализация. Вводится
этот случайный процесс с
целью упрощения расчётов.
Фактически, белый шум ис-
пользуется как пробное воз-
действие, аналогичное иде-
альной ступенчатой функции
или дельта-функции, кото-
рые тоже являются идеали-
зацией некоторых реальных
воздействий.
Модель – случайный
процесс типа белого шума
используется в тех случаях, когда спектральная плотность реального слу-
чайного воздействия имеет вид, приведенный на рис. 4.5. Другими сло-
а)
б)
в)
мощность сигнала
S
ϕϕ
(ω)
ω
0
S
ϕϕ
(ω)
0
S
ϕϕ
(ω)
0
ω
ω
Рис. 4.4
167
вами, тогда, когда в некоторой полосе частот
),(
maxmax
ωω−
спектраль-
ная плотность
)(ω
ϕϕ
S
реального воздействия практически постоянна.
Например, в том случае, когда в выражении
|)|exp()( τα−=τ
ϕϕϕ
DR
вели-
чина
α
очень большое число, а рабочая полоса частот
),0(
r
ω
исследуемой
системы уже полосы
max
,0 ω
, т.е. если
max
ω<ω
r
, как показано на рис. 4.5.
Вза им на я спе ктра ль на я п ло тн ость это также преобразова-
ние Фурье, но от взаимной корреляционной функции, т.е.
∫
∞
ωτ−
ϕψϕψ
ττ=ω
0
)()( deRjS
j
. (4.8)
Эта функция характеризует распределение мощности взаимодейст-
вия двух случайных процессов по частоте
ω
и в общем случае является
комплексной функцией.
В практических задачах часто необходимо находить корреляци-
онную функцию по спектральной плотности. Для этой цели используется
обратное преобразование Фурье, т.е.
,)(
2
1
)(
∫
ωω
π
=τ
∞
∞−
ωτ
ϕϕϕϕ
deSR
j
(4.9)
или
.)(
2
1
)(
∫
∞
∞−
ωτ
ϕψϕψ
ωω
π
=τ dejSR
j
Полагая в (4.9)
τ
равным нулю, получим формулу для определения
дисперсии случайного процесса
ω
ω
max
−
ω
max
ω
r
0
ϕϕ
S
Рис. 4.5
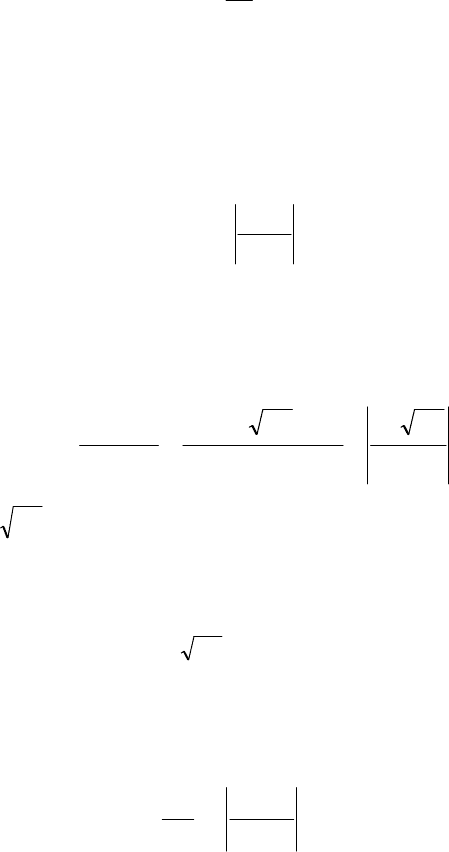
168
∫
∞
∞−
ϕϕϕϕϕ
ωω
π
== dSRD )(
2
1
)0(
. (4.10)
Как видно из приведённых выше формул (см. таблицу 4.1), спек-
тральная плотность чаще всего является отношением полиномов, содер-
жащих только чётные степени частоты
ω
. Это позволяет спектральную
плотность
)(ω
ϕϕ
S
представить в виде квадрата модуля отношения поли-
номов от переменной
ω
j
, т.е.
2
)(
)(
)(
ω
ω
=ω
ϕϕ
jc
jb
S
, (4.11)
где
)(
ω
jb
,
)(
ω
jc
– некоторые полиномы от
ω
j
.
Пример 4.1. Приведем к виду (4.11), например, выражение для
)(ω
ϕϕ
S
из второй строки приведенной выше таблицы 4.1. Имеем
2
2
22
2
))((
|2|2
)(
ω+α
ασ
=
ω−αω+α
ασ
=
ω+α
α
=ω
ϕϕϕ
ϕϕ
jjj
D
S
,
где
ϕϕ
=σ D
– среднеквадратическое отклонение случайного процесса
)(t
ϕ
от среднего значения.
Соотнося полученное выражение с (4.11), заключаем, что в данном
случае
)(2 ω=ασ
ϕ
jb
,
)(
ω
=
ω
+
α
jcj
.
Подставляя выражение
)(ω
ϕϕ
S
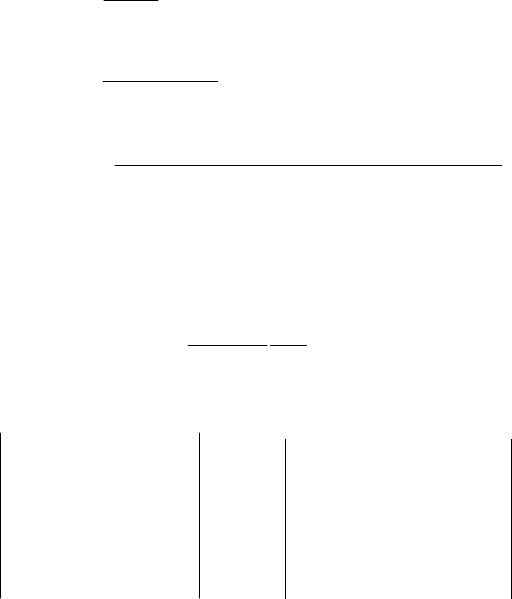
из (4.11) в формулу (4.10), получим
∫
∞
∞−
ϕ
ω
ω
ω
π
= d
jc
jb
D
2
)(
)(
2
1
, (4.12)
где в общем случае:
169
1
110
)()()(
−
−
ω++ω+=ω
n
n
jbjbbjb K
,
n
n
jcjccjc )()()(
10
ω++ω+=ω K
.
Правая часть в формуле (4.12) обычно обозначается
n
I
(в зависимо-
сти от степени полинома
)(
ω
jc
) и вычисляется в общем виде, т.е. когда
коэффициенты
)(
ω
jb
и
)(
ω
jc
обозначены символами. Результаты обыч-
но представляются в зависимости от степени знаменателя и приводятся в
литературе. Называются они формулами Мак-Лена.
Приведем эти формулы для некоторых значений n:
1
=
n
10
2
0
1
2 cc
b
I =
,
2
=
n
210
2
2
00
2
1
2
2 ccc
cbcb
I
+
=
,
3
=
n
)(2
)2(
213030
32
2
03020
2
110
2
2
3
cccccc
ccbccbbbccb
I
+−
+−+
=
.
При более высоких значениях n или при вычислении дисперсии по
(4.12) на ЭВМ представляется более целесообразным использование сле-
дующей формулы [7]:
n
n
n
n
n
Г
N
c
I
2
)1(
1+
−
=
где
02
1
01
2
31
00
0
00
00
сс
с
сс
сс
сс
Г
n
nn
nn
n
K
KMM
O
MMK
K
−
−
−−
=
,
02
1
01
2
0121
00
0
00
сс
с
сс
с
c
gggg
N
n
nn
nn
n
K
KMM
O
MMK
K
−
−
−−
=
.
170
Здесь
i
g
– коэффициенты полинома
0
42
2
22
1
)()()()()( gjgjgjbjbjg
n
n
n
n
++ω+ω=ω−ω=ω
−
−
−
−
K
.
Фактически
n
Г
это определитель Гурвица, составленный для по-
линома
01
1
1
)( cscscscsc
n
n
n
n
++++=
−
−
K
, а
n
N
это тот же оп-
ределитель, в котором коэффициенты первой строки заменены коэффи-
циентами
i
g
полинома
)(
ω
jg
при
i
j
2
)( ω
.
Формулы Мак-Лена позволяют вычислить дисперсию
ϕ
D
случай-
ного процесса
)(t
ϕ
по формуле (4.12), если известна его спектральная
плотность
)(ω
ϕϕ
S
. Однако они справедливы, если только все корни
полинома
)(sc
имеют отрицательные вещественные части.
В процессе распространения случайных процессов в динамической
системе они могут складываться и вычитаться, поэтому приведем форму-
лы статистических характеристик суммы и разности случайных процес-
сов.
Обозначим
)()()( tytxtz
±
=
и предположим, что заданы:
)(τ
xx
R
,
)(τ
yy
R
,
)(ω
xx
S
,
)(ω
yy
S
и
)( ω
jS
xy
,
)( ω
jS
yx
.
Тогда имеют место формулы [9]:
)()()()()( τ±τ±τ+τ=τ
yxxyyyxxzz
RRRRR
, (4.13)
+
ω
=
ω
±
ω
+
ω
=
ω
)()(Re2)()()(
xxxyyyxxzz
SjSSSS
)()()(
ω
±
ω
±
ω
+
jSjSS
yxxyyy
. (4.14)
Отметим также, что в общем случае можно записать:
)(Re)(Re ω=ω
jSjS
yxxy
,
)(Im)(Im
ω
−
=
ω
jSjS
yxxy
. (4.15)
Подчеркнем, что приведенные выше формулы используются при
определении статистических характеристик выходных сигналов дина-
мических систем.
