Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

141
Заменяя последовательные соединения элементов и соединения с
обратной связью эквивалентными блоками
61012
WWW =
,
8613
WWW =
,
12514
WWW −=
,
141115
WWW =
,
137
7
16
1 WW
W
W
+
=
,
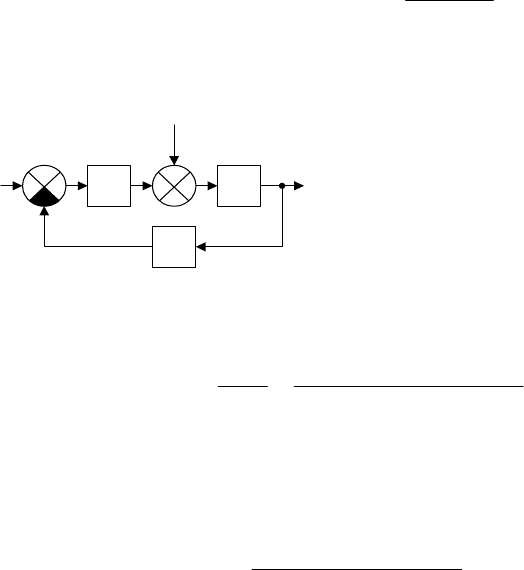
получим схему, состоящую всего лишь из трех элементов, которая при-
дена на рис. 3.14.
Полученная простая струк-
турная схема исследуемой системы
дает возможность непосредственно
записать передаточные функции,
например,
)(pW
yg
и
)(pW
yf
на
основе принципа суперпозиции.
Так, исключая воздействие
f
,
получаем соединение в виде от-
рицательной обратной связи. По-
этому по формуле (3.70) найдем
)()()(1
)()(
)(
)(
)(
16158
1615
pWpWpW
pWpW
pg
py
pW
yg
+
==
.
Аналогично, исключив из схемы воздействие
g
, тоже получим со-
единение, в котором звено
16
W
охвачено отрицательной обратной связью
с
158
WWW
ос
=
. Поэтому снова по формуле (3.70) получим
)()()(1
)(
)(
16158
16
pWpWpW
pW
pW
yf
+
=
.
Определение передаточных функций по формуле Мейсона. Как
видно из приведенных выше примеров, конечная цель преобразований
структурных схем заключается в получении настолько простой схемы
системы, чтобы непосредственно по ней можно было бы записать пере-
даточные функции системы между некоторыми входами и некоторыми
выходами. Ясно также, что если схема сложная, то метод последователь-
ных преобразований требует очень больших затрат времени и труда для
определения необходимых передаточных функций.
W
15
W
16
W
8
g y
f
Рис. 3.14
142
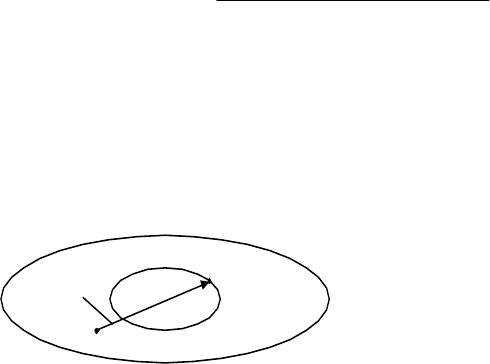
Формула Мейсона (Mason’s gain formula) удобна тем, что позволяет
найти передаточную функцию между любыми двумя точками сколь угодно
сложной структурной схемы, как показано на рис. 3.15 (на этом рисунке
структурная схема условно показана двумя эллипсами). При этом схема не
подвергается никаким преобразованиям.
Формула Мейсона имеет вид
∗
=
∗
=
=
∏
−
∏
−
∑
=
q
j
kj
q
j
kj
k
i
пi
ab
pW
pWpW
pW
1
*
1
1
))(1(
))(1()(
)(
, (3.73)
где
)(pW
пi
– передаточная функция i-го пр ям ого п ути из a в b;
k
–
число прямых путей из точки а в точку b;
)(pW
kj
– передаточная функ-
ция j-го за мк ну то го к он тур а;
q
– общее число замкнутых контуров
всей структурной схемы.
Передаточные функции
прямых путей и контуров со-
ставляются с учетом знаков
суммирующих элементов. Знак
*
{}
– означает, что из суммы,
стоящей в фигурной скобке в
(3.73), необходимо исключить
слагаемые, содержащие произ-
ведение самой на себя хотя бы
одной передаточной функции.
Замечание. Перед применением формулы Мейсона в структурной
схеме необходимо обозначить различным образом передаточные функ-
ции всех ветвей. В частности тех ветвей, в которых отсутствуют элемен-
ты и передаточная функция которых формально равна единице. При этом
под ве твью с хем ы понимается участок, фрагмент или связь между
двумя узлами, двумя точками суммирования (вычитания) или между уз-
лом и точкой суммирования (вычитания).
Рассмотрим порядок применения формулы Мейсона (3.73) на при-
мере конкретной структурной схемы.
W
ab
(p)
a
b
Рис. 3.15
143
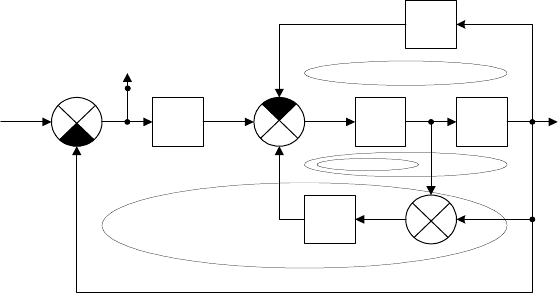
Пример 3.9. Для системы, структурная схема которой приведена на
рис. 3.16, найти передаточные функции между точками a и b, а также
между точками a и c.
Решение. Прежде всего, обозначим цифрой
µ
1
,
5,4,3,2,1
=
µ
пе-
редаточные функции ветвей, не имеющих элементов. Эти обозначения
показаны на рис. 3.16 и достаточно очевидны. При этом порядок нумера-
ции значения не имеет.
Для определения искомых передаточных функций найдем сначала
знаменатель. В данной схеме число замкнутых контуров
4
=
q
. Их пере-
даточные функции
2451235423211
1111 WWWWW
k
−=−=
,
232352
1WW
k
=
,
1253
1WW
k
=
,
2344
WW
k
−=
.
I
IIIII
IV
W
4
W
2
W
3
W
1
W
5
1
3
1
2
1
5
1
1
1
4
a
g
c
b
ε
y
Рис. 3.16
По формуле (3.73) находим знаменатель искомой передаточной
функции
)(pW
ab
×−−+=
−=
∏
=
)11)(11)(11{())(1(
12523235245123
*
1
WWWpWA
q
j
kj
=−++−=+×
∗ *
12523424512323235234
)}11)(111{()}1( WWWWW
24512323235125234
1111 WWWW +−−+=
.

144
Перейдем к определению числителя передаточной функции
)(pW
ab
. В данном случае из a в b имеется лишь один прямой путь, т.е.
1
=
k
. Передаточная функция этого пути
51231
1WW
п
=
.
Поэтому по формуле (3.73) числитель будет иметь вид
=
∑
∏
−=
∗
=
=
k
i
q
j
kjпi
pWpWB
1
*
1
))(1()(
}
{
.)1111(1
123
*
245123232351252345123
WWWWWW =+−−+=
Передаточная функция
5
1
в конечном результате опущена. Следо-
вательно, передаточная функция между точками
a
и
b
12323525234
123
1)(
)(
)(
WWWW
W
pg
py
pW
yg
+−−+
==
.
Перейдем к определению
)(pW
ac
. Согласно (3.73) знаменатель
)(pW
ac
совпадает со знаменателем
)(pW
ab
. Поэтому сразу ищем чис-
литель
)(pW
ac
. Здесь также
1
=
k
, причем
51
1=
п
W
. Поэтому в данном
случае
{
}
23525234
*
245123232351252345
1)1111(1 WWWWWWWB −−+=+−−+=
.
Следовательно, искомая передаточная функция
12323525234
23525234
1
1
)(
WWWW
WWW
pW
g
+−−+
−
−
+
=
ε
.
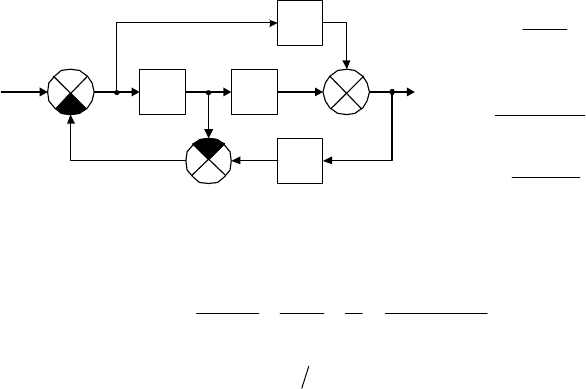
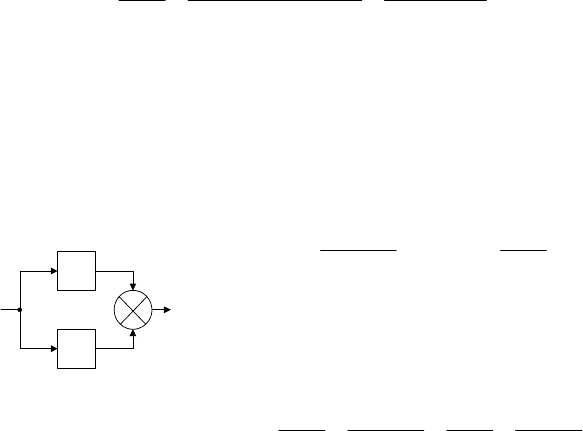
Пример 3.10. Найти передаточную функцию
)(pW
ab
для системы,
показанной на рис. 3.17, где
1
2
)(
1
+
=
p
pW
,
4)(
2
=pW
,
p
pW
1
)(
3
=
,
2)(
4
=pW
.
Решение. Как и в предыдущем случае, сначала обозначим
µ
1
пере-
145
даточные функции ветвей без элементов, а затем найдем знаменатель. В
данном случае число замкнутых контуров системы
3
=
q
. Их передаточ-
ные функции имеют вид
1431231
1WW
k
−=
,
23412
1WW
k
=
,
143343
1WW
k
−=
.
Находим знаменатель. По формуле (3.73) он равен
{
}
=+−+=
*
143342341143123
)11)(11)(11( WWWA
{
}
=+−+=
*
143342341143123
)11)(111( WWW
.1111
143342431143123
WWW +−+=
Находим числитель. В данном случае
2
=
k
, причем
13121
1WW
п
=
,
1342
1WW
п
=
.
Следовательно, числитель
{
}
412
*
1343423411341231341312
)1111)(11( WWWWWWWB +=+−++=
.
Подставляя численные значения, найдем, что числитель равен
=+
+
⋅= 2
1
2
4
p
B
=
+
++
=
1
228
p
p
1
102
+
+
=
p
p
.
Аналогично найдем,
что знаменатель определяется выражением
)1(
102
1
28
1
2
2
+
++
=+
+
−
+
+=
pp
pp
pp
pp
A
.
Поэтому, беря отношения
AB
, найдем передаточную функцию
рассматриваемой системы
W
1
W
2
W
4
W
3
a
g
y
b1
3
1
4
1
2
1
1
Рис. 3.17
146
10
102
)10)(1(
)1()102(
)(
)(
)(
2
2
2
++
+
=
+++
++
==
pp
pp
ppp
ppp
pg
py
pW
yg
.
§ 3.5. Преобразование структурных схем по уравнениям
в переменных состояния
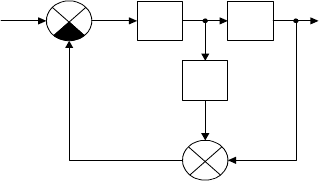
Рассмотрим сначала динамическую систему, схема которой приве-
дена на рис. 3.18. Передаточные функции элементов определяются сле-
дующими выражениями
)1(
1
)(
1
+
=
pp
pW
,
1
3
)(
2
+
=
p
pW
.
Передаточная функция рассматриваемой
системы по правилу определения передаточ-
ной функции для случая параллельного со-
единения звеньев имеет вид
pp
p
ppppg
py
pW
+
+
=
+
+
+
==
2
13
1
3
)1(
1
)(
)(
)(
.
Рассматривая это равенство как пропорцию, получим
)()31()()(
2
pgppypp +=+
.
Далее, переходя в этом выражении к оригиналам, найдем дифферен-
циальное уравнение вход–выход системы, приведенной на рис. 3.18,
)(3)()()( tgtgtyty
&&&&
+
=
+
.
В соответствии с полученным уравнением данная схема является
системой второго порядка (т.к. старшая производная выходной величины
равна двум). В тоже время из структурной схемы и передаточных функ-
ций элементов видно, что первый элемент имеет 2-й порядок, а второй
элемент – 1-й порядок. Следовательно, на самом деле порядок системы
равен трем. Это означает, что в процессе преобразования моделей вход-
выход произошла, как и в случаях, описанных выше, потеря информации
о структуре системы. Сохранилась лишь информация о связях выхода с
входом. Подчеркнем еще раз, что эта особенность, связанная с возмож-
ной потерей информации о некоторых свойствах динамических систем,
характерна для преобразования любых моделей вход-выход.
W
1
W
2
g y
Рис. 3.18
147
Для того чтобы исключить подобные недоразумения, необходимо
использовать более корректное преобразование моделей систем. Одним
из таких преобразований является преобразование моделей в переменных
состояния, которое не приводит к потере информации о состоянии сис-
темы в целом [3].
Для проведения этого преобразования структурной схемы каждый
её элемент должен быть задан своими уравнениями в переменных со-
стояния. Эти уравнения могут быть получены, например, аналитическим
методом, рассмотренным в первой главе. Для простых элементов (перво-
го, второго порядка) они могут быть получены из передаточных функ-
ций, как уравнения минимальной реализации, одним из рассмотренных
выше методов перехода от моделей вход-выход к моделям в переменных
состояния. Эта возможность в случае простых элементов (звеньев) объ-
ясняется тем, что простые динамические звенья, как правило, являются
полными [3], и поэтому передаточные функции полностью описывают
эти звенья.
Рассмотрим процедуру преобразования структурных схем на основе
моделей в переменных состояния на примере простой системы, струк-
турная схема которой приведена на рис. 3.19.
I II
III
g
g
1
y
1
g
2
y
2
g
3
y
3
y
4
y
Рис. 3.19
Имея ввиду изложенное выше, предположим, что в результате обрат-
ного перехода от передаточных функций
)(
I
pW
,
)(
II
pW
и
)(
III
pW
эле-
ментов к их уравнениям в переменных состояния или каким либо другим
методом, получены следующие полные системы уравнений элементов:
I.
11111
gbxAx +=
&
, II.
22222
gbxAx +=
&
, III.
33333
gbxAx +=
&
,
(3.74)
111
xcy
T
=
,
222
xcy
T
=
,
333
xcy
T
=
.
(3.75)
148
Необходимо найти уравнения системы в переменных состояния вида
bgAxx
+
=
,
dgxcy
T
+=
,
т.е. в (3.74), (3.75) необходимо выделить вход
g
и выход
y
системы,
найти размерность вектора
x
, коэффициенты матрицы
A
, векторов
b
и
T
c
, а также скаляр
d
.
Для решения задачи целесообразно принять следующую последова-
тельность действий:
1. Непосредственно по структурной схеме записать уравнения связи
между элементами.
2. Из уравнений связей, уравнений выходов (3.75), а затем и уравне-
ний состояний (3.74) всех элементов исключить все промежуточные пе-
ременные
,
i
g ,
i
y
K2,1
=
i
так, чтобы эти уравнения содержали только
переменные состояния
i
x
и входные воздействия системы.
3. Объединить векторы переменных состояния звеньев в один вектор
состояния системы путём “прямого” суммирования (см. П.1.30).
4. Записать уравнения состояния всей системы в стандартной форме.
5. Записать уравнения выходов системы.
Перейдём к решению задачи. По структурной схеме системы (рис.
3.19) запишем уравнения связей между элементами с учетом внешних
воздействий
, ,
23441
yyyygg
+=−=
. , ,
21312
yyygyg ===
(3.76)
Переходя к выполнению второго шага, замечаем, что уравнения выхо-
дов
321
,
,
y
y
y
(3.75) не содержат промежуточных переменных, поэтому
их оставляем без изменения. Преобразуем уравнения связей (3.76):
3322234
xcxcyyy
TT
+
=
+
=
;
2233231
xcxcgyygg
TT
−−=−−=
.
Переходим к преобразованию уравнений состояния (3.74). Имеем
)(
223311111
xcxcbgbxAx
TT
+
−
+
=
&
,
или
149
,
1331221111
gbxcbxcbxAx
TT
+−−=
&
,
112222
xcbxAx
T
+
=
&
(3.77)
113333
xcbxAx
T
+
=
&
.
Объединим векторы
321
,, xxx
в один вектор состояния
=
3
2
1
x
x
x
x
,
который представляет собой прямую сумму векторов
1
x
,
2
x
,
3
x
.
Записываем выражения для
x
&
и
y
в матричной форме с учётом вы-
ражений (3.76) и (3.77)
g
b
x
Acb
Acb
cbcbA
x
T
T
TT
+
−−
=
0
0
0
0
1
313
212
31211
&
, (3.78)
xcy
T
]00[
2
=
. (3.79)
В этом выражении произведения
T
ij
cb
являются матрицами. Они
вычисляются следующим образом. Пусть, например,
3
b
– четырёхкомпо-
нентный, а
2
c
– трёхкомпонентный векторы-столбцы, т.е.
[
]
T
bbbbb
433323133
=
,
[
]
T
cccc
232221
2
=
.
Тогда их произведение
T
cb
3
запишется в таком виде
=
234322432143
233322332133
232322232123
231322132113
23
cbcbcb
cbcbcb
cbcbcb
cbcbcb
cb
T
.
150
Матрица A полученной системы (3.78), (3.79), составленная, возмож-
но, из прямоугольных блоков, всегда является квадратной. При этом поря-
док системы, равный размерности вектора состояния
x
, равен
321321
dimdimdimdim nnnxxxxn ++=++==
.
Следовательно, в общем случае
∑
=
=
N
i
ic
nn
1
, (3.80)
где N – число звеньев системы,
i
n
– порядок i-го звена системы.
Формула (3.80) есть аналитическая запись правила порядков. Оно
состоит в следующем.
Правило порядков. Порядок системы всегда равен сумме порядков
всех её элементов.
Нетрудно видеть, что приведенное правило порядков может не вы-
полняться при описанных выше преобразованиях структурных схем с
применением правил переноса точек суммирования и ветвления (из-за
добавления элементов) или же формул для определения передаточных
функций простейших соединений звеньев.
Приведём численный пример вывода уравнений системы в перемен-
ных состояния по её структурной схеме.
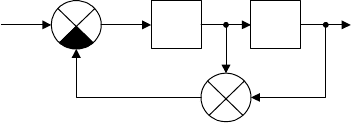
Пример 3.11. Пусть задана система, структурная схема которой
приведена на рис. 3.20.
g y
I II
g
1
y
1
g
2
y
2
y
3
Рис. 3.20
Уравнения её элементов в переменных состояния
111
2
3
31
42
gxx
+
=
&
,
[
]
111
301
gxy
−=
,
