Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.


171
§ 4.2. Случайные векторные процессы
Динамические системы часто подвержены влиянию нескольких слу-
чайных воздействий
)(t
ϕ
. В этом случае соответствующие случайные
процессы объединяют в один вектор-столбец
T
k
tttt ])()()([)(
21
ϕϕϕ=ϕ K
(4.16)
и называют с лу чай ным ве кто рн ым про це ссо м. При этом в (4.16)
все
)(t
i
ϕ
принимают вещественные значения и
0
tt ≥
, где
0
t
– момент
начала наблюдения.
Случайный векторный процесс в целом характеризуется теми же
статистическими характеристиками, что и скалярный процесс, но опре-
деленными для векторных величин. К ним относятся: совместное распре-
деление вероятностей, вектор средних значений, матрица дисперсий, ко-
вариационная матрица и т.д. Если эти характеристики не зависят от вре-
мени, то случайный векторный процесс является стационарным.
Рассмотрим определение указанных характеристик [9]. Вектором
средних значений называется вектор
T
k
tttt ])()()([)(
21
ϕϕϕ=ϕ
K
. (4.17)
Здесь и в дальнейшем черта над функцией обозначает усреднение как в
смысле (4.1), так и в смысле (4.2)
Кова риа цион но й ма тр иц ей случайного векторного процесса
(4.16) называется матрица
T
ttttttR ))()())((()((),(
221121
ϕ−ϕϕ−ϕ=
ϕϕ
. (4.18)
В случае двумерного процесса
T
ttt ])()([)(
21
ϕϕ=ϕ
ковариационная
матрица
),(
21
ttR
ϕϕ
(4.18) имеет вид
=
ϕϕϕϕ
ϕϕϕϕ
ϕϕ
),(),(
),(),(
),(
21
22
21
21
21
12
21
11
21
ttRttR
ttRttR
ttR
, (4.19)
где
))()())((()((),(
2121111121
11
ttttttR ϕ−ϕϕ−ϕ=
ϕϕ
,

172
))()())((()((),(
2222111121
12
ttttttR ϕ−ϕϕ−ϕ=
ϕϕ
,
))()())((()((),(
2121121221
21
ttttttR ϕ−ϕϕ−ϕ=
ϕϕ
,
))()())((()((),(
2222121221
22
ttttttR ϕ−ϕϕ−ϕ=
ϕϕ
.
Если случайный векторный процесс центрирован, т.е.
0)( =ϕ t
i
при
всех
ki ,1=
и t, то выражения (4.18) и (4.19) упрощаются и, в частности
при
2
=
k
, принимают вид
)()(),(
2121
ttttR
T
ϕϕ=
ϕϕ
, (4.20)
или
ϕϕϕϕ
ϕϕϕϕ
=
ϕϕ
)()()()(
)()()()(
),(
22122112
22112111
21
tttt
tttt
ttR
. (4.21)
В случае случайного стационарного векторного процесса, когда ха-
рактеристики не зависят от времени, можно положить
τ+== tttt
21
,
.
Тогда из (4.20) и (4.21) с учётом (4.5) следует
)()(),(),(
21
τ+ϕϕ=τ+=
ϕϕϕϕ
ttttRttR
T
, (4.22)
τ+ϕϕτ+ϕϕ
τ+ϕϕτ+ϕϕ
=τ+
ϕϕ
)()()()(
)()()()(
),(
2212
2111
tttt
tttt
ttR
или
ττ
ττ
=τ
ϕϕϕϕ
ϕϕϕϕ
ϕϕ
)()(
)()(
)(
2212
2111
RR
RR
R
,
2
=
k
. (4.23)
Таким образом, в стационарном случае диагональными элементами
ковариационной матрицы являются обычные автокорреляционные функ-
ции компонентов случайного векторного процесса. Недиагональные эле-
менты ковариационной матрицы представляют собой взаимные корреля-
ционные функции компонентов случайного векторного процесса.
173
Матр иц ей ди сп ер сий случайного векторного процесса называ-
ется матрица
),()( ttRtD
ϕϕϕ
=
. В стационарном случае матрица
constRDtD ===
ϕϕϕϕ
)0()(
.
Пусть
)(t
ϕ
и
)(tψ
два случайных векторных процесса. Тогда
)(t
ϕ
и
)(tψ
называются независимыми или некоррелированными случайными
процессами, если
0),(
21
=
ϕ
ttR
ψ
при всех
012
ttt ≥≥
. Здесь
T
ψ
tψtψttttR ))()())((()((),(
221121
−ϕ−ϕ=
ϕ
. (4.24)
Это определение позволяет ввести, так называемые, сл уча йн ые
пр оце ссы с н еко рр ели ро ван ным и п рир ащ ени ям и. Случайный
векторный процесс
)(t
ν
этого типа определяется следующим образом.
1. Начальное значение процесса
0)(
0
=ν t
.
2. Для любой последовательности моментов времени
4321
,,,
tttt
, где
43210
ttttt ≤≤≤≤
, векторные приращения
)()(
12
tt ν−ν
и
)()(
34
tt ν−ν
имеют нулевые средние и являются некоррелированными, т.е.
0)()()()(
3412
=ν−ν=ν−ν tttt
, (4.25)
0))()())((()((
3412
=ν−νν−ν
T
tttt
. (4.26)
Случайный векторный процесс с некоррелированными прираще-
ниями обладает следующими свойствами [9].
1. Среднее значение процесса равно нулю
0)()()(
0
=ν−ν=ν ttt
,
0
tt ≥
. (4.27)
2. Ковариационная матрица этого процесса совпадает с его матрицей
дисперсий, вычисленной при меньшем значении аргументов
)()()(),(
121
1
tDttttR
tt
T
ν
=
νν
=νν=
,
012
ttt ≥≥
. (4.28)

174
3. Процесс с некоррелированными приращениями не является ста-
ционарным.
4. Матрица дисперсий
)]([)(
1
tdtD
ji
ν
ν
=
является монотонно неубы-
вающей матричной функцией от t, т.е.
)()(
12
tdtd
jiji
νν
≥
для всех
012
ttt ≥≥
. (4.29)
Примером процесса с некоррелированными приращениями является
процесс броуновского движения, часто называемый процессом Винера.
Приращения
)()(
1 ii
tt ν−ν
+
K,3,2,1
=
i
этого процесса являются слу-
чайными гауссовскими векторами с нулевым средним. Броуновское дви-
жение является гауссовским процессом [9].
По аналогии со скалярным белым шумом определяется сл уча йн ый
век то рны й п роц ес с ти па бе ло го шу ма.
Случайный векторный процесс
)(t
ν
с нулевым средним называется
случайным векторным процессом типа белого шума, если его ковариаци-
онная матрица
)()(),(
12112
tttVttR −δ=
νν
, (4.30)
где
)(tV
– ма три ца и нт енси вно ст и процесса
)(t
ν
,
ε>−
12
tt
, где
ε
– «малое» число.
Матр ица сп ек тра ль ны х пло тн ост ей случайного стационар-
ного векторного процесса определяется аналогично (4.7) выражением
ττ=ω
ωτ−
∞
∞−
ϕϕϕϕ
∫
deRS
j
)()(
. (4.31)
матрица
)(ω
ϕϕ
S
является комплексно-значной матрицей и обладает сле-
дующими свойствами
)()( ω=ω−
ϕϕϕϕ
T
SS
, (4.32)
)()( ω=ω
ϕϕ
∗
ϕϕ
SS
, (4.33)
0)( ≥ω
ϕϕ
S
(4.34)
175
для всех
ω
. Здесь
∗
обозначает комплексно-сопряжённое транспонирова-
ние, а неравенство
0)( ≥ω
ϕϕ
S
означает, что
)(ω
ϕϕ
S
является неотрица-
тельно определённой матрицей [11], т. е.
0)( ≥ω
ϕϕ
∗
xSx
при любом век-
торе x и при всех значениях частоты
ω
.
Из выражений (4.30) и (4.31) в частности следует, что матрица спек-
тральных плотностей векторного стационарного белого шума
VS =ω
νν
)(
, (4.35)
то есть совпадает с матрицей его интенсивности и постоянна.
Приведённые в этом параграфе выражения (4.17) – (4.35) свидетель-
ствуют, что свойства и статистические характеристики случайных век-
торных процессов практически полностью аналогичны свойствам и ха-
рактеристикам (4.3) – (4.9) случайных скалярных процессов
§ 4.3. Статистические характеристики выходных
переменных в установившемся режиме
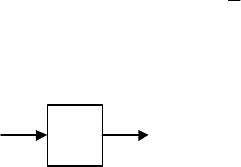
Скалярные воздействия. Рассмотрим линейную, устойчивую ди-
намическую систему (рис. 4.6), на вход которой поступает случайный
стационарный эргодический скалярный процесс
)(t
ϕ
с заданными стати-
ческими характеристиками:
ϕ
,
ϕ
D
,
(
)
τ
ϕϕ
R
и
(
)
ω
ϕϕ
S
. Известно, что в
установившемся режиме выходная переменная такой системы тоже является
случайным стационарным эргодическим процессом [7, 9].
Необходимо найти выражения, определяю-
щие соответствующие статистические характери-
стики выходной переменной
)(ty
рассматривае-
мой системы.
Так как система линейная, то она может
быть задана либо уравнениями в переменных со-
стояния
ϕ
+
=
bAxx
&
, (4.36)
xcy
T
=
. (4.37)
либо передаточной функцией
(
)
(
)
bApEcpW
T
1−
−=
,
W(p)
ϕ
y
Рис. 4.6

176
либо импульсной переходной характеристикой
becpWLtw
AtT
==
−
)]([)(
1
. (4.38)
Найдем выражение для
)(ty
через
)(tw
. Применяя формулу (2.133)
к системе (4.36), (4.37), получим
ττϕ+=
∫
τ−
dbecxecty
t
tATAtT
0
)(
0
)()(
.
Будем рассматривать систему (рис. 4.6) при нулевых начальных ус-
ловиях, т.е. при
0
0
=x
. Тогда с учетом выражения (4.38) получим
∫
ττϕτ−=
t
dtwty
0
)()()(
. (4.39)
Так как
0)(
≡
tw
при
0
<
t
, то в этом выражении можно
t
заменить
на
∞
. Проведем затем замену переменных в (4.39), полагая
1
τ=τ−t
.
Тогда
=
−∞=τ∞=τ
=τ=τ
τ−=ττ=τ−
=ττϕτ−=
∫
∞
,,
,,0
,,
)()()(
1
1
11
0
t
ddt
dtwty
∫
−∞
ττ−ϕτ−=
t
dtw
111
)()(
или
∫
∞
ττ−ϕτ=
0
111
)()()( dtwty
. (4.40)
В соответствии с равенством (4.38) можно записать
∫
∞
−
==
0
)()}({)( dtetwtwLpW
pt
.
Поэтому, заменяя
p
на
ω
j
, получим

177
ττ=ω
ωτ−
∞
∫
dewjW
j
0
)()(
. (4.41)
Среднее значение выхода. Для заданного случайного входного
процесса
)(t
ϕ
(стационарного) его среднее значение
ϕ
является посто-
янной величиной. Поэтому изображение по Лапласу этого среднего зна-
чения имеет вид
pp ϕ=ϕ )(
. Следовательно, по определению переда-
точной функции
ppWpy
ϕ
=
)()(
, т.е.
)}({lim
1
pyLy
t
−
∞→
=
.
Поэтому, применяя теорему о предельном значении, получим
ϕ=
ϕ
===
→→→
∞
)(lim)(lim)(lim
000
pW
p
pWppypyy
ppp
.
Если система устойчива, то
)(pW
не имеет полюсов в точке
0
=
p
.
В этом случае предел существует и равен
ϕ
=
)0(Wy
. (4.42)
Корреляционная функция выхода. Воспользуемся общей форму-
лой (4.5) для корреляционной функции
dttytyR
yy
∫
∞
τ+=τ
0
)()()(
. (4.43)
Подставляя в (4.43) выражения для
)(ty
и
)(
τ
+
ty
из полученного выше
равенства (4.40), будем иметь
dtdtwdtwR
yy 2
0 0
221
0
11
)()()()()( ττ−τ+ϕτττ−ϕτ=τ
∫ ∫∫
∞ ∞∞
.
В этом выражении, как и в (4.5), предполагается, что процессы
)(t
ϕ
и
)(ty
являются центрированными. Если это не так, т.е.
0
≠
ϕ
, то
в этих формулах и в дальнейшем
)(ty
и
)(t
ϕ
обозначают разность вы-
ходной переменной и входного процесса и их средних значений, соот-
ветственно.
178
Так как пределы в интегралах последнего равенства бесконечные,
то интегралы можно переставлять, т.е. менять порядок интегрирова-
ния. Поэтому предыдущее выражение можно представить следующим
образом:
12
0 0
21
0
21
)()()()()( τττ−τ+ϕτ−ϕττ=τ
∫ ∫∫
∞ ∞∞
ddtdttwwR
yy
.
Применяя замену
)()()(
12112
τ−τ−τ+τ+τ−ϕ=τ−τ+ϕ tdtdtt
,
zt =τ−
1
,
dztd =τ− )(
1
,
получим
∫∫ ∫
∞∞ ∞
τττ−τ+τ+ϕϕττ=τ
0
1221
0 0
21
)()()()()( dddzzzwwR
yy
.
Так как по (4.5)
)()()(
21
0
21
τ−τ+τ=τ−τ+τ+ϕϕ
ϕϕ
∞
∫
Rdzzz
,
то окончательно имеем
12
0 0
2121
)()()()( τττ−τ+τττ=τ
∫ ∫
∞ ∞
ϕϕ
ddRwwR
yy
. (4.44)
Взаимная корреляционная функция между входом и выходом. В
соответствии с выражением (4.6) и условием, что
0)(
=
ty
при
0
<
t
,
можно записать равенство
dttytR
y
∫
τ+ϕ=τ
∞
ϕ
0
)()()(
.
Здесь, как и выше, предполагается, что процессы
)(t
ϕ
и
)(ty
являются
центрированными. Поэтому с учетом (4.40) получим
dtdtwtR
y 1
0
11
0
)()()()( τ
∫
τ−τ+ϕτ
∫
ϕ=τ
∞ ∞
ϕ
179
или
1
0
1
0
1
)()()()()( ττ−τ+ϕϕϕτ=τ
∫ ∫
∞ ∞
ϕ
dtdtttwR
y
.
Так как по (4.5)
)()()(
11
0
τ−τ=τ−τ+ϕϕ
ϕϕ
∞
∫
Rdttt
,
то из предыдущего выражения выводим формулу
11
0
1
)()()( ττ−ττ=τ
ϕϕ
∞
ϕ
∫
dRwR
y
. (4.45)
Взаимная корреляционная функция между выходом и входом.
Снова в соответствии с формулой (4.6) записываем
dttdtwdtttyR
y
)()()()()()(
11
0 0
1
0
τ+ϕττ−ϕ
∫ ∫
τ=
∫
τ+ϕ=τ
∞∞∞
ϕ
.
Полагая
)()(
11
τ+τ−τ+ϕ=τ+ϕ tt
, получим
∫∫
∞∞
ϕ
ττ+τ+τ−ϕτ−ϕτ=τ
0
1111
0
1
)()()()( dttwR
y
.
Снова учитывая, что по (4.5)
,)()()(
0
1111
∫
∞
ϕϕ
τ+τ=τ+τ+τ−ϕτ−ϕ Rdttt
имеем
11
0
1
)()()( ττ+ττ=τ
ϕϕ
∞
ϕ
∫
dRwR
y
. (4.46)
Сравнивая это выражение с формулой (4.45), заключаем, что в об-
щем случае
)()( τ≠τ
ϕϕ yy
RR
.
Спектральная плотность выходной переменой. В соответствии с
определением спектральной плотности (4.7) и выражением (4.44) можно
записать

180
∫
=ττ=ω
∞
∞−
ωτ−
deRS
j
yyyy
)()(
ττττ−τ+τ
∫
τ
∫ ∫
τ=
ωτ−
ϕϕ
∞∞
∞−
∞
deddRww
j
1221
0
2
0
1
)()()(
.
Умножим подынтегральное выражение на
)()(
2121
τ−τω−τ−τω jj
ee
. Далее
изменим порядок интегрирования и распределим множители
i
j
e
ωτ
,
приписав их к
)(
i
w τ
. В результате будем иметь
×
∫
τ
∫
τ=ω
∞
ωτ−
∞
ωτ−−
ττ
0
22
0
1
)(
1
21
)()()( dewdewS
jj
yy
∫
∞
∞−
τ−τ+τω−
ϕϕ
ττ−τ+τ deR
j )(
21
21
)(
.
Принимая во внимание равенства (4.41) и (4.7), заключаем, что
)()(
0
1
)(
1
1
ω−=ττ
∫
∞
ωτ−−
jWdew
j
,
∫
∞
ωτ−
ω=ττ
0
22
)()(
1
jWdew
j
,
)()(
)(
21
21
ω=ττ−τ+τ
ϕϕ
∞
∞−
τ−τ+τω−
ϕϕ
∫
SdeR
j
.
Поэтому из предыдущего выражения следует очень часто используемая,
простая и удобная формула
).()()()()()(
2
ωω=ωω−ω=ω
ϕϕϕϕ
SjWSjWjWS
yy
(4.47)
Взаимная спектральная плотность между входом и выходом.
Снова воспользовавшись определением (4.8) и формулой (4.45), получим
∫
∞
∞−
ωτ−
ϕϕ
=ττ=ω deRjS
j
yy
)()(
