Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

151
222
1
0
2
032
100
010
gxx
+
−
=
&
,
[
]
22
102 xy
=
.
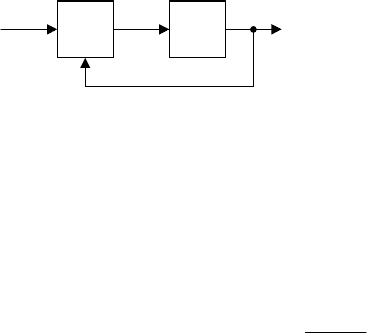
Найти уравнения системы в переменных состояния.
Решение. Уравнения связей, согласно рис. 3.20, имеют вид
,
211
yygg −−=
,
12
yg =
.
2
yy =
Начнём с преобразования уравнений выходов
211121111111
333)(33 yygxcyygxcgxcy
TTT
+++=−−−=−=
.
Перенесём
1
3y
в левую часть
2111
33)31( ygxcy
T
+−=−
.
Отсюда с учетом уравнения выхода
2
y
находим
22111
5,15,15,0 xcgxcy
TT
−+−=
.
Выражение для
222
xcy
T
=
не содержит промежуточных перемен-
ных, поэтому его оставляем без изменения и переходим к преобразовани-
ям уравнений связей. Имеем
2211211
5,05,15,0 xcgxcgyygg
TT
+−+=−−=
.
22112
5,15,15,0 xcgxcg
TT
−+−=
.
Переходим к преобразованиям уравнений в переменных состояния
2211111111111
5,05,0)5,0( xcbgbxcbAgbxAx
TT
+−+=+=
&
Найдём сначала произведения
[ ]
=
=
02
03
01
2
3
11
T
cb
,

152
[ ]
=
=
204
306
102
2
3
21
T
cb
.
Отсюда получаем
=
+
=−
32
45,3
01
05,1
31
42
2
1
111
T
cbA
,
[ ]
=
=
=
102
5, 103
204
306
5, 0102
2
3
5, 05,0
21
T
cb
.
Аналогично
gbxcbxcbAgbxAx
TT
2112222222222
5,15,0)5,1( +−−=+=
&
.
Здесь
[ ]
=
−
−
=− 102
1
0
2
5,1
032
100
010
5,1
222
T
cbA
;
5,135
100
316
5,103
000
306
032
100
010
−−
−−
=
−
−
=
[ ]
−
−
=
−=−
05,0
00
01
01
1
0
2
2
1
2
1
12
T
cb
.
Теперь, объединяя векторы
1
x
и
2
x
в один вектор
x
и записывая
x
&
с учетом полученных выражений и найденных произведений, получим
искомые уравнения системы (рис. 3.20) в переменных состояния
153
gxx
−
−
+
−−−
−−−
=
5,1
0
3
1
5,1
5,13505,0
10000
31601
10232
5,10345,3
&
,
[
]
xy 10200=
.
Отметим, что в соответствии с этими уравнениями порядок рассматри-
ваемой системы равен 5, что соответствует правилу порядков: 5=2+3. Здесь 2
и 3 – порядки элементов
I
и
II
системы, соответственно.
§ 3.6. Полиномиальный метод реализации моделей вход-выход
Рассмотрим следующую задачу теории систем. Структурная схема
динамической системы имеет вид, приведенный на рис. 3.21.
Объект управления (ОУ) задан своим уравнением вход-выход
upBypA )()(
=
. (3.81)
Обозначим
)(deg pAn
=
,
)(deg pBm
=
. Здесь
)deg(
∗
– обо-
значение степени полинома
)(
∗
.
Автоматический регулятор (АР)
описывается своим уравнением вход-выход
ypLgpQypR )()()(
−
=
. (3.82)
Полиномы
)(pR
,
)(pQ
,
)(pL
неизвестны. Их необходимо найти
так, чтобы передаточная функция системы, приведенной на рис. 3.21,
была равна
)(
)(
)(
0
3
pH
pH
pW =
. (3.83)
При этом степени полиномов
)(pQ
и
)(pL
должны удовлетворять
условиям физической реализуемости автоматического регулятора
АР ОУ
g yu
Рис. 3.21

154
,degdeg
*
y
LR µ≥−
,degdeg
*
y
QR µ≥−
(3.84)
где
*
y
µ
– некоторое заданное число (например, 0, 1, 2, 3, …).
Кроме того, коэффициентам полинома
)(pH
в (3.83) можно было
бы назначить любые заранее заданные значения. Степень этого полино-
ма, а также степени полиномов
)(pR
,
)(pQ
и
)(pL
должны быть опре-
делены.
Данная задача, по существу, является задачей реализации переда-
точной функции (3.83) системой с обратной связью (рис. 3.21), у которой
частично задана структура. В этом её отличие от рассмотренной выше
задачи реализации моделей вход-выход динамической системой с произ-
вольной структурой.
Далее рассматривается метод решения этой задачи, и устанавлива-
ются условия существования её решения с учетом условий физической
реализуемости (3.84) динамических звеньев, которые используются при
построении реализующей системы.
Решение этой задачи сводится к решению так называемых полино-
миальных уравнений, которые выводятся следующим образом.
С помощью рассмотренных выше правил преобразования структур-
ных схем можно установить, что передаточная функция с входа
g
на
выход
y
системы, схема которой приведена на рис. 3.21, равна
)()()()(
)()(
)(
pLpBpRpA
pQpB
pW
з
+
=
. (3.85)
Приравнивая (3.83) и (3.85) получим равенства:
)()()(
0
pHpQpB =
, (3.86)
)()()()()( pHpLpBpRpA
=
+
. (3.87)
В этих выражениях полиномы
)(pA
и
)(pB
заданные. Полиномы
)(pH
и
)(
0
pH
тоже могут рассматриваться как заданные, но при неко-
торых условиях. Полиномы
)(pQ
,
)(pR
и
)(pL
в этих уравнениях яв-
ляются неизвестными. Поэтому равенства (3.86) и (3.87) являются поли-
номиальными уравнениями относительно этих полиномов.
Рассмотрим решение полиномиального уравнения (3.87). Так как в
левой и правой части (3.87) полиномы, то это уравнение обратится в тож-
дество, если только степени полиномов правой и левой части будут оди-
155
наковы, а также, если будут равны коэффициенты при одинаковых сте-
пенях переменной
p
в левой и в правой части этого равенства. Предпо-
ложим полиномы в (3.86) и (3.87) имеют вид
01
1
1
)( α+α++α+α=
−
−
ppppA
n
n
n
n
K
,
01
1
1
)( β+β++β+β=
−
−
ppppB
m
m
m
m
K
,
01
1
1
)( ρ+ρ++ρ+ρ=
−
−
ppppR
r
r
r
r
K
,
01
1
1
)( λ+λ++λ+λ=
−
−
ppppL
l
l
l
l
K
,
01
1
1
)( χ+χ++χ+χ=
−
−
ppppQ
q
q
q
q
K
,
01
1
1
)( η+η++η+η=
−σ
−σ
σ
σ
ppppH K
. (3.88)
Обычно выполняются следующие неравенства
n
m
≤
, (3.89)
0≥µ
y
. (3.90)
Здесь величина
}degdeg;degmax{deg QRLR
y
−−=µ
называет-
ся индексом автоматического регулятора АР, заданного уравнением (3.82).
Степень полинома в левой части (3.87) с учетом условий (3.89) и
(3.90) равна
σ
=
+
r
n
. Поэтому степень полинома
)(pH
должна быть
n
r
+
=
σ
. (3.91)
Чтобы решить полиномиальное уравнения его обычно сводят к сис-
теме линейных алгебраических уравнений.
Для изучения методики перехода от полиномиальных к алгебраиче-
ским уравнениям рассмотрим пример.
Пример 3.12. Предположим, полиномы в уравнении (3.87) имеют
следующий вид
01
2
2
)( α+α+α= pppA
,
01
)( β+β= ppB
,
01
)( ρ+ρ= ppR
,
0
)( λ=pL
,
01
2
2
3
3
3
0
3
)()( η+η+η+η=
−η=
∏
=
ppppppH
j
i
,
где
i
p
– желаемые корни
)(pH
. Представить уравнение (3.87) с данны-
ми полиномами в виде системы алгебраических уравнений.
156
Решение. Перемножим заданные полиномы в соответствии с урав-
нением (3.87). В результате получим
3
12
2
1102011000
)()()()( ppppRpA ρα+ρα+ρα+ρα+ρα+ρα=
,
.)()(
0100
ppLpB λβ+λβ=
Теперь, подставляя в (3.87) эти произведения и полином
)(pH
,
приравняем коэффициенты при одинаковых степенях
0
p
,
1
p
,
2
p
,
3
p
в
левой и правой частях этого уравнения. В результате получим
00000
)(
η=λβ+ρα
,
1010110
)(
η=λβ+ρα+ρα
,
21102
)(
η=ρα+ρα
,
312
η=ρα
.
Полученные равенства удобно представить в матричной форме, вы-
делив неизвестные коэффициенты полиномов R(p) и L(p) в вектор неиз-
вестных. В результате придем к следующей системе алгебраических
уравнений
η
η
η
η
=
ρ
ρ
λ
⋅
α
α
α
α
α
α
β
β
3
2
1
0
1
0
0
2
1
0
2
1
0
1
0
0
00
0
. (3.92)
Таким образом, полиномиальное уравнение (3.87) при указанных
выше полиномах
)(
pA
,
)(
pB
,
)(
pR
,
)(
pL
и
)(
pH
эквивалентно сис-
теме алгебраических уравнений типа (3.92). Матрица этой системы, как
видно из (3.92), составляется из коэффициентов полиномов
)(
pA
и
)(
pB
, причем
1
+
l
ее столбцов составляются из коэффициентов поли-
нома
)(pB
, а
1
+
r
столбцов – из коэффициентов полинома
)(pA
. Ко-
эффициенты каждого столбца располагаются в порядке возрастания ин-
декса. В последующих столбцах коэффициенты сдвигаются вниз на одну
строку. Число строк равно
1
+
+
rn
, а число столбцов
11
+
+
+
rl
.
Неизвестными в этой системе являются коэффициенты полиномов
)(pL
и
)(pR
. Они образуют вектор неизвестных. В правой части систе-
157
мы (3.92) стоит вектор, образованный из коэффициентов полинома
)(pH
. Данная система имеет решение, если число неизвестных не
меньше числа уравнений, и если ранг матрицы расширенной системы
равен рангу исходной матрицы [10]. Когда матрица этой системы квад-
ратная, то система имеет решение, если определитель матрицы системы
не равен нулю. Первое из этих условий обеспечивается выбором значе-
ний степеней
r
и
l
полиномов
)(pR
и
)(pL
. Выполнение второго ус-
ловия зависит от свойств полиномов
)(pA
и
)(pB
.
Теорема. Если полиномы
)(pA
и
)(pB
не имеют общих нулей и
матрица системы (3.92), составленная из коэффициентов этих полиномов
квадратная, то её определитель не равен нулю.
Будем считать, что полиномы
)(pA
и
)(pB
в уравнении (3.87) не
имеют общих нулей. Перейдём к выбору значений степеней полиномов
)(pR
и
)(pL
. Условием для этого является неравенство
yн
NN ≥
, где
н
N
– число неизвестных; а
y
N
– число уравнений в системе типа (3.92).
В соответствии с обозначениями (3.88) по условиям (3.90), (3.91) имеем
2++= rlN
н
,
*
y
rl µ−=
,
11 ++=+σ= rnN
y
,
*
22
yн
rN µ−+=
.
Отсюда следует, что условие
y
н
NN ≥
будет выполнено, если
122
*
++≥µ−+ rnr
y
,
то есть, если
*
1
y
nr µ+−≥
. (3.93)
Правая часть этого неравенства определяет минимальное значение
r
, при котором полиномиальное уравнение (3.87) имеет решение.
Обычно берут
*
1
y
nr µ+−=
. (3.94)

158
Чаще всего
0
*
=µ
y
, и тогда
1
−
=
nr
.
После определения значения
r
, т.е. степени полинома
)(pR
, сте-
пени полиномов
)(pL
и
)(pQ
будут равны
*
y
rl µ−=
, (3.95)
*
y
rq µ−≤
. (3.96)
Если степени полиномов
)(pR
,
)(pL
и
)(pH
определяются по
формулам (3.93), (3.94), (3.95) и (3.91), то с учетом обозначений (3.88)
система, эквивалентная уравнению (3.87), имеет вид
η
η
η
η
=
ρ
ρ
λ
λ
⋅
αβ
ααββ
ααββ
αβ
σ
M
M
M
M
LMLM
LMLM
LMMLMM
LL
LL
LL
2
1
0
0
0
1212
0101
00
00
00
r
l
nm
. (3.97)
Матрица этой системы, как видно, имеет
1
+
l
столбцов, составлен-
ных из коэффициентов полинома
)(pB
, и
1
+
r
столбцов, составленных
из коэффициентов полинома
)(pA
.
Если полиномы
)(pB
и
)(pA
не имеют общих нулей или множи-
телей, то система (3.97) имеет решение, которое однозначно определяет
все коэффициенты полиномов
)(pR
и
)(pL
. При этом коэффициенты
полинома
)(pH
, имеющего степень
∗
µ+−
y
n 12
, могут иметь любые
заранее заданные численные значения.
Перейдем к решению полиномиального уравнения (3.86). Полином
)(pB
можно представить в виде
)(pB
m
β
, где
m
β
− коэффициент при
m
p
этого полинома. Поэтому уравнение (3.86) можно записать в виде
)()()(
0
pHpQpB
m
=β
.
159
Так как полином
)(pB
по условиям задачи задан, то данное урав-
нение разрешимо, если только
)(
~
)()(
00
pHpBpH =
. (3.98)
Здесь
)()()(
1
1
pВpppB
m
m
i
B
i
−
=
β=
∏
−=
,
где
B
i
p
– нули полинома
)(pB
, а
)(
~
0
pH
– некоторый полином, степень
которого меньше, чем степень полинома
)(
0
pH
на величину
m
.
Таким образом, равенство (3.98) является условием разрешимости
уравнения (3.86). При выполнении этого условия полином
m
pH
pQ
β
=
)(
~
)(
0
. (3.99)
Из равенств (3.91), (3.86) и (3.96) следует, что индекс
)(deg)(deg
0
pHpH
c
−=µ
задаваемой передаточной функции
)(pW
З
(3.83) замкнутой системы должен удовлетворять неравенству
∗
µ+µ≥µ
yc 0
, (3.100)
где
)(deg)(deg
0
pBpAmn
−=−=µ
– индекс заданного объекта
управления (см. рис. 3.21).
Подчеркнём, что выражения (3.98), (3.100) являются, фактически,
условиями физической реализуемости передаточной функции (3.83) при
заданном объекте (3.81), заданном индексе
∗
µ
y
устройства управления
(3.82), а также при условии, что полиномы
)(pA
и
)(pB
в уравнении
(3.81) не имеют общих нулей.
Если выполнено условие (3.100) и в (3.81)
const)(
0
=β=
pB
, то ус-
ловие (3.98) и условие приведенной выше теоремы выполняются всегда,
т.е. в этом случае уравнения (3.86) и (3.87) всегда разрешимы, причем
матрица в системе (3.97) является треугольной, и эта система разрешает-
ся рекуррентно, снизу вверх.
Подчеркнем, что если в (3.81)
const)(
0
=β=
pB
, то условиями
реализуемости произвольной передаточной функции (3.83) системой,
схема которой приведена на рис. 3.21, являются условие (3.100), а так же

160
неравенство
∗
µ+−≥σ
y
n 12
.
Для большей наглядности рассмотренного здесь полиномиального
метода реализации некоторой передаточной функции системой с частич-
но заданной структурой приведём численный пример.
Пример 3.13. Найти полиномы уравнения (3.82) автоматического
регулятора с
0=µ
∗
y
, при котором система (рис. 3.21) будет иметь пере-
даточную функцию
81210
812
)(
23
+++
+
=
ppp
p
pW
з
, (3.101)
если уравнение объекта (3.81) в операторной форме имеет вид
)(4)()3(
2
pupypp =+
. (3.102)
Решение. В данном случае полиномы:
,812)(
0
+= ppH
,81210)(
23
+++= ppppH
,4)(
=
pB
,3)(
2
pppA +=
степени
,2
=
n
,0
=
m
а коэффициент
.4
0
=β=β
m
Индексы
,213 =−=µ
c
,202
0
=−=µ
т.е. условия (3.98) и (3.100) выполняются, так как
constpB
=
=
4)(
, а
0=µ
∗
y
. Следовательно, задача имеет решение.
Переходя к определению полиномов, по (3.99) находим
.234/)812()(
+
=
+
=
pppQ
Далее по (3.94), (3.95)
,1012
=
+
−
=
r
.101
=
−
=
l
Следовательно, система (3.97) с учетом обозначений (3.88) в
данном случае имеет вид
.
1
10
12
8
1000
3100
0340
0004
1
0
1
0
=
ρ
ρ
λ
λ
⋅
Решение этой системы
,1
1
=ρ
,7
0
=ρ
,4/94/)2112(
1
−=−=λ
2
0
=λ
приводит к полиномам
,7)(
+
=
ppR
.225,2)(
+
−
=
ppL
Таким образом, автоматический регулятор (3.82) в данном случае
описывается уравнением
