Гайдук А.Р. Непрерывные и дискретные динамические системы

Подождите немного. Документ загружается.

131

менных состояния динамических систем, то легко придти к выводу, что

эти схемы не содержат элементов других типов.

Отсюда вытекает чрезвычайно важный для практики вывод. Если

сигналы в системе низкочастотные, то ее модель в переменных состояния

вида (3.1), (3.2) (разумеется, с ограниченными коэффициентами) всегда

физически реализуема. Другими словами, для такой модели можно все-

гда построить электронную схему, уравнения которой будут совпадать с

заданными уравнениями (3.1), (3.2) (с приемлемой для практики точ-

ностью).

В этом смысле и говорят, что уравнения в переменных состояния

всегда физически реализуемы.

Совершенно иная ситуация в случае задания системы моделями вход-

выход. Так как различные виды моделей вход-выход эквивалентны друг

другу, то задачу реализации моделей вход-выход будем рассматривать

применительно к передаточным функциям и передаточным матрицам.

Поскольку модели в переменных состояния всегда физически реали-

зуемы, то можно заключить, что если от модели вход-выход можно пе-

рейти к эквивалентной модели в переменных состояния, то данная мо-

дель вход-выход фи зич ески р еал изу ема. В противном случае модель

вход-выход будет н ер еа ли зу емо й.

Условия физической реализуемости. В случае одномерной систе-

мы, которая задана передаточной функцией, скажем, вида

,)(

α++α+α

β++β+β

(3.60)

переход к эквивалентным уравнениям в переменных состояния возмо-

жен, как показано выше, если только выполняется условие (3.16), т.е.

если

≤

В противном случае указанный переход невозможен. Именно по-

этому условие (3.16) называется условием физической реализуемости

моделей в форме передаточных функций.

Соответствующие системы уравнений в переменных состояния, на-

пример, в виде (3.36), (3.37) или (3.38), (3.39) часто называют р еали за-

ци ей передаточных функций (3.33), (3.34) или (3.60).

Здесь, конечно, есть некоторая условность, так как реализацией, в

прямом смысле этого слова, является именно физическая система (элек-

тронная, механическая или другого типа), уравнения в переменных со-

стояния которой приводят к заданной передаточной функции или задан-

ному уравнению вход-выход.

132

Многомерная система обычно задается своей

передаточной мат-

рицей

)(pW

, элементы которой – скалярные передаточные функции

)(

являются отношением полиномов

)(pB

)(pA

степеней

соответственно.

Условием физической реализуемости указанной

передаточной

матрицы являются неравенства

kjqinm

ijij

,1,,1, ==≤

. (3.61)

Условия (3.61) можно записать в виде (3.16), если обозначить

.,1,,1),(degmax kjqipAnmm

====

(3.62)

Здесь

)(/)()()(;)}({)(;)(deg pApApBpBpAHOKpApBm

ijijijij

===

Итак, передаточная функция или

передаточная матрица

физи ческ и реа лиз уе мы, если они удовлетворяют условиям (3.16)

или (3.61).

Соответствующая система в переменных состояния вида (3.1), (3.2),

передаточная функция (матрица) которой равна заданной, называется

ре али зац ией данной передаточной функции (матрицы).

Например, уравнения (3.51), (3.52) являются реализацией переда-

точной матрицы (3.47), а уравнения (3.27) – реализацией уравнения вход-

выход (3.26) или передаточной функции (3.28).

Минимальная реализация. Как показано выше, одной и той же пе-

редаточной функции или матрице могут соответствовать различные сис-

темы уравнений в переменных состояния. Причем эти системы-

реализации отличаются друг от друга как переменными состояния, фор-

мой и коэффициентами матриц, так и порядком. С увеличением порядка

модели возрастает сложность соответствующей физической системы, т.е.

число интеграторов, сумматоров, усилителей и других элементов в ее со-

ставе.

В связи с этим вводится понятие минимальной реализации.

133

Ми ни ма льной р еа ли за ци ей данной передаточной матрицы

(функции) называется система уравнений в переменных состояния вида

(3.1), (3.2) наименьшего порядка, передаточная матрица (функция) кото-

рой равна заданной.

Отметим, что минимальная реализация также не является единст-

венной. Однако все минимальные реализации одной и той же передаточ-

ной матрицы (функции) имеют один и тот же порядок.

Например, системы уравнений (3.41), (3.42) и (3.43), (3.44) являются

минимальными реализациями передаточной функции (3.40), и обе они

имеют третий порядок. В то же время система (3.45), (3.46) также являет-

ся реализацией передаточной функции (3.40). Однако эта система не яв-

ляется минимальной реализацией, так как ее порядок равен четырем.

Аналогично, система уравнений (3.58), (3.59) является минимальной

реализацией передаточной матрицы (3.57), а система

gxx

























−−

430

100

010

gxy

























−−

24240

651

ее реализацией, которая не является минимальной.

Подчеркнем, что здесь рассматривается физическая реализация всей

системы, которая задана своей моделью вход-выход. Если же часть сис-

темы уже существует, то задача реализации модели вход-выход такой

системы и соответствующие условия физической реализуемости значи-

тельно сложнее. Этот случай рассматривается ниже.

§ 3.4. Преобразование структурных схем

Одной из разновидностей моделей динамических систем являются

структурные схемы. Особенно удобны структурные схемы для описания

или задания сложных систем, состоящих из множества взаимодействую-

щих, взаимосвязанных элементов.

В общем случае структурная схема системы, отображающая состав

ее элементов и связей между ними, представляет собой достаточно слож-

ную конфигурацию. Анализ системы по такой структурной схеме затруд-

нителен. На практике сложные структурные схемы путем эквивалентных

преобразований приводят к простейшему виду. Такая схема имеет один –

134

три элемента, и непосредственно по ней можно записать или легко найти

передаточные функции или же одно или несколько уравнений, описы-

вающих систему. Исследование этих уравнений или их решений, как по-

казано во второй главе, дает возможность установить свойства исследуе-

мой системы.

В данной главе изучаются именно такие эквивалентные преобразо-

вания структурных схем.

Определение передаточных функций простейших соединений

элементов. В любой сложной структурной схеме всегда можно выделить

отдельные фрагменты, в которых элементы соединены или последовательно

друг с другом, или параллельно, или в виде обратной связи.

В связи с этим рассмотрим сначала правила эквивалентных преобра-

зований указанных простейших соединений, т.е. выведем формулы, по

которым определяются передаточные функции этих соединений по пере-

даточным функциям отдельных элементов. Зная передаточную функцию

некоторого соединения, все элементы между входом и выходом этого

соединения на схеме системы можно заменить одним элементом с пере-

даточной функцией соединения. Ясно, что при такой замене структурная

схема видоизменяется, становится более простой. Говорят, схема – пре-

образуется, а соответствующие формулы называются формулами эквива-

лентных преобразований.

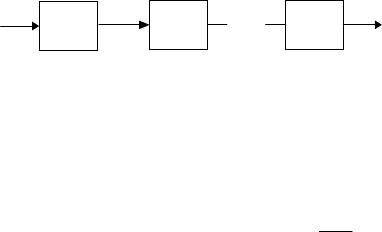
Последовательное соединение. Структурная схема данного соеди-

нения приведена на

рис. 3.6. Для краткости

здесь и в дальнейшем

аргумент

в записи

передаточной функции

)(pW

на рисунках

опущен. Входная переменная соединения обозначена g, а выходная –

Причем, как видно на рис. 3.6,

gg =

, а

yy =

Непосредственно по схеме на рис 3.6 можно записать уравнения по-

следовательного соединения

1−

,2=

. (3.63)

Далее, последовательно подставляя в равенство

)()( pypy

вы-

ражения для выходных переменных звеньев

)()()( pgpWpy

iii

, полу-

чим с учётом выражения (3.63):

...

Рис. 3.6

135

−−−

)()()()()()()()()(

111

pgpWpWpypWpgpWpypy

nnnnnnnn

).()( )()(

pgpWpWpW

−

Отсюда следует, что передаточная функция последовательного со-

единения

)(pW

определяется выражением

∏

)(

. (3.64)

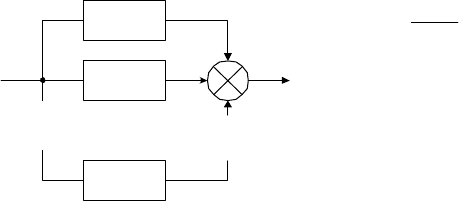
Параллельное соединение.

Схема этого соединения приведена

на рис.3.7. Обозначения здесь те

же, что и на рис. 3.6. Непосредст-

венно по схеме записываются

уравнения

∑

Отсюда, с учетом равенств

)()()( pgpWpy

iii

, следует выражение

).()()()()(

pgpWpgpWpy













∑

(3.65)

На основе (3.65) заключаем, что передаточная функция параллель-

ного соединения определяется формулой

∑

pWpW

)()(

. (3.66)

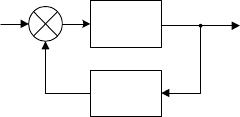
Соединение в виде обратной связи. Соединение в виде обратной

связи – это такое соединение, когда выход одного (первого) элемента

соединяется с входом другого, а выходная переменная этого другого эле-

мента алгебраически суммируется (т.е. со знаком “+” или “–”) с входной

переменной первого звена. При этом входной переменной (входом) дан-

ного соединения является та переменная, с которой происходит алгеб-

раическое суммирование, а выходной – выходная переменная первого

звена. Схема этого соединения приведена на рис. 3.8. Принято ветвь

ygg →→

называть прямой связью, а ветвь

ygy →→

– обратной

связью.

...

g y

Рис. 3.7

136

Переменная

ос

называется выходом обратной связи, а звено

)(pW

ос

– звеном обратной связи. Звено

)( pW

называют иногда прямой

связью.

Если сигнал обратной связи

ос

складывается с входным сигналом

соединения

, т.е. если

ос

ygg +=

, (3.67)

то обратная связь называется положительной.

Если же сигнал обратной связи

ос

вычитается из входного сигна-

ла, т.е. если

ос

ygg −=

, (3.68)

то обратная связь называется отрицательной.

Эти уравнения (3.67) и (3.68) назы-

ваются уравнениями замыкания. В от-

личие от предыдущих соединений в

данном случае в результате введения

обратной связи возникает замкнутый

контур распространения сигналов, что

принципиально изменяет свойства со-

единения по сравнению со свойствами

отдельных звеньев

)( pW

)(pW

ос

Непосредственно по схеме на рис. 3.8 можно записать

)()(

pgpWy

)()()(

pgpWpy

осос

)()()(

pypgpg

ос

±=

Далее, исключая, как обычно, промежуточные переменные

ос

найдем

))()()(()()()()(

211

pgpWgpWpgpWpypy

оспп

±===

)()()()()()( pypWpWpgpWpy

оспп

±=

или

)()()())()(1( pgpWpypWpW

пocп

ос

Рис. 3.8

137

Следовательно, при положительной обратной связи (ПОС) переда-

точная функция соединения определяется выражением

)()(1

)(

pWpW

осп

−

. (3.69)

Аналогично, при отрицательной обратной связи (ООС)

)()(1

)(

pWpW

осп

. (3.70)

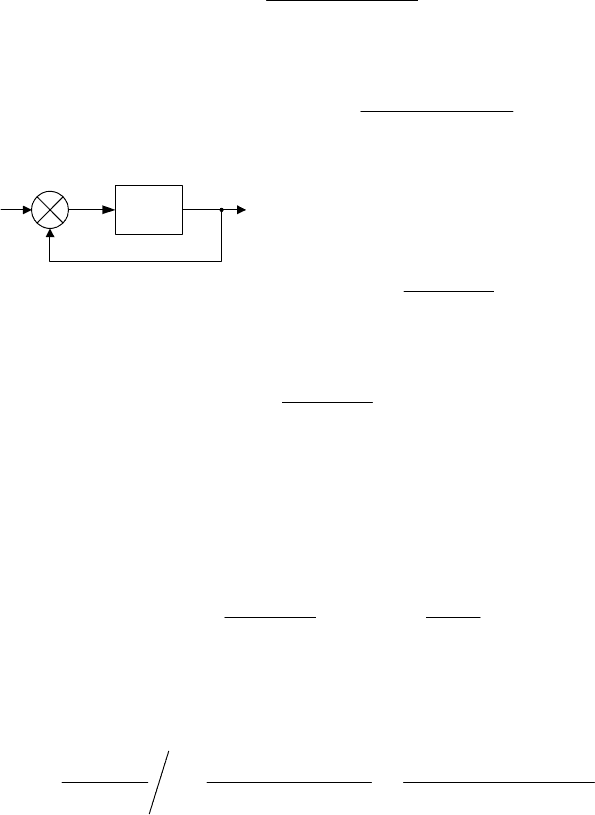
В случае единичной обратной

связи, показанной на рис. 3.9, форму-

лы (3.69) и (3.70) принимают вид:

– при единичной ПОС

( )

)(1

)(

−

, (3.71)

– при единичной ООС

)(1

)(

. (3.72)

Полученные выше формулы (3.64), (3.67), (3.69) – (3.72) очень ши-

роко используются при исследовании динамических систем, и в частно-

сти, систем автоматического управления.

Пример 3.7. Найти передаточную функцию соединения с отрица-

тельной обратной связью (см. рис. 3.8), если

5,0

)(

ос

Решение. Так как связь отрицательная и неединичная, то, вос-

пользовавшись формулой (3.70), найдем после очевидных преобра-

зований

205,35,1

1030

)13)(5,0(

210

5,0

)(

2322

+++













⋅

ppp

ppppp

Рис. 3.9

138

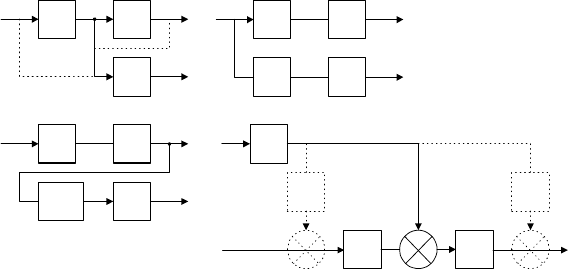
Правила переноса точек суммирования и ветвления. Перед при-

менением приведенных выше формул простейших соединений в слож-

ных структурных схемах часто целесообразно сначала перенести точки

ветвления (узлы) или точки суммирования. Перенос уз лов показан на

рис. 3.10,а. Перенос точ ек сум мир ова ния – на рис. 3.10,г.

Чтобы выходные сигналы преобразуемого участка не изменились, не-

обходимо включать дополнительные звенья, как показано на рис. 3.10,б, рис.

3.10,в или рис. 3.10,г. При таком преобразовании передаточные функции

связей

yg →

не изменяются, в чем не трудно

убедиться, применив формулу (3.64) к схемам на рис. 3.10.

−

а)

в) г)

б)

−

Рис. 3.10

При определении передаточных функций дополнительных звеньев,

которые включаются в схему после переносимого узла или перед перено-

симой точкой суммирования, необходимо руководствоваться следующим

общим правилом.

Правило эквивалентных переносов узлов или точек суммирова-

ния. Выходная переменная преобразуемого участка структурной схемы

после преобразования должна быть равна выходной переменной этого же

участка до преобразования.

Последовательное применение данного правила совместно с рас-

смотренными выше формулами для передаточных функций простейших

соединений элементов позволяет, как показано ниже, привести любую

сколь угодно сложную структурную схему к простой, содержащей один

или несколько элементов.

139

Метод последовательных преобразований структурных схем.

Этот метод упрощения структурных схем заключается в последователь-

ной замене отдельных фрагментов структурной схемы эквивалентным

звеном, в соответствии с формулами для передаточных функций про-

стейших соединений. Для обеспечения возможности применения этих

формул обычно осуществляется перенос точек суммирования или ветв-

ления. Основными сложностями этого метода являются, во-первых, не-

обходимость многократного изображения преобразованных на промежу-

точных этапах структурных схем, а во-вторых, неопределенность того, с

переноса какого узла или какой точки суммирования целесообразно на-

чинать преобразования. В большинстве случаев это не имеет большого

значения, но в некоторых случаях неудачный "перенос" приводит к вари-

анту схемы, дальнейшее преобразование которого становится невозмож-

ным. В таких случаях приходится возвращаться к исходной структурной

схеме, и начинать преобразование с переноса другой точки.

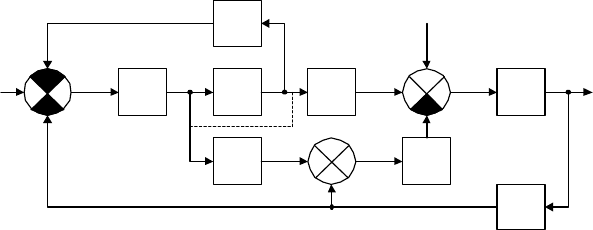
Пример 3.8. Рассмотрим этот метод на примере упрощения струк-

турной схемы, приведенной на рис. 3.11.

Рис. 3.11

Решение. Несмотря на большое количество элементов, ни одну из

приведенных выше формул нельзя применить непосредственно к фраг-

ментам исходной схемы. Поэтому перенесем сначала узел

через звено

и узел

. Добавив необходимое в соответствии с общим правилом

переноса точек звено

−

, получим новую структурную схему, приве-

денную на рис. 3.12.

На этой схеме блоки

−

образуют последовательные

соединения. Заменим эти блоки эквивалентными

140

319

WWW =

310

WWW

−

В результате первой замены получается соединение

с отрица-

тельной обратной связью. Заменим его блоком

−

Рис. 3.12

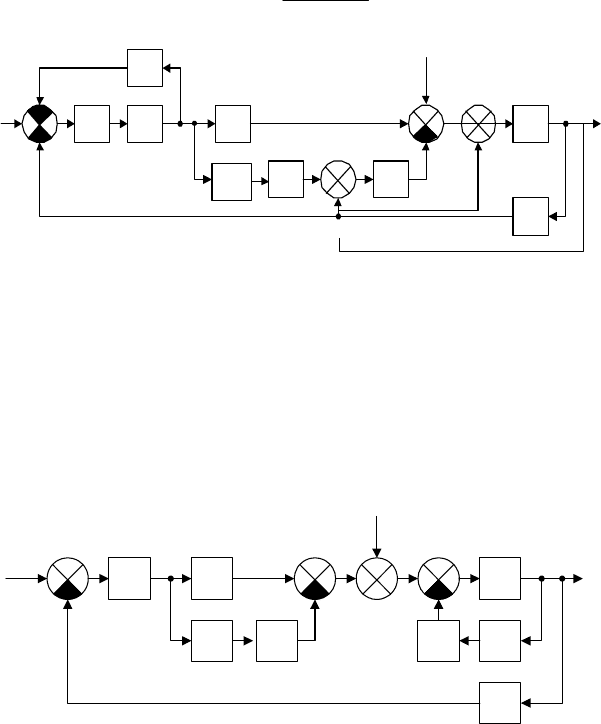
С целью дальнейшего упрощения схемы (рис. 3.12) перенесем точку

суммирования "

" через блок

и точку суммирования "

", а точку

ветвления "

" перенесем через блок

, как показано штриховыми ли-

ниями на рис. 3.12. После этого разделим точку суммирования "

" на

две, отделив суммирование выходного сигнала блока

и возмущения

. В результате описанных преобразований схема на рис. 3.12 примет

вид, показанный на рис. 3.13.

Рис. 3.13