Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

181
=τττ−ττ=
∫ ∫
∞
∞−
∞
ωτ−ωτ
ωτ−
ϕϕ
0
111
11
)()(
jj
j
eededRw
.)()(
)(
1
0
11
11
∫∫
∞
∞−
τ−τω−
ϕϕ
∞
ωτ−
ττ−τττ= deRdew
jj
В соответствии с равенствами (4.41) и (4.7)
∫
∞
ωτ−
ττ=ω
0
11
1
)()( dewjW
j
,
∫
∞
∞−
τ−τω−
ϕϕϕϕ
ττ−τ=ω deRS
j )(
1
1
)()(
,
поэтому
)()()(
ω
ω
=
ω
ϕϕϕ
SjWjS
y
. (4.48)
Аналогично можно показать, что
(
)
(
)
(
)
.
ω
ω
−
=
ω
ϕϕϕ
SjWjS
y
(4.49)
Векторные воздействия. Перейдём к определению статистических
характеристик выходных переменных динамических систем в устано-
вившемся режиме в случае случайных векторных воздействий.
При этом будем предполагать, что рассматриваемая система (рис.
4.6), является многомерной, т.е. имеет несколько входов и несколько вы-
ходов. Причем прямая связь между входами и выходами отсутствует. В
этом случае уравнения системы в переменных состояния (см. параграф
1.2) имеют вид
ϕ
+
=
BAxx
&
, (4.50)
Cxy
=
, (4.51)
где
)(txx
=
,
)(t
ϕ
=
ϕ
и
)(tyy
=
– векторы, а A, B и C – матрицы соот-
ветствующих размерностей.
Формула (2.133), определяющая выходную величину некоторой ди-
намической системы, применительно к системе уравнений (4.50), (4.51)
при нулевых начальных условиях принимает вид аналогичный (4.39)

182
ττϕτ−=
∫
dtWty
t
t
0
)()()(
, (4.52)
где
)(tW
– матриц а и мп уль сных пе рех од ных фу нкц ий . Каждый
i-й столбец этой матрицы представляет собой реакцию системы (4.50),
(4.51) на входной вектор
)(t
ϕ
, у которого i-я компонента является дель-
та-функцией, т.е.
)()(
0
ttt
i
−δ=ϕ
, а остальные равны нулю.
По аналогии с выражением (4.38) можно записать
BCepWLtW
tA
==
−
)}({)(
1
, (4.53)
где
)(pW
– передаточная матрица (см. параграф 3.1) динамической сис-
темы (4.50), (4.51).
Переходя к определению искомых характеристик, прежде всего, от-
метим, что выходная величина
)(tyy
=
(4.52) системы (4.50), (4.51) фак-
тически является реализацией некоторого случайного векторного процес-
са. Поэтому, применяя сначала операцию усреднения к выражению
(4.52), найдем, что вектор средних значений выходного процесса
)(ty
определяется выражением
.)()()()()(
00
∫∫
ττϕτ−=ττϕτ−=
t
t
t
t
dtWdtWty
(4.54)
Аналогично соотношению (4.44) для скалярного случая, из выраже-
ния (4.52) и определений (4.18), (4.23) следует, что если процесс
)(t
ϕ
=
ϕ
является случайным стационарным векторным процессом, то
ковариационная матрица выхода динамической системы, являющегося
тоже случайным стационарным векторным процессом, определяется [9]
равенством
2122121
0 0
121
)()()()( ττττ−τ+−τ=−
ϕϕ
∞∞
∫ ∫
ddWttRWttR
T
yy
. (4.55)
Здесь предполагается, что соответствующие интегралы существуют.
Подвергая, как и в скалярном случае, преобразованию Фурье выра-
жение (4.55), получим формулу для определения матрицы спектральной
плотности выходного случайного векторного стационарного процесса

183
)()()()( ω−ωω=ω
ϕϕ
jWSjWS
T
yy
, (4.56)
где
)(
ω
jW
– комплексная передаточная матрица динамической системы
(4.50), (4.51), а
)(ω
ϕϕ
S
– спектральная матрица случайного входного
векторного процесса
)(t
ϕ
=
ϕ
.
Из выражений (4.10) и (4.56) следует формула
ωω−ωω
π
=
ϕϕ
∞
∞−
∫
djWSjWD
T
y
)()()(
2
1
. (4.57)
Нетрудно видеть, что соотношения (4.54) – (4.57) полностью анало-
гичны соответствующим равенствам (4.42), (4.44) и (4.47) в скалярном
случае. Подчеркнем, что указанные соотношения позволяют определить
статистические характеристики выходных переменных линейных дина-
мических систем в установившемся режиме, т.е. по истечении времени
переходного процесса, после начала функционирования системы.
§ 4.4. Переходные процессы при случайных воздействиях
Перейдем к анализу влияния случайных воздействий на линейные
динамические системы в переходных режимах.
Предварительно рассмотрим некоторые свойства случайных вектор-
ных процессов типа белого шума.
Пусть
)(t
ν
– случайный векторный процесс типа белого шума с мат-
рицей интенсивности
)(tV
, а
)(
1
tA
,
)(
2
tA
и
)(tA
– заданные детермини-
рованные, переменные матрицы. Тогда справедливы соотношения [9]
0)()(
2
1
=
ν
∫
t
t
dtttAM
,
=
∫
ττντ
∫
ν
4
3
2
1
)()()()(
21
t
t
T
t
t
dAQdtttAM
∫
=
I
T
dttQAtAtVtr )]()()([
2
1
, (4.58)

184
где I – пересечение интервалов
],[
21
tt
и
],[
43
tt
, а Q – симметрическая
положительно определённая (см. П.6.3) (весовая) матрица;
][
⋅
tr
– след
матрицы
][
⋅
(см. П.5.11);
∫
=
∫
ν
∫
ν
I
Т
Т
t
t
t
t
dttAtVtAdtttAdtttAM )]()()(')'()'()()(
2
1
21
4
3
2
1
.
(4.59)
Соотношения (4.54) – (4.59) используются обычно при исследовании
влияния случайных векторных воздействий на различные системы.
Далее рассмотрим некоторую линейную динамическую систему с
постоянными параметрами, на вход которой поступает случайный век-
торный процесс типа белого шума [9]. Уравнение состояний системы
аналогично соотношению (4.50) и имеет вид
)()()( tBtAxtx
ν
+
=
&
,
00
)( xtx
=
, (4.60)
где
)(t
ν
– центрированный белый шум с матрицей интенсивности
)(tV
,
а
0
x
– случайная векторная величина, независимая от
)(t
ν
, вектор сред-
них значений которой равен
0
x
, а матрица дисперсий равна
0
D
, т.е.
00
)}({ xtxM
=
, а
00000
}))()()({( DxtxxtxM
T
=−−
.
Будем предполагать, что собственные числа постоянной матрицы A
в (4.60) имеют отрицательные вещественные части. Тогда, в соответствии
с выражением (2.126) или П.5.10, справедливо равенство
0lim =
∞→
tA
t
e
, (4.61)
где
tA
e
– переходная матрица системы (4.60).
При этих условиях с помощью формулы Коши (2.132), приведённых
выше определений и первого равенства (4.58) можно найти [9], что век-
тор средних значений переменных состояния системы определяется вы-
ражением
0
)(
0
)(
xetx
ttA
−
=
, (4.62)
то есть монотонно затухает с ростом времени t.

185
Аналогично можно установить, что симметрическая квадратная
матрица дисперсий
)}()({)( txtxMtD
T
x
=
процесса
)(tx
удовлетворяет
дифференциальному матричному уравнению
TT
xxx
BtBVAtDtADttD )()()(),(
0
++=
,
000
),( DttD
x
=
(4.63)
и определяется выражением
∫
ττ+=
τ−τ−
−−
t
t
tAТtA
ttAttA
x
deBBVeeDettD
T
T
0
00
)()(
)(
0
)(
0
)(),(
. (4.64)
Если
constVtV
=
=
)(
, то при условии (4.61) существует предел
x
D
матрицы
),(
0
ttD
x
при
∞
→
t
. Этот предел определяется равенством
∫
∞
ττ
−∞→
∞→
τ==
0
0
),(lim
0
deBVBettDD
T
AТA
x
t
t
x
, (4.65)
причём матрица
x
D
удовлетворяет матричному алгебраическому урав-
нению Ляпунова вида
0=++
TT
xx
BVBADDA
. (4.66)
Таким образом, дисперсия вектора переменных состояния линейной
динамической системы с постоянными параметрами, на входе которой
действует случайный векторный процесс типа белого шума, является пе-
ременной величиной, т.е. зависит от времени. Если переходная матрица
tA
e
системы удовлетворяет условию (4.61), а входной белый шум явля-
ется стационарным, то дисперсия
),(
0
ttD
x
с ростом t стремится к неко-
торой постоянной матрице
x
D
. Причём эта матрица
x
D
– установивших-
ся дисперсий компонент вектора состояния может быть найдена либо с
помощью интеграла (4.65), либо из алгебраического уравнения (4.66).
С помощью выражений (4.58), (4.59) можно также установить, что
если Q и
1
Q
– постоянные симметрические неотрицательно определен-
ные матрицы, а в (4.60)
0)(
≡
ν
t
, то при всех
0
tt ≥
существует [9] сим-
метрическая матрица
)(tP
такая, что

186
0
00111
)()()()()(
1
0
xtPxtxQtxdQxxM
T
t
t
TT
=
+τττ
∫
. (4.67)
При этом указанная матрица
)(tP
определяется равенством
∫
τ+=
−τ−τ
−−
t
t
tAtA
ttAttA
dQeeeQetP
T
T
0
11
)()(
)(
1
)(
)(
(4.68)
и удовлетворяет дифференциальному матричному уравнению Риккати
QAtPtPAtP
T
++=− )()()(
&
,
10
ttt ≤≤
(4.69)
с конечным условием
11
)( QtP =
.
Аналогично, если в (4.60) матрица A такая, что выполняется условие
(4.61), то существует предел
∫
τ==
∞
ττ
∞→
0
)(lim dQeetPP
T
AA
t
, (4.70)
причём
P
– постоянная матрица, являющаяся решением матричного
уравнения Ляпунова
0=++
QAPPA
T
.
Отметим, что если матрица Q является положительно определённой,
т.е.
0
>
Q
, то при условии (4.61) решение уравнения Ляпунова – матрица
0
>
P
, т.е. также является положительно определённой.
Приведённые выражения (4.62) – (4.70) позволяют исследовать по-
ведение линейных многомерных систем под влиянием случайных воз-
действий в переходных режимах.
Приведём численный пример, ограничившись, для наглядности,
случаем одномерной динамической системы первого порядка [9] .
Пример 4.2. Рассмотрим систему, которая описывается дифферен-
циальным уравнением
)()()(
ttxtx
ν
+
α
−
=
&
, (4.71)
где коэффициент
0
>
α
;
00
)(
xtx
=
, причём
0
x
– случайная величина со
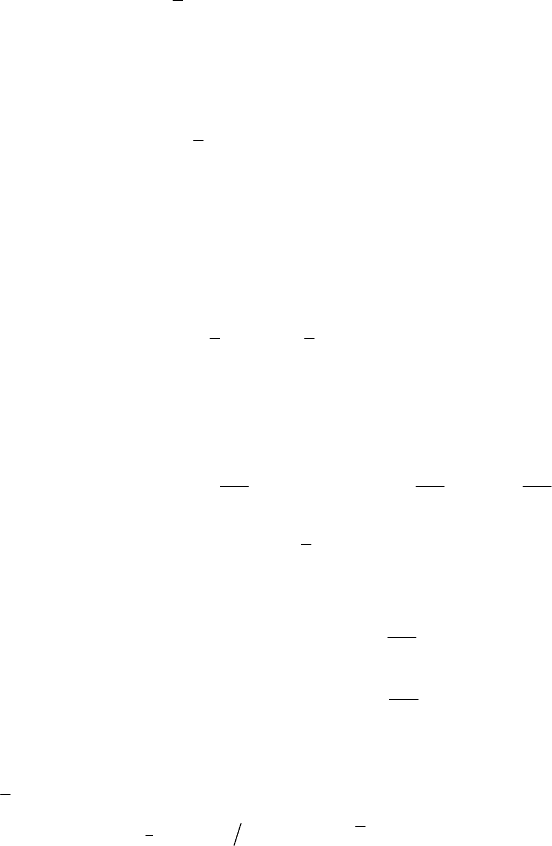
187
средним значением
0
x
и дисперсией
2
0000
}{ µ==
T
xxMD
;
)(t
ν
– некор-
релированный со случайной величиной
0
x
центрированный белый шум
интенсивности
2
σ
, т.е. случайное воздействие с нулевым средним и дис-
персией
2
)}()({ σ=νν ttM
T
.
Найти функции
)(tx
и
)(
tD
x
, описывающие изменения во вре-
мени среднего значения и дисперсии переменной состояния
)(
tx
ди-
намической системы (4.71).
Решение. В данном случае переходной матрицей системы является
экспонента
t
e
α−
. Поэтому, подставляя её в выражения (4.62), (4.64) и
полагая
0
0
=
t
,
α
−
=
A
,
1
=
B
и
2
)(
σ=tV
, найдём
0
)(
xetx
t
α−
=
, (4.72)
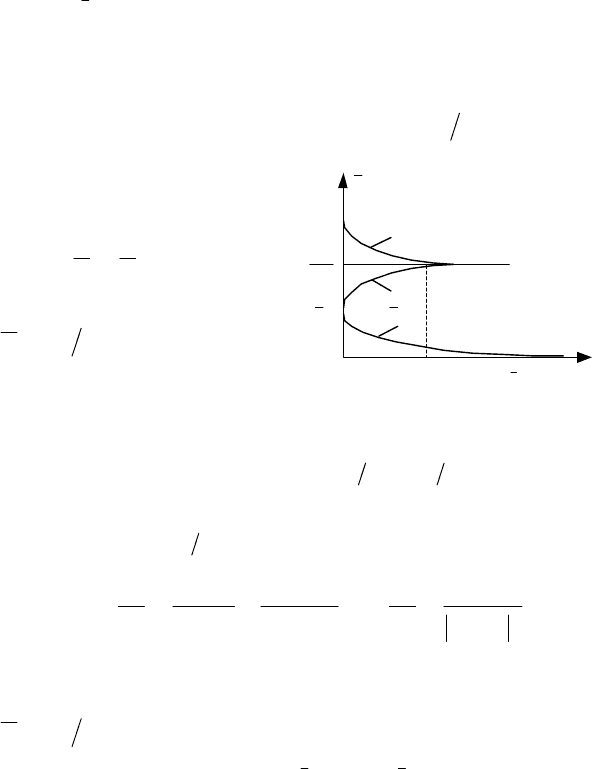
=
∫
τσ+µ=
τ−α−τ−α−α−α−
t
tttt
x
deeeetD
0
)(2)(2
0
)(
α
σ
+
α
σ
−µ=−
α
σ
+µ=
α−α−α−
22
)1(
2
2
2
2
2
0
2
2
22
0
ttt
eee
. (4.73)
Графики изменения величин
)(tx
и
)(tD
x
в соответствии с выра-
жениями (4.72) и (4.73) приведены на рис. 4.7. На этом рисунке:
кривая 1 – зависимость
)(tD
x
при
α
σ
>µ
2
2
2
0
,
кривая 2 – зависимость
)(tD
x
при
α
σ
<µ
2
2
2
0
.
Как видно из графиков, приведенных на рис. 4.7, при
0
>
α
, т.е. при
выполнении условия (4.61), среднее значение переменной состояния
)(tx
системы монотонно стремится к нулю. Практически можно считать,
что через время
α÷≈ )54(
x
t
величина
0)(
≈
tx
.
Дисперсия
)(tD
x
также изменяется с течением времени. Однако эта
функция стремится к некоторому не нулевому значению, которое опреде-
188
ляется дисперсией
2
σ
входного воздействия и параметром
α
динамиче-
ской системы.
Весьма существенно то, что время установления
dx
t
дисперсии
(длительность переходного процесса по дисперсии) примерно в два раза
меньше
x
t
– времени установления среднего значения переменной со-
стояния (см. рис. 4.7). Можно показать, что такое соотношение указан-
ных времён, при выполнении условия (4.61), справедливо при любом по-
рядке системы.
Из равенства (4.72) следует, что установившееся значение диспер-
сии переменной состояния системы (4.71) равно
ασ 2
2
.
Аналогичное выражение
можно получить и из соотноше-
ния (4.66), которое в рассматри-
ваемом случае имеет вид
0
2
=σ+α−α−
xx
DD
.
Отсюда также следует, что
ασ= 2
2
x
D
.
Это же выражение можно
получить и с помощью формулы
(4.57), если принять, что
x
y
=
.
Действительно, передаточ-
ная функция системы (4.71)
)(1)()()( α+=ν=
pppxpW
, а спектраль-
ная плотность входного воздействия
2
)( σ=ω
νν
S
. Следовательно, в дан-
ном случае
)(1)( α+ω=ω
jjW
, и по формуле (4.57) имеем
∫∫
∞
∞−
∞
∞−
ω
α+ω
σ
π
=ω
α+ω−
σ
α+ωπ
= d
j
d
jj
D
x
2
2
2
2
111
2
1
.
Сравнивая полученное выражение с равенством (4.12) и применяя
формулу Мак-Лена при
1
=
n
,
α=
0
c
,
1
1
=c
и
σ=
0
b
, снова получим
ασ= 2
2
x
D
.
Таким образом, уже при
2/
x
tt >
, где
x
t
– время затухания пере-
ходной матрицы
At
e
системы, статистические характеристики перемен-
Рис. 4.7
α
σ
2
2
0
x
)(tx
2
1
x
D
x
0
dx
t
x
t
t
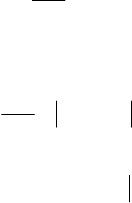
189
ных динамических систем с постоянными параметрами можно вычислять
по формулам, полученным для установившихся режимов.
§ 4.5. Вычисление дисперсии выходной переменной
Рассмотрим снова одномерную систему (рис. 4.6) в установившемся
режиме. Формально дисперсия
y
D
выходной переменной этой системы в
установившемся режиме может быть найдена из соотношения
)0(
yyy
RD =
, где
)(τ
yy
R
− автокорреляционная функция выходной пе-
ременной, определяемая формулой (4.44).
Однако этот путь очень сложен, поэтому для вычисления
)0(
yy
R
обычно используется формула обратного преобразования Фурье (4.9),
согласно которой
∫
ωω
π
=τ
∞
∞−
ωτ
.)(
2
1
)( deSR
j
yyyy
Полагая здесь
0
=
τ
и принимая во внимание формулу (4.47), получим
.)()(
2
1
2
∫
ωωω
π
=
∞
∞−
ϕϕ
dSjWD
y
(4.74)
Здесь
ω=
=ω
jp
pWjW )()(
.
Формула (4.74), очевидно, аналогична выражению (4.57), которое
определяет матрицу дисперсий выходной переменной многомерной сис-
темы также в установившемся режиме.
Так как
)(ω
ϕϕ
S
является четной функцией от частоты, а исследу-
ются, как правило, устойчивые системы, у которых
0)(Re <λ A
i
, то
для вычисления интеграла в (4.74) обычно используются приведенные в
параграфе 4.1 формулы Мак-Лена.
Эффективность влияния системы на проходящие через неё случай-
ные воздействия оценивают обычно путем сравнения дисперсии выход-
ной переменной с дисперсией входного воздействия. Поэтому формулы
(4.57) и (4.74) часто используются на практике при исследовании точно-
стных свойств динамических систем, работающих в условиях влияния
случайных воздействий.
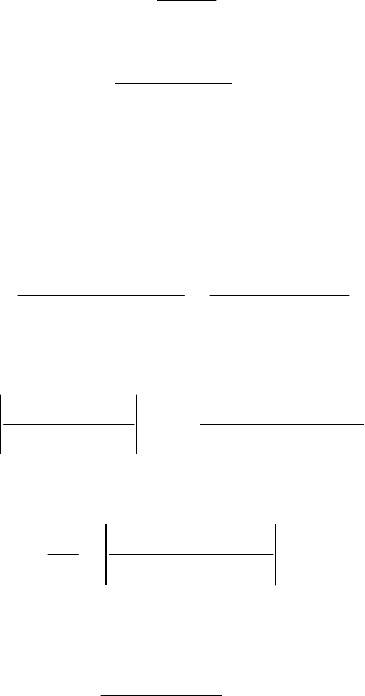
190
Пример 4.3. Рассматривая динамическую систему, показанную на
рис. 4.6, предположим, что на ее входе действует либо случайное воз-
действие
)(
1
tϕ
типа белого шума со спектральной плотностью
5,0)(
11
=ω
ϕϕ
S
,
либо цветной шум
)(
2
tϕ
со спектральной плотностью
2
4
2
)(
22
ω+
=ω
ϕϕ
S
.
Передаточная функция системы имеет вид
243
2
)(
2
++
=
pp
pW
.
Найти спектральную плотность и дисперсию выходной переменной
в обоих случаях. Сравнить дисперсии последней, учитывая, что в соот-
ветствии с таблицей 4.1, дисперсии воздействий
)(
1
tϕ
и
)(
2
tϕ
одинако-
вы и равны 0,5.
Решение. Запишем сначала комплексный коэффициент передачи за-
данной системы
ω+ω−
=
+ω+ω
=ω
432
2
24)(3
2
)(
22
jjj
jW
.
Далее, применяя формулу (4.47) при
)()(
1
tt ϕ=ϕ
, получаем выра-
жение, описывающее спектральную плотность выходной переменной,
222
2
2
16)32(
2
5,0
432
2
)(
11
ω+ω−
=
ω+ω−
=ω
j
S
yy
. (4.75)
Найдем теперь дисперсию выходной переменной при
)()(
1
tt ϕ=ϕ
.
По формуле (4.74) имеем
∫
ω
+ω+ω
π
=
∞
∞−
d
jj
D
y
2
2
24)(3
2
2
1
5,0
1
.
Так как степень полинома в знаменателе подынтегрального выраже-
ния равна двум, то для вычисления дисперсии воспользуемся приведен-
ной в параграфе 4.1 формулой Мак-Лена при
2
=
n
. Она имеет вид
210
2
2
00
2
1
2
2 ccc
cbcb
I
+
=
.
В нашем случае
2
0
=c
,
4
1
=c
,
3
2
=c
,
2
0
=b
,
0
1
=b
. Поэтому
