Гаспер Б.С., Липатов И.Н. ИВС и АСУТП. Учебное пособие
Подождите немного. Документ загружается.

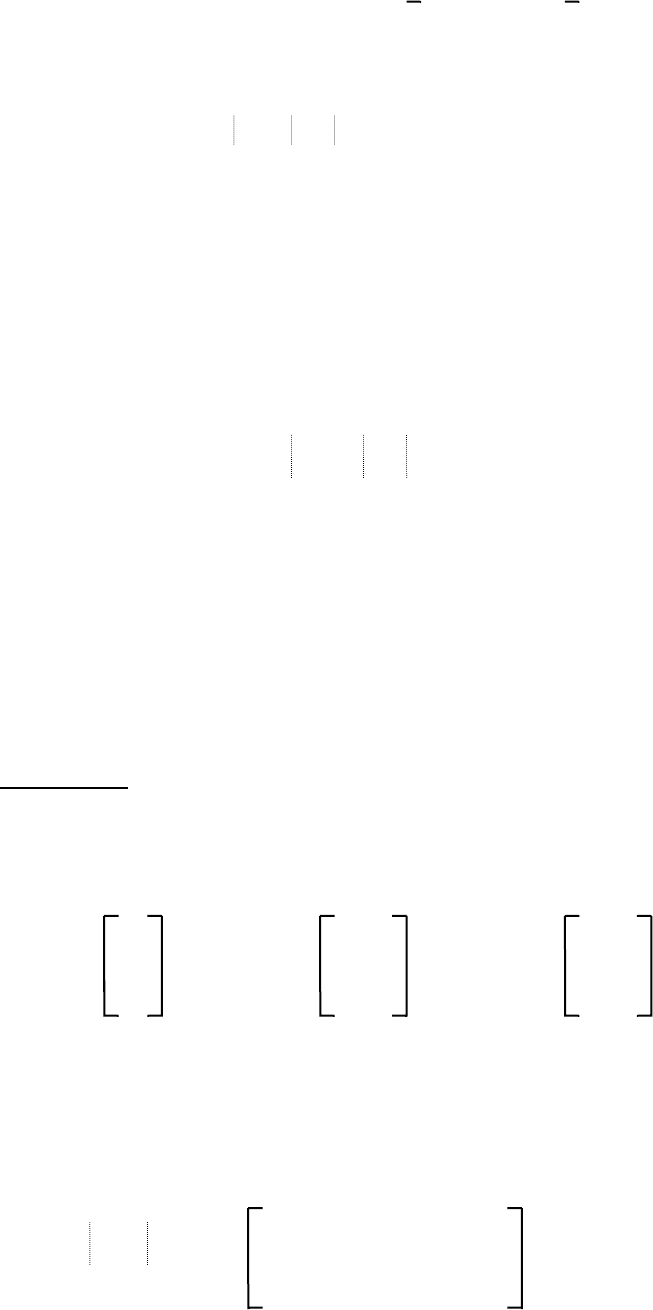
71
0 ⋅
c
n-1
(t - s)
n-1
u(s)
Поскольку управляемость означает, что управление
u влияет на все состояния x
посредством интегрального члена в (4.60), ясно, что система будет управляемой то-
гда и только тогда, когда подынтегральное выражение в (4.60) обеспечивает такое
влияние, т.е. когда ранг матрицы [
B AB ..... A
n-1
B] равен n. Условие управляемо-
сти не по состояниям, а по выходам можно получить, умножив обе части уравнения
(4.59) на
С:
y(t) = Cx = Ce
At
x
0
+
0
t
∫
[c
0
CB + c
1
(t-s)CAB + ... + c
n-1
(t - s)
n-1
CA
n-1
B]u(s) ds. (4.61)
Управляемость по выходам будет обеспечиваться в том случае, когда управление
u(t) будет влиять на все l выходов y(t), т.е. выход y будет полностью управляемым
тогда и только тогда, когда равен l ранг соответствующей матрицы управляемости
L
c
0
L
c
0
= [ CB CAB ..... CA
n-1
B]. (4.62)
Условие управляемости
для случая линейной нестационарной системы в
форме (4.24) с известными матричными функциями времени
A(t), B(t) состоит в
том, что (n
x n) - матрица M(t
0
,t
f
) невырожденная, т.е. det M(t
0
,t
f
) ≠ 0, где
t
f
M(t
0
,t
f
) =∫ Φ(t,t
0
)
-1
B(t)B
T
(t)[ Φ(t,t
0
)
T
]
-1
dt. (4.63)
t
0
здесь det
A - определитель матрицы А. Напомним, Φ(t,t
0
) - фундаментальная матри-
ца системы, т.е. решение уравнения (4.53).
Пример 4.2.
Система описывается уравнениями вида
&
(),
() () (),
xFxCut
zt Hxt t
=+
=+
⎫
⎬
⎭
υ
(4.64)
где
x
1
z
1
(t) υ
1
(t)
x = x
2
; z(t) = ; υ(t) = ;
x
3
z
2
(t) υ
2
(t)
F =
01 0
0
0
12
34
ff
ff
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
; C =
0
0
c
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
; H =
1
0
0
0
0
1
⎡
⎣
⎢
⎤
⎦
⎥
.
Проверим систему (4.64) на управляемость. Имеем
0 0 f
2
c
L
0
c
= [C FC F
2
C] = 0 f
2
c (f
1
f
2
+ f
3
f
4
)c .
c f
4
c (f
2
f
3 +
f
4
2
)c

72
Матрица
L
0
c
имеет ранг , равный трем, если f
2
c = 0. Следовательно, при f
c
с = 0 сис-
тема полностью управляема.
4.6.Нормализуемость для линейных систем
с сосредоточенными параметрами
Наиболее сильная форма управляемости называется нормализуемостью. Гово-
рят, что система является нормализуемой, если каждая координата вектора управ-
ления
u(t) в отдельности обеспечивает управляемость. Необходимое и достаточное
условие этого состоит в том, что матрица нормализуемости
Lc
i
не вырождена:
rank
Lc
i =
rank[b
i
Ab
i
...... A
n-1
b
i
] = n (4.65)
для всех i = 1,2,....,m, где
b
i
, i = 1,2,....,m - столбцы матрицы B. Заметим, что для
скалярных управлений u(t) управляемость и нормализуемость совпадают.
4.7. Автономное регулирование
При синтезе многомерных систем регулирования значительные затруднения
связаны с наличием статических и динамических перекрестных связей между раз-
личными входами и выходами системы. Если такие связи отсутствуют, а число
управляющих воздействий равно числу наблюдаемых координат, то матричная пе-
редаточная функция разомкнутой системы будет диагональной:
g
11
(s) 0
.
G(s) = C(sI - A)
-1
B = . . (4.66)
.
0 g
ll
(s)
Если диагональна также и матрица
G
с
(s) многомерного регулятора, то такой же (т.е.
диагональной) будет матричная передаточная функция замкнутой системы, связы-
вающая задание
y* с выходом y, при этом каждый отдельный контур регулирова-
ния может настраиваться независимо от остальных с использование обычных мето-
дов классической теории управления. К сожалению, для большинства многомерных
задач регулирования характерна многосвязность по входам и выходам.
Качество многомерных систем регулирования можно значительно повысить,
если применить различные методы компенсации (или развязывания) перекрестных
связей. Среди
большого числа способов компенсации перекрестных связей одним
из наиболее известных, классических, является метод синтеза автономной системы.
Рассмотрим понятие автономности на следующем примере. Пусть требуется управ-
лять выходами процесса
y(t) с помощью регулирующих воздействий u(t). Система
управления в состав в которой входит ряд отдельных контуров регулирования и
компенсатор перекрестных связей, показана на рис.4.8.
d
Возмущающие воздействия Gd
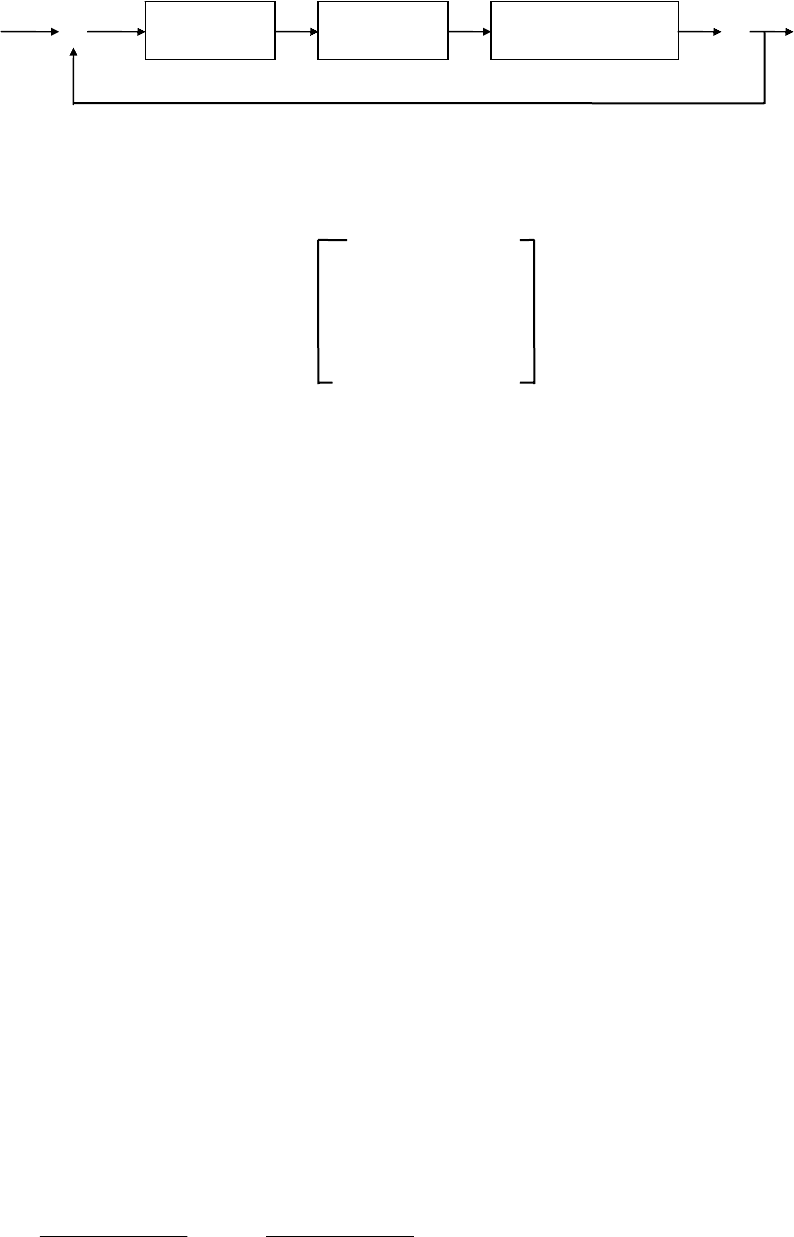
73
+ ε z u +
y* ⊗ Регулятор Gc Компенсатор G
1
Управляемый процесс G ⊗ y(t)
- +
Рис.4.8
Одномерные регуляторы определяют диагональную структуру передаточной мат-
рицы
Gc:
g
11c
0
.
Gc = . . (4.67)
.
0 g
llc
Передаточная матрица замкнутой системы с учетом передаточной матрицы
компенсатора
G
I
(Рис.4.8) будет задаваться выражением
y = (I + GG
I
G
c
)
-1
(GG
I
G
c
y* + G
d
d ) (4.68)
или
y = Ty* + T
d
d . (4.69)
Компенсатор
G
I
предназначен для ослабления влияния перекрестных связей. В иде-
альном случае он должен обеспечивать диагональность
T в каждый момент време-
ни.
T = (I + GG
I
G
c
)
-1
GG
I
G
c
(4.70)
или приближение
T к I при t
(
)
→
∞
→s 0 при некотором выборе настроек пара-
метров регуляторов. Очевидно, что автономность в этом смысле рассматривается
только для случая квадратных матриц
G, G
I
, Gc.
Поскольку матрица
G
c
диагональна, необходимым условием диагональности T
и предельного соотношения
T(0) → I при возрастании коэффициентов усиления
будет выполнение следующего соотношения:
GG
I
= diag G(s)
или
G
I
= G
-1
diag G(s), (4.71)
где diag
G - диагональная матрица, получаемая из G обнулением всех недиагональ-
ных элементов.
Если при этом компенсация будет полной, то передаточная матрица замкнутой
системы примет вид
y(s) = (I + GG
-1
diagGG
с
)
-1
(GG
-1
diagGG
c
y* + G
d
d),
или
∑
=
+
+
+
=
k
j
j
d
ij
iiii
i
iiii
iiii
i
sdsg
sgsg
sy
sgsg
sgsg
sy
cc
c
1
*
),()(
)()(1
1
)(
)()(1
)()(
)( i=1,2,...,l . (4.72)
Следует отметить, что в этом случае достигается полная автономность по за-
дающим воздействиям, и, несмотря на то, что каждое возмущение может влиять на
все выходы, эффект возмущения на любой из выходов может быть скомпенсирован
74
отдельным одномерным регулятором g
iic
(s).
Иногда бывают случаи, когда осуществить полную динамическую компенса-
цию слишком сложно или даже невозможно [см.4.71]. Напротив автономность в
статике всегда может быть обеспечена таким выбором компенсатора
G
Iss
, при кото-
ром
s→0
lim
T(s) - диагональная матрица (ss - индекс устанавливающегося состояния):
G
Iss
=
s→0
lim
G
I
(s) =
s→0
lim
(G
-1
(s)diagG(s)) = G
ss
-1
diagG
ss
.
(4.73)
Соответствующая передаточная матрица замкнутой системы определяется выраже-
нием
y = (I + GG
ss
-1
diagG
ss
G
c
)
-1
(GG
ss
-1
diagG
ss
G
c
y* + G
d
d).
(4.74)
При этом оказываются скомпенсированными все перекрестные связи в установив-
шемся состоянии, так что, изменяя коэффициенты усиления отдельных регулято-
ров, можно повысить качество системы. Однако даже в этой благоприятной ситуа-
ции в переходном процессе возможен период заметного влияния динамических свя-
зей, вследствие чего отдельные регуляторы могут действовать на объект в противо-
положных направлениях. По этой же причине, особенно если настройки регулято-
ров выбраны слишком жесткими, нежелательны большие значения интегральных
составляющих ПИД-законов.
Пример 4.3.
Рассмотрим дистилляционную колонну как систему, которой нуж-
но управлять. Имеем математическую модель колонны вида
y(s) = Gu(s),
G(s) =
07
19
20
18
23
110
,
,
,
+
+
+
s
s
s
0
04
16
23
18
,
,
+
+
s
s
0
0
21
17
,
+
s
. (4.75)
Система регулирования состоит из отдельных ПИ-регуляторов. Передаточная
матрица
G
с
(s) имеет вид
G
с
(s) =
gs
gs
gs
с
c
c
11
22
33
00
00
00
()
()
()
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
Рассмотрим для дистилляционной колонны задачу синтеза статической авто-
номной системы регулирования. Статическая задача решается выбором передаточ-
ной матрицы
G
Iss
в виде G
Iss
= G
ss
-1
diagG
ss
, где G(s) определяется соотношением
(4.75).
Имеем

75
G
ss
=
07 0 0
20 04 0
23 23 21
,
,,
,,,
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
; diag
G
ss
=
07 0 0
0040
0021
,
,
,
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, (4.76)
Откуда получаем
G
Iss
=
143 0 0
714 250 0
626 274 048
,
,,
,,,
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
07 0 0
0040
0021
,
,
,
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
100
714 1 0
626 274 1
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
,,
.
Автономная система регулирования, не учитывающая влияния возмущений,
показана на рис.4.9
y
1
* ε
1
z
1
+ u
1
y
1
⊗
g
c
11
g
I
1
⊗
Дистил-
y
2
* ε
2
z
2
+ u
2
y
2
⊗ g
c
22
g
I
2
⊗ ляционная
+
колонна
y
3
* ε
3
z
3
+
+ u
3
G(s) y
3
⊗
g
c
33
g
I
3
⊗
+ - +
Рис.4.9
Статическая автономность достигается за счет выбора коэффициентов усиления
компенсатора в виде
g
I
1
=
100
714
626
,
,
,
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
; g
I
2
=
0
10
274
,
,−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
;
g
I
3
=
0
0
10,
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
. (4.77)
Такие коэффициенты обеспечивают использование u
1
только для регулирования y
1
,
u
2
- для регулирования y
1
, y
2
и u
3
- для регулирования всех трех выходных перемен-
ных.
4.8. Модальное управление

76
Еще один подход к синтезу многомерных систем регулирования дает теория
модального управления. Эта теория существенным образом основывается на ли-
нейности рассматриваемых моделей; с ее помощью можно устанавливать желаемые
значения собственных чисел замкнутой системы. Разберем основные положения
модального управления на примере стандартной линейной системы в пространстве
состояний
&
х
= Ax + Bu + Гd, (4.78)
y = Cx. (4.79)
Будем предполагать, что в уравнениях (4.78), (4.79) размерности векторов
управления и выхода совпадают и равны размерности пространства состояний, что
A, B, C - постоянные матрицы и что все собственные числа матрицы А действи-
тельны и различны. Эти предположения не являются ограничивающими, они слу-
жат лишь для упрощения последующих выводов. Будем строить управление в виде
пропорциональной обратной связи по выходам
u(t) = -G
c
y = -G
c
Cx. (4.80)
Напомним теперь определение собственных чисел и собственных векторов. ес-
ли Λ
- диагональная матрица собственных чисел квадратной матрицы А:
λ
1
0
⋅
Λ = ⋅ , (4.81)
⋅
0 λn
то справедливы следующие соотношения:
RΛ = AR, (4.82)
ΛL = LA, (4.83)
где
R и L - матрицы нормированных собственных векторов (левых и правых) мат-
рицы
A, т.е. R и L определяются как решение векторных уравнений:
Ar
i
= λ
i
r
i
, i = 1,2,...,n, (4.84)
l
i
T
A = λ
i
l
i
, i = 1,2,...,n, (4.85)
а собственные числа λ
i
являются решениями характеристического уравнения
⎢
A -λ
i
I ⎜ = 0 , i = 1,2,...,n. (4.86)
Все векторы
l
i
и r
i
нормируются так, чтобы они были ортонормальны:
l
i
T
r
j
= δ
ij
, r
i
T
l
j
= δ
ij
, δ
ij
=
1
0
,
,
ij
ij
=
≠
⎧
⎨
⎩
(4.87)

77
или же в матричной форме:
LR = RL = I, (4.88)
где
R = [r
1
...... r
n
] , L = [l
1
...... l
n
]
T
. (4.89)
Умножая (4.82) слева на
L, а (4.83) - на R и используя (4.88), получим следующие
выражения:
Λ = LAR, (4.90)
RΛL = A. (4.91)
Подставляя (4.80) и (4.91) в (4.78), найдем
&
x
= (RΛL - BG
c
C)x. (4.92)
При получении соотношения (4.92) предполагалось, что
d = 0.
Если теперь взять матрицу
G
c
так, чтобы выполнялось равенство
G
c
= B
-1
RK, (4.93)
где диагональная матрица
K представляет собой матричный коэффициент усиле-
ния в цепи обратной связи
k
1
0
K = ⋅ , (4.94)
0 k
n
а матрицу наблюдения С равной L, то получим уравнение (4.92) в преобразованном
виде
&
x
= R(Λ - K)Lx. (4.95)
Сделав замену переменных
y = Lx, (4.96)
Получим уравнение относительно
y
&
y
= (Λ - K) y. (4.97)
Поскольку (Λ
- K) - диагональная матрица, система (4.97) разлагается на независи-
мые уравнения первого порядка, решениями которых являются функции

78
y
i
= α
i
e
(λi-ki) t
, i = 1,2,...,l. (4.98)
Возвращаясь к прежним переменным, получим решение в пространстве состояний
n
x =
∑
α
i
r
i
e
(λi-ki) t
. (4.99)
i=1
Здесь коэффициенты α
i
определяются начальными условиями. Изменяя k
i
, можно
как угодно менять собственные числа замкнутой системы, при этом между разными
выходами y
i
нет взаимосвязей, т.е. изменение коэффициента усиления k
i
влияет
только на i-моду. Это означает , что имеется возможность управлять модами замк-
нутой системы, причем перекрестные связи между координатами состояния не ска-
зываются на выходе. В качестве недостатков представленной методики следует от-
метить, что используются только пропорциональные регуляторы, матрица
С долж-
на совпадать с
L и, как показывает практика, трудна настройка системы. Блок-схема
системы приведена на рис.4.10.
y*=0 ε
Пропорциональный Модельный u Управляемый процесс x Измерительная y
⊗
регулятор К компенсатор B
-1
R
&
x
Ax
B
u
=
+
система С
+ -
y
Рис.4.10
Если размерность вектора управления m меньше размерности вектора состоя-
ния n, то модальное управление может быть применено к первым m собственным
векторам матрицы
A.
4.9. Аналитическое конструирование (синтез)
регуляторов непрерывных стационарных систем
Рассмотрим объект управления, возмущенное движение которого описывается
в первом приближении уравнением
&
x
= Ax + Bu; x(t
0
) = x
(0)
; t
0
= 0, (4.100)
где
A и B - заданные матрицы чисел размерности (n x n) и (n x m) соответственно.
Требуется найти матрицу чисел
C
T
размерности (m x n) уравнение регулятора
u = C
T
x (4.101)
такую, чтобы минимизировался функционал
79
J =
0
∞
∫
(x
T
Qx + U
T
u)dt, (4.102)
где Q - заданная положительно-определенная матрица размерности (n
x n)
(
x
T
Qx > 0 для всех х, это обозначается далее Q > 0).
Матрицу
C
T
закона управления (4.101) иногда называют матрицей коэффици-
ентов усиления регулятора.
Уравнения аналитического конструирования регуляторов имеют вид [11]
PA + A
T
P - PBB
T
P + Q = 0; (4.103)
C = -PB, (4.104)
где
P - симметричная матрица чисел размерности (n x n).
Матричное уравнение (4.103) имеет два названия: первое - матричное алгеб-
раическое уравнение Риккати, второе - уравнение Лурье.
Таким образом, процедура аналитического конструирования регуляторов
(процедура АКоР) состоит из трех операций: 1) решение системы нелинейных
алгебраических уравнений (4.103); 2) выделение из всего множества этих реше-
ний матрицы
P
0
> 0 ( нахождение P
0
осуществляется с использованием числен-
ного метода); 3) вычисление искомой матрицы коэффициентов усиления регуля-
тора по формуле
C = -P
0
B. (4.105)
4.10. Аналитическое конструирование регуляторов
непрерывных нестационарных систем
Рассмотрим полностью управляемый нестационарный объект, описываемый
уравнением
&
x
= A(t)x + B(t)u, x(t
0
) = x
(0)
, (4.106)
в которм
A(t) и B(t) известные на интервале [t
0
, t
1
] матрицы функций.
Пусть критерий качества имеет вид
J =
0
∞
∫
(x
T
Q(t)x + u
T
u)dt + x
T
(t
1
)P
(1)
x(t
1
), (4.107)
где
Q(t) и P
(1)
- заданные положительно-определенные матрицы функций и чисел
соответственно.
Требуется найти матрицу
C
T
(t) регулятора
u = C
T
(t)x, (4.108)
при которой минимизируется функционал (4.107).
В рассматриваемом случае уравнения аналитического конструирования регу-
ляторов имеют вид
C
(t) = -P(t)B(t); (4.109)
−
&
P
(t)=P(t)A(t) + A
T
(t)P(t) - P(t)B(t)B
T
(t) + Q(t); (4.110)
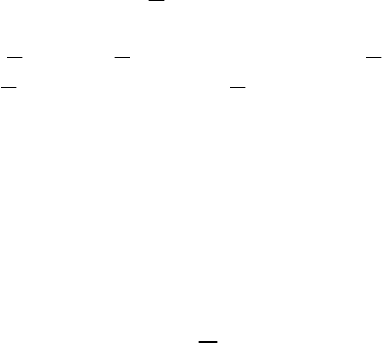
80
P(t
1
) = P
(1)
. (4.111)
Уравнение (4.110) называется матричным дифференциальным уравнением
Риккати.
Переходя к решению уравнения (4.110), введем «новое время» τ = t
1
- t и обо-
значим
P(t) = P(t
1
- τ) =
P
(τ). Тогда (4.110) и (4.111) примут вид
d
P
(τ)/dτ =
P
(τ) A(t
1
- τ) + A
T
(t
1
- τ)
P
(τ) -
P
(τ) B(t
1
- τ) B
T
(t
1
- τ)
P
(τ) + Q(t
1
- τ); (4.112)
P(0) = P
(1)
. (4.113)
Таким образом, краевая задача для уравнения (4.110) свелась путем ведения ново-
го (обратного) времени к задаче решения уравнения (4.112) с известным началь-
ным условием (4.113). Для его численного решения можно использовать любой
из известных методов интегрирования обыкновенных дифференциальных уравне-
ний (метод Рунге-Кутта, Эйлера и т.п.)
Решив уравнение (4.112), найдем искомую матрицу
C(t) = -
P
(t
1
- t)B(t).
4.11. Оптимальное управление при случайных внешних возмущениях
и измеряемом векторе состояний
Рассмотрим нестационарный объект управления
&
x
= A(t)x + B(t)u + ψ(t)f, x(t
0
) = x
(0)
, (4.114)
где
f(t)-k - мерный вектор внешних возмущений, являющийся гауссовским слу-
чайным процессом типа «белый шум». Здесь и далее будем полагать, что матема-
тическое ожидание
M{
f(t)} = 0. (4.115)
Корреляционная матрица этого процесса
R
f
(t’,t’’) = M{f(t’)f
T
(t’’)} = R
(1)
(t)δ(t’ - t’’), (4.116)
где R
(1)
(t) - положительно-определенная размерности (k x k), характеризующая
интенсивность «белого шума» в момент времени t’. Здесь
δ(t’ - t’’) =
∞=
≠
⎧
⎨
⎩
, ' '',
,'''.
tt
tt0
(4.117)
Пусть начальное состояние
x
(0)
также является гауссовским случайным векто-
ром, не зависящим от внешних возмущений и имеющим при M{
x
(0)
}=0 корреля-
ционную матрицу
M{
x
(0)
(x
(0)
)
T
}= R
(0)
. (4.118)
Рассмотрим критерий
