Гаспер Б.С., Липатов И.Н. ИВС и АСУТП. Учебное пособие
Подождите немного. Документ загружается.

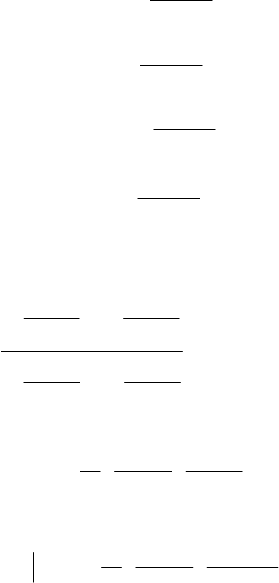
91
По результатам обработки реализаций случайных процессов X(t), Y(t) взаимная
корреляционная функция аппроксимирована следующими выражениями:
yx
t
KBe
tt() , ;=≥
−
β
0
yx
t
KBe
tt() , ,=≤
α
0
т.е. в соответствии с (5.12) имеем:
yx
yx
t
yx
t
K
KBe
KBe
t
tt
tt
()
() ,
() ,
=
=≥
=≤
⎧
⎨
⎪
⎩
⎪
+−
−
β
α
0
0
. (5.17)
Используя формулу (5.14), получим
x
t
x
t
yx
t
x
t
KAe
KAe
KBe
KBe
SL
A
S
SL
A
S
SL
B
S
SL
B
S
+−
−
+−
−
==
+
==
−
==
+
==
−
⎫
⎬
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
() { } ;
() { } ;
() { } ;
() { } .
α
α
β
α
α
α
β
α
(5.18)
Согласно (5.13), с учетом (5.18) находим:
WS
B
S
B
S
A
S
A
S
() ,=
+
−
−
+
−
−
11
11
βα
α
α
откуда передаточная функция динамического объекта
WS
B
A
S
S
()=⋅
+
⋅
+
+
α
β
α
α
β
2
. (5.19)
Определим W(j
ω
). Имеем
Wj WS
B
A
j
j
Sj
() ()
ω
α
β
α
ω
α
ωβ
ω
==⋅
+
⋅
+
+
=
2
.
Определим W(P). Получим
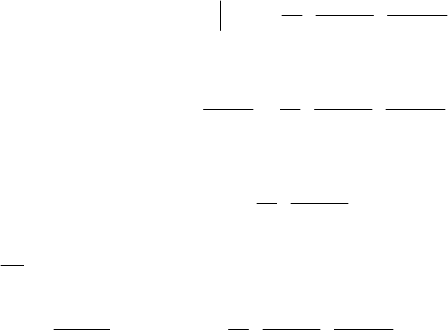
92
WP WS
B
A
P
P
SP
() ()==⋅
+
⋅
+
+
=
α
β
α
α
β
2
.
Из (5.6) имеем
WP
Yt
Xt
B
A
P
P
()
()
()
==⋅
+
⋅
+
+
α
β
α
α
β
2
или
()() ()()PYt
B
A
PXt+=⋅
+
+
β
α
β
α
α
2
.
Так как
P
d
dt
≡ , то окончательно получим
dY t
dt
Yt
B
A
dX t
dt
Xt
()
()
()
()+⋅ = ⋅
+
+⋅
⎡
⎣
⎢
⎤
⎦
⎥
β
αβ
α
α
2
(5.20)
Соотношение (5.20) есть искомое дифференциальное уравнение, описывающее
динамический объект.
93
5.3. Статистическая идентификация динамического объекта
во временной области
Современное состояние теории и практики идентификации характеризуется
интенсивной разработкой статистических методов идентификации, ориентирован-
ных на применение ЭВМ. К этим методам относится и метод минимума статисти-
ческой неопределенности, рассматриваемый в данном разделе. Он является непа-
раметрическим временным методом идентификации динамического объекта.
5.3.1.Постановка задачи статистической идентификации динамического объ-
екта во временной области
Рассмотрим одномерный динамический объект в условиях нормального
функционирования. Функция x(t), описывающая воздействие на объект, и функция
y(t), описывающая реакцию объекта на это воздействие, определены на некотором
множестве моментов времени T, зависящем от характера эксперимента. В общем
случае x(t) и y(t)являются реализациями случайных процессов на входе и выходе
объекта. Будем
называть функции x(t) и y(t) входным и выходным сигналами объ-
екта. Тогда задачу статистической идентификации можно сформулировать сле-
дующим образом.
В процессе нормального функционирования одномерного объекта син-
хронно (непрерывно или дискретно) измеряются входной x(t) и выходной y(t) сиг-
налы. По результатам измерения необходимо определить хотя бы приближенное
значение оператора, ставящего в
однозначное соответствие входной и выходной
сигналы, т.е. нужно получить математическую модель объекта.
Если моделью объекта (системы) является зависящий от времени оператор
A(t) такой, что
y(t) = A(t)⋅x(t),
то задачей статистической идентификации будет определение оценки этого опера-
тора A
0
(t), позволяющей получать оценку
y
0
(t) = A
0
(t)
⋅
x(t).
В другой формулировке задачей статистической идентификации является
нахождение оценки A
0
(t) истинного оператора системы A(t) по реализациям слу-
чайных процессов x(t) и y(t).
Соответствие между моделью и оригиналом может быть достигнуто лишь в
случае близости в некотором смысле оценки A
0
(t) к истинному значению A(t). При
этом будет соблюдаться требование близости y
0
(t) к y(t).
Для оценки качества идентификации вводят функцию потерь
ρ
[y(t), y
0
(t)],
на математическое ожидание которой накладывается требование
M{
ρ
[y(t), y
0
(t)] } = min.
Выбором вида функции потерь определяется критерий близости выходных
сигналов модели и оригинала. Наиболее часто применяют квадратичную функцию
потерь вида
ρ
[y(t), y
0
(t)] = [y(t) - y
0
(t)]
2
.
Получим основное уравнение статистической идентификации, которому
должна удовлетворять оптимальная оценка оператора A
0
(t). Примем следующие
допущения: объект линеен, наблюдаемые случайные процессы стационарны (в
широком смысле) и стационарно связаны.
С учетом принятых допущений выходной сигнал объекта, функционирую-
94
щего неограниченно долго, имеет вид
yt xt d nt() ( ) ( ) ()=−+
∞
∫
ωτ τ τ
0
, (5.21)
где
ω(τ)
- импульсная переходная функция (ИПФ) линейной системы;
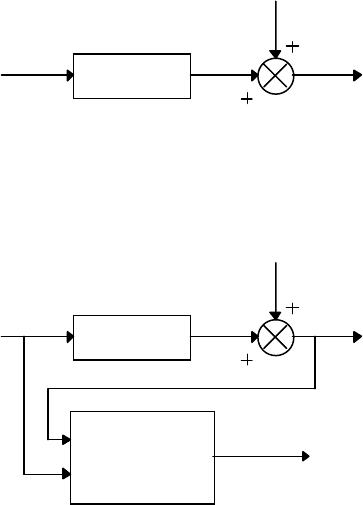
n(t) - случайная помеха (рис. 5.2).
ω
(t)
x
(t)
z
(t)
y
(t)
n(t)
Рис. 5.2.
Задача статистической идентификации динамического объекта заключается
в определении оценки
)
ω
()t ИПФ
ω(
t
)
по результатам наблюдений за сигналами
x(t) и y(t) (рис.5.3).
ω
(t)
x
(t)
z
(t)
y
(t)
n(t)
Получение
оценки ИПФ
ω(
t
)
)
ω
()t
Рис. 5.3.
Определение искомой ИПФ из уравнения (5.21) сопряжено со значитель-
ными погрешностями вследствие неточности регистрируемых сигналов, обуслов-
ленной помехами и измерительными ошибками, сложностью аппроксимации сиг-
налов аналитическими выражениями.
Для повышения качества восстановления ИПФ необходима предваритель-
ная обработка сигналов. Аналитически это условие означает следующее. Пусть
случайные сигналы на входе объекта идентификации
центрированы, тогда, умно-
жая левую и правую части уравнения (5.21) на
x(t-
θ
) и осредняя результат, полу-
чаем
Mxt yt M xt xt d Mxt nt[( )()] [ ()( )( ) ] [( )()]−= −−+−
∞
∫
θωτθττθ
0
,
где М - оператор математического ожидания; n(t) - приведенная к выходу помеха,
некоррелированная со входным сигналом.
Учитывая коммутативность операции определения математического ожи-
дания и интегрирования, получаем
Mxt yt Mxt xt d[( )()] () [( )( )]−=⋅−−
∞
∫
θωτ θττ
0
или
RRd
xy xx
() () ( )
θωτθττ
=−
∞
∫
0
. (5.22)
95
Уравнение (5.22) представляет собой запись известного уравнения Винера-
Хопфа и связывает искомую ИПФ с корреляционной функцией входного сигнала
R
xx
(
τ
) и взаимной корреляционной функцией входного и выходного сигналов
R
xy
(
θ
) идентифицируемого объекта.
ИПФ, определяемая из уравнения Винера-Хопфа, оптимальна по критерию
минимума среднеквадратичной ошибки
M{ [y(t) - y
0
(t)]
2
} = min.
При реализации случайных сигналов они регистрируются на конечных ин-
тервалах наблюдения
T
н
, а линейная система с бесконечной памятью аппроксими-
руется системой с конечной памятью, поэтому бесконечный верхний предел в
уравнении (5.22), исходя из физических соображений заменяют на конечный
Τ
ω
,
такой, что для всех
τ > Τ
ω
,
ω(τ)
≈ 0. Это утверждение справедливо для физически
реализуемых систем, у которых
ωτ θ τ τ ε
ω
() ( )Rd
xx
T
−<
∞
∫
при
τ > Τ
ω
.
С учетом сказанного, основное уравнение статистической идентификации
принимает вид
RRd
xy xx
T
() () ( )
θωτθττ
ω
=−
∫
0
. (5.23)
При непараметрической идентификации динамических объектов решение
уравнения Винера-Хопфа получают в виде последовательности значений ИПФ.
Наиболее часто применяют численные методы решения уравнения (5.23) во вре-
менной и частотной областях.
5.3.2.Некорректность задачи статистической идентификации
динамического объекта
Представим уравнение (5.23) в операторном виде:
A
ω
= R
xy
, (5.24)
где
ω
- искомая функция из некоторого нормированного пространства W; R
xy
- за-
данная функция из нормированного пространства
R; A - заданный линейный инте-
гральный оператор перехода из
W в R.
Согласно классическому определению задача статистической идентифика-
ции - задача решения уравнения (5.24) - называется корректно поставленной, по
Адамару:
•
если для любого элемента R
xy
∈
R существует решение
ω
из пространства W;
•
решение единственно в W;
•
решение устойчиво на пространствах R и W, т.е. для любого
ε
> 0 можно ука-
зать такое
δ(ε)
, что из неравенства
ρ
R
(R
xy1
, R
xy2
)
≤
δ(ε)
следует
ρ
W
(
ω
1
,
ω
2
)
≤
ε
,
причем
A
ω
1
= R
xy1
, A
ω
2
= R
xy2
.
В случае невыполнения указанных требований задача оказывается некор-
ректно поставленной.
В практических задачах идентификации реальных объектов существование
решений и принадлежность их определенным множествам вытекают из физиче-
ского смысла их постановки. Тем самым первые два требования корректности вы-
полняются естественным образом.

96
Задача статистической идентификации некорректна вследствие невыполне-
ния условия устойчивости. Покажем причины неустойчивости при нахождении
ИПФ идентифицируемого объекта традиционными способами.
При численном решении во временной области интегральное уравнение
Винера-Хопфа аппроксимируется системой линейных алгебраических уравнений
(СЛАУ).
Rt c tRt t t
xy i j j xx i j
j
n
() ( ) ( ) ,=−
=
∑
ω
Δ
0
in= 0, (5.25)
где
t
i
= i
Δ
t; t
j
= j
Δ
t;
Δ
t = T
ω
/n - шаг дискретности по времени; c
j
- коэффициент, за-
висящий от выбора квадратурной формулы, аппроксимирующей интеграл.
Решение системы (5.25) дает
n+1 дискретное значение ИПФ объекта. В
матричной форме СЛАУ (5.25) имеет вид
R
xy
= R
xx
⋅
W (5.26)
где
R
xy
матрица-столбец свободных членов, элементы которой - ординаты взаим-
ной корреляционной функции
R
t
Rti n
ixyi
==
1
0
Δ
(), ,; R
xx
- квадратная матрица ко-
эффициентов СЛАУ (5.25), имеющая в случае квадратурной формулы прямо-
угольников симметричную относительно главной диагонали форму:
R
R
Rt
Rt
Rt
xx
xx
xx
xx i
xx n
=
()
()
()
()
0
1
K
K
Rt
R
Rt
Rt
xx
xx
xx i
xx n
()
()
()
()
1
1
1
0
K
K
−
−
K
K
K
K
K
K
Rt
Rt
Rt
Rt
xx j
xx j
xx j i
xx n j
()
()
()
()
−
−
−
1
Rt
Rt
Rt
R
xx n
xx n
xx n i
xx
()
()
()
()
−
−
1
0
K
K
. (5.27)
Матрица-столбец
W=[
ω
i
] состоит из элементов, которые представляют со-
бой ординаты искомой ИПФ.
Особенностью получаемой СЛАУ является составление ее элементов по
результатам предварительной обработки реализации входного и выходного сигна-
лов объекта, при этом неизбежны измерительные и вычислительные погрешности.
При решении СЛАУ существует несколько источников погрешностей. Один из
таких источников характерен для решения практических
задач в случае, когда
элементы матрицы коэффициентов алгебраической системы известны лишь при-
ближенно. Неточность исходных данных порождает ошибки в решении, так как
изменение коэффициентов системы уравнений в пределах заданной точности вле-
чет за собой изменение решения.
Теоретически решение СЛАУ (5.25) определяется формулой
WR R
xx xy
=⋅
−1
,
причем обратная матрица
R
xx
−1
существует лишь при отличном от нуля определите-
ле
R
xx
. Изменение элементов матрицы R
xx
в пределах точности их задания может
привести к матрице с нулевым определителем или даже может изменить его знак.
В результате исходная СЛАУ практически оказывается несовместной. Таким об-
разом приближенное задание корреляционных функций предопределяет плохую
обусловленность обратной матрицы
R
xx
−1
, что приводит к нарушению условия ус-
тойчивости.
К факторам, влияющим на точность задания исходных данных и искажаю-

97
щих результаты решения интегрального уравнения Винера-Хопфа относятся:
относительно невысокая точность оценок корреляционных функций, обусловлен-
ная в основном недостаточной длиной зафиксированных реализаций случайных
процессов; погрешность численных расчетов, связанная с заменой бесконечного
верхнего предела в уравнении (5.22) конечным
T
ω
, самого интеграла - квадратур-
ной формулой.
Таким образом, вследствие невыполнения условия устойчивости, задача
статистической идентификации некорректна. Устойчивое решение может быть
получено при использовании регуляризирующих алгоритмов статистической
идентификации.
5.3.3.Метод минимума статистической неопределенности
Рассмотрим для решения задачи статистической идентификации метод ми-
нимума статистической неопределенности. Этот метод идентификации основан на
решении интегрального уравнения [13]
RRd
xy xx
T
() () (,)
τωθτθθ
=
∫
0
, (5.28)
в котором
T - время затухания ИПФ; корреляционная функция R
xx
(
τ, θ
) определя-
ется соотношением [13]
R
T
xt xt dt T
xx
Н
T
Н
(,) ( )( ) ,, [, ]
τθ τ θ τθ
=−−∈
∫
1
0
0
, (5.29)
где
T
н
- интервал наблюдения реализации процесса x(t).
Уравнение (5.28) справедливо лишь при стационарных входных сигналах.
Аналогично уравнению Винера-Хопфа, уравнение (5.28) также может быть
представлено в дискретном виде системой линейных алгебраических уравнений:
Rit t jtRitjti N
xy
j
N
xx
() ( ) (, ), ,,,ΔΔ Δ ΔΔ==−
=
−
∑
ω
0
1
01 1K , (5.30)
где
N - число точек ИПФ;
Δ
t - интервал дискретизации; R
xy
и R
xx
при замене их ар-
гументов
i
Δ
t и j
Δ
t целочисленными сдвигами определяются уравнениями
Ri
LN
yx
xy k k i
kN
L
()=
−
−
=
−
∑
1
1
, i
N
=
−
01 1,, ,K ; (5.31)
Rij
LN
xx
xx k i k j
kN
L
(, )=
−
−−
=
−
∑
1
1
, i
j
N
,,,,
=
−
01 1K . (5.32)
Здесь
y
k
= y(t
k
); t
k
= k
Δ
t; L-N - число точек осреднения характеристик; x
k-i
= x(t
k-i
);
t
k-i
= (k - i)
Δ
t; N-1 - максимальный временной сдвиг.
В матричной форме уравнение (5.30) имеет следующий вид
R
xy
= R
xx
⋅
W, (5.33)
где
R
xx
- симметричная матрица размера NxN:

98
R
R
R
R
RN
xx
xx
xx
xx
xx
=
−
(,)
(,)
(,)
(, )
00
01
02
01
K
R
R
R
RN
xx
xx
xx
xx
(,)
(,)
(,)
(, )
01
11
12
11
K
−
R
R
R
RN
xx
xx
xx
xx
(,)
(, )
(,)
(, )
02
12
22
21
K
−
K
K
K
K
K
RN
RN
RN
RN N
xx
xx
xx
xx
(, )
(, )
(, )
(,)
01
11
21
11
−
−
−
−−
K
; (5.34)
R
xy
и W - матрицы-векторы. Причем
R
xy
= [R
xy
(0) R
xy
(1) .... R
xy
(N-1)]
T
; (5.35)
W = [W(0) W(1) .... W(N-1)]
T
. (5.36)
Точность идентификации, осуществляемой по уравнению (5.28), достаточ-
но велика.
5.3.4.Оценка точности статистической идентификации
динамического объекта
Оценим точность статистической идентификации динамического объекта
путем определения относительной среднеквадратичной погрешности идентифика-
ции по формуле:
σ
ωω
ω
W
ii
i
N
i
i
N
=
−
=
−
=
−
∑
∑
()
)
2
0
1
2
0
1
, (5.37)
где
ω
i
и
)
ω
i
- значения истинной и восстановленной ИПФ; N - количество вычис-
ленных значений ИПФ.
Введем обозначение
zt xt d() ( ) ( )=−
∞
∫
ωτ τ τ
0
. (5.38)
Тогда соотношение (5.21) примет вид
y(t) = z(t) + n(t). (5.39)
Обозначим через
σ
z
2
дисперсию сигнала z(t) на выходе динамического объекта, а
через
σ
n
2
- дисперсию случайной помехи n(t). Эти дисперсии могут быть определе-
ны по формулам
σ
zi
i
L
L
zz
22
1
1
=−
=
∑
(), (5.40)
σ
ni
i
L
L
nn
22
1
1
=−
=
∑
(), (5.41)
где
z
L
z
i
i
L
=
=
∑
1
1
; n
L
n
i
i
L
=
=
∑
1
1
.
Введем обозначение
S
y
n
z
=
σ
σ
, (5.42)
где S
y
- отношение шум - выходной сигнал, которое задается как отношение сред-
99
неквадратических значений шума и выходного сигнала.
Среднеквадратическая погрешность идентификации
σ
ω
динамического
объекта зависит от величины S
y
, т.е. имеет место функциональная зависимость ви-
да
σ
ω
= f
1
(S
y
). (5.43)
Кроме того
σ
ω
, зависит от величины L:
σ
ω
= f
2
(L). (5.43)
Величина
σ
ω
возрастает с увеличением S
y
.
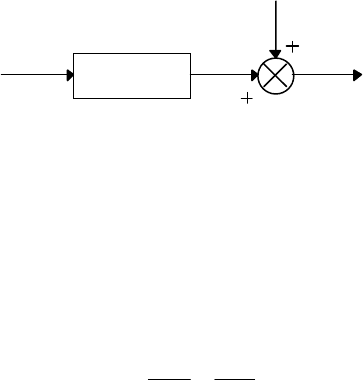
5.4. Идентификация путем анализа импульсной реакции (весовой функции)
Рассмотрим систему, описываемую соотношением вида (рис.5.4)
yt g kut k vt
k
() ( ) ( ) ()=−+
=
∞
∑
0
1
, (5.45)
где u(t) - скалярный входной сигнал; y(t) - скалярный выходной сигнал; g
0
(k) - ис-
тинная импульсная реакция или весовая функция, которая полностью определяет
поведение системы; t = 0,1,2,... - дискретные моменты времени; v(t) - помеха в мо-
мент времени t.
ОУ (ТП)
u(t)
y
(t)
v(t)
Рис. 5.4.
Если к системе, описываемой соотношением (5.45), приложить импульсное
воздействие
ut()
,
,
=
⎧
⎨
⎩
α
0
,0
,0
≠
=
t
t
(5.46)
то выходной сигнал y(t) будет равен
y(t) =
α
⋅
g
0
(t)+ v(t). (5.47)
Из (5.47) имеем
)
gt
yt vt
()
() ()
=−
αα
, (5.48)
где
)
gt()- оценка весовой функции g
0
(t); v(t)/
α
- ошибка определения g
0
(t).Чтобы
уменьшить v(t)/
α
, необходимо увеличить
α
.
При идентификации по импульсному воздействию часто возникают техни-
ческие трудности, связанные с формированием и использованием импульсных
входных сигналов. Этот метод нельзя применить к линеаризованным системам,
так как амплитуда импульса по определению не может быть малой. Другими сло-
вами, при таком входном сигнале система может проявить нелинейные эффекты,
нарушающие линеаризованное поведение
, положенное в основу модели системы.
Этот метод предполагает идентификацию вне процесса управления.
5.5. Идентификация путем определения реакции на ступенчатое
воздействие

100
Приложим к системе, описываемой соотношением (5.45), ступенчатое входное
воздействие
ut()
,
,
=
⎧
⎨
⎩
α
0
t
t
≥
<
0
0
,
.
(5.49)
Тогда выходной сигнал y(t) будет равен
yt g k vt
k
t
() ( ) ()=⋅ +
=
∑
α
0
1
. (5.50)
Из (5.50) имеем
yt g k vt
k
t
() ()()−= ⋅ + −
=
−
∑
11
0
1
1
α
. (5.51)
Из (5.50), (5.51) получим
y(t) - y(t-1)=
α
⋅
g
0
(t)+ v(t) - v(t-1). (5.52)
Из (5.52) имеем
)
gt
yt yt vt vt
()
() ( ) () ( )
=
−
−
−
−
−
11
αα
, (5.53)
где
)
gt()- оценка весовой функции g
0
(t); [v(t) - v(t-1)]/
α
- ошибка определения g
0
(t).
Если определение коэффициентов весовой функции действительно является це-
лью, использование (5.53) может сопровождаться значительными ошибками в
большинстве практических приложений.
Ступенчатый входной сигнал является наиболее простым для применения
(он соответствует, например, открыванию или закрыванию входного клапана либо
включению или выключению входного напряжения).
5.6. Эмпирическая оценка передаточной функции ОУ(ТП)
Введем следующую оценку передаточной функции ОУ(ТП)
$
$
()
()
()
G
Y
U
N
i
N
N
l
ω
ω
ω
=
, (5.54)
где
Y
N
yt
N
it
t
N
() ()
ω
ω
=
−
=
∑
1
1
l , (5.55)
U
N
ut
N
it
t
N
() ()
ω
ω
=
−
=
∑
1
1
l , (5.56)
ω
π
=
2 k
N
, (k = 0,1,...,N-1). (5.57)
Здесь
$
$
()G
N
i
l
ω
- эмпирическая оценка передаточной функции ОУ(ТП); U
N
(
ω
) -
дискретное преобразование Фурье (ДПФ) последовательности u(1), u(2),...,u(N);
Y
N
(
ω
) - ДПФ последовательности y(1), y(2),...,y(N); G
N
i
()l
ω
- истинная передаточ-
ная функция ОУ(ТП) в точке z
i
= l
ω
, -
π
≤
ω
≤
π
; t = 1, 2, .. - дискретные моменты
времени.
