Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2
Подождите немного. Документ загружается.

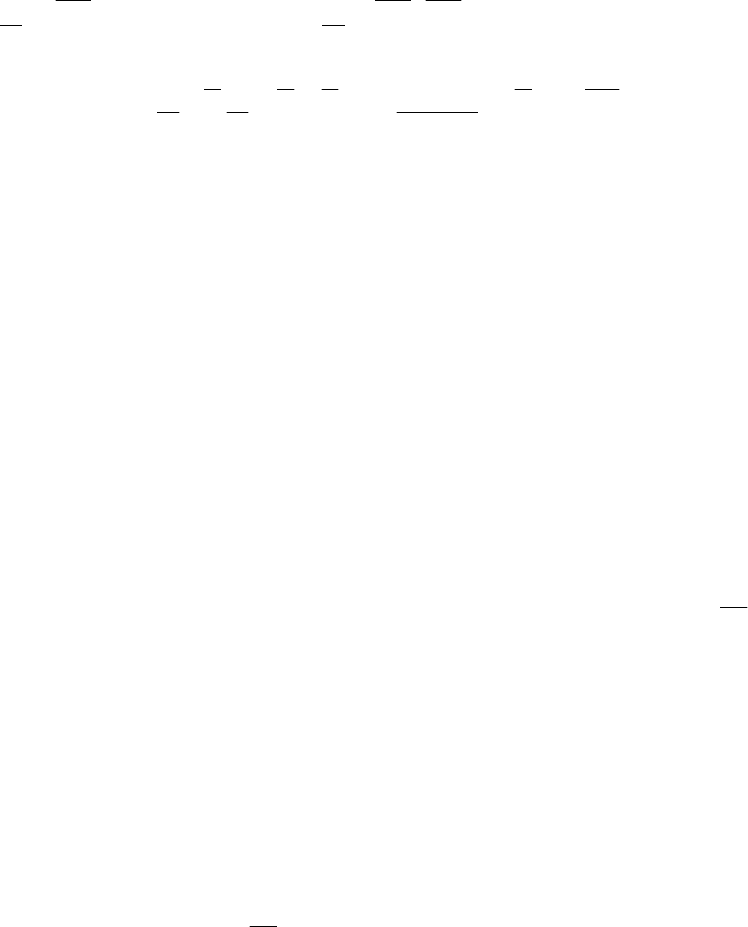
41
Тогда после подстановки в формулу Дюамеля (10.33а) этих вели-
чин вместе с найденной в примере 10.11 переходной проводимостью
RC
t
e
R
ty
1
)(
, а также
1
()
t
R
CRC
yt e e
R
получим:
0
1
() [ ].
t
tt
t
RC
TTT T
ECE
it e e e d e e
TR TRC
10.4.3. Понятие об импульсных функциях
Если в примере 10.11 уменьшать сопротивление R, то начальное
значение тока, очевидно, будет возрастать с одновременным уменьше-
нием постоянной времени
.RC
При теоретическом рассмотрении
случая
0R
получим бесконечно большой импульс тока нулевой дли-
тельности. Для математического описания подобных зависимостей ис-
пользуется так называемая функция Дирака (δ-функция или единичный
импульс), описание которой укладывается в две формулы:
() 1, () 0 при 0.tdt t t
(10.34)
Из этого определения δ(t) следует связь ее с единичной функцией
Хевисайда:
() 1(),
t
tdt t
откуда получается и формула () 1().
d
tt
dt
Тогда в нашем гипотетическом случае подключения идеального кон-
денсатора С к источнику постоянной ЭДС Е напряжение на конденсато-
ре и ток через него можно описать выражениями:
() 1(), () ().
C
ut E t it CE t
Реакцию некоторой цепи на импульсное воздействие
)()(
t
V
t
v
можно определить как
() (), где ()
f
t V kt kt
импульсная характе-
ристика этой цепи. Очевидна и связь импульсной характеристики с пе-
реходной функцией:
() ().
d
kt ht
dt
10.4.4. Сведение расчета переходного процесса
к нулевым начальным условиям
Обратим внимание, что все выкладки и расчеты, описанные в раз-
делах 10.4.1 и 10.4.2, сделаны в предположении, что независимые
начальные условия – нулевые. Если же это условие не выполняется, то,
прежде чем использовать формулы Дюамеля, нужно привести расчет
переходного процесса к нулевым начальным условиям.
42
Докажем возможность выполнения этого расчетного приема как
при замыкании, так и при размыкании рубильника в одной из ветвей
сложной цепи с ненулевыми независимыми начальными условиями.
10.4.4.1. Замыкание рубильника (рис. 10.26, а)
Включим в ветвь с рубильником два одинаковых источника
ЭДС e(t) противоположной полярности. Токи в ветвях послекоммутаци-
онной цепи не изменятся при любых значениях ЭДС, так как источники
компенсируют действие друг друга.
Теперь применим метод наложения, оставив в одной из подсхем
все источники активного четырехполюсника и нижнюю ЭДС e(t), а
во
второй – только верхнюю ЭДС e(t) (рис. 10.26, б). Тогда ток в любой
ветви, например, ab или cd можно представить в виде суммы двух со-
ставляющих:
() () (), () () ().
ab ab ab cd cd cd
ititit ititit
Подберем величину ЭДС такой, чтобы в первой подсхеме и после
замыкания рубильника ток через него не протекал, т. е.
0.
cd
i
А зна-
чит, величина ЭДС должна быть такой, каким было напряжение на за-
жимах ветви cd до коммутации:
до до
p
() () ().
cd
ututet
Тогда в этой под-
схеме будет сохраняться установившийся докоммутационный режим.
В частности, в ветви ab будет по-прежнему протекать ток
до
() ().
ab
ab
itit
Во второй подсхеме действует единственная ЭДС
до
p
() (),et u t
ко-
торая направлена по току рубильника в послекоммутационной цепи,
причем до коммутации ни токов, ни напряжений в цепи не было. По-
этому токи
пн пн
() () и () () ()
ab ab cd cd cd
itit ititit
будут определяться
43
при нулевых независимых начальных условиях. В верхнем индексе
«пн» используются первые буквы слов в выражении «
переходный про-
цесс в цепи с
нулевыми начальными условиями».
Таким образом, чтобы свести расчет переходного процесса к нуле-
вым начальным условиям, нужно пройти два этапа. Сначала следует
рассчитать установившийся режим докоммутационной цепи, определив
не только мгновенное значение тока в интересующей нас ветви, но и
напряжение на зажимах рубильника
до
р
().ut
А затем выполнить расчет
собственно переходного процесса в цепи с нулевыми начальными усло-
виями и с единственным источником напряжения
)(
до
р
tu
(рис. 10.26, в).
Тогда искомый ток переходного процесса будет равен
до пн
() () ().
ab ab
ab
ititi t
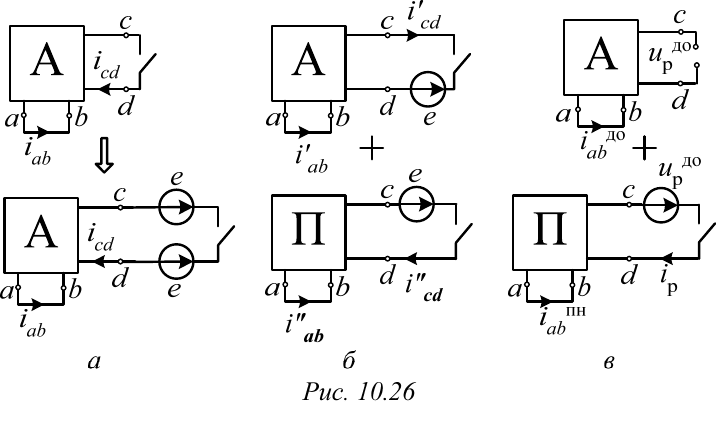
10.2.4.2. Размыкание рубильника (рис. 10.27, а)
Включим параллельно рубильнику два одинаковых источника тока
J(t) противоположного направления. Затем применим принцип наложе-
ния, оставив во второй подсхеме лишь правый источник тока J(t), а в
первой – все остальные источники (рис. 10.27, б). Тогда
() () () и () () ().
ab ab ab cd cd cd
ititit ututut
Подберем J(t) такой величины, каким был ток в ветви рубильника
исходной схемы до коммутации:
до до
p
() () ().
cd
ititJt
Тогда в первой
подсхеме напряжение на зажимах ветви cd и после размыкания рубиль-
ника останется равным нулю:
() 0.
cd
ut
Иными словами, в этой под-
схеме после коммутации сохранится установившийся докоммутацион-
ный режим. Разумеется, в ветви ab будет по-прежнему протекать ток
до
() ().
ab
ab
itit

44
Во второй подсхеме действует единственный источник тока
до
p
() (),Jt i t
который направлен в сторону, противоположную току рубиль-
ника в докоммутационной цепи, причем в остальных ветвях этой подсхемы ни
токов, ни напряжений до коммутации не было. Поэтому ток
)()(
пн
titi
ab
ab
будет определяться при нулевых независимых начальных условиях.
Таким образом, чтобы и в этом случае свести расчет переходного
процесса к нулевым начальным условиям, нужно пройти те же два эта-
па. Сначала следует рассчитать установившийся режим докоммутаци-
онной цепи. При этом определяются как мгновенное значение тока в
интересующей нас ветви, так и
ток в ветви рубильника
до
р
().it
Затем
нужно выполнить расчет собственно переходного процесса в цепи с ну-
левыми начальными условиями и с единственным источником тока
до
р
(),it
направленным как показано на рис. 10.27, в.
И вновь искомый ток переходного процесса будет равен
до пн
() () ().
ab ab
ab
ititi t
Для определения составляющей
)(
пн
ti
ab
в цепи с источниками сложной
формы уже можно применять интеграл Дюамеля. В операторной схеме за-
мещения цепи с нулевыми начальными условиями отсутствуют внутренние
источники (небольшое упрощение расчета операторным методом). Приме-
нение вышеописанного расчетного приема необходимо также в некоторых
вариантах частотного метода, речь о котором пойдет в следующем разделе.
10.5. Расчет переходных процессов
в сложных и специальных схемах
10.5.1. Понятие о частотном методе
Метод аналогичен операторному, но вместо преобразования
Лапласа использует преобразования Фурье – прямое и обратное:
jj
1
(j ) ( ) и () (j ) .
2
tt
F
fte dt ft F e d
Если рассматриваются
переходные процессы с нулевыми независи-
мыми начальными условиями
(а именно о них идет речь в этом разделе), то
можно воспользоваться прямым односторонним преобразованием Фурье:
j
0
(j ) ( ) .
t
F
fte dt
(10.35)
45
Оно позволяет по оригиналу
()
f
t
найти его частотный спектр
(j ).F
Формула (10.35) представляет собой частный случай прямого пре-
образования Лапласа (10.18) при замене р на j
. Поэтому для нахожде-
ния частотных спектров можно использовать таблицы перехода от ори-
гинала к изображению по Лапласу с той же самой заменой (см.
табл. 10.1 и в приложении табл.).
Следует только предварительно проверить, существует ли спектр
данной функции времени. Дело в том, что прямое преобразование
Фурье по сравнению с преобразованием Лапласа
применимо к более
ограниченному классу временных функций. Они должны быть абсо-
лютно интегрируемы, т. е. должен существовать интеграл
0
() .
f
tdt
Например, экспонента
t
e
при
0
имеет изображение по Лапласу,
но ее частотный спектр не может быть определен. Даже частотный
спектр единичного скачка Хевисайда можно найти лишь предельным
переходом от затухающей экспоненты. Действительно, поскольку
j
0
1
,
j
tt
ee dt
а
0
1,
t
e
то 1
1
.
j
Обратное преобразование Фурье
j
1
() (j )
2
t
f
tFed
(10.36)
дает возможность по частотному спектру
(j )F
найти оригинал
().
f
t
А в частном случае, когда частотный спектр представляет собой рацио-
нальную дробь, для этой цели подходит и теорема разложения (10.26) –
опять же с заменой р на j
.
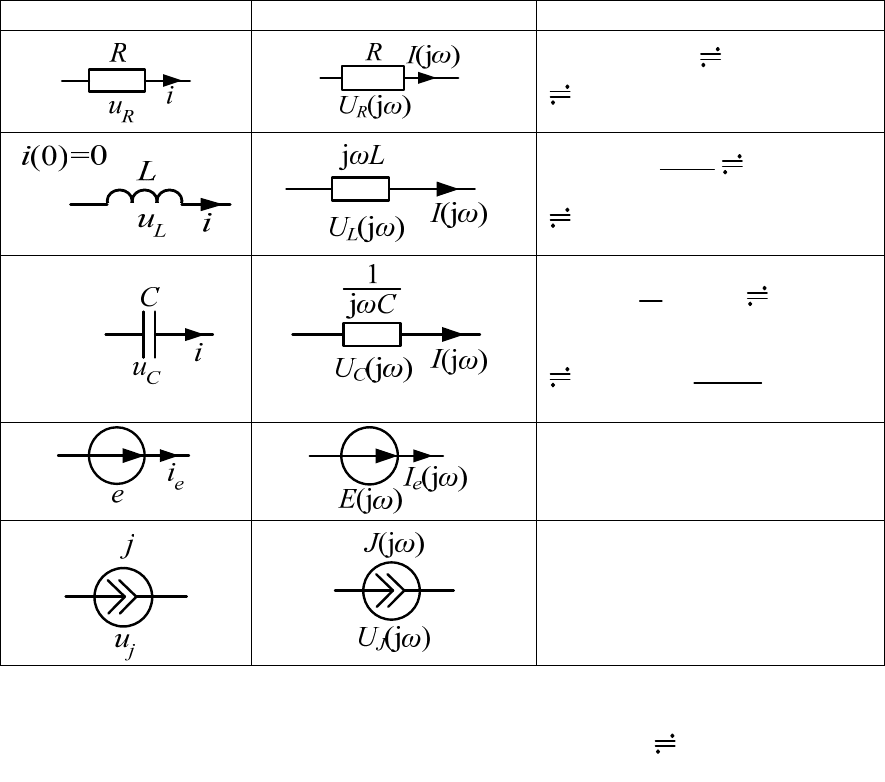
Законы Ома и Кирхгофа в комплексной форме имеют тот же вид,
что и в операторной, но вместо операторных изображений токов и
напряжений в них фигурируют частотные спектры соответствующих
величин, вместо операторного сопротивления – комплексное. Последнее
выглядит в буквенном виде так же, как в комплексном методе, но пред-
ставляет собой не комплексное
число, а функцию частоты.
Первый закон Кирхгофа для узла:
(j ) 0.I
Второй закон Кирхгофа для контура:
(j ) (j ).UE
Закон Ома для ветви R, L, C:
(j ) (j ) (j ).IUZ
Комплексное сопротивление ветви:
(j ) j 1 j .
Z
RL C
46
В общем случае расчет частотным методом аналогичен расчету
операторным, но рассчитывается комплексная схема замещения после-
коммутационной цепи, которая, естественно, подобна операторной схе-
ме (сравните табл. 10.4 с табл. 10.3).
Использование частотного метода целесообразно, когда приходит-
ся производить одновременно какие-нибудь исследования, использую-
щие аналитический аппарат, основанный на преобразовании Фурье.
Примером могут служить системы
автоматического регулирования с
исследованием проблем устойчивости, качества регулирования и т. п.
Преимущества же именно частотного метода сказываются при рас-
четах приближенными методами переходных процессов в цепях высо-
ких порядков, особенно когда частотные характеристики цепи получены
в результате эксперимента.
Таблица 10.4
Элемент схемы Изображение Соотношения
Rtitu
R
)()(
(j ) (j )
R
UIR
dt
tdi
Ltu
L
)(
)(
(j ) (j )j
L
UIL
(0) 0
C
u
0
1
() ()
t
C
ut itdt
C
(j )
(j )
j
C
I
U
C
Напряжение
не зависит от тока
Ток не зависит
от напряжения
Пусть, например, частотный спектр величины на входе некоторой
электрической цепи (рис. 10.23, а) известен:
(j )V
().vt
Тогда ча-
стотный спектр выходной величины
()
f
t
можно найти как
(j ) (j ) (j ).FKV
Здесь
j()
(j ) ( ) ( ) j ( )KKe BM
ком-
47
плексная передаточная функция, которая определяется расчетом ком-
плексной схемы замещения цепи или экспериментально. В свою оче-
редь
22
() (j) () ()KK B M
амплитудно-частотная ха-
рактеристика,
() arg ( ) arctg[ ()/()]Kj M B
фазо-частотная
характеристика,
( ) Re (j ) ( )cos[ ( )]BKK
– вещественная ча-
стотная характеристика,
( ) Im (j ) ( )sin[ ( )]
M
KK
– мнимая
частотная характеристика. Нетрудно заметить, что
()K
и
()B
яв-
ляются четными функциями частоты, а
()
M
и
()
– нечетными.
Если входная величина изменяется по закону единичного скачка
Хевисайда
() 1(),vt t
то ее частотный спектр, как показано выше,
(j ) 1 (j ).V
В этом случае оригинал выходной величины (переход-
ная характеристика) может быть найден как
() ()
f
tht
(j ) (j ) (j ).FK
Тогда по теореме дифференцирования при нуле-
вых начальных условиях
()ht
j(j) (j)FK
и с помощью
(10.36) можно найти
jj[()]
11
() (j ) ( )
22
11
()cos[ ()] ()sin[ ()] .
22
tt
ht K e d K e d
K
td K td
Учитывая соображения о четности и нечетности частотных характе-
ристик, приходим к выводу, что первый интеграл – это четная функция ча-
стоты и поэтому его значения на интервалах
(,0)и (0, )
одинаковы,
а второй интеграл – нечетная функция частоты и равен нулю. Поэтому
0
1
() ()cos[ ()] .ht K t d
Если заменить в этой формуле t на
t
и учесть, что до коммутации
(0)t
цепь не имела запасов энергии, так что
()0,ht
то окажется
0
1
()0 ()cos[() ] .ht K td
Расписывая тригонометрические функции суммы и разности двух
аргументов через синусы и косинусы каждого из углов, получим
0
1
() [ ( )cos( ) ( )sin( )] ,ht B t M t d

48
0
1
0[()cos()()sin()].
B
tM td
После почленного сложения и вычитания этих равенств придем к
формуле
00
22
() ()cos( )] ()sin( )] .ht B t d M t d
И, наконец, взяв интеграл
t
dtthth
0
)()(
с учетом
(0) 0h
, получим:
00
2() 2 ()
( ) sin( ) cos( ) .
BM
ht td td
Эта формула служит основой для приближенного вычисления пе-
реходной функции по вещественной или по мнимой частотной характе-
ристике.
Более подробное знакомство с частотным методом предполагается
в специальных курсах.
10.5.2. Понятие о методе переменных состояния
Уравнениями состояния называют в принципе любую систему
уравнений, описывающих состояние цепи, определяющих ее режим ра-
боты. В более узком смысле этот термин относят к системе дифферен-
циальных уравнений первого порядка, разрешенных относительно про-
изводных. Число уравнений, как и число самих переменных состояния,
равно порядку цепи, который не может превышать суммарного количе
-
ства индуктивностей и емкостей.
Основными переменными состояния следует считать токи в индук-
тивностях (или их потокосцепления) и напряжения на емкостях (или их
заряды). Ведь именно эти переменные отвечают за энергетическое со-
стояние цепи в каждый данный момент времени
M Э
11
(, ),
22
LC
WiWqu
именно их число определяет порядок
системы уравнений, именно эти переменные состояния оказываются
непрерывными величинами (а их начальные условия – независимыми,
которые определяются по законам коммутации).
Метод анализа цепи, основанный на составлении и решении урав-
нений состояния, называют методом переменных состояния. Он ис-
пользует две группы формул. Одна – это собственно уравнения состоя-
ния, т. е. система дифференциальных уравнений первого порядка. В нее

49
в качестве неизвестных входят переменные состояния
(),
x
t
а в качестве
известных – входные величины
().vt
Вторая – алгебраические уравне-
ния, связывающие выходные величины
()
f
t
со входными и с перемен-
ными состояния. В матричной форме система уравнений имеет вид:
;
.
d
dt
xAxBv
fCxDv
Здесь
x, v, f – матрицы-столбцы соответственно переменных состо-
яния, ЭДС и токов источников, выходных токов и напряжений;
А –
квадратная,
В и С – прямоугольные матрицы коэффициентов, которые
выражаются через параметры цепи.
Чтобы записать эти уравнения для простых цепей, достаточно быва-
ет воспользоваться законами Кирхгофа. С применением принципа нало-
жения легко определяются матрицы коэффициентов. В сложных случаях
коэффициенты матричных уравнений определяют с помощью топологи-
ческих методов. А решают их обычно численными методами [9].
Метод переменных
состояния эффективен:
♦ при расчете переходных процессов с большим количеством
накопителей энергии;
♦ при сложных законах изменения
(),et
();
J
t
♦ при анализе многих вариантов с различными параметрами;
♦ при расчете нелинейных и параметрических цепей.
Пример 32.1
Составить уравнения состояния для уже знакомой по классиче-
скому и операторному методам цепи второго порядка (рис. 10.20, а).
Решение
По второму закону Кирхгофа для левого контура и по первому за-
кону для одного из узлов можно записать:
1
2
,.
CC
L
LCL C L
E
udu
di
uuiRL i iC
dt R dt
Отсюда легко находятся первые производные переменных состоя-
ния
и .
L
C
iu
Полученные соотношения и представляют собой урав-
нения состояния:
1
22
1
;
11 1
.
L
L
C
C
L
C
R
di
iu
dt L L
du
iu E
dt C R C R C

50
В матричной форме
1
2
2
1
0
.
1
11
LL
CC
R
ii
LL
d
E
uu
dt
RC
CRC
Для решения дифференциальных уравнений численным методом
следует задать:
1) независимые начальные условия
(0) и (0);
L
C
iu
2) расчетное время
p
;t
3) шаг по времени h.
Расчет можно завершить при
pmax
3,t
когда переходный процесс
практически заканчивается. Строгих критериев для выбора шага нет, но
для первого варианта расчета можно принять
min
3.h
Здесь
max
и
min
соответственно наибольшая и наименьшая из постоянных времени
отдельных ветвей.
В рассматриваемом примере
11
2,5LR
мс,
22
2,5RC
мс –
это взятые по модулю величины, обратные коэффициентам при
L
i
и
.
C
u
Примем
0,75h
мс и
p
7,5t
мс. Тогда при
(0) 0,2 A
L
i
и
(0) 114 B
C
u
решение уравнений состояния
164
400
0
40010
5,2400
5
C
L
C
L
u
i
u
i
dt
d
методом Рунге-Кутта [9] дает значения, приведенные в табл. 10.5.
Таблица 10.5
,
k
t
мс
0 0,75 1,5 2,25 3 3,75 4,5 5,25 6 6,75 7,5
,
k
i
мА
200 398 507 548 546 520 485
4
51 424 405 394
,
k
u
В
164
1
43,8 119,1 96,2 78,1 65,8 58,7 55,7 55,5 56,8 58,8
Этот результат хорошо согласуется с аналитическим решением
примера 10.8.
10.5.3. Понятие об интегрирующих и дифференцирующих цепях
Цепи, напряжение на выходе которых пропорционально производ-
ной или интегралу от входного напряжения, называются, соответствен-
но, дифференцирующими или интегрирующими. Их основное назначе-
ние – формирование электрических сигналов определенной формы.
Схемы простейших дифференцирующих цепей показаны на рис. 10.28.
