Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2
Подождите немного. Документ загружается.

21
Рис. 10.15
б
а
в
д
R
e(0)
i(0)
R
2
R
u
C
(0)
jX
C
R
2
R
2
до
Cm
U
m
E
jX
C
R
2
R
3
пр
m
I
m
E
г
R
C
e(t)
i(t)
R
2
R
u
C
(t)
R
R
2
3
Cp
1
Постоянная интегрирования
св пр
(0) (0) (0) 6,33 7,6sin( 74,7 ) 1 A.Ai i i
Таким образом,
500
( ) 7,6sin(1000 74,7 ) 1 A.
t
it t e
Нетрудно найти и закон изменения
пр
() () .
pt
CC
ut u t Be
В схеме рис. 10.15,г
пр
j j j10 j100 20 j10
Cm C m C
UXERX
j26,5
40 j20 44,72 B.e
пр
Поэтому ( ) 44,7sin(1000 26,5 ) В, а
C
ut t
пр пр
(0) Im( ) 20 В.
CCm
uU
Постоянная интегрирования
пр
(0) (0) 40 20 20 В.
CC
Bu u
Так что
500
( ) 44,7sin(1000 26,5 ) 20 В.
t
C
ut t e
10.2.6. Переходный процесс в цепи второго порядка
Начнем анализ с простейшего случая – свободного процесса в цепи
R, L, C.
22
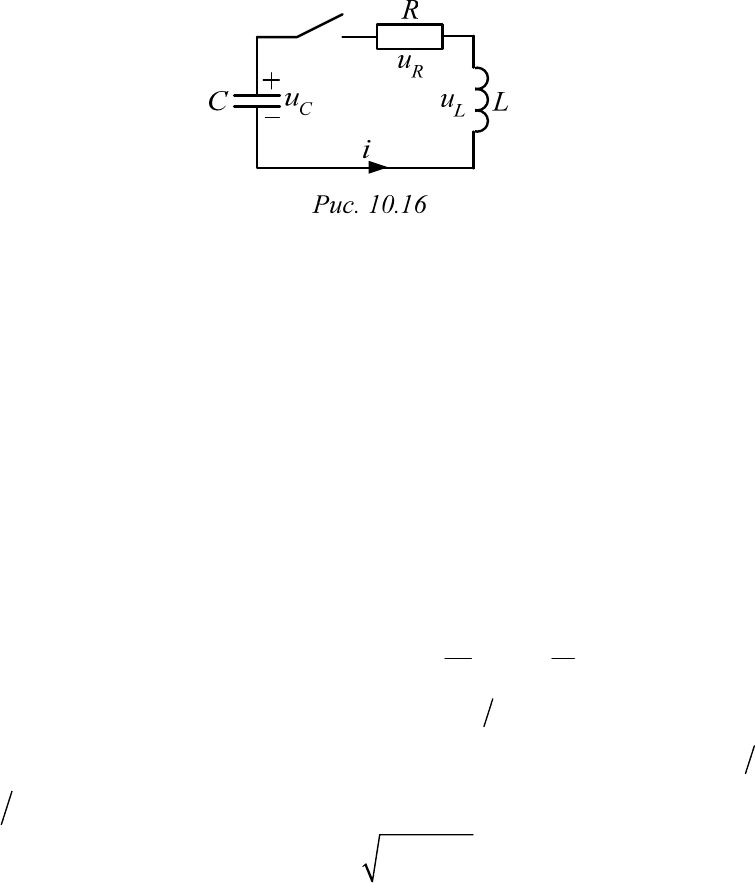
Пример 10.7. Разряд конденсатора С на цепь R, L (рис. 10.16)
Пусть до коммутации конденсатор был заряжен до напряжения
до
0
.
C
uU
Согласно второму закону коммутации напряжение таким же
останется и в момент начала переходного процесса
0
(0) .
C
uU
А ин-
дуктивность, обесточенная до коммутации, сохранит в первый момент
значение тока
до
(0) 0
L
ii
(первый закон коммутации).
В установившемся режиме послекоммутационной цепи конденса-
тор, очевидно, полностью разрядится, вся энергия выделится в виде
тепла в сопротивлении R, поэтому
пр пр
0, 0.
C
ui
Так что
св св
() (), () ().
CC
it i t u t u t
Уравнение, описывающее состояние цепи, получим на основании
второго закона Кирхгофа:
1
0.
LRC
di
uuu L Ri idt
dt C
Характеристическое уравнение
1( ) 0Lp R Cp
имеет два корня.
Если переписать его в виде:
22
0
20,pp
где
2,RL
2
0
1,
L
C
тогда
22
1,2 0
.p
(10.16)
Рассмотрим подробно три возможных случая:
1)
0
,
корни вещественные различные, процесс апериодиче-
ский;
2)
0
,
корни комплексные сопряженные, процесс колеба-
тельный;
3)
0
,
корни равные (кратные), процесс критический.
10.2.6.1. Апериодический разряд конденсатора
Напряжение на конденсаторе при различных корнях можно пред-
ставить в виде суммы двух экспонент:
12
12
.
p
t
p
t
C
uAe Ae
23
Для определения двух входящих в это выражение постоянных ин-
тегрирования необходимо иметь два уравнения. Второе можно получить
из выражения производной, тогда
.
21
2211
tptp
C
eApeAp
dt
du
Напом-
ним, что
.
C
du
i
dt C
Постоянные интегрирования найдем из начальных условий:
12 0
11 2 2
0
(0) ;
(0)
0.
C
C
t
uAAU
du
i
Ap A p
dt C
Отсюда
02 01
12
21 12
,,
Up Up
AA
p
ppp
так что
12
2
1
21
0
;
p
tpt
C
U
upepe
pp
12
12 12
21 21
0
0
;
()
p
tpt ptpt
C
CU p p
du U
iC e e e e
dt p p L p p
.
2
2
1
1
12
0
tptp
L
epep
pp
U
dt
di
Lu
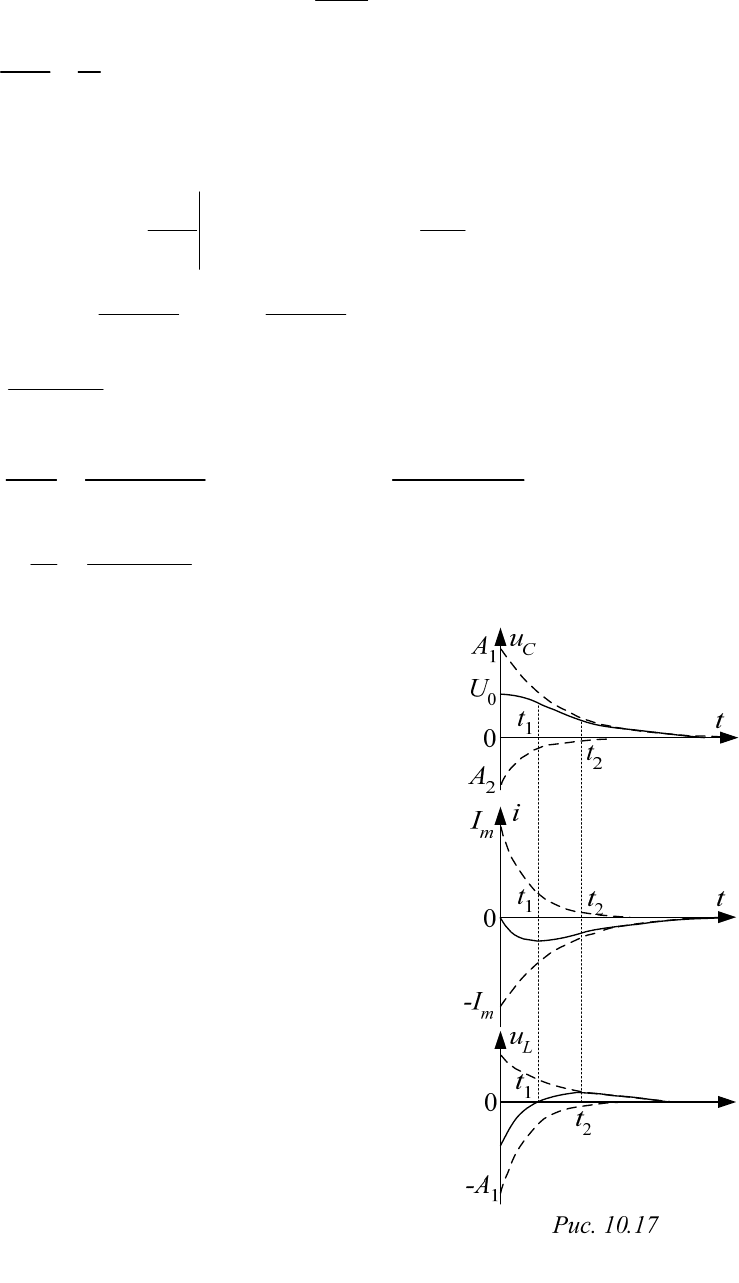
Соответствующие кривые показаны на
рис. 10.17. Здесь можно выделить три ин-
тервала.
Первый начинается при
0,t
когда
0
(0)
C
uU
(кривая
()
C
ut
в этой точке имеет
максимум),
(0) 0,i
0
(0) ,
L
uU
и закан-
чивается при
1
.tt
В этот момент
1
() 0,
L
ut
1
()it
имеет минимум,
1
()
C
ut
точку переги-
ба. На этом интервале
L
u
быстро убывает по
абсолютной величине,
C
u
гораздо медлен-
нее. Ток по абсолютной величине растет.
Мгновенная мощность конденсатора
0 iup
CC
и, следовательно, конденса-
тор в течение всего переходного процесса
отдает свою энергию. Энергия, запасенная в
электрическом поле конденсатора, непре-
рывно расходуется на покрытие тепловых
24
потерь в сопротивлении R, но на первом интервале времени, когда
0,
L
L
pui
часть энергии переходит в энергию магнитного поля ин-
дуктивности.
На втором интервале
12
()ttt
L
u
меняет знак и нарастает, ток
начинает медленно убывать по абсолютной величине, скорость убыва-
ния
C
u
нарастает. При
2
tt
напряжение
L
u
достигает максимума, i
имеет точку перегиба,
L
u
точку перегиба второго порядка.
При
2
tt
затухание всех процессов идет практически с постоян-
ной времени
11
1.p
На втором и третьем интервалах тепловые потери покрываются за
счет энергии и конденсатора, и индуктивности. Когда вся энергия заря-
женного конденсатора
2
2WCU
превратится в тепло, процесс в цепи
закончится.
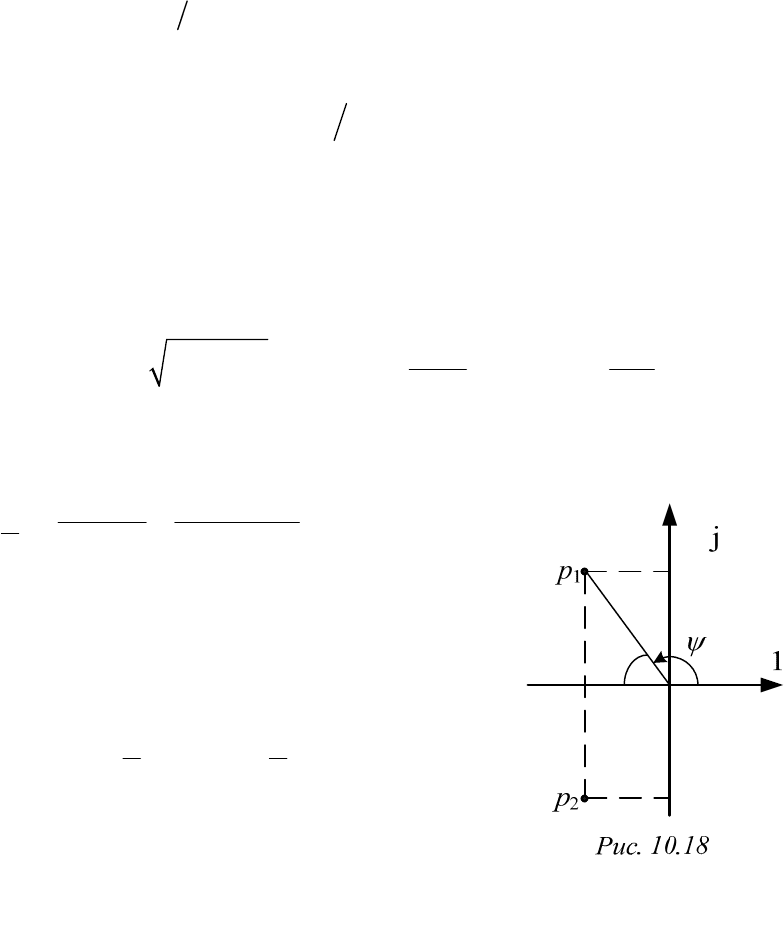
10.2.6.2. Колебательный разряд конденсатора
Корни характеристического уравнения комплексные сопряженные
1,2
j
cв 0
j,pe
где (рис. 10.18)
22
св св
0 св
0
, arctg arcsin .
Поскольку корни различные, то можно использовать уже получен-
ные в п. 10.2.6.1 выражения для постоянных интегрирования:
j
02 00
2
1
21 св
€
.
j2
Up U e
A
A
pp
Таким образом, при комплексных со-
пряженных корнях
1, 2
j
cв 0
jpe
постоянные интегрирования получатся также
комплексными сопряженными
j
12
€
.
A
Ae А
Тогда выражение свободной составля-
ющей можно переписать в следующем виде:
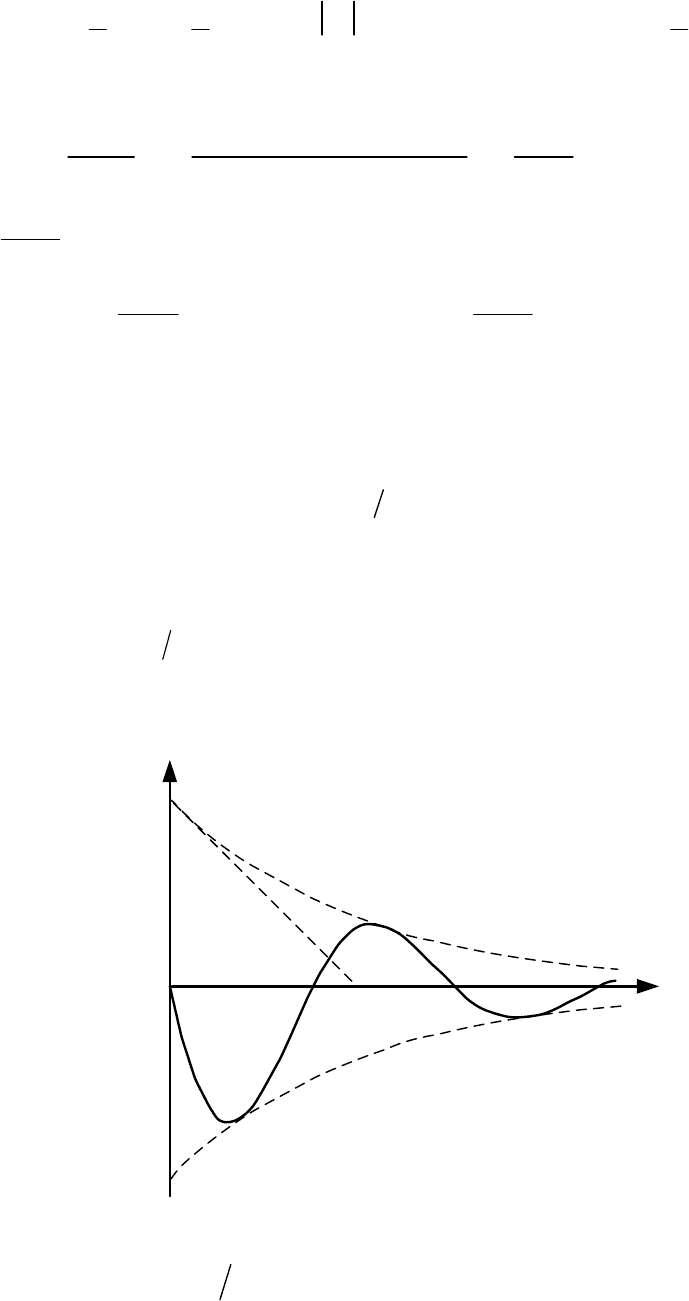
cв
cв
0
cв cв cв cв
( j ) ( j ) j( ) -j( )
jj
tttt
t
Ae e Ae e Ae e e
cв cв cв cв
cos( ) jsin( ) cos( ) jsin( )
t
Ae t t t t
cв
2cos( ).
t
Ae t
25
12 1
1
Re( )
1
12 1
Или 2cosIm()arg.
pt p t p
A
eAe Ae pt A
(10.17)
Преобразуем по формуле (10.17) полученные в п. 10.2.6.1 выраже-
ния для токов и напряжений, имеем:
св св
j( ) j( )
00 0
св
св
0
св
() sin( )
j2 sin
sin( ), где ,
sin
tt
tt
C
t
UU
ee
ut e e t
U
et
00
св св
св
() sin( ), () sin( ).
sin
tt
L
UU
itetutet
L
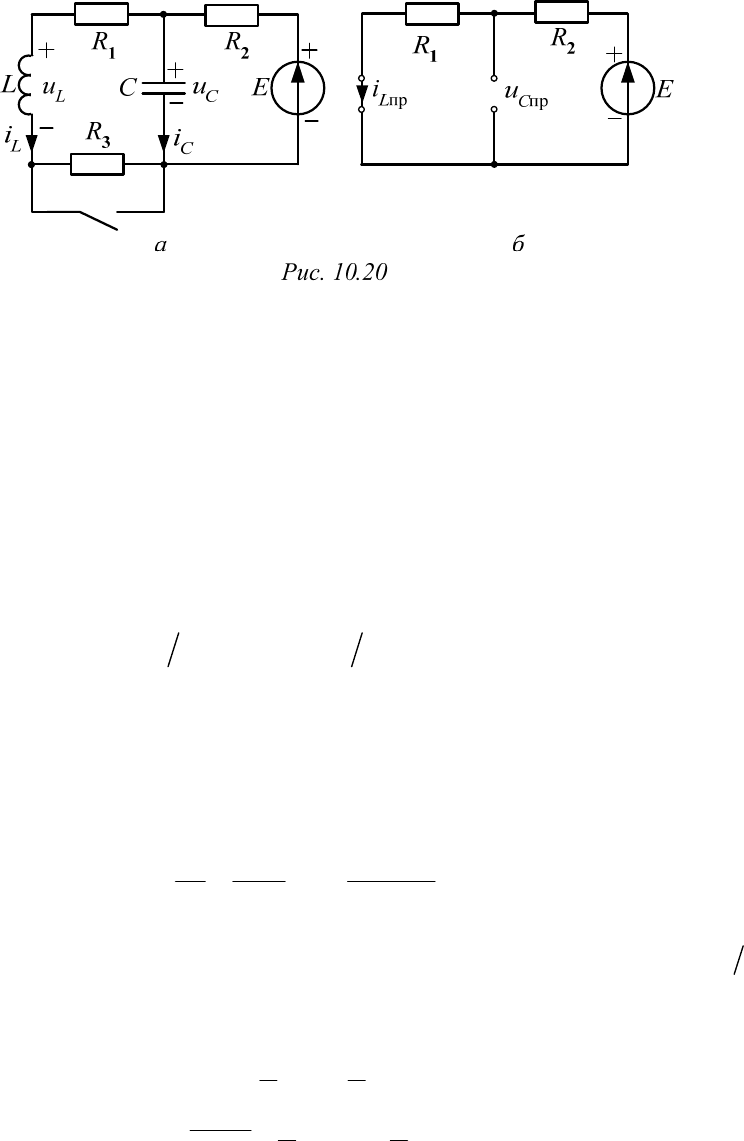
Все кривые представляют собой затухающие синусоиды, которые
(как и обычные синусоиды) отсекают на оси абсцисс одинаковые отрез-
ки, а их амплитуды затухают по экспоненциальному закону. Величина
характеризует скорость затухания и называется коэффициентом зату-
хания. Величина, обратная
св
1
, представляет собой постоянную
времени экспонент, входящих в выражение амплитуд.
Величина
св
называется угловой частотой собственных или сво-
бодных затухающих колебаний. Период свободных затухающих колеба-
ний равен
св св
2.T
0
угловая частота незатухающих колебаний, она равна резо-
нансной частоте контура.
Рис. 10.19
0
t
-I
max
i
T
св
I
max
св
График зависимости
()it
показан на рис. 10.19, где на оси ординат
обозначено
max 0 св
.IU L
Кривая отсекает на оси абсцисс отрезки,

26
равные
св
2,T
а посередине между нулями касается экспоненциальных
огибающих.
Скорость протекания процесса оценивается декрементом колебания
св
св св св
() ( )
T
ititT e
или логарифмическим декрементом колебания
св св св
ln .TT
Чем меньше декремент, тем больше колебаний произойдет до
практического затухания процесса, тем быстрее происходит обмен
энергией между накопителями.
10.2.6.3. Критический процесс
Возникает при равных (кратных) корнях характеристического
уравнения
1,2
0
,p
откуда следует
кр
2/
R
RLC так называемое критическое сопротивление.
Если
кр
,
R
R
то процесс колебательный, если
кр
RR
апериоди-
ческий, а при равенстве этих величин наступает предельный случай
апериодического разряда (граничный режим). При этом решение запи-
сывается в виде:
12 2 1 2
() ( ) , тогда ().
tt
C
C
du
i
ut A Ate A A Ate
dt C
При
0t
имеем
10
(0) ,
C
uAU
21
(0) 0,AAiC
откуда
21 0
.
A
AU
Тогда решение принимает вид:
0
() (1 )
t
C
u
tU te
;
2
00
(
)
tt
tCtUe UteL
;
0
() ( 1) .
t
L
ut U t e
Соответствующие кривые похожи на те, которые приведены на
рис. 10.17, но моменты
12
иtt
легко уточнить:
121
1, 2.ttt
Проверка
0
(0)
L
uU
во всех трех режимах дает правильный ре-
зультат.
Отметим в заключение, что кратные или комплексные корни могут
получиться лишь в цепи с индуктивностью и емкостью. Если же в цепи
второго порядка две катушки или два конденсатора, то корни окажутся
различными вещественными отрицательными.
27
10.2.6.4. Алгоритм расчета сложной цепи второго порядка
Рассмотрим порядок расчета классическим методом на примере
цепи, схема которой показана на рис. 10.20, а.
Пример 10.8
Дано:
164 B;E
1
160 Ом;R
2
250 Ом;R
3
410 Ом;R
0, 4 Гн;L
10 мкФ.С
св пр
:() () ().
CC C
Определить ut ut ut
Решение
1. Находим принужденные составляющие искомых величин, рас-
считывая послекоммутационную цепь в установившемся режиме
().t
Ее схема показана на рис. 10.20, б (для постоянного тока ин-
дуктивность – это закоротка, конденсатор – разрыв цепи). Тогда
пр 12
164 160 250 0,4 A.
L
iERR
пр пр 1
0,4 160 64 B.
CL
uiR
2. Находим корни характеристического уравнения, начертив пред-
варительно операторную схему замещения послекоммутационной цепи
без источников. Такая схема (рис. 10.6) была рассмотрена в приме-
ре 10.2, где и выведено характеристическое уравнение (10.14). Перепи-
шем его в виде:
2
112
22
1
0.
RRR
pp
LRC RLC
И подставим числа:
2j127,6
1, 2
800 410000 0. Тогда 400 j500 640 1 c.pp p e
3. Записываем в общем виде выражение свободных составляющих
искомых величин и их производных в виде суммы двух экспонент:
12
12
12
12
2
св
св
1
;
.
pt p t
C
p
tpt
C
uAeAe
du
A
pe A p e
dt
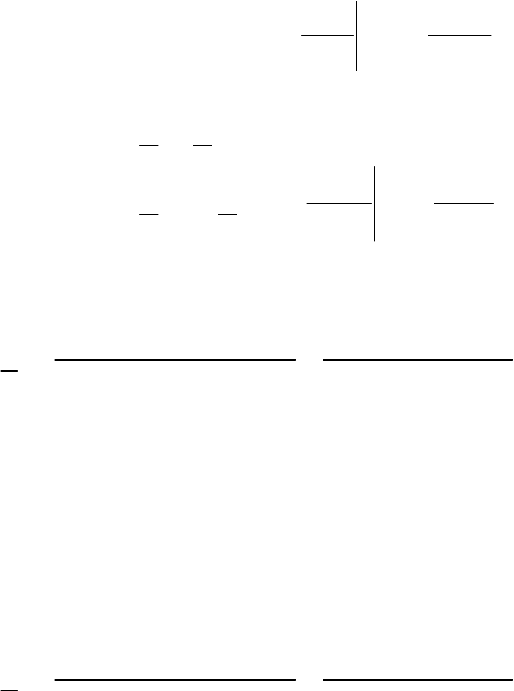
28
4. Находим независимые начальные условия, предварительно рас-
считав установившийся режим докоммутационной цепи. Эта работа бы-
ла проделана в примере 10.1. Результат:
до до
(0) 0,2 A; (0) 114 B.
L
CC
ii u u
5. Определяем зависимое начальное условие
(0),
C
i
рассматривая
послекоммутационную цепь в момент
0t
(рис. 10.5). В том же приме-
ре эта величина найдена
(0) 0.
C
i
В дальнейших расчетах нам понадобится начальное значение про-
изводной:
,0
)0(
0
C
i
dt
du
C
t
C
6. Находим постоянные интегрирования из начальных условий.
12
св пр
св
12
12
0
(0) (0) (0) 144 64 50;
(0)
0.
CCC
CC
t
AAu u u
du i
Ap A p
dt C
Отсюда
'
2 св св
(0)
j38,7
2
1
21
(0)
( 400 j500) 50
€
25 j20 32 B .
2( j500)
CC
pu u
AeA
pp
7. Подставляем постоянные в формулу п. 3 и приводим ее к виду
затухающей косинусоиды с помощью преобразования (10.17):
B.)7,38500cos(64
3232)(
400
)500j400(7,38j)500j400(7,38j
св
te
eeeetu
t
tt
C
Отсюда
'
2 св св
(0)
j38,7
2
1
21
(0)
( 400 j500) 50
€
25 j20 32 B .
2( j500)
CC
pu u
A
eA
pp
8. Подставляем постоянные в формулу п. 3 и приводим ее к виду
затухающей косинусоиды с помощью преобразования (10.17):
B.)7,38500cos(64
3232)(
400
)500j400(7,38j)500j400(7,38j
св
te
eeeetu
t
tt
C
9. Записываем решение, суммируя принужденную и свободную со-
ставляющие.
400
( ) 64 64 cos(500 38,7 ).
t
C
ut e t

29
К достоинствам классического метода следует отнести его просто-
ту и наглядность, к недостаткам – необходимость вычисления зависи-
мых начальных условий и принужденных составляющих, составления
характеристического уравнения – и все это с использованием разных
схем замещения рассматриваемой цепи.
10.3. Операторный метод расчета
переходных процессов в линейных цепях
10.3.1. Преобразование Лапласа и его свойства
Сущность метода в том, что функции вещественного переменно-
го t, называемой оригиналом
(),
f
t
ставится в соответствие такая функ-
ция комплексного переменного р, называемая изображением
(),Fp
что
интегралы и производные от оригинала по t заменяются алгебраически-
ми функциями р. Поэтому система интегро-дифференциальных уравне-
ний для оригиналов заменяется системой алгебраических уравнений для
изображений, которая решается гораздо проще. Затем возвращаются к
оригиналам.
Соответствие устанавливается прямым односторонним преобразо-
ванием Лапласа:
f(t)
0
() ()
p
t
F
pftedt
,
(10.18)
где
– знак соответствия.
В табл. 10.1 приведены некоторые свойства этого преобразования.
Из формул (10.21) при
(0) 0
f
и (10.22) видно, что p представляет
собой оператор, умножение и деление на который изображения соот-
ветствуют дифференцированию и интегрированию оригинала. Отсюда и
название метода.
В табл. 10.2 даны примеры соответствия оригиналов и изображе-
ний. Первый пример легко получить непосредственно с помощью пре-
образования Лапласа (10.18). Второй – на основе первого с учетом со-
отношения
t
AdtAt
0
и с использованием теоремы интегрирования
(10.22). Третий опять же на базе первого и теоремы смещения (10.24).
А два последних получаются из предыдущего после замены а на jω и
использования свойства коммутативности (10.20).
30
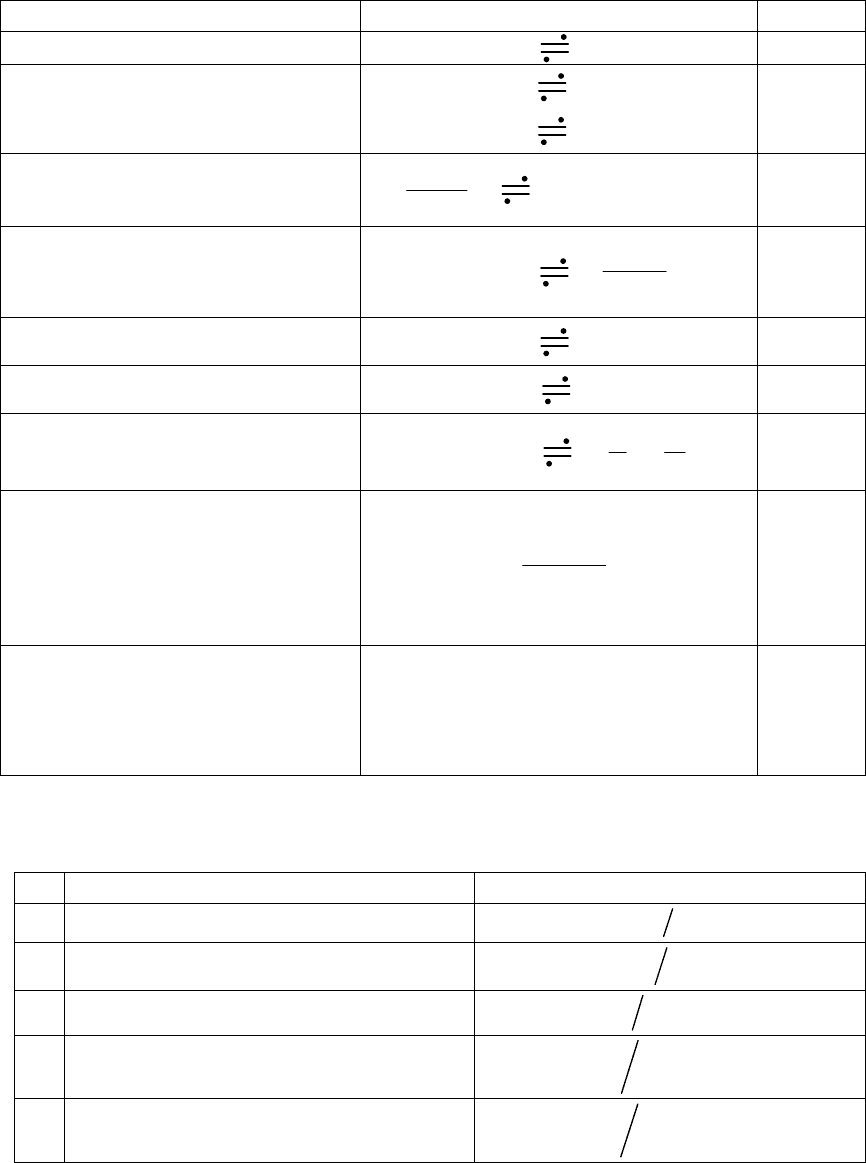
Таблица 10.1
Свойство Формула Номер
Свойство линейности
()
kk
a
fp
)( pFa
k
k
(10.19)
Свойство
коммутативности
Re ( )
f
t
Re ( )Fp
Im ( )
f
t
Im ( )Fp
(10.20)
Теорема
дифференцирования
()df t
dt
)0()(
f
p
pF
(10.21)
Теорема
интегрирования
t
dttf
0
)(
p
pF )(
(10.22)
Теорема запаздывания
)(
0
ttf
)(
0
pFe
pt
(10.23)
Теорема смещения
at
etf
)(
)( a
p
F
(10.24)
Теорема
подобия
)(a
t
f
a
p
F
a
1
(10.25)
Теорема разложения
для многочленов А(р) и В(р)
степеней m и n
соответственно (m < n)
Если
F(p) = A(p)/B(p), то
n
k
tp
k
k
k
e
pB
pA
tf
1
)('
)(
)(
, где
()0,
k
Bp
k
p
– различны
(10.26)
Теорема
о предельных
соотношениях
)(lim)]([lim
),(lim)]([lim
0
0
tfppF
tfppF
tp
tp
(10.27)
Таблица 10.2
№ Оригинал Изображение
1
const
A
A
p
2
A
t
2
A
p
3
at
A
e
A
pa
4
cos( )
A
t
22
A
pp a
5
sin( )
A
t
22
A
pa
Расширенная таблица соответствия лапласовых изображений и
оригиналов приведена в приложении.
