Ещин Е.К. Моделирование систем управления электромеханическими объектами
Подождите немного. Документ загружается.

81
,f
f
f
f
rvru
0
2
0
1
0
=
Ψ∂
∂
+
Ψ∂
∂
раскрывая которые относительно
α, получим
(
)
,
p
M
R
p
rurvn
r
n
22
3
3
2
Ψ+Ψω
+
ω
ω
=α
(
)
,
p
M
R
p
s
uru
s
vrvn
r
n
ΨΨ+ΨΨω
+
ω
ω
=α
3
2
3
(
)
(
)
.
UUp
M
R
rur
v
n
s
u
sv
sv
s
u
s
22
3
3
2
Ψ+Ψω+Ψ−Ψ
=α
Первые два регулятора обеспечивают идеально одинаковое качество управления (см.рисунки
ниже). При реализации последнего система неустойчива, что указывает на некорректность задачи управ-
ления
56
. Использование регуляризующей процедуры с введением стабилизирующего функционала обес-
печивает устойчивость системы и необходимое качество управления.
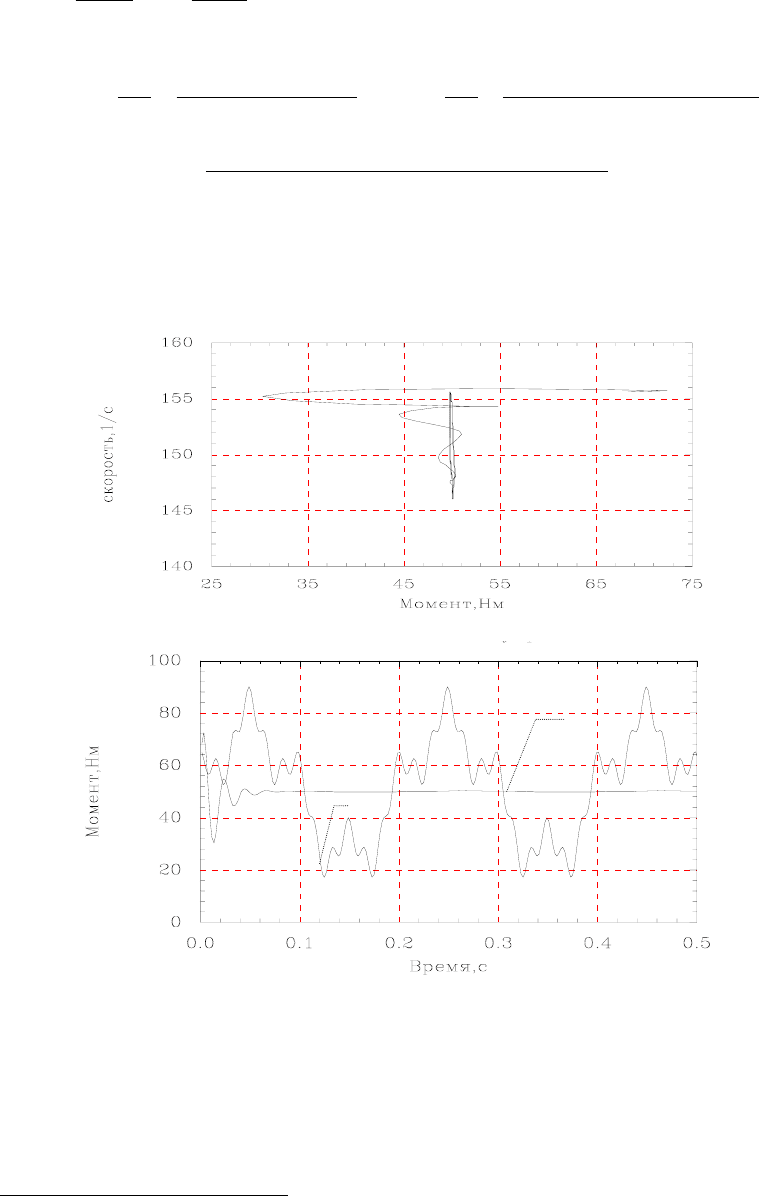
Стабилизация электромагнитного момента АД (устойчивый вариант)
Изменение момента сопротивления (Мс) и электромагнитного момента АД (М) при его стабилизации
56
Тихонов А.Н.,Арсенин В.Я. Методы решения некорректных задач. -М.: Наука,1974. -224 c.

82
10.ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
10.1.ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ
Вариационными задачами на условный экстремум называются задачи, в которых требуется найти
экстремум функционала
v, причем на функции, от которых зависит функционал, наложены некоторые
ограничения
57
.
Например, требуется исследовать на экстремум функционал
[]
()
dxy,...,y,y,y,...,y,y,xFy,...,y,yv
x
o
x
nnn
∫
′′′
=
1
212121
при наличии условий
()
0
21
=ϕ
ni
y,...,y,y,x
, (i=1,2,…,m; m<n).
Алгоритм определения экстремалей в этом случае дается следующей
теоремой.
Функции
y
1
,y
2
,…,y
n
, реализующие экстремум функционала v при наличии условий
()
0
21
=
ϕ
ni
y,...,y,y,x
удовлетворяют при соответствующем выборе множителей λ
i
(x) (i=1,2,…,m)
уравнениям Эйлера, составленным для функционала
()
∫∫
∑
∗
=
∗
=
ϕλ+=
1
0
1
0
1
x
x
x
x
m
i
ii
dxFdxxFv
.
Функции
λ
i
(x) и y
i
(x) определяются из уравнений Эйлера
0=−
∗
′
∗
jj
yy
F
dx
d
F
(j=1,2,…,n)
и
ϕ
i
=0 (i=1,2,…,m).
В самом деле. Основное условие экстремума
δv=0 приобретает в данном случае вид
()
0
1
0
1
=
′
δ+δ
∫
∑
=
′
dxyFyF
x
x
n
j
jyjy
jj
.
Последнее выражение можно преобразовать к виду
0
1
0
1
=δ
−
∫
∑
=
′
dxyF
dx
d
F
j
x
x
n
j
yy
jj
.
Вариации
δy
j
должны удовлетворять следующим условиям, полученным путем варьирования
уравнений связи
ϕ
i
=0
0
1
=δ
∂
ϕ∂
∑
=
j
n
j
j
i
y
y
(i=1,2,…,m).
Умножая каждое из этих уравнений на
λ
i
(x)dx и интегрируя в пределах от x
0
до x
1
получим
57
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.:Наука, 1969. –424 с.
83
() ()
m,...,,idxy
y
x
j
n
j
j
i
x
x
i
21 0
1
1
0
==δ
∂
ϕ∂
λ
∑
∫
=
Складывая эти уравнения с уравнением
0
1
0
1
=δ
−
∫
∑
=
′
dxyF
dx
d
F
j
x
x
n
j
yy
jj
будем иметь
()
0
1
0
11
=δ
′
∂
∂
−
∂
ϕ∂
λ+
∂
∂
∫
∑∑
==
dxy
y
F
dx
d
y
x
y
F
j
x
x
n
j
j
m
i
j
i
i
j
или, если ввести обозначение
()
∑
=
∗
ϕλ+=
m
i
ii
xFF
1
получим
0
1
0
1
=δ
′
∂
∂
−
∂
∂
∫
∑
=
∗∗
dxy
y
F
dx
d
y
F
j
x
x
n
j
jj
откуда, после некоторых дополнительных заключений будем иметь, что функции, реализующие
условный экстремум функционала v и множители λ
i
(x) должны удовлетворять системе уравнений
()
()()
.m,...,,iy,...,y,y,x
,n,...,,j
y
F
dx
d
y
F
ni
jj
21 0
21 0
21
==ϕ
==
′
∂
∂
−
∂
∂
∗∗
Заметим, что рассмотренные связи носят название голономных. Связи вида
()
0
2121
=
′′′
ϕ
nni
y,...,y,y,y,...,y,y,x
, т.е. содержащие производные экстремалей и записываемые в виде
дифференциальных уравнений называются неголономными. Процедура отыскания экстремалей для та-
кого вида связей аналогична процедуре, рассмотренной выше.
10.2.ПРИМЕР. УПРАВЛЕНИЕ АСИНХРОННЫМ ЭЛЕКТРОДВИГАТЕЛЕМ
Рассмотрим задачу об обеспечении минимума целевого функционала
()
−=
∫
t
t
dtMMinfJ
0
2
3
или
() () () ()()
dttttt
L
k
pMJ
t
t
rvsusvru
s
r
∫
ΨΨ−ΨΨ
′
−=
0
2
3
2
3
Будем полагать, что реализуется частотный способ управления асинхронным электродвигателем
и поэтому
необходимо определить связи (определяющие аналитическую конструкцию оптимального
регулятора)
между управляющими воздействиями (относительными значениями частоты тока статора
(α) и напряжения (γ)),
фазовыми координатами, характеризующими состояние электродвигателя
(потокосцепления, скорость вращения ротора)
и его параметрами
84
Исходные уравнения движения АД в синхронной системе вращающихся координат U,V образуют
систему дифференциальных связей, описывающих состояние АД
()
()
=Ψω−αω+Ψ
′
−Ψ
′
+
Ψ
=Ψω−αω−Ψ
′
−Ψ
′
+
Ψ
=Ψαω+Ψ
′
−Ψ
′
+−
Ψ
=Ψαω−Ψ
′
−Ψ
′
+−
Ψ
.pk
L
R
L
R
dt
d
,pk
L
R
L
R
dt
d
,k
L
R
L
R
U
dt
d
,k
L
R
L
R
U
dt
d
runsvs
r
r
rv
r
r
rv
rvnsus
r
r
ru
r
r
ru
sunrvr
s
s
sv
s
s
sv
sv
svnrur
s
s
su
s
s
su
su
0
0
0
0
Формулируя задачу как классическую на условный экстремум с подвижными концами, образуем
вспомогательную функцию
()
()
()
() ()
()
()
,pk
L
R
L
R
dt
d
t
pk
L
R
L
R
dt
d
t
k
L
R
L
R
U
dt
d
t
k
L
R
L
R
U
dt
d
t
L
k
pMH
runsvs
r
r
rv
r
r
rv
rvnsus
r
r
ru
r
r
ru
sunrvr
s
s
sv
s
s
sv
sv
svnrur
s
s
su
s
s
su
su
rvsusvru
s
r
Ψω−αω+Ψ
′
−Ψ
′
+
Ψ
λ+
+
Ψω−αω−Ψ
′
−Ψ
′
+
Ψ
λ+
+
Ψαω+Ψ
′
−Ψ
′
+−
Ψ
λ+
+
Ψαω−Ψ
′
−Ψ
′
+−
Ψ
λ+
+
ΨΨ−ΨΨ
′
−=
4
3
2
1
2
3
2
3
где λ
i
(t) - множители Лагранжа, и далее систему уравнений Эйлера
0 0 =
′
∂
∂
−
∂
∂
=
′
∂
∂
−
∂
∂
t
sv
sv
t
su
su
U
H
dt
d
U
H
,
U
H
dt
d
U
H
,
0 0 =
′
Ψ∂
∂
−
Ψ∂
∂
=
′
Ψ∂
∂
−
Ψ∂
∂
t
sv
sv
t
su
su
H
dt
dH
,
H
dt
dH
,
где
Ψ
∂
∂
=
′
Ψ∂
∂
Ψ
∂
∂
=
′
Ψ∂
∂
dt
d
HH
,
dt
d
HH
sv
t
sv
su
t
su
.
Из первых двух условий следует: λ
1
(t)=0, λ
2
(t)=0. Учитывая это, из третьего и четвертого получа-
ем:
() ()
rv
r
MM
R
p
t Ψ−=λ
33
3
,
() ()
.MM
R
p
t
ru
r
Ψ−−=λ
34
3
85
Используя полученные связи в выражении для H и, учитывая условия трансверсальности (H
≡
0),
пишем
()
() ()
() ()
.pk
L
R
L
R
dt
d
MM
R
p
pk
L
R
L
R
dt
d
MM
R
p
L
k
pMH
runsvs
r
r
rv
r
r
rv
ru
r
rvnsus
r
r
ru
r
r
ru
rv
r
rvsusvru
s
r
0
3
3
2
3
3
3
2
3
=
Ψω−αω+Ψ
′
−Ψ
′
+
Ψ
Ψ−−
−
Ψω−αω−Ψ
′
−Ψ
′
+
Ψ
Ψ−+
+
ΨΨ−ΨΨ
′
−=
Разрешая последнее относительно α, получим последовательно
() ()
()
.p
dt
d
R
p
p
dt
d
R
p
MMH
run
rv
ru
r
rvn
ru
rv
r
0
3
3
3
=
Ψω−αω+
Ψ
Ψ−
−
Ψω−αω−
Ψ
Ψ++=
() ()
()
.
R
p
p
dt
d
R
p
R
p
p
dt
d
R
p
MMH
ru
r
n
rv
ru
r
rv
r
n
ru
rv
r
0
33
33
2
2
3
=Ψω−αω−
Ψ
Ψ−
Ψω−αω−
Ψ
Ψ++=
() ()
.
dt
d
dt
d
R
p
MM
R
p
p
rv
ru
ru
rv
r
r
r
n
Ψ
Ψ−
Ψ
Ψ++=Ψω−αω
33
3
2
()
.
R
p
dt
d
dt
d
R
p
MM
p
r
r
n
rv
ru
ru
rv
r
n
2
3
3
3
Ψω
Ψ
Ψ−
Ψ
Ψ++
+
ω
ω
=α
При отсутствии электромагнитных переходных явлений (статический режим) это выражение
приводится к виду:
()
.,
p
MM
Rp
rvrur
r
n
r
n
222
2
3
3
Ψ+Ψ=Ψ
Ψω
+
+
ω
ω
=α
Использование найденных выражений для определения значений активных сопротивлений цепи
ротора предполагает наличие информации об его электромагнитном моменте, потокосцеплении ротора,
скорости вращения ротора и пр., т.е. использование полученных аналитических конструкций возможно
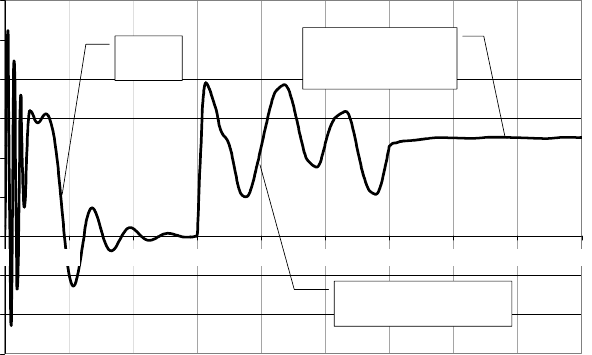
после выполнения предварительного этапа определения значений этих величин. На рисунке ниже приве-
ден характер изменения электромагнитного момента асинхронного электродвигателя последовательно в
режимах пуска без нагрузки, работы с пульсирующей нагрузкой и управляемом режиме работы с целью
стабилизации значения электромагнитного момента.
86
-300
-200
-100
0
100
200
300
400
500
600
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
t,C
M,Hm
Работа с пульсирующей
нагрузкой
Пуск без
нагрузки
Стабилизация
электромагнитного
момента
Далее приведен текст исходного модуля на Visual Basic для среды Excel реализующего задачу
управления состоянием асинхронного электродвигателя:
' Учебные задачи кафедры ВТ
' Управление состоянием асинхронного электродвигателя
'============================================================
Option Explicit
Public j, N, i As Integer
Public Y0(), Y0I(), Yz(), Y0z(), _
Y(), F(), _
k1(), k2(), _
k3(), k4() As Single
Public x, X0z, X0, _
Xk, h, Hz, _
eps As Single
Public Rs, Rr, Xs, Xr, Xm, _
l1, l2, lm, w, _
lps, lpr, ks, kr, _
p, GD2, c, Tvn, Tvu, _
alfa, Mc As Single
'=========================================================
Sub AD()
Dim Prom As Single
Dim Mess As String
N = 5
ReDim Y0(N), Y0I(N), Yz(N), Y0z(N), _
Y(N), F(N), _
k1(N), k2(N), k3(N), k4(N)
Mess = MsgBox("Управление электромагнитным моментом АД", , _
" Учебные задачи кафедры ВТ ")
eps = 0.0001: h = 0.002: Hz = h
X0 = 0: X0z = X0: h = Hz: Xk = 1
For i = 1 To N
Y0(i) = 0
Next i
87
Y0(5) = 0.0001
'=========================================================
Tvn = 0.3 ' Время подачи пульсирующей нагрузки на вал АД
Tvu = 0.6 ' Время включения управления состоянием АД
'=========================================================
' Параметры для двигателя ВРП160М4
Rs = 0.516: Rr = 0.406
Xs = 1.419: Xr = 1.1
Xm = 35: p = 2
GD2 = 0.7
' Коэффициенты для уравнений движения АД
l1 = Xs / 314
l2 = Xr / 314
lm = Xm / 314
lps = l1 + l2 * lm / (l2 + lm)
lpr = l2 + l1 * lm / (l1 + lm)
ks = lm / (lm + l1)
kr = lm / (lm + l2)
c = 3 * p * ks / (2 * lpr)
MsgBox "Нажмите OK и ждите!"
Shet ' Основная обработка и подготовка данных
With Sheets("Лист3")
End With
MsgBox "Все!"
End Sub
'=========================================================
Sub Shet()
Dim L, K As Integer
Worksheets("Лист3").Select
Worksheets("Лист3").Range("A1: H1000").Clear
j = 2
With Worksheets("Лист3")
For K = 1 To N
.Cells(1, K + 1) = Y0(K)
Next K
End With
x = X0
While x <= Xk
Runge (x)
For i = 1 To N: Yz(i) = Y(i): Next i
h = h / 2
Runge (x)
For i = 1 To N: Y0(i) = Y(i): Next i
x = x + h
Runge (x)
L = 0
For i = 1 To N
If Abs(Yz(i) - Y(i)) < eps * Abs(Yz(i)) Then
L = L + 1
88
End If
Next i
If L = N Then
With Worksheets("Лист3")
For K = 1 To N
.Cells(j, K + 1) = Y(K)
Y0(K) = Y(K)
Y0z(K) = Y(K)
Next K
.Cells(j, 1) = x
.Cells(j, 7) = c * (Y(3) * Y(2) - Y(1) * Y(4))
End With
x = x + h
h = Hz
j = j + 1
Else
x = x - h
'MsgBox "h=" & Str(h)
End If
Wend
End Sub
'=========================================================
Sub Uravnen()
' Формирование момента сопротивления
If x <= Tvn Then
Mc = 0
Else
Mc = 250 + 100 * Sin(6.28 * 10 * x) + 50 * Sin(6.28 * 5 * x)
End If
' Формирование управляющего воздействия
If x <= Tvu Then
alfa = 1
Else
alfa = p * Y(5) / 314 + Rr * ((250 + c * (Y(3) * Y(2) - Y(1) * Y(4)))) /
(3 * p * 314 * (Y(3) ^ 2 + Y(4) ^ 2))
End If
' Уравнения движения АД
F(1) = 537 * alfa - Rs / lps * Y(1) + Rs / lps * kr * Y(3) + 314 * alfa *
Y(2)
F(2) = -Rs / lps * Y(2) + Rs / lps * kr * Y(4) - 314 * alfa * Y(1)
F(3) = -Rr / lpr * Y(3) + Rr / lpr * ks * Y(1) + (314 * alfa - p * Y(5)) *
Y(4)
F(4) = -Rr / lpr * Y(4) + Rr / lpr * ks * Y(2) - (314 * alfa - p * Y(5)) *
Y(3)
F(5) = 4 * (c * (Y(3) * Y(2) - Y(1) * Y(4)) - Mc) / GD2
End Sub
'=========================================================
Sub Runge(x As Single)
x = X0
For i = 1 To N: Y(i) = Y0(i): Next i: Uravnen

89
For i = 1 To N: k1(i) = h * F(i): Next i
x = X0 + h / 2
For i = 1 To N: Y(i) = Y0(i) + k1(i) / 2: Next i: Uravnen
For i = 1 To N: k2(i) = h * F(i): Next i
For i = 1 To N: Y(i) = Y0(i) + k2(i) / 2: Next i: Uravnen
For i = 1 To N: k3(i) = h * F(i): Next i
x = X0 + h
For i = 1 To N: Y(i) = Y0(i) + k3(i): Next i: Uravnen
For i = 1 To N: k4(i) = h * F(i): Next i
For i = 1 To N
Y(i) = Y0(i) + (k1(i) + 2 * k2(i) + 2 * k3(i) + k4(i)) / 6
Next i
End Sub
'=========================================================
11.ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
11.1.ПРИМЕР. КВАЗИОПТИМАЛЬНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМ ЭЛЕКТРОДВИГАТЕЛЕМ
Практическая реализация идеальных оптимальных управлений маловероятна по многим причи-
нам. Главные из них - проблема обеспечения точности вычисления абсолютного скольжения на основе
измеренных параметров состояния и проблема физической реализации датчиков для измерения парамет-
ров состояния электродвигателя применительно к условиям эксплуатации горных машин.
Однако, если цель управления электроприводом - стабилизация состояния АД, выражаемая, на-
пример, в виде уже рассмотренного нами функционала
()
()
−=
∫
∈γα∀
t
U,
t
dtMMinfJ
0
2
3
58
,
то можно показать, что во всех управляемых режимах работы двигателя, вплоть до опрокидыва-
ния, необходимо выполнение условия β=const, т.е. обеспечение линейной зависимости
(
)
р
f
α
=α
, кото-
рая в области рабочих скоростей с достаточной степенью точности аппроксимируется также линейной
зависимостью, но проходящей через начало координатной системы α, α
р
р
kα=α
,
причем k=const и находится из условия t=0, α=1, α
р
=α
рн
- начальному относительному значению
угловой скорости вращения ротора при частоте тока в статоре, равной номинальной.
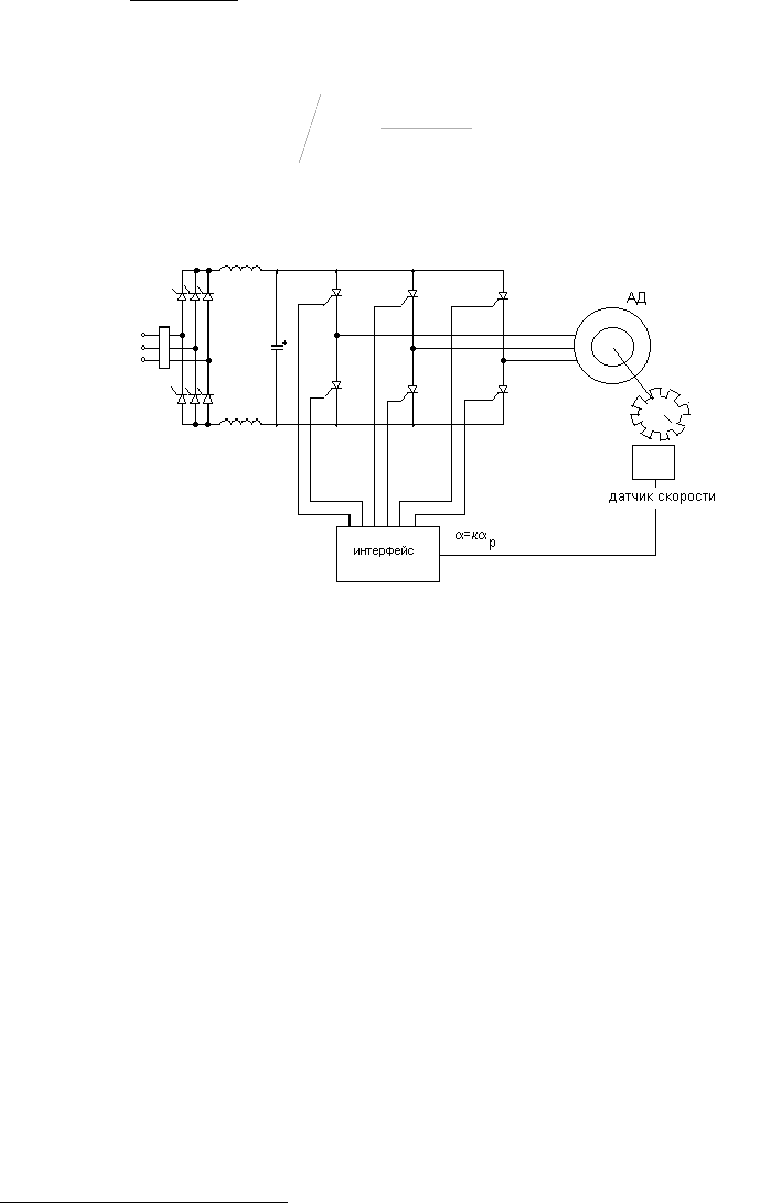
Главным достоинством этого выражения является то, что в отличие от полученных аналитиче-
ских конструкций оптимальных регуляторов его можно реализовать точно
. Это достигается путем зада-
ния определяемого количества зубцов или отверстий (N
з
) на вращающемся элементе дискретного датчи-
ка скорости по формуле
58
inf от infimum – нижняя грань.
90
()
n
pncn
sn
kkf
N
−
=
1
60
3
,
где f
n
- номинальная частота сети, Гц; k
пс
- коэффициент пересчетной схемы тиристорного преоб-
разователя частоты; k
p
- коэффициент кратности, который определяется следующим образом:
()
−
=
n
ncn
p
sn
kf
fracintk
1
60
1
,
int() -выделяет целую часть выражения; frac() - выделяет дробную часть выражения; n - синхрон-
ное число оборотов АД, об/мин; s
n
- номинальное скольжение.
Например, при f
n
=50 Гц; k
пс
=6, k
p
=4, n =1500 об/мин; s
n
=0.02, значение N
3
=49.
Использование такого варианта управления привлекательно простотой реализации
59
, однако, сле-
дует учесть, что если при этом изменять динамическую составляющую амплитуды напряжения АД в со-
ответствии с частотой тока статора, то возникнет потеря устойчивости двигателя, который в зависимости
от величины коэффициента k может или остановиться, или пойти “вразнос”. Это объяснимо, поскольку в
этом варианте система оказывается замкнутой положительной обратной связью по скорости.
Рассмотрим процессы, происходящие в системе при изменении момента сопротивления на валу
АД. При росте этого момента и снижении частоты вращения ротора положительная обратная связь по
скорости в соответствии со связью
р
k
α
=α
обеспечит уменьшение частоты тока статора (синхронной
частоты вращения поля статора), что, в свою очередь, приведет к еще большему уменьшению частоты
вращения ротора. При сохранении амплитуды питающего напряжения постоянной уменьшение частоты
его приведет к росту электромагнитного момента АД и приближению его к значению момента сопротив-
ления.
Снижение частоты вращения ротора будет происходить до тех пор, пока не установится равенст-
во моментов. Таким образом, статическая механическая характеристика новой системы будет сущест-
венно отличаться от естественной механической характеристики АД. Пример характеристики для двига-
теля ВРП160М4 показан на рисунке.
59
Ещин Е.К. Вариант частотного управления асинхронным электроприводом горных машин // Элек-
тротехника, -1996, №1
