Ещин Е.К. Моделирование систем управления электромеханическими объектами

Подождите немного. Документ загружается.

111

U = -1

End If

If Y(1) > 0 And Y(2) < 0 And Y(1) > Y(2) ^ 2 / 2 Then

U = -1

End If

If Y(1) > 0 And Y(2) < 0 And Y(1) <= Y(2) ^ 2 / 2 Then

U = 1

End If

'----------------------------------------------------------

If Y(1) < 0 And Y(2) < 0 Then

U = 1

End If

If Y(1) < 0 And Y(2) > 0 And Y(1) < -Y(2) ^ 2 / 2 Then

U = 1

End If

If Y(1) < 0 And Y(2) > 0 And Y(1) >= -Y(2) ^ 2 / 2 Then

U = -1

End If

End Sub

'==============================================================

Sub Uravnen()

' Формирование управления

Upravlen

' Уравнения движения объекта

F(1) = Y(2)

F(2) = U

End Sub

'==============================================================

Sub Runge(x As Single)

x = X0:

For i = 1 To N: Y(i) = Y0(i): Next i: Uravnen

For i = 1 To N: k1(i) = h * F(i): Next i

x = X0 + h / 2

For i = 1 To N: Y(i) = Y0(i) + k1(i) / 2: Next i: Uravnen

For i = 1 To N: k2(i) = h * F(i): Next i

For i = 1 To N: Y(i) = Y0(i) + k2(i) / 2: Next i: Uravnen

For i = 1 To N: k3(i) = h * F(i): Next i

x = X0 + h

For i = 1 To N: Y(i) = Y0(i) + k3(i): Next i: Uravnen

For i = 1 To N: k4(i) = h * F(i): Next i

For i = 1 To N

Y(i) = Y0(i) + (k1(i) + 2 * k2(i) + 2 * k3(i) + k4(i)) / 6

Next i

End Sub

'==============================================================

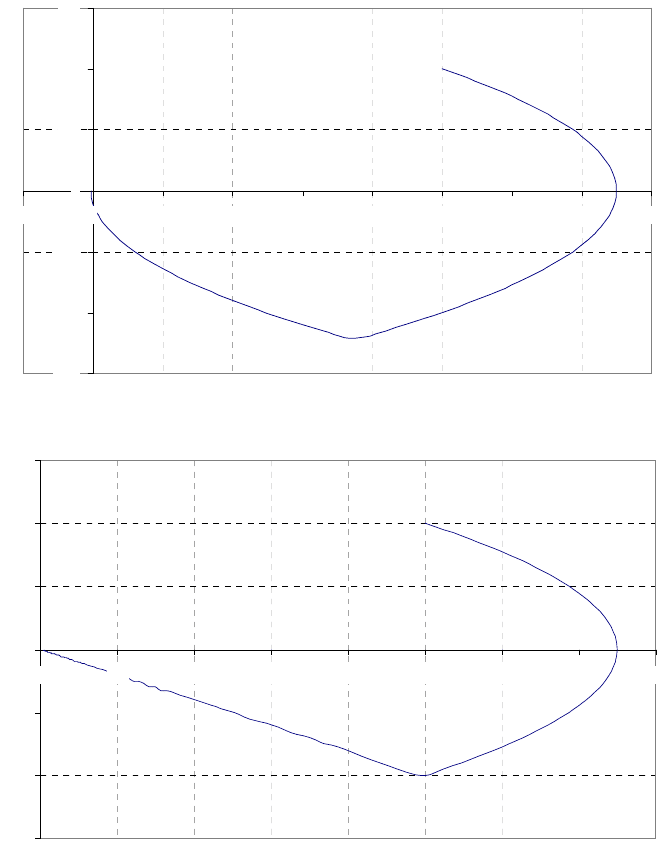
Ниже приведены фазовые портреты при оптимальном и квазиоптимальном вариантах управле-

ния, когда линия переключения (идеально состоящая из двух парабол) аппроксимируется прямой лини-

ей, проходящей через начало координат. Также приведены иллюстрирующие примеры возникновения

«скользящего» режима.

112

-1.5

-1

-0.5

0.5

1.5

-0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

Оптимальная фазовая траектория

-1.5

-1

-0.5

0.5

1.5

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

Квазиоптимальная фазовая траектория при k=-1

113

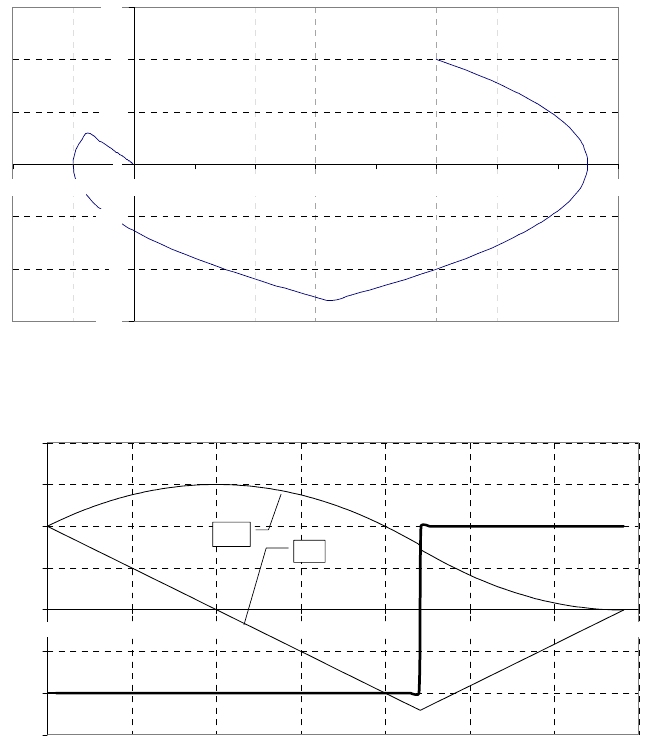
Фазовый портрет при квазиотпимальном управлении

-1.5

-1

-0.5

0.5

1.5

-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

Квазиоптимальная фазовая траектория при k=-2

Изменение фазовых координат и управляющего воздействия

-1.5

-1

-0.5

0.5

1.5

0 0.5 1 1.5 2 2.5 3 3.5

t,C

X1,X2,U

114

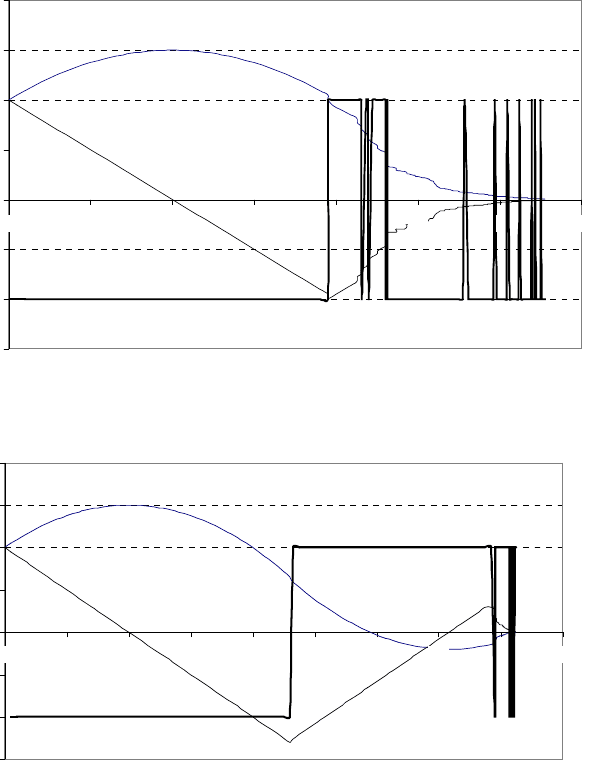
Возникновение скользящего режима

-1.5

-1

-0.5

0.5

1.5

0 0.5 1 1.5 2 2.5 3 3.5

t,C

X1,X2,U

Возникновение скользящего режима

-1.5

-1

-0.5

0.5

1.5

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

t,C

X1,X2,U

Фрагмент текста исходного модуля, определяющего положение исходной точки и параметры ли-

нии переключения:

...

For i = 1 To N

Prom = InputBox("Координата X0(" & Str(i) & ")=", _

" Определение положения начальной точки")

Loop Until IsNumeric(Prom)

Y0(i) = Prom

Next i

Prom = InputBox("Коэффициент наклона линии переключения", _

" Условия возникновения скользящего режима")

Loop Until IsNumeric(Prom)

K = Prom

Фрагмент текста исходного модуля, определяющий поведение объекта при квазиоп-

тимальном управлении:

...

115

'==============================================================

Sub Uravnen()

If Y(2) >= K * Y(1) Then

U = -1

Else

U = 1

End If

F(1) = Y(2)

F(2) = U

End Sub

'==============================================================

13.МАТЕМАТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ

13.1. ПРИНЦИП МАКСИМУМА Л.С.ПОНТРЯГИНА. УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ

Определим некоторые понятия:

1. Множество S точек x=(x

, x

,…, x

) удовлетворяющих соотношению

f(x

, x

,…, x

)=0,

называется

гиперповерхностью пространства X, а упомянутое соотношение уравнением этой ги-

перповерхности. Например, условия

0=Ψαω−Ψ

′

−Ψ

′

+−

svnrur

являются уравнением гиперповерхности.

Если соотношение линейно, т.е. имеет вид

=++++ bxa...xaxa

то гиперповерхность называется

гиперплоскостью.

2. Если функция f имеет первые частные производные по переменным x

, x

,…, x

, то в каждой

точке x определен вектор













∂

,...,

называемый

градиентом функции f(x) и обозначаемый grad f(x).

3. Пусть x

произвольная точка гладкой гиперповерхности. Вектор grad f(x

) называется нор-

мальным вектором

(нормалью) гиперповерхности S в точке x

4. Гиперплоскость, проходящая через точку x

и имеющая вектор grad f(x

) своей нормалью, на-

зывается касательной гиперплоскостью гиперповерхности S в точке x

5. Пусть S

, S

,…, S

– гладкие гиперповерхности, заданные в пространстве X соответственно

уравнениями

, x

,…, x

)=0,

, x

,…, x

)=0,

….

, x

,…, x

)=0.

Пересечение M всех этих гиперповерхностей (т.е. множество всех точек x∈X, удовлетворяющих

всем указанным уравнениям) называется (n-k) мерным

многообразием, если выполнено следующее ус-

ловие: в каждой точке x∈M векторы

grad f

(x), grad f

(x),…, grad f

(x)

линейно независимы. Например, совокупность

116

()











=Ψω−αω+Ψ

′

−Ψ

′

=Ψω−αω−Ψ

′

−Ψ

′

=Ψαω+Ψ

′

−Ψ

′

+−

=Ψαω−Ψ

′

−Ψ

′

+−

.pk

,pk

runsvs

rvnsus

sunrvr

svnrur

определяет многообразие.

Условия трансверсальности. Будем говорить, что вектор ψ(t) (существование которого опре-

делено принципом максимума) удовлетворяет условию трансверсальности в концах траектории x(t), если

он ортогонален всем векторам, лежащим в касательной гиперплоскости конечного или начального мно-

гообразий.

13.2. ПРИНЦИП МАКСИМУМА Л.С.ПОНТРЯГИНА. ЗАДАЧА ПОЗИЦИОНИРОВАНИЯ

АСИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ

Будем полагать, что, как и прежде, реализуется частотный способ управления асинхронным элек-

тродвигателем и поэтому, как и ранее,

необходимо определить связи (определяющие аналитическую

конструкцию оптимального регулятора)

между управляющими воздействиями (относительными зна-

чениями частоты тока статора (α) и напряжения (γ)),

фазовыми координатами, характеризующими

состояние электродвигателя

(потокосцепления, скорость вращения ротора) и его параметрами.

Исходные уравнения движения АД в синхронной системе вращающихся координат U,V образуют

систему дифференциальных связей, описывающих состояние АД

()

()()











ω=

−ΨΨ−ΨΨ=

Ψω−αω−Ψ

′

+Ψ

′

−=

Ψω−αω+Ψ

′

+Ψ

′

−=

Ψαω−Ψ

′

+Ψ

′

−=

Ψαω+Ψ

′

+Ψ

′

−=

−

,McJ

,pk

crvsusvru

runsvs

rvnsus

sunrvr

svnrur

Образуем вспомогательную функцию:

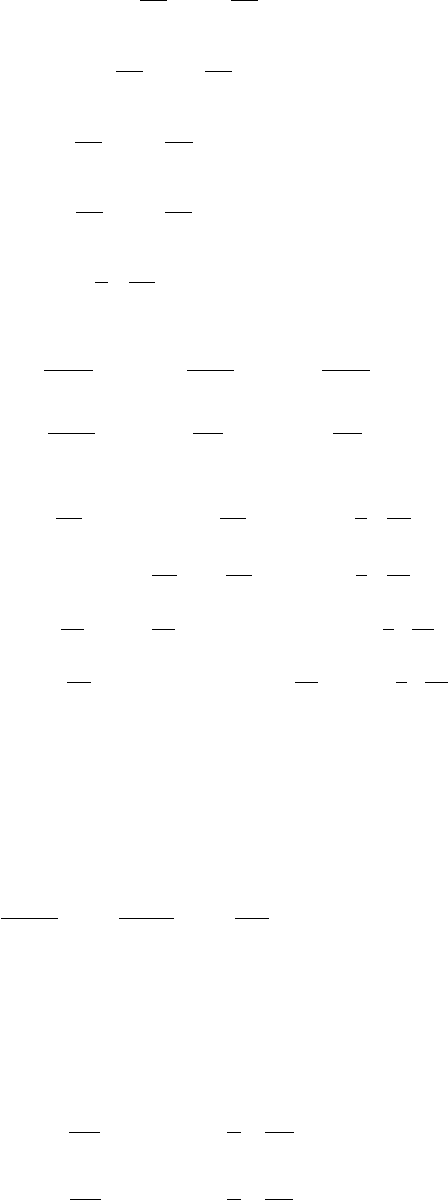
117

()

() ()

()

()()

ωψ+













−ΨΨ−ΨΨ

′

ψ+













Ψω−αω−Ψ

′

+Ψ

′

−ψ+













Ψω−αω+Ψ

′

+Ψ

′

−ψ+













Ψαω−Ψ

′

+Ψ

′

−ψ+













Ψαω+Ψ

′

+Ψ

′

−ψ=

−

pJt

UtH

crvsusvru

runsvs

rvnsus

sunrvr

svnrur

и систему для определения составляющих функции ψ:

rusvsu

γ∂

∂

−=ψ

ω∂

∂

−=ψ

Ψ∂

∂

−=ψ

Ψ∂

∂

−=ψ

Ψ∂

∂

−=ψ

Ψ∂

∂

−=ψ

654

321

&&&

Раскрывая эти связи, будем иметь:

pJk

′

ψ+

′

ψ−αωψ+

′

ψ=ψ

−

53211

pJk

′

ψ−

′

ψ−

′

ψ+αωψ−=ψ

−

54212

()

pJp

′

ψ−ω−αωψ+

′

ψ+

′

ψ−=ψ

−

54313

()

′

ψ+

′

ψ+ω−αωψ−

′

ψ−=ψ

−

54324

,pp

rurv 6435

−Ψψ−Ψψ=ψ

=ψ

Учитывая, что в условиях оптимальности

() () ()()()

(

)()

u,tx,tHmaxtu,tx,tH

ψ=ψ

∈

можем дополнительно записать, полагая непрерывность функций управления

0 0 0 =

α∂

∂

∂ H

откуда следует:

,, 0 0

=ψ=ψ

rur

=Ψψ−Ψψ

С учетом последних выражений, система для определения составляющих функции ψ будет вы-

глядеть:

pJk

′

ψ+

′

ψ−=

−

pJk

′

ψ−

′

ψ−=

−

118

()

pJp

′

ψ−ω−αωψ+

′

ψ+=ψ

−

5433

()

′

ψ+

′

ψ+ω−αωψ−=ψ

−

5434

Ψ−=

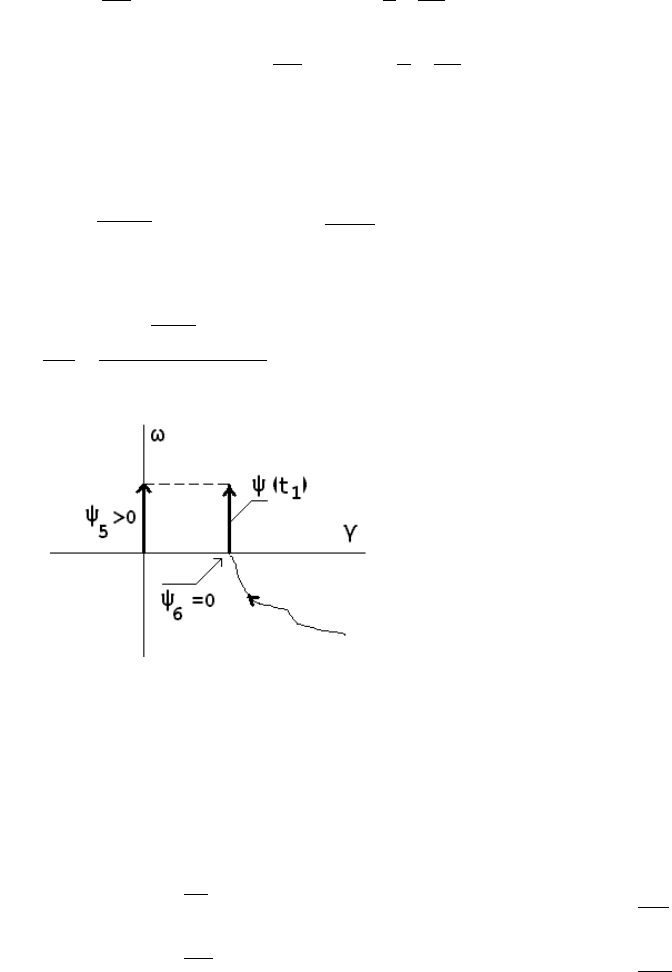
С учетом условий трансверсальности (см. рисунок) решение выглядит так:

Ψψ=ψ

Ψψ−=ψ

=С

, ψ

=0,

где С

=const, а с учетом необходимости выполнения условия H≡1, получим

Ψω













=α

Условия трансверсальности в задаче позиционирования асинхронного электродвигателя

В номинальном режиме работы, при отсутствии необходимости управления С

=J/M. В управляе-

мом варианте эта постоянная определяет сигнал задания.

Продолжим рассмотрение задачи об управлении асинхронным электродвигателем, проводя ана-

логию с задачей об управлении объектом второго порядка.

Основные уравнения движения электропривода можно записать с естественными ограничениями

в виде (для сравнения запишем и уравнения движения объекта 2-го порядка):

АД-

maxmin

MMM

,MJ

∆≤∆≤∆











∆=

ω=

−1

объект 2-го порядка -

≤











где γ - угол поворота вала ротора электродвигателя, ∆M=M-M

– динамический момент. Остальные обо-

значения соответствуют обозначениям, принятым ранее. При этом между обозначениями предыдущей

задачи и рассматриваемой существует связь x

÷γ, x

÷ω, u÷∆M.

Формулировка задачи в прежней постановке, т.е. о переводе объекта (асинхронного электродви-

гателя) из произвольного начального состояния в начало координат физически означает возврат к нуле-

вому значению угла поворота ротора. Этот вариант управления можно представить себе в машинах, у

которых по условиям выполнения технологического процесса исполнительный орган должен вернуться в

исходное положение.

Запишем вспомогательную функцию

119

MH ∆ψ+ωψ=

21 .

Для вспомогательных переменных ψ, как и прежде, получаем систему уравнений

121

0 ψ−=ψ=ψ

Также находим: ψ

; ψ

= -d

t+d

, где d

, d

– постоянные интегрирования.

В силу соотношения максимума (D) пишем

() ()

.tif,MtM

;tif,MtM

min

max

<ψ∆=∆

>ψ∆=∆

Отсюда

теоретически следует, что каждое оптимальное управление является функцией, прини-

мающей значения ∆M

max

,, ∆M

min

и имеющей не более двух интервалов постоянства.

Рассмотрим фазовые траектории, соответствующие возможным вариантам движений АД. Как и

ранее, можно записать

∆

откуда следует при условии, что ∆M=const:

()

+ω

∆

=γ

Рассмотрим возможность обеспечения условия ∆M=const. Условия получения оптимального, в

смысле быстродействия, управления требуют, чтобы динамический момент АД при изменении знака со-

ставляющей ψ

(t) изменял свое значение от минимально возможного значения до максимально возмож-

ного. Конечно, такая возможность имеется, например, при реализации торможения АД противовключе-

нием. Заметим, что при этом динамический момент не является постоянной величиной, а функции

управляющего параметра принимает на себя электрическая частота вращения поля статора - ω

эл

=αω

. В

такой постановке появляется управляющий параметр α, который может принимать значения α=±1. Ко-

нечно, следует ожидать при этом появления скользящих режимов, которые нежелательны, но мы пока

рассматриваем

потенциальные возможности управления.

Анализ возможных оптимальных движений АД в исходное положение показывает, что они

должны формироваться по следующим правилам:

-при нахождении АД в I-м квадранте фазовой плоскости γ,ω:

If γ > 0 And ω > 0 Then α = -1

-при нахождении АД во II-м квадранте:

If γ < 0 And ω > 0 And γ < - ω

(J/2∆M) Then α = 1

If γ < 0 And ω > 0 And γ >= - ω

(J/2∆M) Then α = -1

-при нахождении АД в III-м квадранте:

If γ < 0 And ω < 0 Then α = 1

-при нахождении АД в IV-м квадранте:

If γ > 0 And ω < 0 And γ > ω

(J/2∆M) Then α = -1

If γ > 0 And ω < 0 And γ <= ω

(J/2∆M) Then α = 1

При этом фазовая траектория может выглядеть, например, следующим образом:

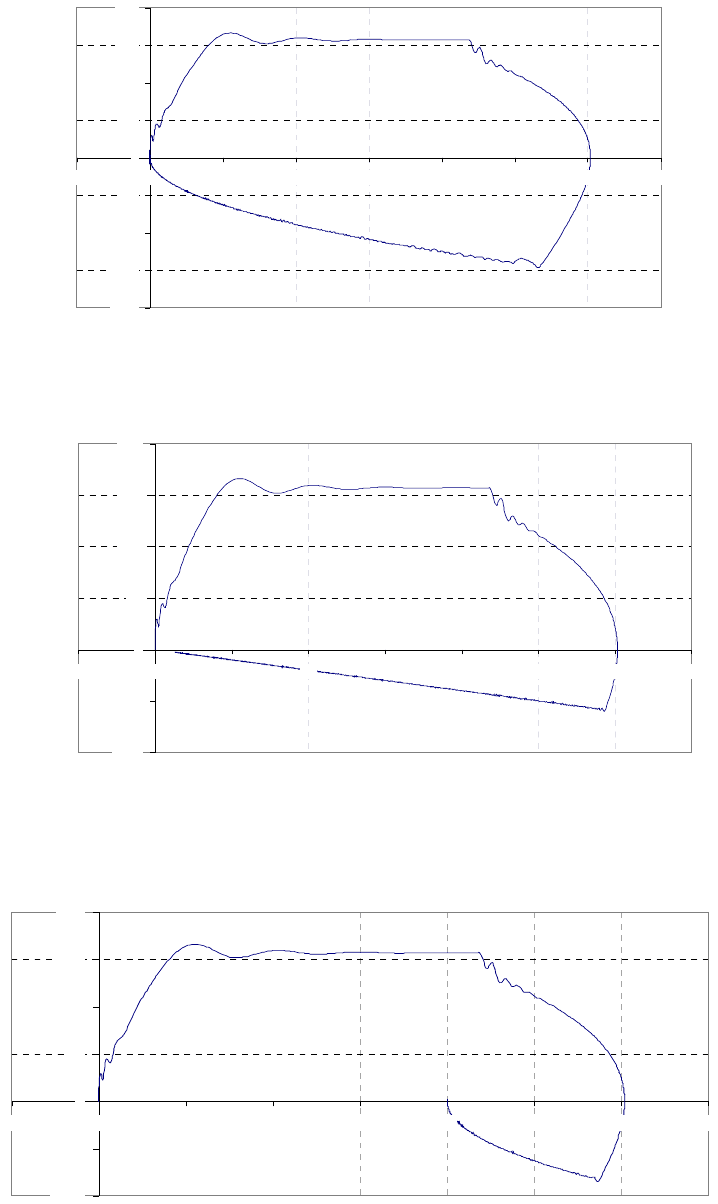
120

Позиционирование АД

-200

-150

-100

-50

100

150

200

-10 0 10 20 30 40 50 60 70

Угол поворота ротора, рад

Скорость вращения,1/С

Если реализуется линия переключения γ

= -Kω, то процесс перехода выглядит так:

Позиционирование АД

-100

-50

100

150

200

-10 0 10 20 30 40 50 60 70

Угол поворота ротора, рад

Скорость вращения,1/С

При реализации γ

=А±ω

(J/2∆M) процесс позиционирования представлен на следующем ри-

сунке:

Позиционирование АД

-100

-50

100

150

200

-10 0 10 20 30 40 50 60 70

Угол по ворота ротора, рад

Скорость вращения,1/С