Ещин Е.К. Моделирование систем управления электромеханическими объектами

101

Next i

Y0(9) = 0.0001: Y(10) = 0.0001

'=========================================================

Tvn = 0.3 ' Время подачи пульсирующей нагрузки на вал АД

Tvu = 0.6 ' Время включения управления состоянием АД

'=========================================================

b1 = 1000: b2 = 1500

' Параметры для двигателей ВРП160М4

Rs1 = 0.516: Rr1 = 0.406

Xs1 = 1.419: Xr1 = 1.1

Xm1 = 35: p1 = 2

GD21 = 0.7

Rs2 = 0.516: Rr2 = 0.606

Xs2 = 1.419: Xr2 = 1.2

Xm2 = 36: p2 = 2

GD22 = 0.7

' Коэффициенты для уравнений движения АД

l11 = Xs1 / 314

l21 = Xr1 / 314

lm1 = Xm1 / 314

lps1 = l11 + l21 * lm1 / (l21 + lm1)

lpr1 = l21 + l11 * lm1 / (l11 + lm1)

ks1 = lm1 / (lm1 + l11)

kr1 = lm1 / (lm1 + l21)

c1 = 3 * p1 * ks1 / (2 * lpr1)

l12 = Xs2 / 314

l22 = Xr2 / 314

lm2 = Xm2 / 314

lps2 = l12 + l22 * lm2 / (l22 + lm2)

lpr2 = l22 + l12 * lm2 / (l12 + lm2)

ks2 = lm2 / (lm2 + l12)

kr2 = lm2 / (lm2 + l22)

c2 = 3 * p2 * ks2 / (2 * lpr2)

Shet ' Основная обработка и подготовка данных

MsgBox "Все!"

End Sub

'===========================================================

Sub Shet()

Dim L, K As Integer

Worksheets("Лист3").Select

Worksheets("Лист3").Range("A1: M1000").Clear

j = 2

With Worksheets("Лист3")

For K = 1 To N

.Cells(1, K + 1) = Y0(K)

Next K

End With

x = X0

While x <= Xk

Runge (x)

For i = 1 To N: Yz(i) = Y(i): Next i

102

h = h / 2

Runge (x)

For i = 1 To N: Y0(i) = Y(i): Next i

x = x + h

Runge (x)

L = 0

For i = 1 To N

If Abs(Yz(i) - Y(i)) < eps * Abs(Yz(i)) Then

L = L + 1

End If

Next i

If L = N Then

With Worksheets("Лист3")

For K = 1 To N

.Cells(j, K + 1) = Y(K)

Y0(K) = Y(K)

Y0z(K) = Y(K)

Next K

.Cells(j, 1) = x

.Cells(j, 15) = c1 * (Y(3) * Y(2) - Y(1) * Y(4))

.Cells(j, 16) = c1 * (Y(7) * Y(6) - Y(5) * Y(8))

End With

x = x + h

h = Hz

j = j + 1

Else

x = x - h

End If

Wend

End Sub

'===========================================================

Sub Uravnen()

' Формирование момента сопротивления

If x <= Tvn Then

Mc = 0

Else

Mc = 500 + 200 * Sin(6.28 * 10 * x) + 100 * Sin(6.28 * 5 * x)

End If

' Формирование управляющего воздействия

If x <= Tvu Then

alfa1 = 1

alfa2 = 1

Else

alfa2 = 1.05 * p2 * Y(10) / 314

alfa1 = p1 * Y(9) / 314 + (alfa2 - p2 * Y(10) / 314) * (Rr1 / Rr2) *

((Y(7) ^ 2 + Y(8) ^ 2) / (Y(3) ^ 2 + Y(4) ^ 2))

End If

' 1-й двигатель

F(1) = 537 * alfa1 - Rs1 / lps1 * Y(1) + Rs1 / lps1 * kr1 * Y(3) + 314 *

alfa1 * Y(2)

F(2) = -Rs1 / lps1 * Y(2) + Rs1 / lps1 * kr1 * Y(4) - 314 * alfa1 * Y(1)

F(3) = -Rr1 / lpr1 * Y(3) + Rr1 / lpr1 * ks1 * Y(1) + (314 * alfa1 - p1 *

Y(9)) * Y(4)

F(4) = -Rr1 / lpr1 * Y(4) + Rr1 / lpr1 * ks1 * Y(2) - (314 * alfa1 - p1 *

Y(9)) * Y(3)

' 2-й двигатель

F(5) = 537 - Rs2 / lps2 * Y(5) + Rs2 / lps2 * kr2 * Y(7) + 314 * alfa2 * Y(6)

103

F(6) = -Rs2 / lps2 * Y(6) + Rs2 / lps2 * kr2 * Y(8) - 314 * alfa2 * Y(5)

F(7) = -Rr2 / lpr2 * Y(7) + Rr2 / lpr2 * ks2 * Y(5) + (314 * alfa2 - p2 *

Y(10)) * Y(8)

F(8) = -Rr2 / lpr2 * Y(8) + Rr2 / lpr2 * ks2 * Y(6) - (314 * alfa2 - p2 *

Y(10)) * Y(7)

' Скорости 1-го и 2-го двигателей соответственно Y(9), Y(10)

F(9) = 4 * (c1 * (Y(3) * Y(2) - Y(1) * Y(4)) - Y(11)) / GD21

F(10) = 4 * (c2 * (Y(7) * Y(6) - Y(5) * Y(8)) - Y(12)) / GD22

' Упругие моменты в трансмиссиях Y(11), Y(12)

F(11) = b1 * (Y(9) - Y(13))

F(12) = b2 * (Y(10) - Y(13))

' Скорость вращения испонительного органа Y(13)

F(13) = 4 * (Y(11) + Y(12) - Mc) / (GD21 + GD22)

End Sub

'===========================================================

Sub Runge(x As Single)

x = X0

For i = 1 To N: Y(i) = Y0(i): Next i: Uravnen

For i = 1 To N: k1(i) = h * F(i): Next i

x = X0 + h / 2

For i = 1 To N: Y(i) = Y0(i) + k1(i) / 2: Next i: Uravnen

For i = 1 To N: k2(i) = h * F(i): Next i

For i = 1 To N: Y(i) = Y0(i) + k2(i) / 2: Next i: Uravnen

For i = 1 To N: k3(i) = h * F(i): Next i

x = X0 + h

For i = 1 To N: Y(i) = Y0(i) + k3(i): Next i: Uravnen

For i = 1 To N: k4(i) = h * F(i): Next i

For i = 1 To N

Y(i) = Y0(i) + (k1(i) + 2 * k2(i) + 2 * k3(i) + k4(i)) / 6

Next i

End Sub

'===========================================================

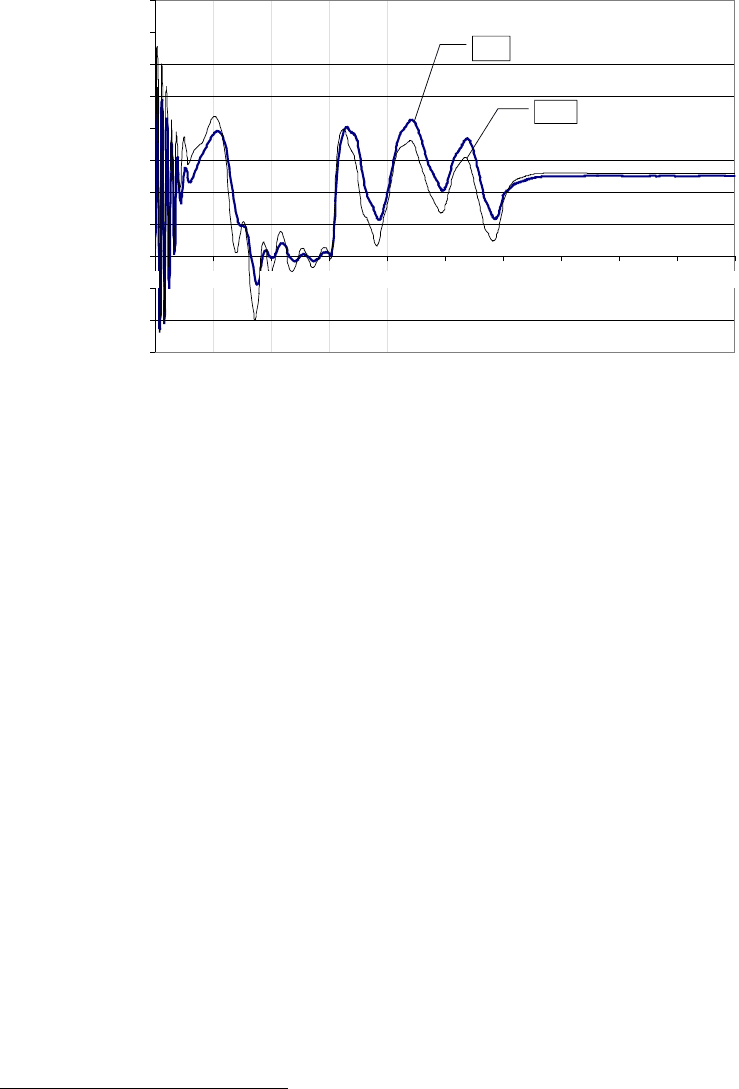
Ниже приведены результаты моделирования совместного управления при реализации оптималь-

ного управлении «ведущим» двигателем.

104

-300

-200

-100

0

100

200

300

400

500

600

700

800

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

t,C

M,Hm

M1

M2

12.МАТЕМАТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ

12.1.ПРИНЦИП МАКСИМУМА Л.С.ПОНТРЯГИНА

61

. ЗАДАЧА ОПТИМАЛЬНОГО БЫСТРОДЕЙСТВИЯ

Примем следующее математическое описание управляемого объекта. Состояние объекта задается

(в каждый момент времени) n числами x

1

, x

2

,…, x

n

, которые называются фазовыми координатами объек-

та. Движение объекта заключается с математической точки зрения в том, что его состояние с течением

времени изменяется, т.е. x

1

, x

2

,…, x

n

являются переменными величинами (функциями времени). Движе-

ние объекта происходит не самопроизвольно, им можно управлять; для этого объект снабжен «рулями»,

положение которых характеризуется (в каждый момент времени) r числами u

1

,u

2

,…,u

r

; эти числа назы-

ваются управляющими параметрами.

Величины u

1

, u

2

,…, u

r

удобно считать координатами некоторого вектора u=( u

1

,u

2

,…,u

r

), также на-

зываемого управляющим параметром. Точно также величины x

1

, x

2

,…, x

n

удобно рассматривать как ко-

ординаты некоторого вектора (или точки) x=( x

1

, x

2

,…, x

n

) в n-мерном пространстве с координатами x

1

,

x

2

,…, x

n

. Эту точку называют фазовым состоянием объекта, а пространство, в котором в виде точек изо-

бражаются фазовые состояния, называется фазовым пространством рассматриваемого объекта.

Чтобы полностью задать движение объекта, нужно задать его фазовое состояние x

0

=( x

1

0

, x

2

0

,…,

x

n

0

) в начальный момент времени t

0

и выбрать управляющие функции u

1

(t),u

2

(t),…,u

r

(t), определяющие

вектор-функцию u(t) =(u

1

(t),u

2

(t),…,u

r

(t)). Эту функцию называют управлением.

Закон движения объекта описывается дифференциальными уравнениями. Чаще всего эти уравне-

ния дают выражения производных от фазовых координат через сами фазовые координаты и управляю-

щие параметры, т.е. имеют вид

61

Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория опти-

мальных процессов. М.: Наука, 1976. –392 с.

Болтянский В.Г. Математические методы оптимального управления. -М.: Наука,1969. -351 c.

(Изложение материала по В.Г.Болтянскому без некоторых особенностей математического характера

(например, требования дифференцируемости некоторой функции

ω

(x) и пр.), которые м.б. при первом

знакомстве с проблемой и не очень существенны для студентов-электриков)

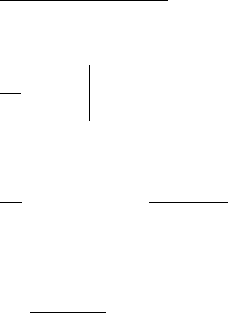
105

(

)

()











=

,u,...,u,u,x,..,x,xfx

....,..................................................

,u,...,u,u,x,..,x,xfx

rnnn

rn

2121

212122

212111

&

где f

1

,f

2

,…,f

n

некоторые функции, определяемые внутренним устройством объекта.

Естественно также считать, что управляющие параметры u

1

, u

2

,…, u

r

не могут принимать совер-

шенно произвольные значения, а подчинены некоторым ограничениям.

Рассмотрим задачу об оптимальном переходе – в смысле быстродействия – из фазового со-

стояния x в фазовое состояние x

1

. При этом конечную точку будем считать фиксированной, а в качест-

ве начальной точки будем рассматривать различные точки фазового пространства.

Будем предполагать, что для рассматриваемого управляемого объекта выполняется следующая

ГИПОТЕЗА – какова бы ни была отличная от x

1

точка x фазового пространства, существует оптималь-

ный (в смысле быстродействия) процесс перехода из точки x в точку x

1

.

Время, в течение которого осуществляется оптимальный переход из начальной точки в конечную

точку, обозначим через T(x). Иначе говоря, за время меньшее, чем T(x) перейти из точки x в точку x

1

не-

возможно.

В дальнейших рассуждениях будет удобно вместо T(x) ввести функцию ω(x), отличающуюся от

нее знаком:

() ()

xTx −=ω

. (12.1)

Пусть x

0

– произвольная, отличная от x

1

точка фазового пространства, а u

0

- произвольная точка

области управления U. Предположим, что объект находится в начальный момент времени t

0

в фазовом

состоянии x

0

и движется в течении некоторого времени под воздействием постоянного управления u=u

0

.

Фазовую траекторию при этом движении обозначим через

(

)

(

)

(

)()

(

)

ty,...,ty,tyty

n21

=

.

Если мы будем двигаться из точки x

0

до точки y(t) по рассматриваемой траектории, то затратим

на это движение время t-t

0

. Двигаясь затем из точки y(t) оптимально мы затратим на движение от точки

y(t) до точки x

1

время T(y(t)). В результате мы совершим переход из точки x

0

в точку x

1

, затратив на этот

переход время (t-t

0

)+ T(y(t)).

Но так как оптимальное время движения от точки x

0

до точки x

1

равно T(x

0

)), т.е.равно T(y(t

0

)), то

T(y(t

0

))≤ (t-t

0

)+ T(y(t)).

Заменяя функцию T через ω и разделив обе части неравенства на положительную величи-

ну t-t

0

, получаем отсюда

()() ()()

1

0

≤

−

ω−ω

tt

tyty

и поэтому, переходя к пределу при t

→

t

0

, находим

()()

1

0

при

≤ω

=tt

ty

dt

d

. (12.2)

Производная в левой части выражения (12.2) вычисляется по формуле полной производной

()()

()

ty

x

ty

dt

d

i

n

i

&

∑

=

∂

ω∂

=ω

1

.

Поэтому (12.2) можно записать в виде

()()

()

1

00

1

≤

∂

ω∂

∑

=

u,xf

x

ty

i

n

i

.

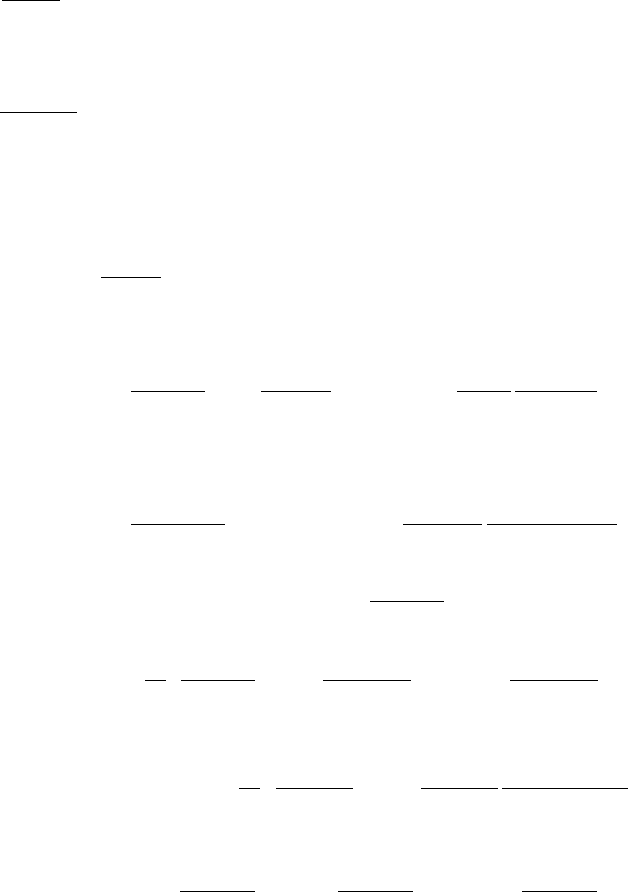
106

Исходное положение объекта и управление были заданы произвольно. Таким образом, для любой

(отличной от конечной) точки фазового пространства и любой точки и области управления выполнено

соотношение

()

1

≤

∂

ω∂

∑

=

u,xf

x

i

n

i

. (12.3)

Если же процесс оптимален, то имеет место

()()

() ()()

1

=

∂

ω∂

∑

=

tu,txf

x

tx

i

n

i

, (12.4)

т.е. для каждого оптимального процесса в течение всего времени движения выполняется равенст-

во (12.4).

Введем в рассмотрение функцию

()

u,xf

x

u,xB

i

n

i

∑

=

∂

ω∂

=

1

и запишем ее частные производные по фазовым координатам для

оптимального процесса

() ()

()

.n,...,,k,

x

u,xf

x

u,xf

xx

x

u,xB

k

i

n

i

n

i

kik

21

11

2

=

∂

ω∂

+

∂∂

ω∂

=

∂

∑∑

=

Из (12.4) следует, что функция B(x,u(t)) достигает при оптимальном управлении максимума и по-

этому ее частные производные по фазовым координатам обращаются в нуль.

()()

() ()()

()()

() ()()

.n,...,,k,

x

tu,txf

x

tx

tu,txf

xx

tx

k

i

n

i

n

i

ki

21 0

11

2

==

∂

ω∂

+

∂∂

ω∂

∑∑

=

(12.5)

Дополнительно дифференцируя функцию

(

)

(

)

k

x

tx

∂

ω

∂

по времени, находим

()() ()()

()

()()

() ()()

.tu,txf

xx

tx

xx

tx

x

tx

dt

d

i

n

i

ik

i

n

i

ikk

∑∑

=

∂∂

ω∂

=

∂∂

ω∂

=













∂

ω∂

1

2

1

2

&

Поэтому соотношение (12.5) может быть переписано в виде

()() ()() () ()()

.n,...,,k,

x

tu,txf

x

tx

x

tx

dt

d

k

i

n

i

ik

21 0

1

==

∂

ω∂

+













∂

ω∂

∑

=

(12.6)

Введем следующие обозначения

()()

()

(

)

(

)

()

(

)

(

)

()

.t

x

tx

,...,t

x

tx

,t

x

tx

n

ψ=

∂

ω

∂

ψ=

∂

ω

∂

ψ=

∂

ω∂

2

1

Тогда функция B запишется таким образом

() ()( ) () () ()()

∑

=

ψ=

n

i

tu,txfttu,txB

1

,

и соотношение (12.4) принимает вид

() () ()()

1

≡ψ

∑

=

n

i

tu,txft

(12.7)

для оптимального процесса

()

(

)()

10

ttt,tx,tu

≤

.

107

Соотношения (12.6) можно записать следующим образом

() ()

() ()()

.n,...,,k,

x

tu,txf

tt

dt

d

k

i

n

i

ik

21 0

1

==

∂

ψ+ψ

∑

=

(12.8)

Введем в рассмотрение следующую функцию

( ) () () () ()

u,xf...u,xfu,xfu,xfu,x,H

n

i

2

1

ψ++ψ+ψ=ψ=ψ

∑

=

и далее сформулируем следующую теорему, которая носит название

принципа максимума:

Предположим, что для рассматриваемого управляемого объекта, описываемого уравнением

движения

(

)

Uu,u,xfx

∈

=

&

(А)

и предписанного конечного состояния выполнена высказанная выше гипотеза. Пусть

() ()()

10

ttt,tx,tu ≤≤

- некоторый оптимальный процесс, переводящий объект из начального состояния

x

0

в состояние x

1

. Введем в рассмотрение функцию H, зависящую от переменных x

1

, x

2

,…, x

n

, u

1

, u

2

,…, u

r

и

некоторых вспомогательных переменных

ψ

1

,…,

ψ

n

() ()

∑

=

ψ=ψ

n

i

u,xfu,x,H

1

. (B)

С помощью этой функции H запишем следующую систему дифференциальных уравнений для

вспомогательных переменных:

(

)

(

)

(

)

.n,...,,k,

x

tu,tx,H

k

21 =

∂

ψ

∂

−=ψ

&

(С)

Тогда, если процесс

() ()()

10

ttt,tx,tu

≤

является оптимальным, то существует такое нетри-

виальное решение

() () ()()

t,...,tt

n

ψψ=ψ

1

системы (С), что для любого момента времени выполнено

условие

максимума

(

)

(

)

(

)

(

)

(

)()

(

)

u,tx,tHmaxtu,tx,tH

Uu

ψ

=

ψ

∈

(D)

и условие

() () ()()

1=ψ tu,tx,tH

.

12.2.ПРИМЕР. УПРАВЛЕНИЕ ОБЪЕКТОМ ВТОРОГО ПОРЯДКА

Рассмотрим объект с уравнениями движения

11

2

21

≤≤











=

u

;ux

,xx

&

Для этого объекта рассмотрим задачу о быстрейшем попадании в начало координат (0, 0) из за-

данного начального состояния x

0

=(x

1

0

,x

2

0

).

Функция H запишется

uxH

2

1

ψ+ψ=

.

Для вспомогательных переменных получаем систему уравнений

121

0 ψ−=ψ=ψ

&&

,

.

108

Из этой системы следует ψ

1

=d

1

; ψ

2

= -d

1

t+d

2

, где d

1

, d

2

– постоянные интегрирования.

В силу соотношения максимума (D) находим

() ()

.tif,tu

;tif,tu

0 1

2

<ψ−=

>ψ+=

Отсюда следует, что каждое оптимальное управление является кусочно-постоянной функцией,

принимающей значения ±1 и имеющей не более двух интервалов постоянства.

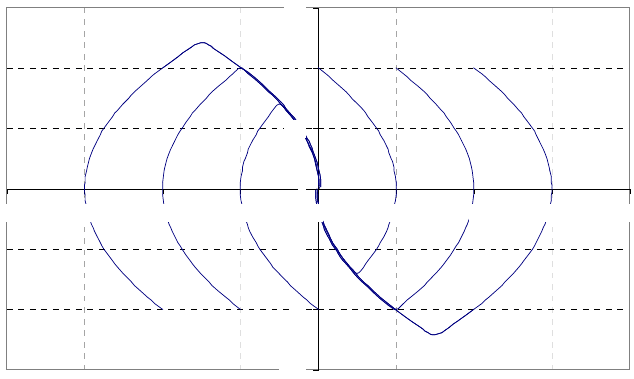
Семейства фазовых траекторий, соответствующие возможным вариантам движений объекта в

начало координат представлены на рисунке ниже. Каждый из участков траекторий представляет собой

дугу параболы. В самом деле, для отрезка времени, когда u

≡

1 с использованием уравнений движения

можно получить

2

1

x

dx

=

,

откуда следует

()

cxx +=

2

21

2

1

.

Для отрезков времени, когда u

≡

-1, аналогичным образом получим

()

cxx +−=

2

21

2

1

.

Анализ возможных оптимальных движений объекта в начало координат показывает, что

они должны формироваться по следующим правилам:

-при нахождении объекта в I-м квадранте

If x

1

> 0 And x

2

> 0 Then U = -1

-при нахождении объекта во II-м квадранте

If x

1

< 0 And x

2

> 0 And x

1

< - (x

2

)

2

/ 2 Then U = 1

If x

1

< 0 And x

2

> 0 And x

1

>= - (x

2

)

2

/ 2 Then U = -1

-при нахождении объекта в III-м квадранте

If x

1

< 0 And x

2

< 0 Then U = 1

-при нахождении объекта в IV-м квадранте

If x

1

> 0 And x

2

< 0 And x

1

> (x

2

)

2

/ 2 Then U = -1

If x

1

> 0 And x

2

< 0 And x

1

<= (x

2

)

2

/ 2 Then U = 1

Эта совокупность определяет синтезирующую функцию u=u(x), а знание синтезирующей функ-

ции позволяет считать задачу управления решенной математически до конца

62

.

62

Болтянский В.Г. Математические методы оптимального управления. -М.: Наука,1969. -351 c.

109

-1.5

-1

-0.5

0

0.5

1

1.5

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2

x1

x2

Оптимальные фазовые траектории

Далее приведен текст исходного модуля на Visual Basic для среды Excel, реализующего рассмот-

ренную задачу оптимального управления объектом второго порядка:

' Учебные задачи кафедры ВТ

' Семейство оптимальных траекторий

'=============================================================

' Понтрягин Л.С.,Болтянский В.Г.,Гамкрелидзе Р.В.,Мищенко Е.Ф.

' Математическая теория оптимальных процессов .-4-е изд.

' -М.: Наука,1983. -392 c.

'==============================================================

Option Explicit

Public j, N, i As Integer

Public Y0(), Y0I(), Yz(), Y0z(), _

Y(), F(), _

k1(), k2(), _

k3(), k4() As Single

Public x, X0z, X0, _

Xk, h, Hz, _

eps, K, U, x1, x2 As Single

'==============================================================

Sub Pontrjagin()

Dim Prom As Single

Dim Mess As String

N = 2

ReDim Y0(N), Y0I(N), Yz(N), Y0z(N), _

Y(N), F(N), _

k1(N), k2(N), k3(N), k4(N)

Mess = MsgBox("Построение семейства оптимальных траекторий", , _

" Учебные задачи кафедры ВТ (Ещин Е.К.)")

eps = 0.000001: h = 0.05: Hz = h

X0 = 0: X0z = X0: h = Hz: Xk = 5

Worksheets("Лист2").Select

Worksheets("Лист2").Range("A1: E1000").Clear

j = 2

' Определение начальных точек и движение из них в начало координат

For x2 = -1 To 1 Step 2

110

For x1 = -1 To 1 Step 0.5

Y0(1) = x1: Y0(2) = x2

Shet

j = j + 1

Next x1

Next x2

End Sub

'==============================================================

Sub Shet()

Dim L, K As Integer

With Worksheets("Лист2")

For K = 1 To N

.Cells(j, K + 1) = Y0(K)

Y(K) = Y0(K)

Next K

.Cells(j, 1) = X0 ' Запись времени

Upravlen

.Cells(j, 4) = U

End With

j = j + 1

x = X0

While (Y0(1) ^ 2 + Y0(2) ^ 2) > 0.001

Runge (x)

For i = 1 To N: Yz(i) = Y(i): Next i

h = h / 2

Runge (x)

For i = 1 To N: Y0(i) = Y(i): Next i

x = x + h

Runge (x)

L = 0

For i = 1 To N

If Abs(Yz(i) - Y(i)) < eps * Abs(Yz(i)) Then

L = L + 1

End If

Next i

If L = N Then

With Worksheets("Лист2")

For K = 1 To N

.Cells(j, K + 1) = Y(K)

Y0(K) = Y(K)

Y0z(K) = Y(K)

Next K

.Cells(j, 1) = x + h ' Запись времени

.Cells(j, 4) = U ' Запись управления

End With

x = x + h

h = Hz

j = j + 1

Else

x = x - h

End If

Wend

End Sub

'==============================================================

Sub Upravlen()

' Определение нахождения фазовой точки и формирование управления

If Y(1) > 0 And Y(2) > 0 Then

Ещин Е.К. Моделирование систем управления электромеханическими объектами

Подождите немного. Документ загружается.