Ещин Е.К. Моделирование систем управления электромеханическими объектами
Подождите немного. Документ загружается.

71
8.3.ВАРИАЦИЯ
Дадим некоторые определения.
1.Приращением или вариацией аргумента функционала v[y(x)] называется разность между двумя
функциями δy=y(x)-y
1
(x). При этом предполагается, что y(x) меняется произвольно в некотором классе
функций.
2.Функционал v[y(x)] называется непрерывным, если малому изменению y(x) соответствует малое
изменение функционала.
3.Линейным функционалом называется функционал L[y(x)] удовлетворяющий следующим усло-
виям:
()
[]
()
[]
xycLxcyL =
,
где c – произвольная постоянная и
() ()
[]
()
[]
(
)
[]
xyLxyLxyxyL
2121
+=+
.
4.Если приращение функционала
()
[]
()
[]
xyvyxyvv −δ+=∆
можно представить в виде
(
)
[
]
(
)
(
)
ymaxy,xyy,xyLv
δ
δ
β
+
δ
=∆
, где L[y(x),δy] – линейный по от-
ношению к δy функционал, max|δy| - максимальное значение δy и
(
)
(
)
0→
δ
β
y,xy
при max|δy|→0, то ли-
нейная по отношению к δy часть приращения функционала называется вариацией функционала и обо-
значается δv.
Таким образом,
вариация функционала – это главная, линейная по отношению к приращению
функции часть приращения функционала.
Если функционал имеет вариацию в смысле главной линейной части приращения, то его
приращение можно записать в виде
()
[]
()
[]
xyvyxyvv −αδ+=∆
где α- варьируемая переменная, а y(x) и δy фиксированы.
Последнее выражение можно также записать в виде
()
[]
()()
ymaxy,xyy,xyLv
α
δαδβ+αδ=∆
.
Производная от v[y(x)+αδy] по α при α=0
()
[]
(
)
(
)
=
α
α
δ
α
δ
β
+
αδ
=
α
∆
=
α∆
∆
→α→α→α∆
ymaxy,xyy,xyL
lim
v
lim
v
lim
000
()
[]
()()
()
[]
y,xyL
ymaxy,xy
lim
y,xyL
lim δ=
α
δ
α
αδ
β
+
α
αδ
=
→α→α 00
, так как
(
)
(
)
0→αδ
β
y,xy
при α→0.
Таким образом, вариация функционала v[y(x)] равна
()
[]
0=α
αδ+
α∂
∂
yxyv
Если функционал v[y(x)], имеющий вариацию, достигает максимума или минимума при
у=у
0
(x), то δv =0.
В самом деле, при фиксированных y
0
(x) и δy v[y
0
(x)+α δy]=ϕ(α) является функцией α, которая при
α=0, по предположению достигает максимума или минимума, следовательно,
()
[]
0
0
0
=αδ+
α∂
∂
=
α
yxyv
,
т.е. δv =0.
72
8.4.УРАВНЕНИЕ ЭЙЛЕРА
48
Исследуем на экстремум функционал
()
[]
() ()()
,dxxy,xy,xFxyv
x
x
o
∫
′
=
1
причем граничные точки допустимых кривых закреплены y(x
o
)=y
o
и y(x
1
)=y
1
.
Необходимым условием экстремума, как было выше показано, является обращение в нуль вариа-
ции функционала.
Возьмем какую-нибудь близкую к y=y(x) допустимую функцию
)x(yy
=
и образуем при их по-
мощи однопараметрическое семейство функций
()() () ()
()
xyxyxy,xy −α+=α
.
Если рассматривать значения функционала только на этом однопараметрическом семействе, то
функционал превращается в функцию α:
() ()()()
dx,xy,,xy,xF
x
x
x
∫
α
′
α=αϕ
1
0
.
Необходимым условием экстремума этой функции является обращение в нуль ее производной
при α=0. Эта производная записывается в виде
() () ()
dx,xyF,xyF
x
x
yy
∫
α
′
α∂
∂
+α
α∂
∂
=αϕ
′
′
1
0
,
где
()()()
α
′
α
∂
∂
= ,xy,,xy,xF
y
F
xy
,
()()()
α
′
α
′
∂
∂
=
′
,xy,,xy,xF
y
F
xy
.
Так как
() ()
[]
yyxy,xy δ=αδ+
α∂
∂
=α
α∂
∂
и
() ()
[]
yyxy,xy
′
δ=δ
′
α+
′
α∂
∂
=α
′
α∂
∂
,
получим
() ()()( ) ()()()
[]
dxy,xy,,xy,xFy,xy,,xy,xF
x
x
xyxy
∫
′
δα
′
α+δα
′
α=αϕ
′
′
1
0
.
() () ()()()()()
[]
dxyxy,xy,xFyxy,xy,xF
x
x
xyxy
∫
′
δ
′
+δ
′
=ϕ
′
′
1
0
0
.
Ранее было установлено, что
()
0
ϕ
′
называется вариацией функционала и обозначается
δ
v. Необ-
ходимое условие экстремума функционала заключается в обращении в нуль его вариации:
δ
v=0. Для
функционала
48
Leonhard Euler was born at Bâle on April 15, 1707, and died at St. Petersburg on September 7, 1783
73
()
[]
() ()
()
dxxy,xy,xFxyv
x
x
,
o
∫
=
1
это условие имеет вид
(8.1)
[]
.dxyFyF
x
x
yy
0
1
0
=
′
δ+δ
∫
′
Интегрируем второе слагаемое по частям. Запишем последовательно
()
ydFydx
dx
d
FdxyF
yyy
δ=δ=
′
δ
∫∫∫
′′′
.
Пусть
()
yddv,Fu
y
δ==
′
, тогда
∫∫
′′′
δ−δ=
′
δ
1
1
1
x
x
y
x
x
y
x
x
y
o
o
o
dxF
dx
d
yyFdxyF
и условие (8.1) запишется
0
1
1
=δ
−+δ
∫
′′
x
x
yy
x
x
y
o
o
ydxF
dx
d
FyF
.
Так как
0
0
=δ
x
y
и
0
1
=δ
x
y
, то с учетом основной леммы вариационного исчисления
49
полу-
чим уравнение Эйлера
0=−
′
yy
F
dx
d
F
,
которое можно записать также в виде
0=−
′′
−
′
−
′′′′
xyyyyyy
FyFyFF
,
где
xy
F
F,
y
F
F,
yy
F
F,
y
F
F
xyyyyyy
∂
′
∂
∂
=
′
∂
∂
=
∂
′
∂
∂
=
∂
∂
=
′′′′
2
2
22
.
Рассмотрим простейший пример.
Значение величины электромагнитных потерь в асинхронном электродвигателе можно выразить
следующим образом
50
dtBAv
t
t
∫
µ
β
+β=
1
0
1
,
где
A=(k
1
+k
2
α
), B=(k
3
+k
4
α
), β - абсолютное скольжение, β=α-α
р
, µ=(γ/α)
2
β.
С учетом последнего преобразуем исходный функционал к виду
49
Основная лемма вариационного исчисления звучит так - если для каждой непрерывной функции
η
(x) ,
где функция Ф(
x) непрерывна на отрезке [x
o
,x
1
], то Ф(x)
≡
0 на том же отрезке.
50
Булгаков А.А. Частотное управление асинхронными двигателями. -3-е перераб. изд. -М.: Энергоиз-
дат,1982. -216 c.

74
()
()
()
()
()
dtkkkkv
t
t
p
p
p
∫
α−α
α
γ
α−α
α++α−αα+=
1
0
2
4321
1
и далее
()
()
()
()
dtkkkkv
t
t
p
∫
α
γ
α++α−αα+=
1
0
2
43
2
21
.
Уравнение Эйлера в этом случае будет записано в виде
0=
α
∂
∂
F
. После соответствующих преоб-
разований можно получить связь между относительными значениями частоты тока статора, частоты
вращения ротора электродвигателя и абсолютным скольжением откуда можно будет сделать вывод о
том, что для обеспечения минимального уровня электромагнитных потерь должно быть реализовано
управление асинхронным электродвигателем с постоянным абсолютным скольжением. Это означает
реализацию обратной связи в виде
α=α
р
+β, где α - относительное значение частоты тока статора, α
р
–
относительное значение частоты вращения ротора
51
.
9.ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
9.1.ФУНКЦИОНАЛЫ ВИДА
()
dxy,...,y,y,y,...,y,y,xF
x
o
x
nn
∫
′′′
1
2121
52
Для получения необходимых условий экстремума функционала v более общего вида
[]
()
dxy,...,y,y,y,...,y,y,xFy,...,y,yv
x
o
x
nnn
∫
′′′
=
1
212121
при заданных граничных значениях всех функций будем варьировать лишь одну из функций
y
j
(x)
(
j=1,2,…,n), оставляя все остальные функции неизменными. При этом исходный функционал превратит-
ся в функционал, зависящий лишь от одной варьируемой функции, например от
y
j
(x) и, следовательно,
функция, реализующая экстремум, должна удовлетворять уравнению Эйлера
0=−
′
i
y
i
y
F
dx
d
F
.
Так как это рассуждение применимо к любой функции y
i
(i=1,2,…,n), то мы получим систему
дифференциальных уравнений второго порядка
()
n,...,,i,F
dx
d
F
i
y
i
y
21 0 ==−
′
.
51
Заметим сразу, что больше подобным образом (подстановкой связей-условий в подынтегральное вы-
ражение функционала) мы решать задачи не будем, а используем рассматриваемый далее аппарат ре-
шения вариационных задач на условный экстремум.
52
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.:Наука, 1969. –424 с.
75
9.2.ФУНКЦИОНАЛЫ, ЗАВИСЯЩИЕ ОТ ПРОИЗВОДНЫХ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
Исследуем на экстремум функционал
()
[]
() ()
()
()
()
dxxy,...,xy,xy,xFxyv
x
o
x
n,
∫
=
1
.
Рассмотрим однопараметрическое семейство функций
(
)() ()
(
)
[]
xyxyxy,xy
−
α+
=
α
&&&
или
()()
yxy,xy αδ+=α
.
Если рассматривать значение функционала только на кривых семейства
y=y(x,α), то функционал
превратится в функцию параметра
α, достигающую экстремума при α=0. Следовательно,
()
[]
0
0
=αδ+
α∂
∂
=α
yxyv
. Эта производная называется вариацией функционала
()()
()
()
()
()
()
.dxyF...yFyFyF
,xy,...,,xy,,xy,xF
d
d
v
x
o
x
n
n
y
yyy
x
o
x
n
∫
∫
δ++
′′
δ+
′
δ+δ=
=
αα
′
α
α
=δ
′′′
=α
1
0
1
Интегрируем по частям второе слагаемое в правой части один раз, третье слагаемое – два
раза и т.д., последнее слагаемое –
n раз.
Принимая во внимание граничные условия, в силу которых при
x=x
o
и при x=x
1
вариации
()
0
1
=δ==
′′
δ=
′
δ=δ
−n
y...yyy
, получим
()
()
ydxF
dx
d
...F
dx
d
F
dx
d
Fv
x
o
x
n
y
n
n
n
yyy
δ
−+++−==δ
∫
′′′
1
2
2
1
и далее, в силу основной леммы вариационного исчисления получим
уравнение Эйлера-Пуассона
()
()
01
2
2
=−+++−
′′′
n
y
n
n
n
yyy
F
dx
d
...F
dx
d
F
dx
d
F
.
9.3.ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ
53
Ранее, при исследовании функционалов предполагалось, что граничные точки (x
o
,y
o
) и (x
1
,y
1
) за-
даны.
Предположим теперь, что одна или обе граничные точки могут перемещаться. Например, у
функционала
()()
dttMMJ
t
t
∫
−=
0
2
3
верхний предел интегрирования не определен. Тогда класс допус-
тимых кривых расширяется, - кроме кривых сравнения, имеющих общие граничные точки с исследуемой
кривой, можно уже брать и кривые со смещенными граничными точками.
53
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.:Наука, 1969. –424 с.

76
Поэтому, если на какой-нибудь кривой y=y(x) достигается экстремум в задаче с подвижными гра-
ничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых,
имеющие общие граничные точки с кривой
y=y(x), и, следовательно, должно быть выполнено основное,
необходимое для достижения эксремума в задаче с неподвижными границами условие – функция
y=y(x)
должна быть решением уравнения Эйлера
0=−
′
yy
F
dx
d
F
.
Общее решение уравнения Эйлера содержит две произвольные постоянные, для определения ко-
торых необходимо иметь два условия. В задаче с неподвижными граничными точками такими условиями
были
y(x
o
)=y
o
и y(x
1
)=y
1
.
В задаче с подвижными границами одно или оба эти условия отсутствуют и недостающие усло-
вия для определения произвольных постоянных общего решения уравнения Эйлера должны быть полу-
чены из основного необходимого условия экстремума – равенства нулю вариации
δv.
Так как в задаче с подвижными границами экстремум достигается лишь на решениях
y=y(x,
C
1
,C
2
) уравнения Эйлера, то в дальнейшем можно рассматривать значение функционала лишь на функ-
циях этого семейства. При этом функционал
v[y(x,C
1
,C
2
)] превращается в функцию параметров C
1
и C
2
и
пределов интегрирования
x
o
и x
1
, а вариация функционала совпадает с дифференциалом этой функции.
Для упрощения будем считать, что одна из граничных точек закреплена, а другая может перемещаться
(см. рисунок ниже).
Вычислим вариацию функционала
v[y(x,C
1
)] на экстремалях пучка y=y(x, C
1
) при перемещении
граничной точки из положения (
x
1
,y
1
) в положение (x
1
+δx
1
,y
1
+δy
1
). Так как функционал на кривых пучка
превратился в функцию
x
1
и y
1
, то его вариация совпадает с дифференциалом этой функции. Выделим из
приращения
∆v главную, линейную по отношению к δx
1
, δy
1
часть:
(9.1)
()()
()()()
[]
.dxy,y,xFyy,yy,xFdxyy,yy,xF
dxy,y,xFdxyy,yy,xFv
x
o
x
xx
x
x
o
x
xx
o
x
∫∫
∫∫
′
−
′
δ+
′
δ++
′
δ+
′
δ+=
=
′
−
′
δ+
′
δ+=∆
δ+
δ+
111
1
111
Первое слагаемое преобразуем с помощью теоремы о среднем значении
()
1
11
11
1
xFdxyy,yy,xF
xxx
xx
x
δ=
′
δ+
′
δ+
δΘ+=
δ+
∫
, где 0<θ<1. В силу непрерывности функции F
будем иметь
()
1
111
ε
+
′
=
=δΘ+= xxxxx
y,y,xFF
,
где
ε
1
→0 при δx
1
→0 и δy
1
→0.
В итоге
()
111
1
11
1
xxFdxyy,yy,xF
xx
xx
x
δε+δ=
′
δ+
′
δ+
=
δ+
∫
.
Второе слагаемое правой части (9.1) преобразуем путем разложения подынтегральной функции
по формуле Тейлора
77
()()
[]
() ()
[]
,Rdxyy,y,xFyy,y,xF
dxy,y,xFyy,yy,xF
x
x
yy
x
x
o
o
∫
∫
+
′
δ
′
+δ
′
=
=
′
−
′
δ+
′
δ+
′
1
1
1
где R
1
является бесконечно малой более высокого порядка, чем δy или δy
1
. В свою очередь ли-
нейная часть
[]
∫
′
δ+δ
′
1
x
x
yy
o
dxyFyF
может быть преобразована путем интегрирования по частям второго
слагаемого подынтегральной функции к виду
∫
δ
−+δ
′′
1
1
x
x
yy
x
x
y
o
o
ydxF
dx
d
FyF
.
Значения функционала берутся лишь на экстремалях, следовательно,
0≡−
′
yy
F
dx
d
F
.
Так как граничная точка (
x
o
,y
1
) закреплена, то
0
0
=
δ
=xx
y
. Следовательно,
[][]
1
1
xx
y
x
x
yy
yFdxyFyF
o
=
′′
δ=
′
δ+δ
∫
.
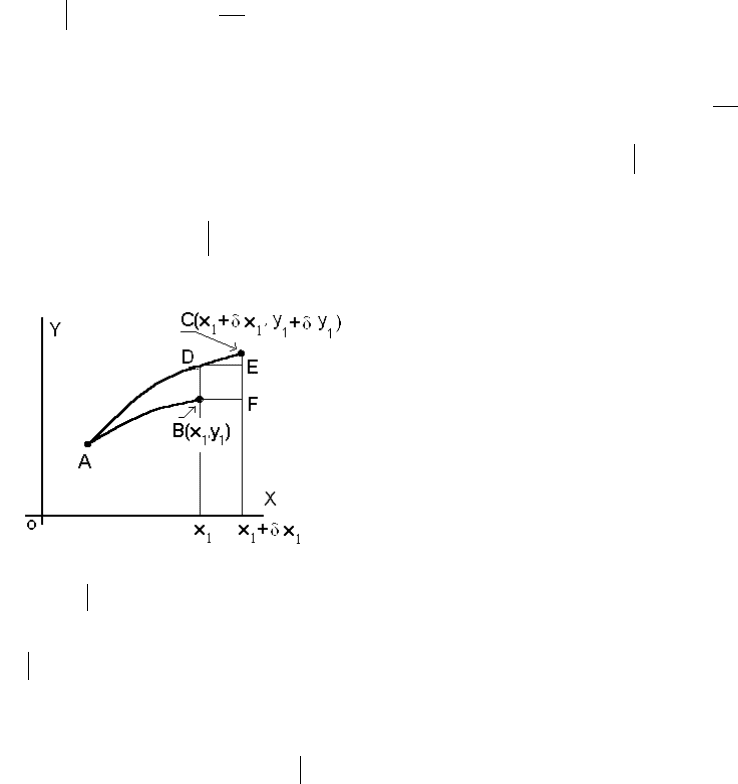
Из рисунка видно, что
(
)
;ECCFBD;xxyEC;yFC;yBD
xx
−
=
δ
′
≈
δ=δ=
=
111
1
или
()
111
1
xxyyy
xx
δ
′
−δ≈δ
=
.
Окончательно можно записать:
()
1
1
11
1
xFdxyy,yy,xF
xx
xx
x
δ≈
′
δ+
′
δ+
=
δ+
∫
;

78
()()
[]
()()
111
1
1
xxyyFdxy,y,xFyy,yy,xF
xx
y
x
x
o
δ
′
−δ⋅≈
′
−
′
δ+
′
δ+
=
′
∫
.
Следовательно,
(
)()
()
.yFxFyF
xxyyFxFv
xx
y
xx
y
xx
y
xx
11
1111
11
1
1
δ+δ
′
−=
=δ
′
−δ⋅+δ=δ
=
′
=
′
=
′
=
Если вариации
δx
1
и δy
1
независимы, то основное необходимое условие экстремума δv=0 приоб-
ретает вид
()
.F,FyF
xx
y
xx
y
0 0
11
==
′
−
=
′
=
′
Если между
δx
1
и δy
1
имеется связь, т.е. y
1
=ϕ(x
1
), тогда
(
)
111
xxy δ
ϕ
′
≈
δ
и, следовательно,
()
[
]
0
1
=
′
−
ϕ
′
+
=
′
xx
y
FyF
.
Последние выражения носят название
условий трансверсальности.
9.4.ПРИМЕНЕНИЕ РЕЗУЛЬТАТОВ
В теории классического вариационного исчисления определены условия достижения экстремума
функционалами вида
()
∫
′′
=
x
x
nn
o
dxy,...,y,y,...,y,xFJ
11
,
в задаче с подвижными границами.
Основными из них являются уравнения Эйлера-Лагранжа и условия трансверсальности. Они за-
писываются так:
0,F
dx
d
F
ii
yy
=−
′
(i=1,2,…,n) - уравнения Эйлера-Лагранжа;
=
=
′
−
∑
∑
=
′
=
′
.F
,FyF
n
i
y
n
i
yi
i
i
0
0
1
1
- условия трансверсальности.
Здесь
.n,..,,i,
y
F
F,
y
F
F
i
y
i
y
ii
21 =
′
∂
∂
=
∂
∂
=
′
Во многих работах по оптимальному управлению непрерывными системами
54
определены мощ-
ные алгоритмы построения аналитических конструкций оптимальных регуляторов для систем, поведение
54
Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. -М.: Наука,1973. -446 c.
Кротов В.Ф., Букреев В.З., Гурман В.И. Новые методы вариационного исчисления в динамике полета. -
М.: Машиностроение,1969. -288 c.
Крутько П.Д., Попов Е.П. Обратные задачи динамики управляемых систем и оптимальные процессы
//ДАН СССР,т.263. -1982. -N5. -С.1078-1082.
Крутько П.Д. Обратные задачи динамики управляемых систем. -М.: Наука,1987. -304 c.
79
которых описывается совокупностями обыкновенных дифференциальных уравнений и уравнениями в
частных производных. Цель управления для большинства прикладных задач записывается обычно в виде
квадратичного функционала.
Эффективность применения этих методов для решения задач управления электроприводом гор-
ных машин подтверждена в ряде работ по управлению их состоянием
55
. Оговоримся, что под эффектив-
ностью здесь понимается возможность получения решения в виде алгебраической или дифференциаль-
ной зависимости управляющих воздействий от параметров, характеризующих состояние системы горной
машины, т.е. возможность получения оптимального результата без использования скользящих режимов.
Получаемые аналитические конструкции оптимальных регуляторов имеют один недостаток -
строго детерминированную связь между управляющим воздействием и параметрами состояния горной
машины. Такие связи не всегда могут быть физически реализованы в приводах горных машин из-за
сложностей оснащения машины, работающей в специфических условиях, датчиками состояния.
В этой связи возникает проблема поиска возможностей построения таких управляющих конст-
рукций, которые могут быть физически реализованы именно в приводах горных машин.
Для этого варианта рассмотрим случай, когда целевой функционал не содержит производных.
При этом условия обеспечения экстремума (условия оптимальности) перепишутся в виде
,F,F
i
y
0 0 ==
а сам функционал запишем в виде
()
∫
=
t
o
t
,dt,fJ
0
ux
где
(
)
n
x,...,x,x
21
=x
- вектор-функция фазовых координат объекта, характеризующих его со-
стояние,
(
)
m
u,...,u,u
21
=u
- вектор-функция управления.
При этом движение объекта описывается совокупностью дифференциальных связей (уравнений
движения)
()
ux,fx =
&
, где
(
)
n
f,...,f,ff
21
=
, а точка вверху переменной означает операцию дифферен-
цирования по времени.
В новых обозначениях условия оптимальности перепишутся
() ()
0 0 =
∂
∂
=
∂
∂
i
o
i
o
u
,f
,
x
,f uxux
,
(
)
.,f
o
0=ux
Дифференцирование последнего выражения (
(
)
0=ux,f
o
) по времени дает
()
()
()
∑∑
=
=
=⋅
∂
∂
+⋅
∂
∂
=
n
i
m
i
i
i
oi
i
o
o
dt
du
u
,f
dt
dx
x
,f
,f
dt
d
11
0
uxux
ux
,
Кунцевич В.М., Лычак М.М. Синтез систем автоматического управления с помощью функций Ляпунова.
-М.: Наука,1977. -400 c.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптималь-
ных процессов .-4-е изд. -М.: Наука,1983. -392 c.
55
Гаврилов П.Д., Ещин Е.К. Управление динамикой скребкового конвейера с помощью частотно-
управляемого электропривода //Физ.-технич. проблемы разраб .полезн. иск.. -1980. -N6. -С.72-77.
Гаврилов П.Д., Ещин Е.К. Снижение уровня динамической нагруженности скребкового конвейера при
помощи асинхронного электропривода. //Изв.вузов.Горный журнал. -1978. -N11. -С.99-105.
80
или
.u
u
f
f
x
f
i
m
i
i
i
n
i
i
0
1
0
1
0
=⋅
∂
∂
+⋅
∂
∂
∑∑
==
&
Это означает, что могут существовать условия достижения экстремума в формах
()
=⋅
∂
∂
+⋅
∂
∂
=⋅
∂
∂
∑∑
∑
==
=
,u
u
f
f
x
f
.
,f
x
f
.
i
p
i
i
i
k
i
i
i
n
i
i
02
01
1
0
1
0
1
0
&
ux,
Последнее означает, что для поиска аналитических конструкций управляющих устройств (УУ)
возможно использование произвольных совокупностей произведений частных производных от подынте-
грального выражения функционала по фазовым координатам на правые части уравнений движения.
Из этого следует, что возможно построение множества аналитических конструкций управляю-
щих устройств. Построение может осуществляться как в форме алгебраических связей управляющих
воздействий с фазовыми координатами, так и в форме дифференциальных связей
.
9.5.УПРАВЛЕНИЕ АСИНХРОННЫМ ЭЛЕКТРОДВИГАТЕЛЕМ
Рассмотрим в качестве примера задачу управления асинхронным электродвигателем. Целью
управления будем считать обеспечение необходимого значения электромагнитного момента двигателя.
() () () ()()
dttttt
L
k
pMJ
t
t
rvsusvru
s
r
∫
ΨΨ−ΨΨ
′
−=
0
2
3
2
3
Уравнения движения запишем в системе вращающихся координат
u,v:
()
()
Ψω−αω−Ψ
′
+Ψ
′
−=
Ψ
Ψω−αω+Ψ
′
+Ψ
′
−=
Ψ
Ψαω−Ψ
′
+Ψ
′
−=
Ψ
Ψαω+Ψ
′
+Ψ
′
−=
Ψ
.pk
L
R
L
R
dt
d
,pk
L
R
L
R
dt
d
,k
L
R
L
R
U
dt
d
,k
L
R
L
R
U
dt
d
runsvs
r
r
rv
r
r
rv
rvnsus
r
r
ru
r
r
ru
sunrvr
s
s
sv
s
s
sv
sv
svnrur
s
s
su
s
s
su
su
Образуем выражения
() ()
() ()
Ψ−
′
=
Ψ∂
∂
Ψ−
′
−=
Ψ∂
∂
Ψ−
′
−=
Ψ∂
∂
Ψ−
′
=
Ψ∂
∂
.MM
L
pk
f
,MM
L
pk
f
,MM
L
pk
f
,MM
L
pk
f
su
r
s
rv
ru
r
s
sv
sv
r
s
ru
rv
r
s
su
3
0
3
0
3
0
3
0
3
3
3
3
Составим произвольные связи
,f
f
f
f
s
v
s
u
0
4
0
3
0
=
Ψ∂
∂
+
Ψ∂
∂
,f
f
f
f
rvru
0
4
0
3
0
=
Ψ∂
∂
+
Ψ∂
∂
