Ещин Е.К. Моделирование систем управления электромеханическими объектами
Подождите немного. Документ загружается.

61
begin
Rele;
Ua:=1140.0*sqrt(2.0)*sin(314.0*x);
Ub:=1140.0*sqrt(2.0)*sin(314.0*x-1.57);
for i:=1 to N_dvig do
M[i]:=c[i]*(y[4*i-1]*y[4*i-2]-y[4*i-3]*y[4*i]);
for i:=1 to N_dvig do begin
Isa[i]:=(y[4*i-3]-Kr[i]*y[4*i-1])/Lps[i];
Isb[i]:=(y[4*i-2]-Kr[i]*y[4*i ])/Lps[i];
Ira[i]:=(y[4*i-1]-Ks[i]*y[4*i-3])/Lpr[i];
Irb[i]:=(y[4*i ]-Ks[i]*y[4*i-2])/Lpr[i];
end;
for i:=1 to N_dvig do begin
f3[i]:=-Rr[i]*Ira[i]-p*y[4*N_dvig+i]*y[4*i];
f4[i]:=-Rr[i]*Irb[i]+p*y[4*N_dvig+i]*y[4*i-1];
end;
for i:=1 to N_dvig do begin
S_1:=0;
for j:=1 to N_dvig do
S_1:=S_1+Lk[0]*Kr[j]*f3[j]/Lps[j]-Rk[0]*Isa[j];
S_2:=0;
Nu:=int((i+Nm-1)/Nm);
for j:=trunc(Nu*Nm-Nm+1) to trunc(Nu*Nm) do
S_2:=S_2+Lk[trunc(Nu)]*Kr[j]*f3[j]/Lps[j]- Rk[trunc(Nu)]*Isa[j];
item_a[i]:=Ua+S_1+S_2-Rs[i]*Isa[i];
end;
for i:=1 to N_dvig do begin
S_1:=0;
for j:=1 to N_dvig do
S_1:=S_1+Lk[0]*Kr[j]*f4[j]/Lps[j]-Rk[0]*Isb[j];
S_2:=0;
Nu:=int((i+Nm-1)/Nm);
for j:=trunc(Nu*Nm-Nm+1) to trunc(Nu*Nm) do
S_2:=S_2+Lk[trunc(Nu)]*Kr[j]*f4[j]/Lps[j]-Rk[trunc(Nu)]*Isb[j];
item_b[i]:=Ub+S_1+S_2-Rs[i]*Isb[i];
end;
Matrica;
Treugol;
delta:=1;
for i:=1 to N_dvig do delta:=delta*a[i,i];
for i:=1 to N_dvig do begin
Matrica;
for j:=1 to N_dvig do a[j,i]:=item_a[j];
Treugol;
delta_1:=1;
for k:=1 to N_dvig do delta_1:=delta_1*a[k,k];
f[4*i-3] :=delta_1/delta;
62
Matrica;
for j:=1 to N_dvig do a[j,i]:=item_b[j];
Treugol;
delta_1:=1;
for k:=1 to N_dvig do delta_1:=delta_1*a[k,k];
f[4*i-2] :=delta_1/delta;
f[4*i-1] :=f3[i];
f[4*i ] :=f4[i];
f[4*N_dvig+i]:=4*(M[i])/GD2[i];
end;
{== Место для размещения уравнений движения механики ======}
end;
{-----------------------------------------------------------}
Procedure Vivod;
begin
for i:=1 to N_dvig do begin
for j:= 1 to N_dvig do begin
write(a[i,j]:10:5,' ');
end;
writeln;
end;
writeln;
end;
6.3.ПРИМЕР РАСЧЕТА
Рассмотрим пример, соответствующий рис.6.1. В этом варианте количество электродвигателей в
модулях
Nm=2, а количество модулей равно трем, т.е. рассмотрим одновременно происходящие элек-
тромеханические динамические процессы, например, в 4-х двигательном приводе забойного скребкового
конвейера и 2-х двигательном приводе комбайна при последовательном пуске электродвигателей систе-
мы.
Примем длины кабелей: до головного привода конвейера от РПЛ- №1
L
1
=100 м, до хвостового
привода (от РПЛ-№1 через РПЛ-№2)
L
2
=250 м, до привода комбайна от РПЛ-№1 L
3
=200 м. Привод кон-
вейера оснащен двигателями АВР280L4, привод комбайна - двигателями ЭКВ4У. Длина общей части
кабельной сети (от ПУПП №1 до РПЛ-№1)
L
0
=100 м. Некоторые результаты моделирования процессов
последовательного пуска всех электродвигателей системы представлены на рис.6.6, 6.7.
1200
1250
1300
1350
1400
1450
1500
1550
1600
1650
0 0.2 0 .4 0 .6 0 .8 1 1.2 1 .4
t, c
Амплитуда напряжения U,В
3
1
2
63
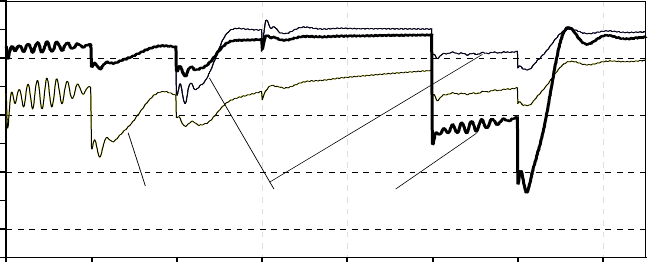
Рис.6.6. Изменение напряжений на электродвигателях конвейера и комбайна при последовательном пус-
ке (напряжения на двигателях: 1 –хвостового привода, 2 – головного привода, 3 – комбайна)
Полученные зависимости для этого примера дают возможность оценить предельные значения и
длительность пиковых значений тока (рис.6.7) каждого электродвигателя и, естественно, суммарных пи-
ков токов в сети. По данным рис.6.6 имеется возможность оценить величины уровней напряжений на
электродвигателях в режимах пуска.
Таким образом, на основе использования математической модели (6.5) возможно получение не-
обходимой информации о состоянии электромеханических систем горных машин при преобразовании
электрической энергии в сети электроснабжения добычного участка для широкого спектра режимов ра-
боты горных машин, включая аварийные.
0
400
800
1200
1600
2000
0 0. 2 0.4 0.6 0. 8 1 1.2 1.4
t,
c
Амплит
уд
а тока I
,А
1
2
3
4 5
6
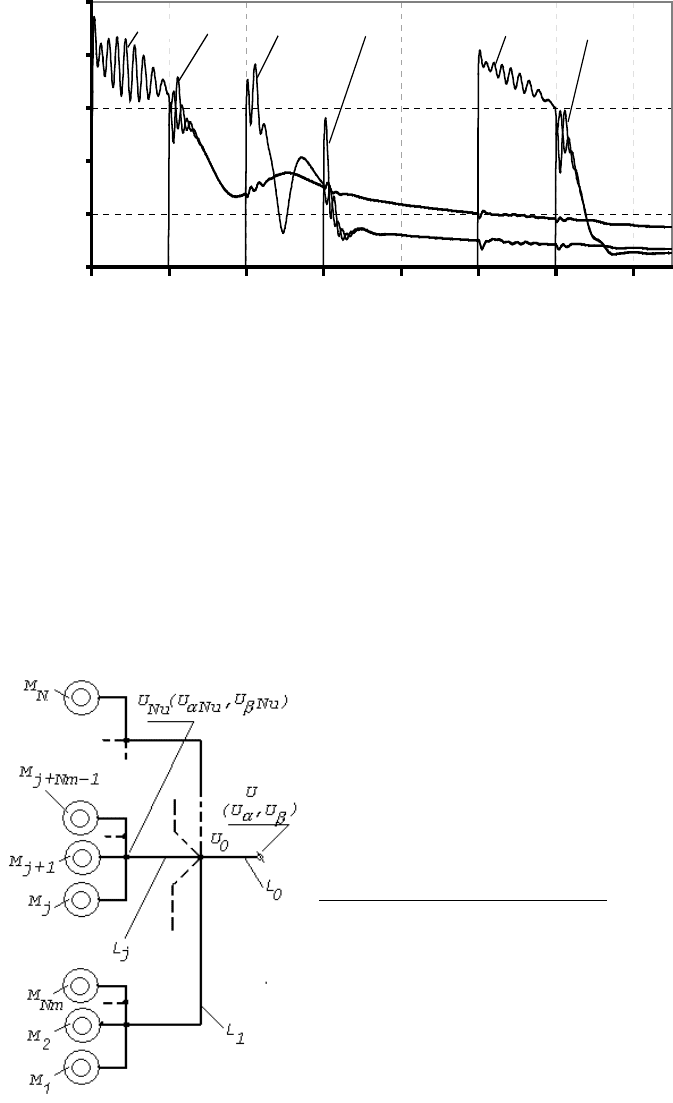
Рис. 6.7. Изменения токов электродвигателей конвейера и комбайна при последовательном пуске (токи:
1,2 –хвостового привода конвейера, 3,4 –головного привода конвейера, 5,6 –двигателей комбайна)
7.МОДЕЛЬ АСИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ В СЕТИ ЭЛЕКТРОСНАБЖЕНИЯ ПРОИЗВОЛЬНОЙ
СТРУКТУРЫ
В [1]
37
рассмотрено моделирование процессов электромеханического преобразования энергии в
сети электроснабжения со структурой, характерной для добычных участков угольных шахт (рис.1).
Обоснованием необходимости рассмотрения процессов, происходящих одновременно во всех компонен-
тах сети, является соизмеримость мощностей используемых электродвигателей и значительные длины
питающих кабелей. Там же получена математическая модель асинхронного электродвигателя, работаю-
щего в этой сети, которая, строго говоря, является одним из возможных вариантов структур сети элек-
троснабжения.
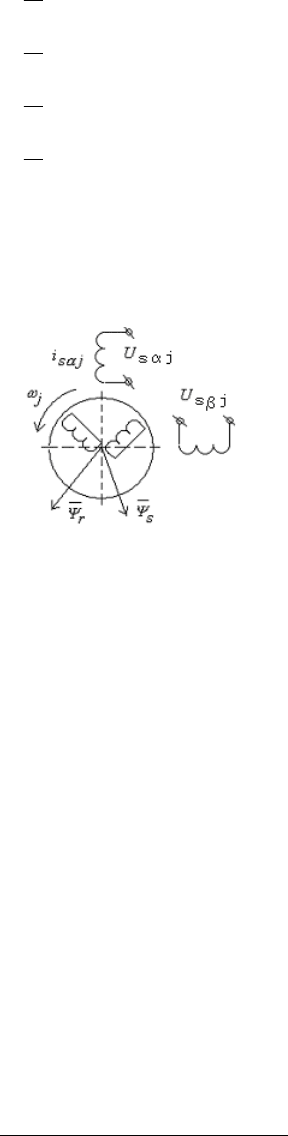
Рис.7. 1. Схема электроснабжения приводов горных машин
37
Ещин Е.К. Расчеты электромеханических переходных процессов в системе электроснабжения
горных машин // Электротехника.-1999. №3. С.41-44
64
Состояние каждого j-го двигателя, работающего в одиночном варианте, может быть описано со-
вокупностью дифференциальных связей
38
]
(7.1)
где параметры, начинающиеся с
R и индексами s, r - актив-
ные сопротивления обмоток статоров и роторов АД,
p
j
- число пар
полюсов,
ω
j
- геометрическая угловая скорость вращения ротора
электродвигателя,
Ψ
s
Ψ
r
,
с индексами
α
,
β
- составляющие потокос-
цеплений статора и ротора по осям неподвижной системы коорди-
нат,
j - в индексном обозначении определяет номер двигателя.
Ясно, что состояние каждого
j-го электродвигателя опреде-
ляется скоростью вращения ротора
ω
j
и
jsjs
U,U
βα
- составляю-
щими напряжений статоров двигателей.
В этой связи рассмотрим алгоритм формирования упомянутых напряжений в сети электроснаб-
жения произвольной структуры с целью синтеза математической модели асинхронного электродвигателя
для этой сети.
Очевидно, что любую конкретную конфигурацию сети с N асин-
хронными электродвигателями можно получить на основе структуры,
изображенной на рис.3 и, в частности, для 4 уровней – на рис.4. определяя
при помощи логических переключателей необходимые рабочие ветви се-
ти электроснабжения.
Обозначения на рисунках: индекс 0 – соответствует общему уча-
стку питающего кабеля. Для остальных кабелей первый индекс означает
принадлежность уровню, второй – ветви соответствующего уровня. Диа-
пазон изменения значений уровней
k
∈
(1,M), диапазон изменения индек-
сов ветвей
v∈(1,2
k
). При помощи такой системы индексации будем иден-
тифицировать конкретные кабельные участки (ветви) системы электро-
снабжения. Например,
kvkv
R,L
- индуктивность и активное сопротивле-
ние кабельного участка
k-го уровня, v-й ветви, являющиеся функциями
его длины.
38
Ковач К., Рац И. Переходные процессы в машинах переменного тока. -М. -Л.: Госэнергоиз-
дат,1963. -744 c.
Р
ис.7. 2. Расчетная схе-
м
а j-го асинхронного
электродвигателя с ко-
р
откозамкнутым рото-
р
ом для (1)
,fp+iR
dt
d
,fpiR
dt
d
,iRU
dt
d
,iRU
dt
d
jjrjjjrrjjr
jjrjjjrrjjr
jssjjsjs
jssjjsjs
=Ψ−=Ψ
=Ψ−−=Ψ
−=Ψ
−=Ψ
4
3
αββ
βαα
βββ
ααα
ω
ω
65
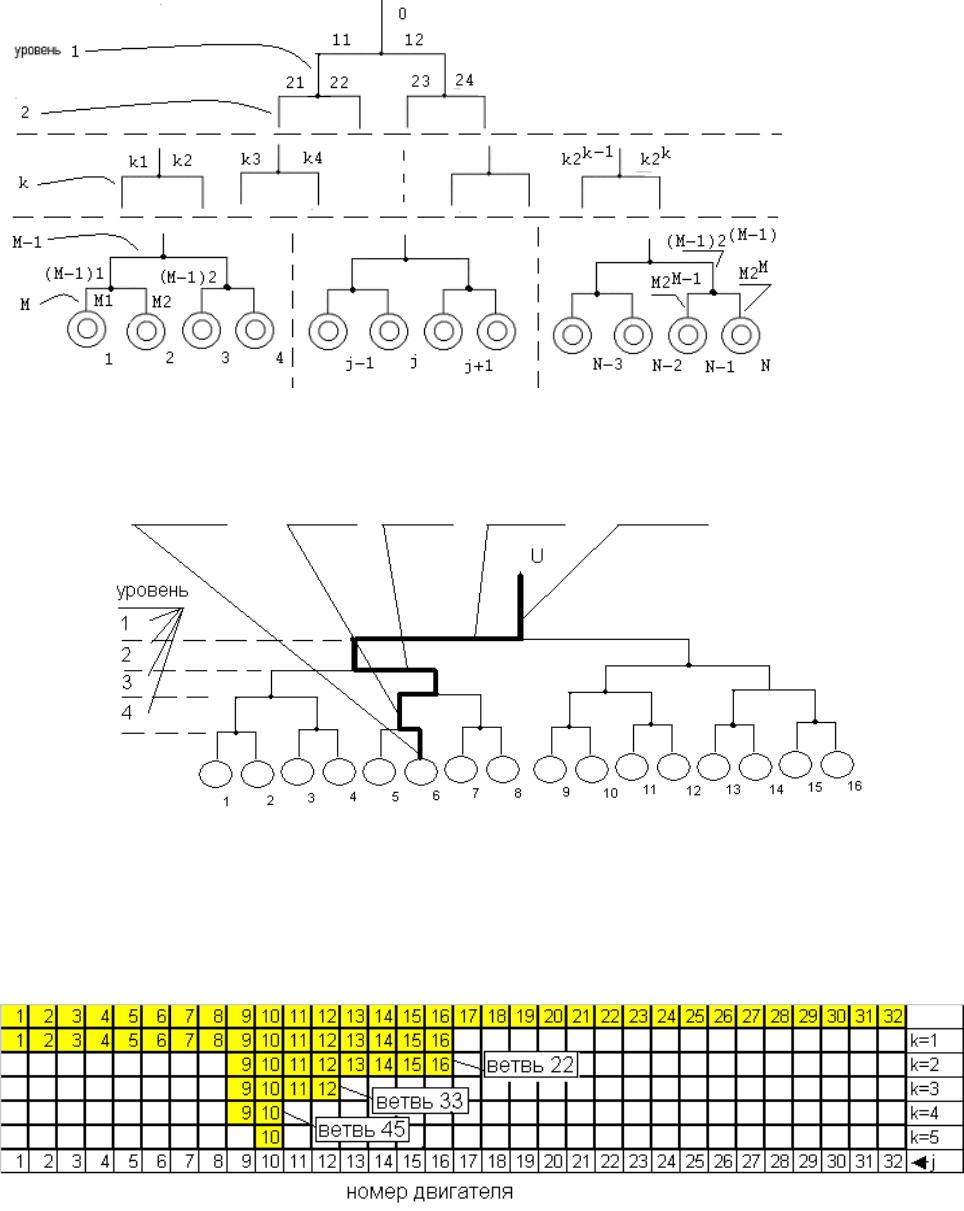
Рис. 7.3. Общая структура сети электроснабжения с электродвигательной нагрузкой
∑∑∑∑
====
16
1
8
1
8
5
6
5
6
i
si
i
si
i
si
i
sis
I I I I I
Рис. 7.4. Четырех уровневая структура сети электроснабжения
Основная проблема при определении напряжений на обмотках статора
j-го электродвигателя для
рассматриваемой структуры сети – идентификация пути от двигателя до источника питания и идентифи-
кация двигателей, токи которых участвуют в формировании суммарных уровней падений напряжений на
каждом кабельном отрезке - ветви (см., например, выделенный путь от 6-го двигателя на рис.4 и рис.5)
Рис. 7.5. Пример. Номера двигателей, участвующих в формировании падений напряжений на участках
5-и уровневой кабельной сети для 10-го электродвигателя

66
Вводя переменные и выражения для определения их значений
+=+
=
+=
−
−−
−
−
− km
kmkm
km
km
km
j
intv ,
j
intl ,
j
intl
2
122
2
2
2
1
10
, (7.2)
где
l
0
, l
1
– начальное и конечное значения индекса, определяющего номер двигателя, токи которо-
го участвуют в формирование падения напряжения на
k,v –участке кабельной сети, будем иметь искомое
напряжение на обмотке статора
j-го электродвигателя (для составляющей по координатной оси α)
39
в ви-
де:
∑∑∑∑
====
+−
+−=
N
i
isis
m
k
l
ll
lsv,k
l
ll
lsv,kjs
IRI
dt
d
LIRI
dt
d
LUU
1
00
1
1
0
1
0
αααααα
+
+
+
+
+
+
+
+
+
+
+
+
+
+
∑
∑
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
=
=
16
1
0
16
1
0
8
1
11
8
1
11
8
5
22
8
5
22
6
5
33
6
5
33
646
646
i
is
i
is
i
is
i
is
i
is
i
is
i
is
i
is
s
s
IR
I
dt
d
L
IR
I
dt
d
L
IR
I
dt
d
L
IR
I
dt
d
L
IR
I
dt
d
L
α
α
α
α
α
α
α
α
α
α
Рис. 7.6. Пример. Падение напряжения на участках кабельной сети до 6-го двигателя
и далее
∑∑∑∑∑∑
======
−−
−
−=
N
i
is
N
i
is
m
k
l
ll
lsv,k
m
k
l
ll
lsv,kjs
IRI
dt
d
LIRI
dt
d
LUU
1
0
1
0
11
1
0
1
0
αααααα
. (7.3)
(Нужно иметь в виду, что в средах
Delphi, Pascal численная реализация выражения
−km
i
int
2
осуществляется как
()
(
)()()
2lnkmexpiint ∗−
или
(
)
(
)
(
)
(
)
2lnkmexpitrunc
∗
−
и поэтому, например,
при
i=6, m=4, k=3 значения этих выражений 2, а не 3 и т.п.)
Известны отношения
,
L
k
L
i ,
L
k
L
i
jr
'
sj
rj
'
sj
js
jsjr
'
sj
rj
'
sj
js
js
β
β
βα
α
α
Ψ−
Ψ
=Ψ−
Ψ
=
которые после дифференцирования можно представить следующим образом
39
Для составляющей напряжения по оси
β
-записи аналогичны.
67
.f
L
k
dt
d
L
dt
di
,f
L
k
dt
d
L
dt
di
j
'
sj
rjjs
'
sj
js
j
'
sj
rjjs
'
sj
js
43
11
−
Ψ
⋅=−
Ψ
⋅=
ββαα
(7.4)
В (4) и далее
'
,
sjrj
Lk
– коэффициенты электромагнитной связи и переходные индуктивности
двигателей (определяются по
40
).
Используя (7.4) в (7.3), получим последовательно
,IRIRf
L
k
dt
d
L
L
f
L
k
dt
d
L
LUU
N
i
is
N
i
m
k
l
ll
lsv,ki
'
si
riis
'
si
m
k
l
ll
l
'
sl
rlls
'
sl
v,kjs
∑∑∑∑
∑∑
====
==
−
−
−
Ψ
⋅−
−
−
Ψ
⋅−=
1
0
11
3
0
1
3
1
0
1
0
1
1
αα
α
α
αα
,IRIRf
L
k
Lf
L
k
L
dt
d
L
L
dt
d
L
LUU
N
i
is
m
k
l
ll
lsv,k
N
i
i
'
si
ri
m
k
l
ll
l
'
sl
rl
v,k
N
i
is
'
si
m
k
l
ll
ls
'
sl
v,kjs
∑∑∑∑∑∑
∑∑∑
======
===
−
−
+
+
+
Ψ
⋅−
Ψ
⋅−=
1
0
11
3
0
1
3
1
0
1
1
0
1
0
1
0
11
αα
αα
αα
(7.5)
Далее, объединяя (7.1) и (7.5), получим для
j-го двигателя искомую математическую модель
(7.6)
,fp+iR
dt
d
,fpiR
dt
d
,iRIR
IRf
L
k
Lf
L
k
L
U
dt
d
L
L
dt
d
L
L
dt
d
,iRIR
IRf
L
k
Lf
L
k
L
U
dt
d
L
L
dt
d
L
L
dt
d
jjrjjjrrj
jr
jjrjjjrrj
jr
jssj
N
i
is
m
k
l
ll
lsv,k
N
i
i
'
si
ri
m
k
l
ll
l
'
sl
rl
v,k
N
i
is
'
si
m
k
l
ll
ls
'
sl
v,k
js
jssj
N
i
is
m
k
l
ll
lsv,k
N
i
i
'
si
ri
m
k
l
ll
l
'
sl
rl
v,k
N
i
is
'
si
m
k
l
ll
ls
'
sl
v,k
js
=Ψ−=
Ψ
=Ψ−−=
Ψ
−−
−
−
+
+
+=
Ψ
⋅+
Ψ
⋅+
Ψ
−−
−
−
+
+
+=
Ψ
⋅+
Ψ
⋅+
Ψ
∑
∑∑∑∑∑
∑∑∑
∑
∑∑∑∑∑
∑∑∑
=
=====
===
=
=====
===
4
3
1
0
11
4
0
1
4
1
0
1
1
0
11
3
0
1
3
1
0
1
1
0
1
0
1
0
1
0
1
0
1
0
11
11
αβ
β
βα
α
ββ
β
β
βββ
αα
α
α
αα
α
ω
ω
40
Ковач К., Рац И. Переходные процессы в машинах переменного тока. -М. -Л.: Госэнергоиздат,1963. -744
c.

68
*где j∈(1,N),
+=+
=
+=
−
−−
−
−
− km
kmkm
km
km
km
j
intv ,
j
intl ,
j
intl
2
122
2
2
2
1
10
,
,
L
k
L
i ,
L
k
L
i
js
'
rj
sj
'
rj
jr
jrjs
'
rj
sj
'
rj
jr
srj
β
β
βα
α
Ψ−
Ψ
=Ψ−
Ψ
=
а скорость вращения ω
j
определится с исполь-
зованием уравнений движения электропривода
()
−ΨΨ−ΨΨ=
−
cjjrjsjsjr
'
sj
rj
j
M
L
k
pJ
βαβα
ω
2
3
1
.
Для использования в расчетной практике математической модели (6) электромеханического пре-
образования энергии совокупностью асинхронных электродвигателей с короткозамкнутым ротором, на-
ходящихся в системе электроснабжения произвольной структуры, в Кузбасском государственном техни-
ческом университете на ее (модели) основе разработано программное обеспечение, которое позволяет
задавать конфигурацию и условия работы системы электроснабжения, число электродвигателей, длины и
параметры ветвей кабелей, параметры электродвигателей, последовательности включения или отключе-
ния электродвигателей для имитации реальных процессов пусков и отключений приводов горных ма-
шин, характера нагрузки на электродвигателях при моделировании режимов работы реальных горных
машин. Учет изменения активных сопротивлений и индуктивных сопротивлений рассеяния вследствие
вытеснения тока и насыщения путей рассеяния можно вести на основе зависимостей этих параметров от
скольжения, получаемых, например по
41
. На рис. 7.6, 7.7 приведены результаты исследования процессов
последовательного пуска без нагрузки трех асинхронных электродвигателей ЭВР280Д4 мощностью 160
кВт, подключенных к источнику питания через отрезки кабельной сети длиной по 500 м.
Рис. 7.6. Пример. Изменение амплитуд напряжений на обмотках статоров электродвигателей
ЭВР280L4 при пуске их в последовательности 3 – 2 – 1.
41
Постников И.М. Обобщенная теория и переходные процессы электрических машин. -М.: Высшая шко-
ла, 1975. -319 с.
Ещин Е.К., Иванов В.Л., Алешин Д.А. Автоматизация экспресс - испытаний асинхронных электродвига-
телей // Электротехника. -1995. -№5. С.59-61.
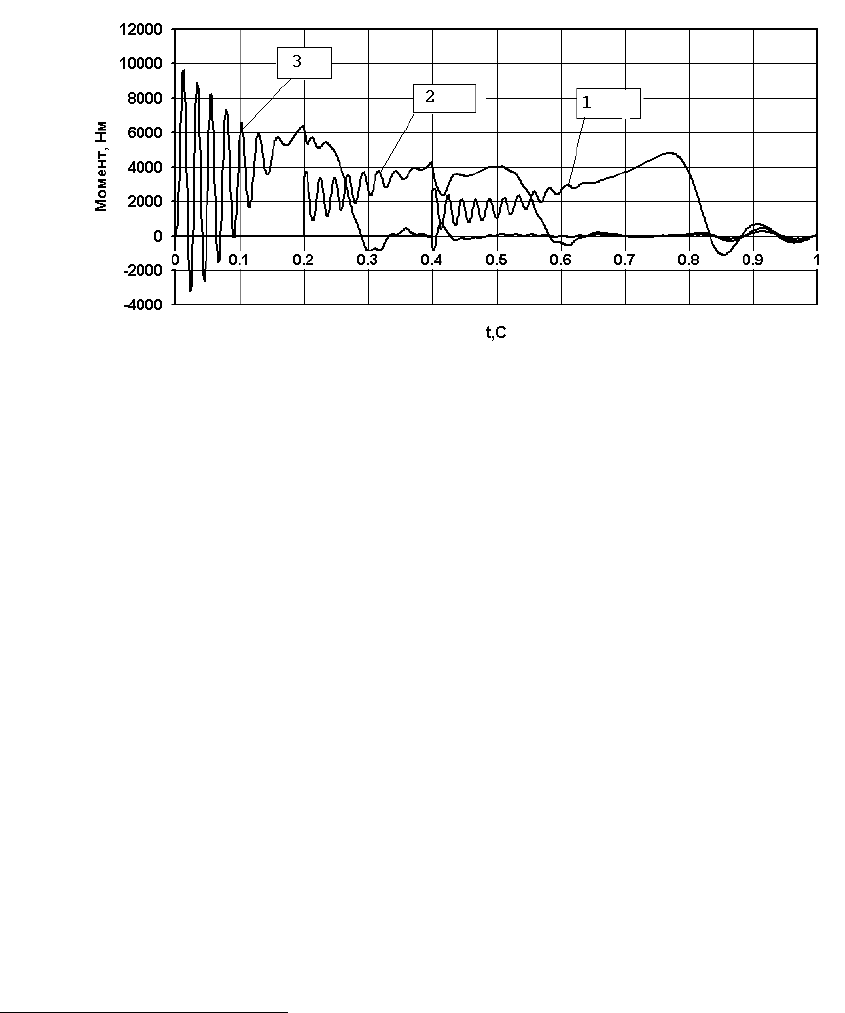
69
Рис. 7.7. Пример. Изменение электромагнитных моментов электродвигателей при последовательном
пуске без нагрузки
Таким образом, на основе использования математической модели (7.6) возможно получение не-
обходимой информации о состоянии электромеханических систем при преобразовании электрической
энергии в сети электроснабжения произвольной структуры.
8.МАТЕМАТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ
8.1.ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
42
«…Уже само название нашего предмета является чисто историческим; оно связано с одним част-
ным методом, восходящим к Эйлеру и основанным на так называемых вариациях»
43
.
Вариационное исчисление устанавливает условия, при которых
функционалы достигают своего
экстремума
44
.
8.2.ФУНКЦИОНАЛ
В свою очередь функционал определяется следующим образом. Если M – множество функций и
каждой функции
ϕ
(x), принадлежащей M относится определенное число, то говорят, что на множестве M
задан
функционал.
Есть и такая формулировка
45
. Переменная величина v называется функционалом, зависящим от
функции
x(t), если каждой функции x(t) из некоторого класса функций соответствует значение v, т.е.
42
Вариационное исчисление и оптимальное управление: Учеб. для студентов высш. техн. учеб. заведений
/ В. И. Ванько, О. В. Ермошина, Г. Н. Кувыркин; Под ред. В. С. Зарубина и А. П. Крищенко. - М. : Изд-во
МГТУ им. Н. Э. Баумана, 1999. - 487 с.
Математическая теория конструирования систем управления: Учеб. для студентов вузов, обучающих-
ся по спец. " Прикл. математика" / В. Н. Афанасьев, В. Б. Колмановский, В. Р. Носов. - 2. изд., доп. - М. :
Высшая шк., 1998. - 573 с.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.:Наука, 1969. –424 с.
43
Янг Л. Лекции по вариационному исчислению и теории оптимального управления. М.: Мир,1974. –488 с.
44
Цлаф Л.Я. Вариационное исчисление и интегральные уравнения. М.:Наука,1966. – 176 с.
45
Гноенский Л.С., Каменский Г.А., Эльсгольц Л.Э. Математические основы теории управляемых систем.
М.:Наука,1969. –512 с.

70
имеет место соответствие: функции x(t) соответствует число v. Функционал может зависеть от несколь-
ких функций и от функций нескольких независимых переменных.
Одной из первых задач вариационного исчисления была задача Ивана Бернулли (
John Bernoulli) о
брахистохроне
46
(1696 г.), которая формулируется следующим образом (Цлаф Л.Я.).
В вертикальной плоскости даны две точки О и В. По какой линии скатится тяжелая материальная
точка, оставаясь в этой плоскости, из верхней точки в нижнюю в наименьший промежуток времени? На-
чальная скорость равна нулю. Сопротивление движению также полагается равным нулю.
Задача сводится к нахождению минимума функционала
[]
.dx
)x(gy
dx
)x(dy
)x(yJ
b
o
∫
+
=
2
1
2
47
На рисунке представлена графическая иллюстрация этой
задачи.
Рассмотрим другой пример. Допустим, что по условиям выполнения некоторого технологическо-
го процесса требуется, чтобы электродвигатель в используемом для этого процесса электроприводе раз-
вивал заданное значение электромагнитного момента М
3
. В силу различных причин текущее значение
момента М(t) может отличаться от заданного М
3
. Тогда задача управления будет состоять в обеспечении
минимального значения функционала
()()
dttMMJ
t
t
∫
−=
0
2
3
или применительно к асинхронному электродвигателю
() () () ()()
dttttt
L
k
pMJ
t
t
rvsusvru
s
r
∫
ΨΨ−ΨΨ
′
−=
0
2
3
2
3
.
Таким образом, видим, что значение J зависит от характера изменения четырех функций, а фор-
мирование необходимого характера их изменения –задача управления состоянием электродвигателя.
46
Brachistochrone is Greek for "shortest time". The brachistochrone problem is to find the curve of the roller
coaster's track that will yield the shortest possible time for the ride. This problem was originally posed as a chal-
lenge to other mathematicians by John Bernoulli in 1696.
47
Иллюстрация импортирована с WEB-адреса http://galileo.imss.firenze.it/museo/a/ebrachi.html
