Еремин Е.Л., Еремина В.В., Капитонова М.С. Математическое и компьютерное моделирование

Подождите немного. Документ загружается.

в.

ЛАБОРАТОРНЫЕ РАБОТЫ

Перечень предлагаемых лабораторных работ включает в себя:

− Лабораторная абота №1 (4 ч.). Знакомство с рабочим местом лабо-

раторного комплекса.

− Лабораторная работа №2 (6 ч.). Имитационное моделирование пози-

ционных звеньев.

− Лабораторная работа №3 (4 ч.). Имитационное моделирование

интегрирующих звенье

− Лабораторная работа №4 (2 ч.). Имитационное моделирование ре-

ального дифференцирующего звена.

Выполнение всех заданий лабораторно практикума связано с ис-

пользованием MatLab – высокоэффективного программного обеспечения

для научных и инженерных расчетов.

6.1. ЛБ №1. Знакомство с рабочим местом лабораторного комплекса

Для вызова программной среды MatLab вам необходимо воспользо-

ваться кнопкой Пуск и выбрать следующую последовательность: Про-

граммы

→

MatLab for Windows

→

MatLab. После вызова MatLab на экра-

не появится окно, показанное на рис. 6.1

Рис. 6.1.

Из рис. 6.1 следует, что Рабочее место MatLab представляет собой

командное окно (MatLab Command Window), состоящее из:

главного меню, с разделами – File, Edit, Options, Windows, Help;

101

102

− рабочей области, с информационным текстом и специальным знаком

приглашения к работе “>>”, после которого вводится та или иная ко-

манда: demo, kmm и т.п.

Непосредственно для начала работы вводится команда kmm, в ре-

зультате чего в рабочей области MatLab Command Window появляется

диалоговое окно “Лабораторные работы по КММ” (рис. 6.2).

Рис. 6.2.

Представленное меню предлагает пользователю осуществить любое

из следующих действий:

− запустить интерактивный режим выполнения нужной лабораторной

работы;

− просмотреть пример заполнения отчета по лабораторной работе №1;

− просмотреть краткое описание программной среды MatLab;

− закрыть диалоговое окно.

Раздел меню “Краткое описание <PC-MatLab>” вызывает дополни-

тельное диалоговое окно, внешний вид которого приведен на рис. 6.3. С

помощью вызова этого дополнительного меню пользователь получает

доступ к соответствующим разделам справочного материала, в котором

кратко описаны наиболее характерные особенности применения и базо-

вые возможности программной среды MatLab.

Если в меню “Лабораторные работы по КММ” (см. рис. 6.2), вы-

брать и ввести раздел – Векторно-матричные преобразования пакета

MatLab, то это приведет к появлению в рабочей области MatLab

Command Window первоначального экранного фрагмента данной лабора-

103

торной работы (см. рис. 6.4), которую необходимо выполнить, внима-

тельно прочитав все указания, появляющиеся на экране.

Рис. 6.3.

Рис. 6.4.

Текст данной программы содержит наряду с краткими коммента-

риями и методическими указаниями, также и описание соответствующей

последовательности.

6. 2. ЛБ №2. Имитационное моделирование позиционных звеньев

Цель данной лабораторной работы – исследование динамических

характеристик группы позиционных звеньев (см. п. 3.1), в частности апе-

риодических 1-го и 2-го порядков и колебательного. Все эти звенья в

104

установившемся режиме описываются одинаковым уравнением вида (3.1)

и передаточными функциями вида (3.12) и (3.20) для апериодических

звеньев 1-го и 2-го порядка, соответственно, и (3.34) для колебательного

звена.

Требуется для динамических систем (3.12), (3.20) и (3.34) в соответ-

ствии с заданным вариантом (см. ниже) осуществить математическое и

имитационное моделирование (с построением графиков) следующих

временных и частотных характеристик:

h(t), w(t), A(

(

), U(

), V(

) и W(j

В качестве образца ниже приведена распечатка программы

, которая

будет отработана в диалоговом режиме после выбора пункта Характери-

стики апериодического звена 1-го порядка меню “Лабораторные работы

по КММ” и отражающая последовательность необходимых действий,

осуществляемых пакетом MatLab 4 для расчета и построения временных

и частотных характеристик апериодического звена 1-го порядка.

Ключевым моментом, от которого зависит правильность выполне-

ния данной и последующих лабораторных работ, является введение ко-

эффициентов числителя (num) и знаменателя (den) передаточной функ-

ции.

% АПЕРИОДИЧЕСКОЕ ЗВЕНО 1-ОГО ПОРЯДКА

% Рассматривается передаточная функция вида

% W (p) = x(p)/u(p) = K/(T*p + 1) (1)

% где x(p) и u(p) - изображения входа и выхода; К, Т - положительные постоянные коэффициенты.

% В А Р И А Н Т Ы:

% ¦No¦К ¦Т¦

% ¦==¦==¦=¦

% ¦01¦10¦1¦

% ¦02¦12¦2¦

% ¦03¦13¦3¦

% ¦04¦15¦1¦

% ¦05¦14¦3¦

% ¦06¦16¦2¦

% ¦07¦17¦1¦

% ¦08¦16¦2¦

% ¦09¦15¦3¦

% ¦10¦14¦2¦

% ВАШ вариант определяется последней цифрой номера в журнале

% (в соответствии со списком фамилий)

pause % Для продолжения работы нажмите любую клавишу ...

% ЗАДАНИЕ

% Требуется:

Это распечатка экранной формы окна управления MatLab 4, полученная при выполнении расчетов с кон-

кретными данными.

105

% 1. Построить переходной процесс, весовую функцию.

% 2. Построить АЧХ, ФЧХ, ВЧХ, МЧХ, АФЧХ.

% Введите числитель (num) передаточной функции (1).

num = input('num=')

num=[14]

num =

pause % Для продолжения работы нажмите любую клавишу ...

% Введите знаменатель (den) передаточной функции (1).

den = input('den=')

den=[3 1]

den =

3 1

pause % Для продолжения работы нажмите любую клавишу ...

% Переход в пространство состояний

pause % Для продолжения работы нажмите любую клавишу ...

[a,b,c,d] = tf2ss(num,den)

a =

-0.3333

b =

c =

4.6667

d =

pause % Для продолжения работы нажмите любую клавишу ...

% Построение переходного процесса

t=0:.005:15;

step(a,b,c,d,1,t);

pause % Для продолжения работы нажмите любую клавишу ...

% Построение весовой функции

impulse(a,b,c,d,1,t);

pause % Для продолжения работы нажмите любую клавишу ...

% Построение частотных характеристик

106

w=0:.005:30;

[mag,phase] = bode(a,b,c,d,1,w);

[re,im] = nyquist(a,b,c,d,1,w);

pause % Для продолжения работы нажмите любую клавишу ...

subplot(221), plot(w,mag), title('Magnitude response'), xlabel('Radians/s'),

subplot(223), plot(w,phase), title('Phase response'), xlabel('Radians/s'),

subplot(222), plot(w,re), title('Real response'), xlabel('Radians/s'),

subplot(224), plot(w,im), title('Image response'), xlabel('Radians/s'),

pause % Для продолжения работы нажмите любую клавишу ...

plot(re,im), title('W(jw)'), xlabel('Re'), ylabel('Im'),

pause % Для завершения работы нажмите любую клавишу ...

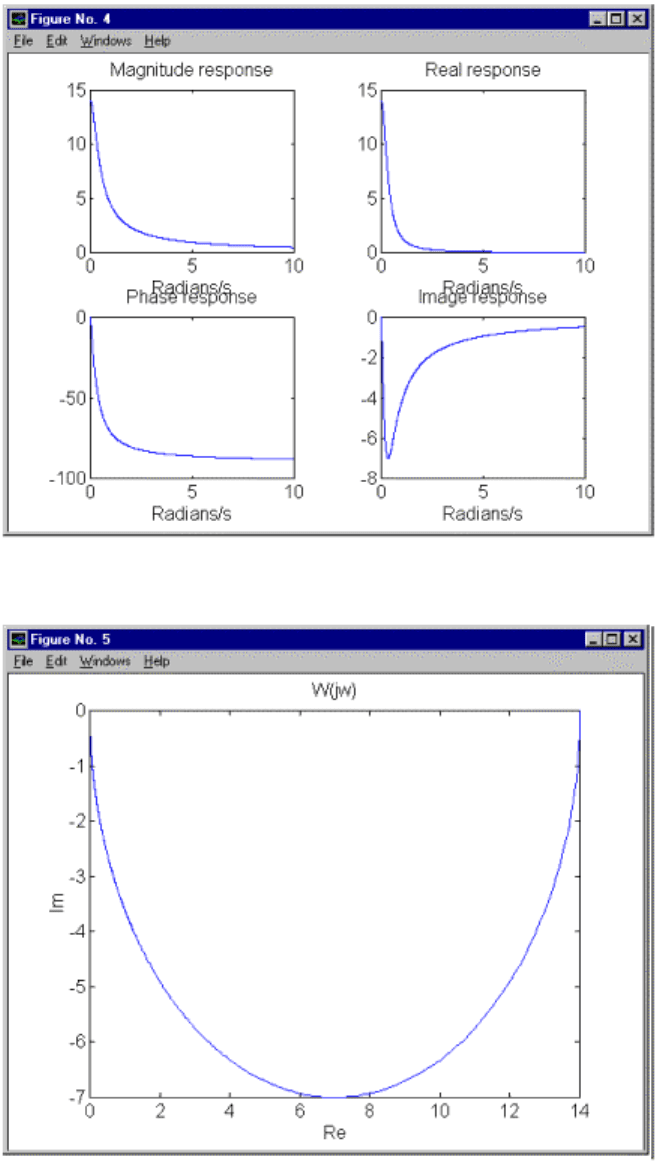
Реализации данной программы в графических образах показана на

рис. 6.5 – 6.8: рис. 6.5 – переходный процесс; рис. 6.6 – весовая функция;

рис. 6.7 – частотные характеристики A(

(

), U(

), V(

); рис. 6.8 – го-

дограф W(j

Для того чтобы в процессе выполнения программы каждый рисунок

появлялся в отдельном окне, необходимо в появившемся графическом

окне выбрать меню File команду New Figure.

Для сохранения графических образов можно использовать в меню

Edit команду Copy to bitmap. Затем нужно открыть графический редактор

Paint, создать в нем новый файл и вставить рисунок, выбрав команду

главного меню Правка

→

Вставить. Теперь рисунок можно отредакти-

ровать (например, обратить цвета) и сохранить, выбрав команду Сохра-

нить или Сохранить как… в меню Файл.

Для исследования апериодического звена 2-го порядка и колеба-

тельного звена выбираются пункты, соответственно, Характеристики

апериодического звена 2-го порядка и Характеристики колебательного

звена, вследствие чего будет отработана аналогичная программа.

АПЕРИОДИЧЕСКОЕ ЗВЕНО 2-ОГО ПОРЯДКА

% В А Р И А Н Т Ы:

% ¦No¦К ¦Т1¦Т2¦

% ¦01¦10¦ 1¦10¦

% ¦02¦12¦ 2¦11¦

% ¦03¦13¦ 3¦12¦

% ¦04¦15¦ 1¦13¦

% ¦05¦14¦ 3¦14¦

% ¦06¦16¦ 2¦15¦

% ¦07¦17¦ 1¦14¦

% ¦08¦16¦ 2¦13¦

% ¦09¦15¦ 3¦12¦

% ¦10¦14¦ 2¦11¦

КОЛЕБАТЕЛЬНОЕ ЗВЕНО

% В А Р И А Н Т Ы:

% ¦No¦К ¦Т1¦Т2¦

% ¦01¦10¦11¦3¦

% ¦02¦12¦12¦2¦

% ¦03¦13¦13¦1¦

% ¦04¦15¦11¦1¦

% ¦05¦14¦13¦2¦

% ¦06¦16¦12¦2¦

% ¦07¦17¦11¦3¦

% ¦08¦16¦12¦3¦

% ¦09¦15¦13¦1¦

% ¦10¦14¦12¦1¦

Результаты выполненной лабораторной работы предоставляются в

виде отчета, в котором необходимо записать: дифференциальное уравне-

107

ние звена, вид передаточной функции, уравнения временных характери-

стик h(t) и w(t) с соответствующими графиками, уравнения частотных ха-

рактеристик W(j

) и A(

(

), U(

), V(

) с их графиками. Для подго-

товки отчета рекомендуется использовать текстовый редактор MS Word.

Рис. 6.5.

Рис. 6.6.

108

Рис. 6.7.

Рис. 6.8.

6. 3. ЛБ №3. Имитационное моделирование интегрирующих звеньев

Цель работы – исследование динамических характеристик идеаль-

ного интегрирующего звена и интегрирующего звена с замедлением (см.

п. 3.2). Эти звенья в установившемся режиме описываются одинаковым

109

уравнением вида (3.43) и передаточными функциями вида (3.45) и (3.54),

соответственно.

Требуется для динамических систем (3.45) и (3.54) в соответствии с

заданным вариантом осуществить математическое и имитационное моде-

лирование (с построением графиков) следующих временных и частотных

характеристик:

h(t), w(t), A(

(

), U(

), V(

) и W(j

Для выполнения данной лабораторной работы выбираются в меню

“Лабораторные работы по КММ” пункты

Характеристики идеального интегрирующего звена и

Характеристики интегрирующего звена с замедлением, вследствие

чего будет отработана последовательность действий, осуществляемых

пакетом MatLab 4 для расчета и построения временных и частотных ха-

рактеристик (программа аналогична описанной в п. 6.2).

ИДЕАЛЬНОЕ ИНТЕГРИРУЮЩЕЕ ЗВЕНО

% В А Р И А Н Т Ы:

% ¦No¦К ¦

% ¦==¦==¦

% ¦01¦10¦

% ¦02¦22¦

% ¦03¦13¦

% ¦04¦25¦

% ¦05¦14¦

% ¦06¦26¦

% ¦07¦17¦

% ¦08¦26¦

% ¦09¦15¦

% ¦10¦24¦

ИНТЕГРИРУЮЩЕЕ ЗВЕНО С ЗАМЕДЛЕНИЕМ

% В А Р И А Н Т Ы:

% ¦No¦К ¦Т¦

% ¦==¦==¦=¦

% ¦01¦10¦1¦

% ¦02¦12¦2¦

% ¦03¦13¦3¦

% ¦04¦15¦1¦

% ¦05¦14¦3¦

% ¦06¦16¦2¦

% ¦07¦17¦1¦

% ¦08¦16¦2¦

% ¦09¦15¦3¦

% ¦10¦14¦2¦

Результаты выполненной лабораторной работы предоставляются в

виде отчета, в котором необходимо записать: дифференциальное уравне-

ние звена, вид передаточной функции, уравнения временных характери-

стик h(t) и w(t) с соответствующими графиками, уравнения частотных ха-

рактеристик W(j

) и A(

(

), U(

), V(

) с их графиками. Для подго-

товки отчета рекомендуется использовать текстовый редактор MS Word.

6. 4. ЛБ №4. Имитационное моделирование

реального дифференцирующего звена

Цель работы – исследование динамических характеристик реально-

го дифференцирующего звена (см. п. 3.3). Это звено в установившемся

110

режиме описывается уравнением вида (3.71) и передаточной функцией

(3.72).

Требуется для процесса (3.71) в соответствии с заданным вариантом

осуществить математическое и имитационное моделирование (с построе-

нием графиков) следующих временных и частотных характеристик:

h(t), w(t), A(

(

), U(

), V(

) и W(j

Для выполнения данной лабораторной работы выбираются пункты,

соответственно, Характеристики реального дифференцирующего звена,

вследствие чего будет отработана последовательность действий, осуще-

ствляемых пакетом MatLab4 для расчета и построения временных и час-

тотных характеристик.

РЕАЛЬНОЕ ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО

% В А Р И А Н Т Ы:

% ¦No¦К ¦Т¦

% ¦==¦==¦=¦

% ¦01¦10¦1¦

% ¦02¦12¦2¦

% ¦03¦13¦3¦

% ¦04¦15¦1¦

% ¦05¦14¦3¦

% ¦06¦16¦2¦

% ¦07¦17¦1¦

% ¦08¦16¦2¦

% ¦09¦15¦3¦

% ¦10¦14¦2¦

Результаты выполненной лабораторной работы предоставляются в

виде отчета, в котором необходимо записать: дифференциальное уравне-

ние звена, вид передаточной функции, уравнения временных характери-

стик h(t) и w(t) с соответствующими графиками, уравнения частотных ха-

рактеристик W(j

) и A(

(

), U(

), V(

) с их графиками. Для подго-

товки отчета рекомендуется использовать текстовый редактор MS Word.