Еремин Е.Л., Еремина В.В., Капитонова М.С. Математическое и компьютерное моделирование
Подождите немного. Документ загружается.

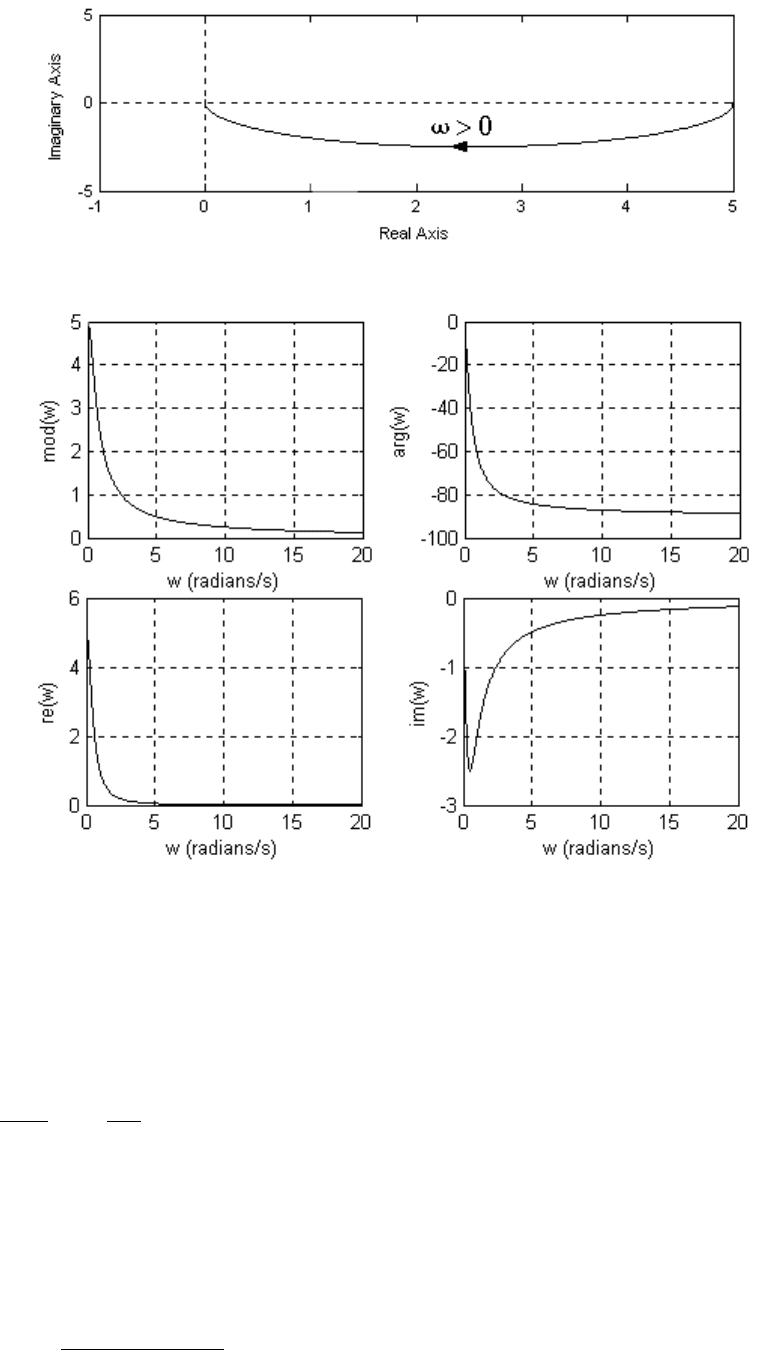
Рис. 3.7.
Рис. 3.8.
3.1.3. Инерционное звено 2-го порядка
Инерционное или апериодическое звено 2-го порядка описывают
уравнением
kux
d
t
dx
T
d
t
xd
T
=++
2
2
2
2
1
, T , (3.19)
2
1
2
2
4T>
где положительные числа k – коэффициент передачи; T
1
2
, T
2
– постоян-
ные времени. Часто вместо T
1
2
пишут просто T
1
, что означает лишь изме-
нение обозначения, но сохранение размерности, т.е. здесь T
1
в [сек]
2
.
Уравнению (3.19) соответствует передаточная функция
1
)(
2
2
2
1
++
=
sTsT
k
sW
. (3.20)
Поскольку при T
2
2
>4T
1
2
корни характеристического уравнения
01
2
2
2
1
=++ sTsT
61
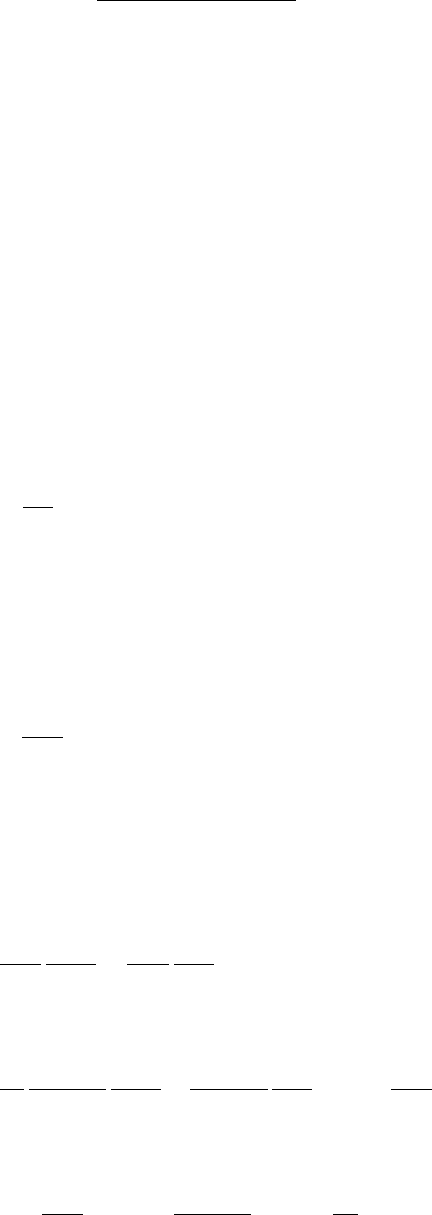
всегда будут вещественными, то передаточную функцию (3.20) удобно
записывать следующим образом:
)1)(1(
)(
43
++
=
sTsT
k
sW
, (3.21)
т.е. рассматривая новые постоянные времени
=+
=
∆
∆
.
,
243
2
143
TTT
TTT
В качестве примера математического описания инерционного звена
2-го порядка рассмотрим уравнения электродвигателя постоянного тока с
независимым возбуждением, схема которого изображена на рис. 3.5b.
Известно, что с учетом электромагнитной реакции цепи якоря, но при от-
сутствии момента нагрузки на валу двигателя, динамику последнего опи-
сывают двумя уравнениями:
во-первых – уравнением равновесия ЭДС в якорной цепи
υ
Eвх
KuRi
d
t
di
L −=+
, (3.22)
где L, R – соответственно индуктивность и активное сопротивление якор-
ной цепи, а K
E
– коэффициент пропорциональности между обратной ЭДС
и скоростью вращения двигателя υ;
во-вторых – уравнением равновесия моментов на валу двигателя
iK
d
t
d
J
м
=
ν
, (3.23)
где K
М
– коэффициент пропорциональности между вращающим момен-
том и током якоря i.
Исключив в уравнениях (3.22), (3.23) промежуточную переменную i,
можно записать следующее уравнение движения электродвигателя
вхE
мм
uK
dt
d
K
RJ
dt
d
K
LJ
=++
υ
υ
υ
2
2
,
которому в первой форме записи будет соответствовать выражение
вх
EEмEм
u
Kdt
d
KK
RJ
dt
d
KK
RJ
R
L 1
2
2
=++
υ
υ
υ
. (3.24)
Если ввести обозначения
,,
1
Eм
M
E
KK
RJ
T
K
k
∆∆
==
,
R
L
Я
∆
=
T
x = υ, u = u
вх
,
где Т
М
– электромеханическая постоянная времени двигателя, а Т
Я
– ее
электромагнитная постоянная, то уравнение (3.24) получит вид
62

kux
d
t
dx
T
d
t
xd
TT
MЯM
=++
2
2
. (3.25)
Уравнение (4.24) будет полностью эквивалентно уравнению (3.12) только
при выполнении дополнительного коэффициентного соотношения
04
2
>−
ямм
TTT или T . (3.26) 04 >>
ям
T
Другие примеры инерционного 2-го звена показаны на рис. 3.9, где
каждое представляет собой последовательное соединение двух инерци-
онных звеньев 1-го порядка (см. рис. 3.5).
Рис. 3.9.
Поскольку у передаточной функции вида (3.21) корни характери-
стического уравнения имеют вещественные значения
3
1
1
T
s −=
,
4
2
1
T
s −=
,
то переходной процесс будет описываться следующим образом:
,1
))((
/
)(
4
3
43
4
43
3
21
43
1
−
+
−
−=
=
−−
=
−
−
−
T
t
T
t
e
TT
T
e
TT
T
k
sssss
TTk
Lth
(3.27)
а импульсной переходной характеристике будет соответствовать уравне-
ние
−
−
=
−
−
4
3
43
)(
T
t
T
t
ee
TT
k
t
ω
. (3.28)
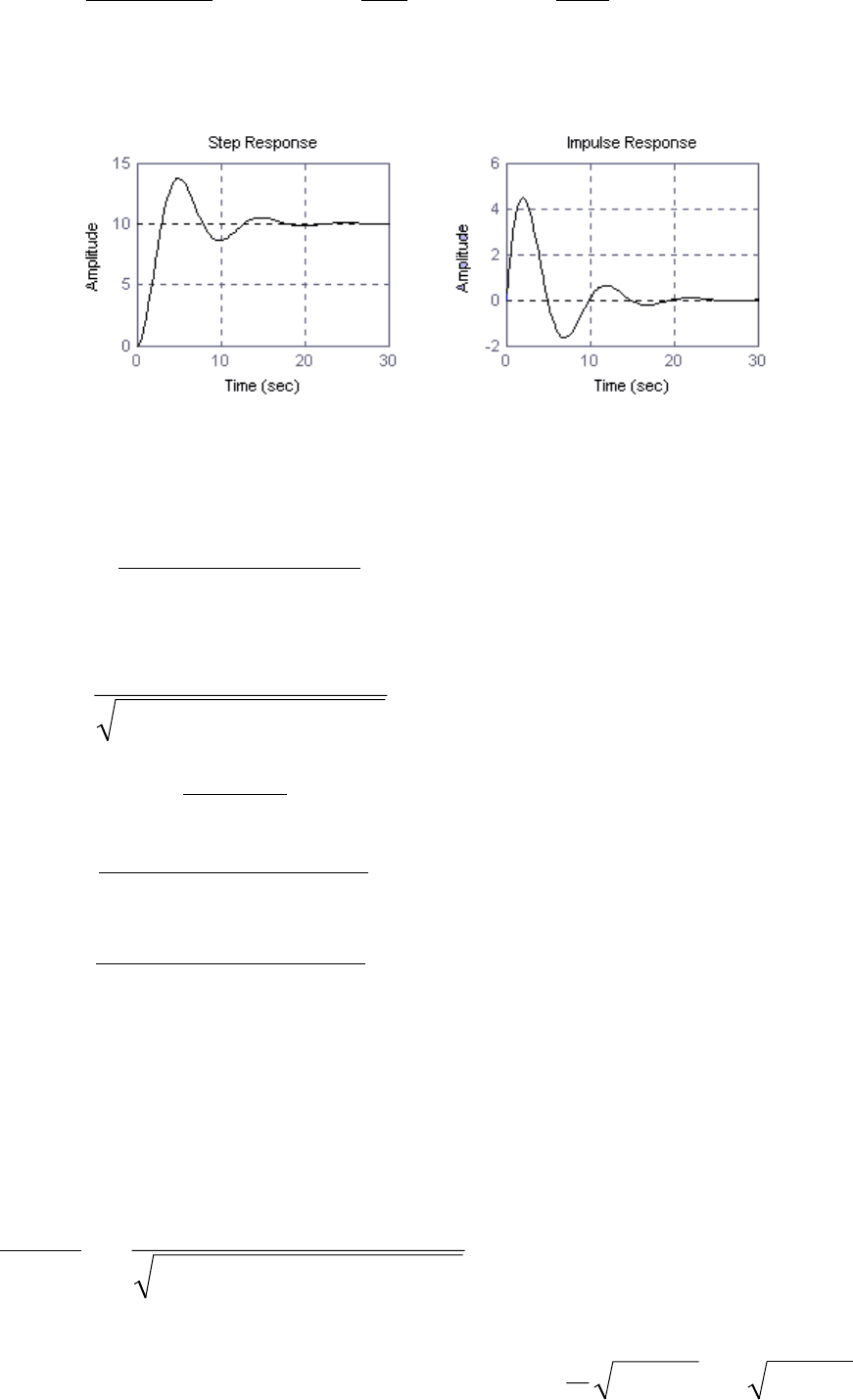
Графики временных характеристик инерционного звена 2-порядка
со значениями коэффициентов
63

k = 5, T
3
= 1, T
4
= 3, (3.29)
представлены на рис. 3.10.
Рис. 3.10.
Частотная передаточная функция, получаемая из (3.21), имеет вид
)1)(1(
)(
43
TjTj
k
jW
ωω
ω
++
=
. (3.30)
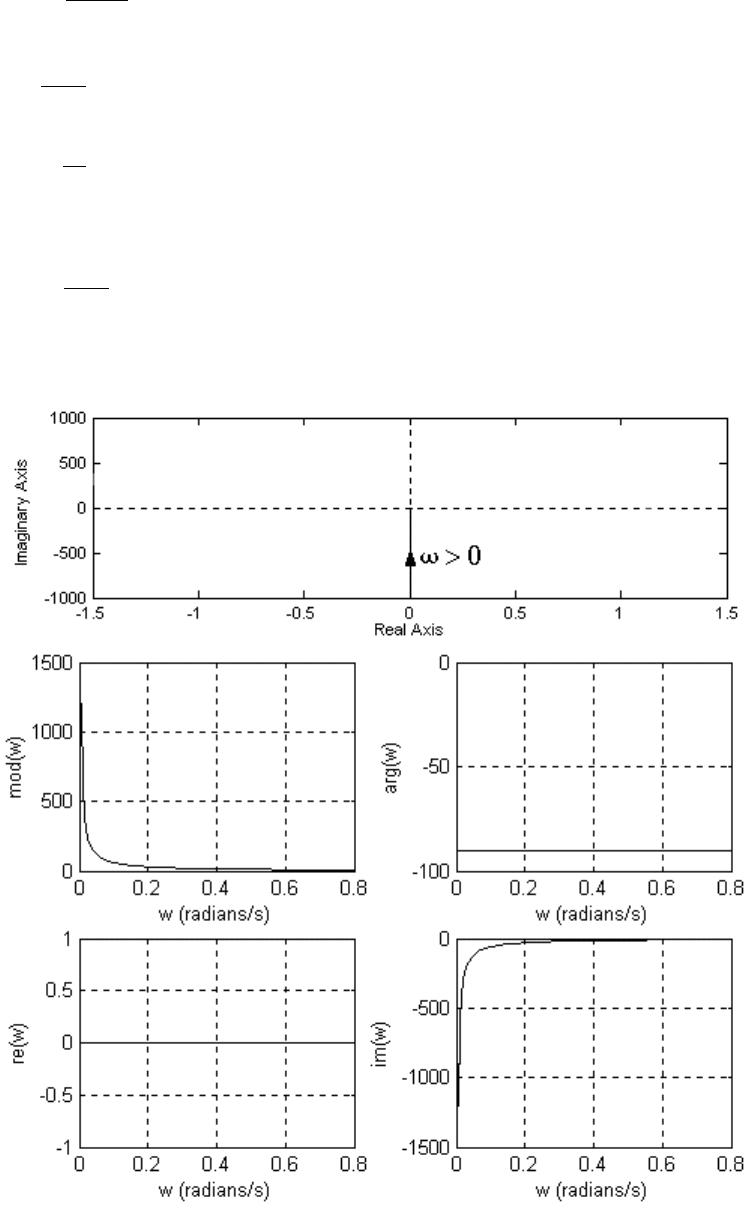
Годограф функции (3.30) со значениями (3.29) показан на рис. 3.11.
Рис. 3.11.
Амплитудная и фазовая частотные характеристики, как следует из
соотношения (3.30), описываются соотношениями
,)(
,
)1)(1(
)(
43
2
4
2
2
3
2
TarctgTarctg
TT
k
A
ωωωϕ
ωω
ω
−−=
++
=
(3.31)
а вещественная и мнимая частотные характеристики, также получаемые
из (3.30), имеют вид
4
.
)1)(1(
)(
)(
,
)1)(1(
1
)(
2
4
2
2
3
2
43
2
4
2
2
3
2
43
2
TT
TT
V
TT
TT
U
ωω
ω
ω
ωω
ω
ω
++
+−
=
++
−
=
(3.32)
Графики частотных характеристик (3.31), (3.32) со значениями ко-
эффициентов (3.29), приведены на рис. 3.12.
64
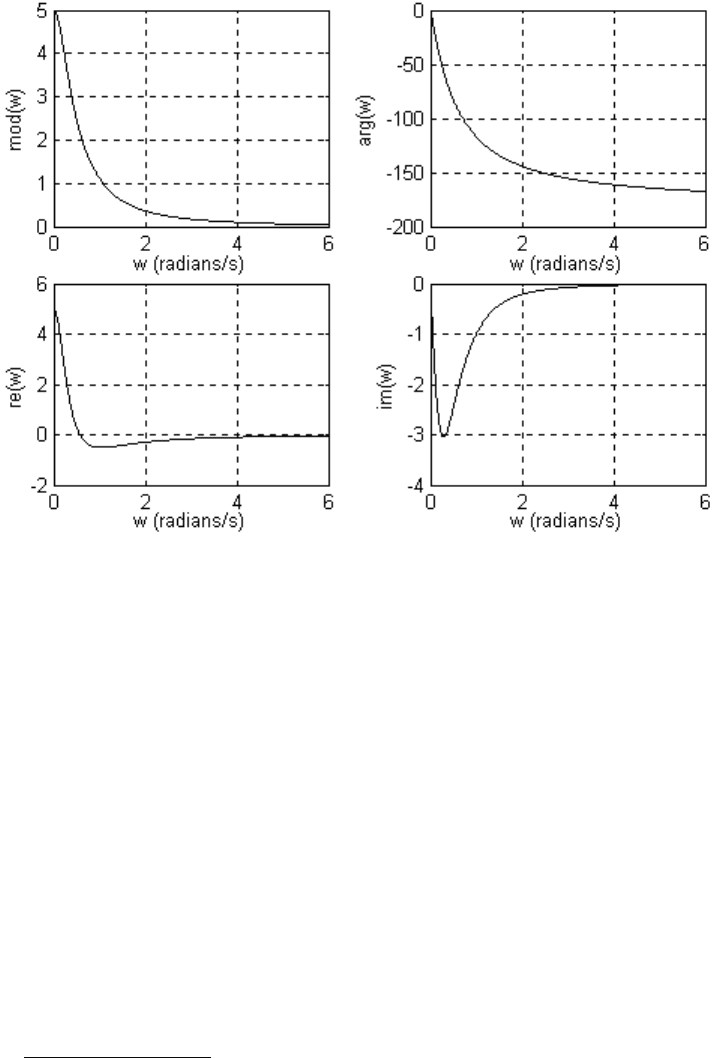
Рис. 4.12.
3.1.4. Колебательное звено
Как и апериодическое звено 2-го порядка, колебательное также опи-
сывается дифференциальным уравнением вида (3.19), но при этом ука-
занное в (3.19) неравенство заменяется на противоположное, т.е. получа-
ет вид
2
1
2
2
4TT < . (3.33)
Очевидно, что при этом оба корни характеристического уравнения пере-
даточной функции (3.20) оказываются комплексно-сопряженными. В
этом случае передаточную функцию (3.20) удобно записывать следую-
щим образом:
12
)(
22
++
=
TssT
k
sW
ξ
, (3.34)
т.е. рассматривая новые коэффициенты, определяемые из соотношений
=
=
∆
∆
,2
,
2
2
1
2
TT
TT
ξ
где
ξ
– коэффициент затухания 0 ≤
ξ
< 1; T – постоянная времени, удов-
летворяющая соотношению q = T
-1
, здесь q – угловая частота свободных
колебаний при отсутствии затухания, т.е. при
ξ
= 0.
Примером конкретного математического описания колебательного
звена может служить уравнение двигателя постоянного тока с независи-
мым возбуждением вида (3.25), но только в том случае, когда его пара-
65
метры удовлетворяют неравенству T . 04
2
<−
ямм
TT
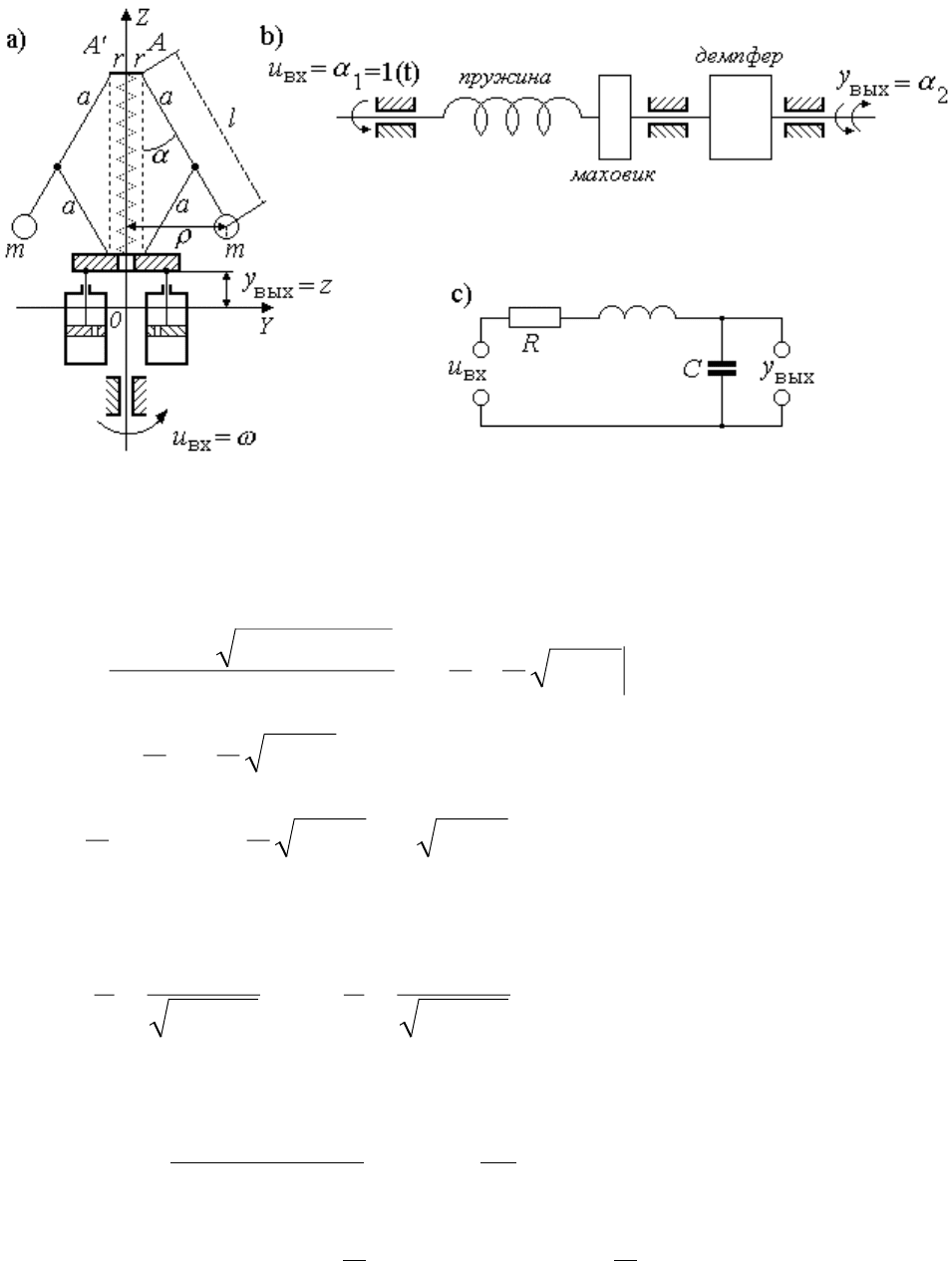
Примеры колебательного звена представлены на рис. 3.13: а) цен-
тробежный маятник; b) механическая система; с) RLC-цепочка.
Рис. 3.13.
Если определить корни характеристического уравнения
012
22
=
++ TssT
ξ
и записать их в виде
,11
1
,
,1
1
1
1
2
442
22
2
1
2
2
222
2,1
2
ξξλξ
ξ
γ
λγξ
ξ
ξ
ξ
ξξ
ξ
−=−===
±−=−±−=
=−±−=
−±−
=
∆∆
<
q
T
q
T
j
T
j
T
TTT
TTT
s
(3.35)
то из двух последних уравнений можно установить зависимость коэффи-
циентов T,
ξ
(или q,
ξ
) от параметров γ и λ, в виде следующих функций:
,,
11
2222
γλ
γ
γ
ξ
γλ
+
==
+
==
qq
T
Переходной процесс и импульсная переходная характеристика ко-
лебательного звена описываются соотношениями
,,)sin(cos1
)sin(1
))((
/
)(
21
2
1
γ
λ
ϕλ
λ
γ
λ
ϕλ
ξλ
γ
γ
γ
arctgttek
tek
sssss
Tk
Lth
t
t
∆
−
−−
=
+−=
=
+−=
−−
=
(3.36)
66
()
,sinsinsin)(
2
2222
te
k
te
kq
te
k
t
ttt
λ
λξ
γ
λ
λ
λ
λ
λ
γ
ω
γγγ
−−−
==
+
=
(3.37)
а их графики, построенные при значении коэффициентов k = 10, T =
1.5,
ξ
= 0.3, показаны на рис. 3.14.
Рис. 3.14.
Частотная передаточная функция, согласно уравнению (3.34), опи-
сывается выражением вида
()
TjT
k
jW
ξωω
ω
21
)(
22
+−
=
(3.38)
а частотные характеристики следующим образом:
()
222
2
22
41
)(
TT
k
A
ωξω
ω
+−
=
, (3.39)
22
1
2
)(
ω
ξω
ωϕ
T
T
arctg
−
−= (3.40)
()
()
222
2
22
22
41
1
)(
TT
Tk
U
ωξω
ω
ω
+−
−
=
, (3.41)
()
.
41
2
)(
222
2
22
TT
Tk
V
ωξω
ξω
ω
+−
−
=
(3.42)
Известно, что в колебательном звене может появиться резонанс, ко-
гда в некотором частотном диапазоне текущее значение амплитуды пре-
вышает величину А(0), а при резонансной частоте
ω
рез
достигает своего
максимума, т.е. А(
ω
рез
) = max А(
ω
). Определить величину
ω
рез
можно, на-
пример, используя необходимое условие экстремума функции
()
()
0
4)1(
212)(
3
222222
222
=
+−
+
+−−
==
∂
∂
ωξω
ξ
ω
ω
ω
ω
TT
TkTA
.
Поскольку при
ω
= 0 резонанса быть не может, то величину
ω
рез
находят
из условия
021
222
=++−
ξ
ω
T , в виде
22
2121
1
ξξω
−=−= q
T
рез
, где
67

рассматриваются лишь вещественные значения
ω
рез
, удовлетворяющие
неравенству
1 02
2
>−
ξ
, при этом коэффициентное соотношение
ξ
< 0.707
– это условие наличия резонанса.
,)(
0
kdttu
t
∫
Годографы частотной передаточной функции, построенные со зна-
чениями коэффициентов k = 10, T = 1.5, при
ξ
= 0.3 и
ξ
= 0.5, показаны на
рис. 3.15, а графики частотных характеристик – на рис. 3.16.
Рис. 3.15.
Рис. 3.16.
3.2. Группа интегрирующих звеньев
К этой группе звеньев обычно относят интегрирующее звено и ин-
тегрирующее звено с замедлением. Эти звенья в установившемся режиме
описываются одним и тем же уравнением
.)( constktx ==
(3.43)
3.2.1. Интегрирующее звено
Звено иногда называют идеально интегрирующим, тем самым под-
черкивая, что для любого момента времени его математической моделью
68

является уравнение (3.43), которое можно переписать и в дифференци-
альной форме
ku
d
t
dx
=
или u
d
t
dx
=T
, где )с(
1
k
T . (3.44) =
Примеры физической реализации интегрирующего звена показаны
на рис. 3.17: а) интегратор на операционном усилителе; b) гидравличе-
ский демпфер, динамика которого (без учета инерции) описывается соот-
ношением
s
K
p
dt
dx
==
ν
, где K
s
– коэффициент скоростного сопротивле-
ния.
Рис. 3.17.
В соответствии с уравнениями (3.44), передаточная функция интег-
рирующего звена имеет вид
s
k
Ts
sW ==
1
)(
, (3.45)
следовательно, переходной процесс и импульсная переходная характери-
стики описываются соотношениями
kt
s
k
Lth =
=
−
2
1
)( , (3.46)
k
d
t
tdh
t ==
)(
)(
ω
. (3.47)
Графики временные характеристик интегрирующего звена, постро-
енные при значении параметра k = 6, изображены на рис. 3.18.
Рис. 3.18.
Частотная передаточная функция и частотные характеристики име-
69
ют вид
,
1
)(
Tj
jW
ω
ω
= (3.48)
T
A
ω
ω
1
)( =
, (3.49)
2
)(
π
ωϕ
−= , (3.50)
,0)( =
ω
U (3.51)
,
1
)(
T
V
ω
ω
−= (3.52)
графики которых, построенные при значении параметра Т = 1/6, показаны
на рис. 3.19
Рис. 3.19
3.2.2. Интегрирующее звено с замедлением
Звено описывается уравнением
70
