Еремин Е.Л., Еремина В.В., Капитонова М.С. Математическое и компьютерное моделирование
Подождите немного. Документ загружается.

у
2
(t)}∈ .
21
ll
R
+
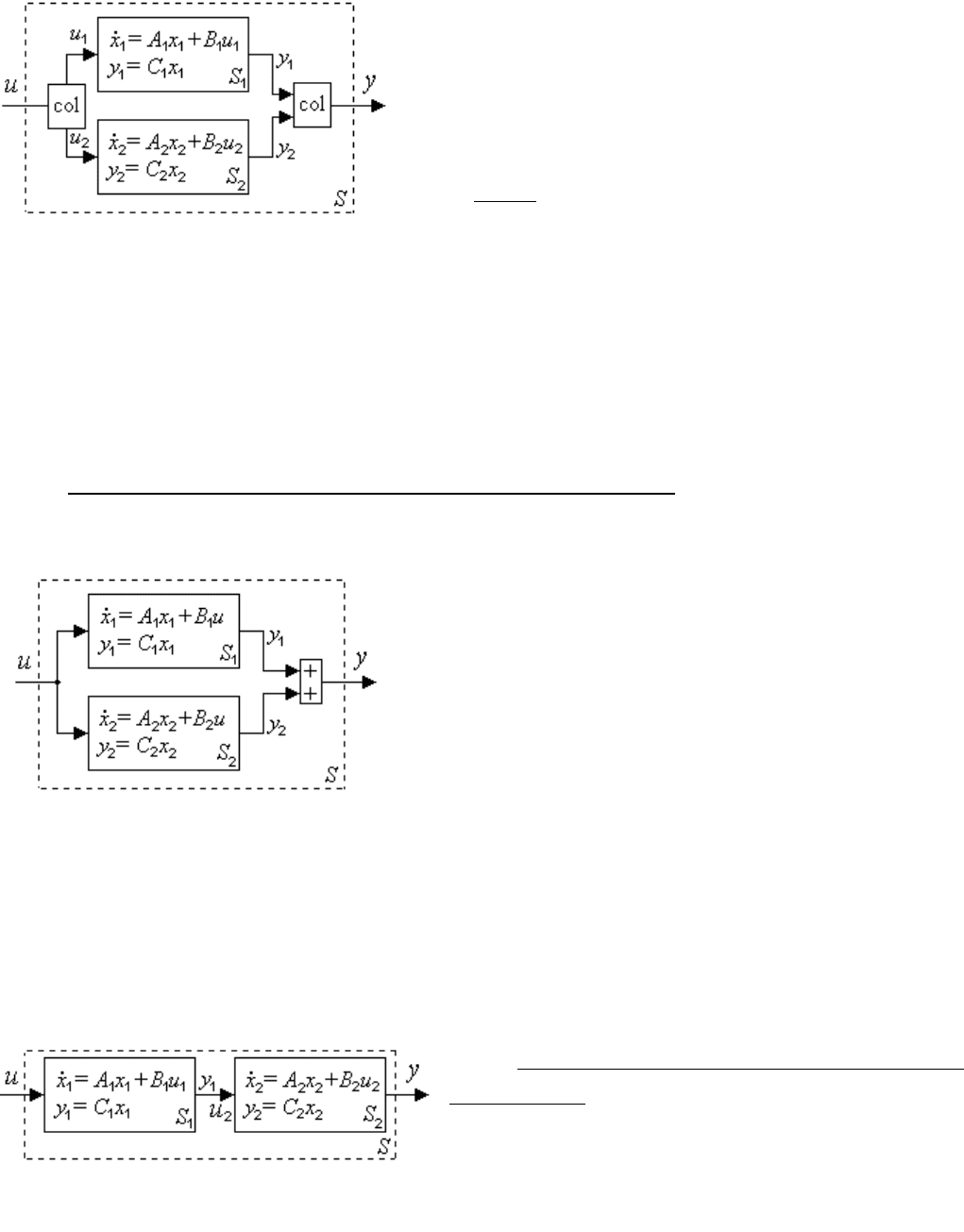
Графический образ объеди-
нения систем S
i
в одну показан на рис.
2.13, математическое описание которого
представляет собой систему уравнений
)(
)(
Cxty
dt
tdx
=
=
0
1
C
()
.
2
C
Рис. 2.13. Модель объединения
независимых систем (2.70).
),(
),()(
t
tButAx +
(2.71)
где блочные матрицы А, B, С имеют следующую структуру:
,
0
0
2
1
=
A
A
A
.
0
,
0
0
22
1
=
=
C
C
B
B
B
Параллельное соединение систем (подсистем). Принципиальное от-
личие параллельного соединения двух подсистем от объединения двух
независимых систем состоит в том, что при параллельном соединении
вход и(t) = и
1
(t) = и
2
(t) поступает на обе
подсистемы одновременно, а выход этого
соединения образуется как сумма у(t) =
у
1
(t) + у
2
(t) (рис. 2.14). Вектор состояния
x(t) остается по-прежнему составным и
имеет вид x(t) = col{x
1
(t), x
2
(t)}∈ .
21
nn
R
+
Математическое описание сис-
темы S, образованной параллельным со-
единением нескольких систем S
i
, имеет по-
прежнему вид (2.71), где матрицы А, B, С также блочные, вида
Рис. 2.14. Модель параллельного
соединения двух систем.
,,
0
0
1
2
1
2
1
CC
B
B
B
A
A
A =
=
=
Последовательное соединение
подсистем, (рис. 2.15), где входом сис-
темы S является вход подсистемы S
1
,
и(t) = и
1
(t), а выход системы S форми-
руется
выходом второй подсистемы S
2
,
у(t) = у
2
(t). При этом выход первой
подсистемы является входом второй, и
2
(t) = у
1
(t), поскольку их размерно-
сти совпадают. Описывая систему, представленную на рис. 2.15 уравне-
ниями (2.71), получаем следующие блочные матрицы:
Рис. 2.15. Последовательное
соединение двух подсистем.
41

()
.0,
0
,
0
2
1
212
1
CC
B
B
ACB
A
A =
=
=
Соединение подсистем с обратной
связью, (рис. 2.16), где выход подсистемы
S
2
вычитается (при положительной обрат-
ной связи прибавляется) из входа всей сис-
темы S и поступает на вход подсистемы S
1
.
Другими словами, и
1
(t) = и(t) – у
2
(t), и
2
(t) =
у
1
(t), что позволяет в математическом опи-
сании (2.71) для системы, показанной на
рис. 2.16, получить блочные матрицы вида
Рис. 2.16. Соединение подсистем
c обратной связью.
()
.0,
0
,
1
1
212
211
CC
B
B
ACB
CBA
A =
=
−
=
2.3. Дискретизация непрерывных моделей
2.3.1. Решение уравнений состояния
Пусть исследуемая система линейна и не содержит нестационарных
элементов, т.е. уравнения динамики имеют вид
),()(
)(
tButAx
d
t
tdx
+=
(2.72)
),()()(
t
Du
t
Cx
t
y += (2.73)
где x(t)∈R
n
; u(t)∈R
m
; y(t)∈R
l
. Очевидно, что если функция x(t) определена,
то выход y(t) вычисляется непосредственно из (2.73).
Рассмотрим решение задачи Коши, т.е. определим вектор состояния
x(t) при известном
начальном значении х(0) и заданном входном процессе
и(t).
Решение однородного уравнения
)(
)(
tAx
d
t
tdx
=
(2.74)
для всех действительных t
0
, при выполнении равенства
,),(Ф),,(Ф
),(Ф
000
0
EttttA
d
t
ttd
==
(2.75)
42

где x(t)∈R
n
; Ф(t, t
0
) = X(t)Х
-1
(t
0
) – переходная матрица состояния; X(t) –
фундаментальная матрица-функция, можно представить в виде
).(),(Ф)(
00
txtttx = (2.76)
Для того, чтобы воспользоваться выражением (2.76), необходимо
уметь вычислять матрицу Ф(t, t
0
). Известно, что поскольку уравнение
(2.74) стационарное, то матрица Ф(t, t
0
) зависит от одного аргумента
θ
и
совпадает с матричной экспонентой Ф(t, t
0
) = е
А
θ
,
θ
= t – t
0
, которую мож-
но определить в виде ряда
.
!
)(
...
!
)(
...
2
)(
1
2
∑
∞
=
+=++++++=
k
kk
A
k
A
E
k
AA
AEe
θθθ
θ
θ
(2.77)
Таким образом, решение уравнения (2.74) определяется формулой
,)(
0
xetx
At
=
(2.78)
где х
0
= х(t
0
=0). Выражение (2.78) имеет наиболее простой вид тогда, ко-
гда матрица А = diag{s
1
, s
2
, …, s
n
}, поскольку матрица e
At
также будет
диагональной
{
}
ts
tsts
At
n
eeee ...diag
21
= .
Решение неоднородного уравнения (2.72) можно представить в виде
),()()( txtxtx
частобщ
+=
где x
общ
(t) – переходная составляющая или общее решение однородного
уравнения (2.74) при заданных начальных условиях; x
част
(t) – вынужден-
ная составляющая или частное решение уравнения (2.72) при нулевых
начальных условиях.
Как известно, x
общ
(t) имеет вид
∫
=
t
t
общ
dButtx
0
,)(),(Ф)(
ϑϑϑ
а x
част
(t) представляет собой выражение (2.76); следовательно, для x(t)
можно записать следующую формулу Коши
,)(),(Ф),(Ф)(
0
00
∫
+=
t
t
dButxtttx
ϑϑϑ
(2.79)
а для стационарных систем в силу Ф(t, t
0
) = е
А
θ
,
θ
= t – t
0
выражение (2.79)
представить в виде
43
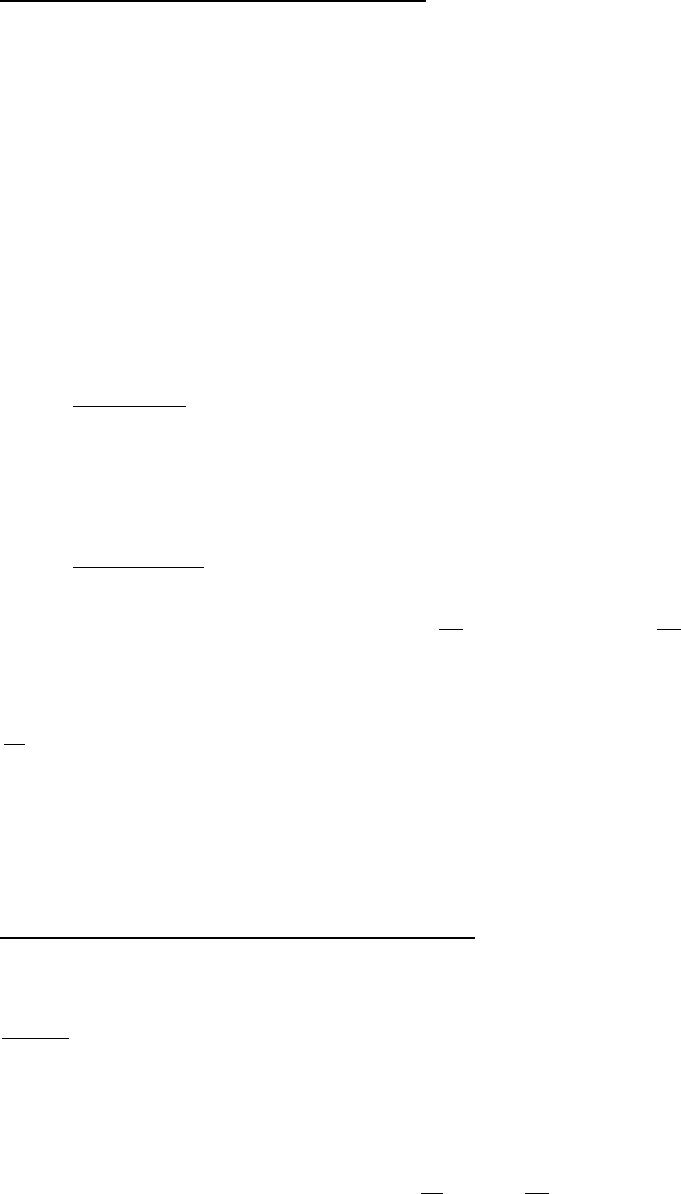
()
()
,)()(
0
0
0
∫
−
−
+=
t
t
tA
ttA
dBuexetx
ϑϑ
ϑ
(2.80)
часто называемом переходным уравнением состояния.
Свойства переходной матрицы
. Перечислим основные свойства мат-
рицы Ф(t, t
0
).
1. ∀t
0
имеет место Ф(t
0
, t
0
) = E.
2. ∀t
0
, t
1
, t выполнено правило композиции
Ф(t, t
0
) = Ф(t, t
1
)Ф(t
1
, t
0
).
3. det Ф(t, t
0
) ≠ 0 ∀t
0
, t.
4. Ф(t, t
0
) = X(t)Х
-1
(t
0
) , где X(t) – любая фундаментальная матрица.
5. (Ф(t, t
0
))
-1
= Ф(t
0
, t) ∀t
0
, t.
6. Справедливо уравнение
.),(),,()(
),(
000
0
EttФttФtA
d
t
ttdФ
==
7. Матрица Ф
T
(t, t
0
) удовлетворяет сопряженному уравнению
.),(),,()(
),(
000
0
EttФttФtA
d
t
ttdФ
TT
T
=−=
8. Если det T ≠ 0, Ф
T
(t, t
0
) = Т
-1
Ф
T
(t, t
0
)Т, где Ф (t, t
0
) удовлетворя-
ет
(2.75), в котором вместо матрицы А подставлена подобная ей мат-
рица
A
(t) = ТA(t)Т
-1
.
2.3.2. Дискретные модели непрерывных систем
Постановка задачи дискретизации
. Для динамической системы, не-
прерывная модель которой имеет вид
,),()()(),()(
)(
RttDutCxtytButAx
d
t
tdx
∈+=+= (2.81)
требуется получить эквивалентную систему разностных уравнений или ее
дискретную модель вида
.,...1,0],[][][],[][]1[ =+=+=+ kkuDkxCkykQukPxkx (2.82)
Здесь под эквивалентностью систем понимается совпадение их ре-
44

акций на одно и то же входное воздействие при соответствующих на-
чальных условиях. Более того, при u[k] = u(t
k
), где t
k
= kT
0
, T
0
= const – шаг
дискретизации (период квантования), выполнено у[k] = у(t
k
) – решения
уравнений (2.81) и (2.82) совпадают при t
k
= kT
0
.
Формулы перехода к разностным уравнениям
. Рассмотрим задачу
определения матриц
DCQP ,,, в (2.82) по известным матрицам А, B, C, D
в (2.81), исходя из сформулированного выше требования эквивалентно-
сти систем по отношению к входному воздействию u(t). Для простоты
изложения ограничимся рассмотрением кусочно-постоянного процесса
вида
,,...2,1,0,,при)()(
01
=
=
<≤=
+
kkTtttttutu
kkkk
достаточно распространенного на практике, который формируется так
называемым фиксаторам или экстраполяторам нулевого порядка. Из-
вестно, что решение этой задачи с использованием аппарата передаточ-
ных функций и z-преобразования (дискретного преобразования Лапласа)
позволяет передаточную функцию дискретной модели W
D
(z) записать
следующим образом:
()
,
)(
1)(
1
−=
−
s
sW
ZzzW
(2.83)
где Z означает операцию z-преобразования переходной функции исход-
ной непрерывной системы.
Для решения аналогичной задачи в рамках метода пространства со-
стояний воспользуемся формулой Коши (2.80) и проинтегрируем первое
уравнение из (2.81) на интервале [t
k
,
t
k+1
], полагая на нем u(t)= u(t
k
). При х
0
= х(t
k
) получим
() ()
()
).()(
)()()(
1
10
1
11
1
k
t
t
tA
k
AT
t
t
tA
k
ttA
k
tBudetxe
dBuetxetx
k
k
k
k
k
kkk
+=
=+=
∫
∫
+
+
+
++
−
−−
+
υ
υυ
υ
υ
(2.84)
Если ввести новую переменную
θ
= t
k+1
–
υ
, то, вычисляя интеграл в
круглых скобках из соотношения (2.84), при t
k+1
– t
k
= Т
0
получим
,
()
∫∫
−==
−
−
+
+
0
0
1
1
0
1
)(
T
AT
A
t
t
tA
EeAdede
k
k
k
θυ
θ
υ
45

предполагая, что матрица А невырожденная.
Следовательно, выражение (2.84) можно переписать в виде
,0det),()()()(
00
1
1
≠−+=
−
+
AtBuEeAtxetx
k
AT
k
AT
k
(2.85)
а уравнение выхода, согласно второму уравнению из (2.81), представить в
виде
).()()(
kkk
tDutCxty
+
= (2.86)
Сопоставляя первое уравнение из (2.82) с уравнением (2.85) и вто-
рое уравнение из (2.82) с уравнением (2.86), получим очевидные соотно-
шения
.,,)(,
1
0
DDCCBEPAQeP
AT
==−==
−
(2.87)
Когда выполнен переход от (2.81) к (2.82), то с учетом соотношений
(2.87) можно записать уравнения
,...,1,0],[][][
,0det],[)(][]1[
00
1
=+=
≠−+=+
−
kkDukCxky
AkBuEeAkxekx
ATAT
(2.88)
которые с помощью z-преобразования и преобразований, аналогичных
соотношениям (2.67), (2.68), могут быть представлены следующим обра-
зом:
()()
()
()
.0det),(
)(
)()()(
1
1
1
00
≠+−=
=
+−−=
==
−
−
−
AzuDQPzEC
zuDBEeAezEC
zuzWzy
ATAT
(2.89)
Заметим, что передаточные функции в выражениях (2.83) и (2.89)
идентичны, но получены различными способами.
2.3.3. Вычисление матричной экспоненты
Методы вычисления матричной экспоненты e
At
обычно подразделя-
ют на точные и приближенные. Точные позволяют получить выражение
для матричной экспоненты через скалярные аналитические функции, а
приближенные – аппроксимировать ее с некоторой алгоритмической
ошибкой, зависящей от способа аппроксимации и параметров алгоритма.
46
Точные методы
. Рассмотрим аналитические выражения для матрич-
ной функции e
At
в следующих частных случаях:
1. Матрица А диагональная с вещественными собственными значе-
ниями.
Пусть А = diag{s
1
, s
2
, …, s
n
}, Im s
i
= 0, i = 1, …, n. Непосредствен-
ным вычислением суммы ряда (2.77) получаем
{
}
ts
tsts
At
n
eeee ...diag
21
= ,
где e – скалярные экспоненты.
ts
i
2. Матрица А блочно-диагональная с мнимыми собственными зна-
чениями.
Пусть А имеет собственные числа: s
1,2
=
α
± j
β
, j
2
= –1, тогда ее
можно представить в виде
−
+=
−
=
0
0
β
β
α
αβ
β
α
EA ,
а матричную экспоненту описать выражением
.
0
0
t
EtAt
eee
−
=
β
β
α
Применяя формулу (2.77), можно показать, что это соотношение
имеет вид
.
cossin
sincos
−
=
tt
tt
ee
tAt
ββ
β
β
α
3. Матрица А имеет кратные вещественные собственные значения.
Пусть s
i
= 0, i = 1,2,3, т.е. матрица А нильпотентная
,
000
100
010
=A
вычисляя степени которой получаем, что
.0...,
000
000
100
432
===
= AAA
Следовательно, ряд (2.77) точно выражается первыми тремя слагае-
мыми в виде
47

.
100
10
5.01
2
= t
tt
e
At
В случае отличных от нуля кратных вещественных собственных зна-
чений s
i
=
α
, i = 1,2,3 аналогично предыдущему получаем
.
100
10
5.01
2
= t
tt
ee
tAt
α
Если матрица А имеет произвольный вид, то всегда существует не-
вырожденное преобразование с матрицей Т такое, что подобная ей мат-
рица
A
= ТАТ
-1
– жорданова. Тогда по свойству 8 переходной матрицы
(см. 2.3.1) получаем
T
e
T
e
tAAt 1−
= .
Аналитические формулы для матричной экспоненты могут быть по-
лучены также на основе преобразования Лапласа. Этот способ основан на
том, что резольвента R(s) постоянной матрицы А является изображением
по Лапласу ее матричной экспоненты, т.е.
(
)
()
,
1−
−= AsEeL
At
причем элементы переходной матрицы можно найти с помощью таблиц
обратного преобразования Лапласа.
Приближенные методы
. Эти методы основаны на различных ап-
проксимациях ряда (2.77) выражениями, содержащими конечное число
слагаемых.
Достаточно очевидной является аппроксимация Тейлора порядка k,
согласно которой ряд (2.77) приближенно заменяется следующей конеч-
ной суммой:
.
!
)(
!
)(
...
2
)(
1
2
∑
=
+≡++++≈
k
i
ik
A
i
A
E
k
AA
AEe
θθθ
θ
θ
(2.90)
В частности, при k = 1 получаем линейное приближение вида
,
θ
θ
AEe
A
+≈ (2.91)
которое будем называть аппроксимацией Эйлера.
Аппроксимация (2.90) не является лучшей и во многих отношениях
48

уступает более общей аппроксимации Паде. При такой аппроксимации
экспонента е
х
представляется рациональной функцией
,
)(
)(
xG
xF
e
x
µν
µν
≈ (2.92)
()
(
)
()( )
()
()( )()
,
!11
121
...
!21
1
!1
1)(
2
µ
µν
µννµνµ
µµ
νµνµ
µ
µ
νµ
µ
x
xxxF
+⋅⋅⋅−++
⋅⋅⋅⋅−
+
+
−++
−
+
+
+=
(2.93)
()
(
)
()( )
()
()( )()
.
!11
121
)1(
...
!21
1
!1
1)(
2
νν
µν
νννµνµ
νν
νµνµ
ν
ν
νµ
ν
x
xxxG
+⋅⋅⋅−++
⋅⋅⋅⋅−
−+
+
−++
−
+
+
−=
(2.94)
Соответственно, для матричного аргумента x = A
θ
запишем
),()(
1
θθ
µνµν
θ
AGAFe
A −
≈ (2.95)
где F
µν
(A
θ
), G
µν
(A
θ
) – матричные многочлены вида (2.93), (2.94). В даль-
нейшем (2.95) будем называть аппроксимацией Паде (
µ
,
ν
).
Приведем некоторые частные случаи (2.95).
Во-первых, аппроксимация Тейлора (2.90) – это частный случай
(2.95) при
ν
= 0. Следовательно, выражение (2.91) совпадает с аппрокси-
мацией Паде (1, 0).
Аппроксимация Паде (0, 1) имеет вид
(
1
−
−≈
θ
θ
AEe
A
)
)
(2.96)
и далее будет называться неявным методом Эйлера.
Аппроксимация Паде (1,
1) соответствует методу Тастина и опреде-
ляется формулой
()(
.0.5 0.5
1−
−+≈
θθ
θ
AEAEe
A
(2.97)
Формула Паде (2, 2) приводит к выражению
()
(
)
.)(6 12)(6 12
1
22
−
+−++≈
θθθθ
θ
AAEAAEe
A
(2.98)
Основным преимуществом аппроксимаций Паде является их более
высокая точность, а недостатком – необходимость обращения матрицы
49

G
µν
(A
θ
) и связанная с этим проблема ее вырожденности.
2.3.4. Вычисление матрицы Q
Как уже отмечалось, формула (2.87) для вычисления матрицы Q
применима, если det A ≠ 0.
Трудностей, связанных с вычислением Q при вырожденной матрице
А, можно избежать, если при формальной подстановке выражения
0
AT
e
P
= , полученного из аппроксимаций Тейлора (2.90) или Паде (2.95),
в соотношении (2.87) выполнить "сокращение" матрицы А. Тогда в выра-
жение для Q матрица А
-1
входить не будет. В частности, аппроксимация
по методу Эйлера (2.87), (2.91) Р = Е + АТ
0
приводит к формуле Q = ВТ
0
, а
аппроксимация Паде (1, 1) (2.87), (2.97) – к формуле Q = (Е – 0.5АТ
0
)
-1
ВТ
0
.
Иной способ заключается в расширении пространства состояний ис-
ходной системы (2.81). Входной процесс и(t) при t
k
≤ t < t
k+1
рассматрива-
ется как решение некоторого однородного дифференциального уравне-
ния. Тогда расширенная система тоже однородная и в вычислении по
(2.87) нет необходимости. Искомые матрицы Р и Q получаются как под-
матрицы расширенной "матричной" экспоненты. Покажем это на приме-
ре ступенчатого входного процесса и(t) = и(t
k
) при t
k
≤ t < t
k+1
. Для ука-
занного промежутка времени уравнение состояния (2.81) запишем в виде
].[)(,0
)(
,],[)(),()(
)(
1
kutu
d
t
tdu
tttkxtxtButAx
dt
tdx
k
kkk
==
<≤=+=
+
(2.99)
Введем в рассмотрение расширенный (n + m)-мерный вектор со-
стояния
)}(,)({col)( tutxtx = и (n + m)х(n + m) матрицу
.
00
xx
=
mmmn
BA
A
Уравнение (2.99) запишем в виде
.]},[],[{col)(),(
)(
1+
<≤==
kkk
tttkukxtxtxA
d
t
txd
(2.100)
Соответствующая дискретная модель, аналог (2.82), принимает вид
.],[]1[
0
TA
ePkxPkx ==+ (2.101)
50
