Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope
Подождите немного. Документ загружается.

178 3 Physics of Electron Scattering
P
rel
= 0.04; by calculating a many-body Hamiltonian, Srivastava et al. (1982)
obtained P
rel
= 0.024.
Experimental determinations for aluminum have produced disparate values:
0.135 (Spence and Spargo, 1971), 0.07 (Batson and Silcox, 1983), <0.03 (Egerton
and Wang, 1990), and ≤0.005 (Schattschneider and Pongratz, 1988). The reason
for these discrepancies is unknown, although Schattschneider has pointed out that
small holes in the specimen or a variation in thickness would cause an overestimate
of P
rel
after Fourier log deconvolution. Although the double-plasmon process is of
interest in terms of nonlinear physics and plasmon–electron coupling, its apparent
low probability suggests that it can usually be neglected in quantitative analysis of
the low-loss spectrum.
3.5 The Spectral Background to Inner-Shell Edges
Each ionization edge in the energy-loss spectrum is superimposed on a downward-
sloping background that arises from the excitation of electrons of lower binding
energy, and which may have to be subtracted in the process of elemental analysis or
interpretation of core-loss fine structure. Since the background is often comparable
to or larger than the core-loss intensity, accurate subtraction is essential, as dis-
cussed in Chapter 4. In general, it is desirable to minimize the background intensity,
requiring an understanding of the energy-loss mechanisms that give rise to the back-
ground. In this section, we discuss contributions to the background in the case of a
very thin specimen, then consider the effect of plural scattering, which i s important
for thicker specimens.
3.5.1 Valence-Electron Scattering
For energy losses below 50 eV, inelastic scattering from outer-shell electrons is
largely a collective process in the majority of solids. A “plasmon” peak usually
occurs in the range of 10–30 eV, above which the intensity falls monotonically with
increasing energy loss. Integration of Eq. (3.32) up to a collection semi-angle β
large compared to the characteristic angle θ
E
gives
dσ/dE ∝ Im(−1/ε)ln(β/θ
E
) (3.115)
The Drude expression for Im(−1/ε), Eq. (3.43), is proportional to E
−3
for large E,
so the falloff of intensity within the plasmon “tail” should vary roughly as E
−3
,if
we ignore the logarithm term in Eq. (3.115).
At large energy loss, however, the scattering is likely to have a single-electron
character (see Section 3.3.2) and is more appropriately described by Bethe the-
ory, using the equations that will be applied to inner-shell excitation in Section
3.6. In particular, dσ /dE is expected to have a power-law energy dependence, as
in Eq. (3.154), with an exponent of the order of 4 or 5 for small values of β. Such
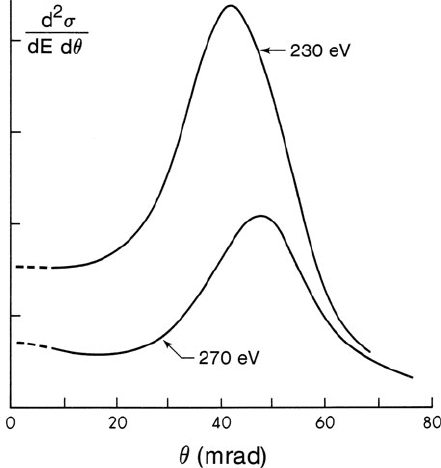
3.5 The Spectral Background to Inner-Shell Edges 179
Fig. 3.31 Angular
dependence of the
valence-electron scattering
per unit angle, recorded from
a thin carbon specimen using
80-keV electrons. Both
curves correspond to energy
losses below the K-ionization
edge (E
K
= 284 eV)
behavior was confirmed by measurements of the valence-electron scattering from
thin films of carbon, in the energy range of 100–280 eV (Egerton, 1975; Maher
et al., 1979).
Since the binding energy of a valence electron is small compared to the energy
losses under consideration, a large proportion of the background intensity will occur
at large scattering angles, in the form of a Bethe ridge (Fig. 3.36). Again, experimen-
tal data on carbon support this; see Fig. 3.31. In contrast, the inner-shell electrons
have large binding energies and their inelastic scattering is forward peaked with
an approximately Lorentzian angular distribution. Therefore, for the same energy
loss, the core-loss intensity is concentrated into smaller scattering angles than the
background. Using a small collection aperture to record the energy-loss spectrum
therefore enhances the edge/background ratio, as seen in Fig. 3.32a. However,
this small aperture results in a weak core-loss signal, giving rise to a relatively
large shot-noise component in the spectral data and a low signal/noise ratio (SNR).
Consequently, the SNR is often optimum at some intermediate value of collection
semi-angle, typically around 10 mrad; see Fig. 3.32b.
3.5.2 Tails of Core-Loss Edges
In addition to the valence electrons, inner-shell electrons of lower binding energy
may contribute intensity to the background underlying an ionization edge. If the
preceding edge is prominent and not much lower in binding energy, the angular
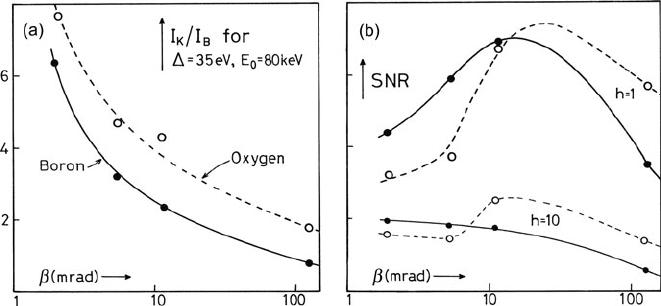
180 3 Physics of Electron Scattering
Fig. 3.32 (a) Signal/background ratio (I
K
/I
b
)and(b) signal/noise ratio (SNR) as a function of
collection semi-angle, measured for the boron and oxygen K-edges of B
2
O
3
(Egerton et al., 1976).
The parameter h is a factor that occurs in the formula for SNR (see Section 4.4.4) and depends on
the widths of the background-fitting and extrapolation regions
distribution of the background will be forward peaked and of comparable width to
that of the edge being analyzed. The advantage of a small collection angle (in terms
of signal/background ratio) is then less than where the background arises mainly
from valence-electron excitation. But if the two edges are well separated in energy,
the angular distributions may be sufficiently dissimilar to allow a significant increase
in signal/background ratio with decreasing collection angle, as in the case of the
oxygen K-edge in B
2
O
3
(Fig. 3.32a).
3.5.3 Bremsstrahlung Energy Losses
When a transmitted electron undergoes centripetal acceleration in the nuclear field
of an atom, it loses energy in the form of electromagnetic radiation (Bremsstrahlen).
Although “coherent bremsstrahlung” peaks can be recorded from crystalline speci-
mens in certain circumstances (Spence et al., 1983; Reese et al., 1984), the energy
spectrum of the emitted photons usually forms a continuous background to the
characteristic peaks observed in an x-ray emission spectrum.
The differential cross section for bremsstrahlung scattering into angles less than
β can be written as (Rossouw and Whelan, 1979)
dσ/dE = CE
−1
Z
2
(v/c)
−2
ln[1 +(β/θ
E
)
2
] (3.116)
where C = 1.55 × 10
−31
m
2
per atom. Equation (3.116) neglects screening of the
nuclear field by the atomic electrons, but is sufficient to show that (for energy losses
below 4 keV) the bremsstrahlung background in the energy-loss spectrum is small
3.5 The Spectral Background to Inner-Shell Edges 181
in comparison with that arising from electronic excitation (Isaacson and Johnson,
1975; Rossouw and Whelan, 1979).
3.5.4 Plural-Scattering Contributions to the Background
Within the low-loss region (E < 100 eV), plural scattering contributes significant
intensity unless the specimen thickness is much less than the plasmon mean free
path (of the order of 100 nm for 100-keV electrons; see Section 3.3.1). At an energy
loss of several hundred electron volts, however, multiple scattering that involves
only plasmon events makes a negligible contribution, since the required number n
of scattering events is large and the probability P
n
becomes vanishingly small as a
result of the n! denominator in Eq. (3.94). For example, a multiple plasmon loss of
10E
p
requires (on the average) 10 successive scattering events, giving P
n
< 10
−6
for a sample thickness equal to the plasmon mean free path.
Similarly, it can be shown that the probability of two or more inelastic events of
comparable energy loss is negligible when the total loss is greater than 100 eV. For
example, if the single-scattering probability P(E)isoftheformAE
−r
, the proba-
bility of two similar events (each of energy loss E/2) is 2
2r
[P(E)]
2
, which at high
energy loss is small compared to P(E) because of the rapid falloff in the differential
cross section.
However, the probability of two dissimilar energy losses can be appreciable,
as illustrated by the following simplified model (Stephens, 1980). The low-loss
spectrum is represented by a series of sharp (δ-function) peaks at multiples of
the plasmon energy E
p
, the area under each being given by Poisson statistics. The
energy dependence of the single-scattering background (arising from inner-shell or
valence single-electron excitation) is taken to be J
1
(E) = AE
−r
, with A and r as
constants. Provided that scattering events are independent, the joint probability of
several events is the product of the individual probabilities. Therefore the intensity
at an energy loss E, due to one single-electron and n plasmon events, is
J
1+n
(E) = A(E −nE
p
)
−r
(t/λ)
n
exp(−t/λ)/n! (3.117)
where λ is the plasmon mean free path. This equation allows the contributions
from different orders of scattering to be compared for different values of t/λ;
see Fig. 3.33 and Appendix B, Section B.10.
Plural scattering contributions to an ionization edge can be evaluated in a similar
way (Fig. 3.33). Since the double (core-loss + plasmon) scattering is delayed until
an energy loss E = E
k
+ E
p
, the core-loss intensity just above the threshold E
k
represents only single core-loss scattering. Defining the jump ratio (JR) of the edge
as the height of the initial rise divided by the intensity of the immediately preceding
background, JR is seen to decrease with increasing specimen thickness, because of
plural scattering contributions to the background; see Fig. 3.33.
An alternative measure of edge visibility is the signal/background ratio (SBR),
measured as core-loss intensity integrated over an energy range above the
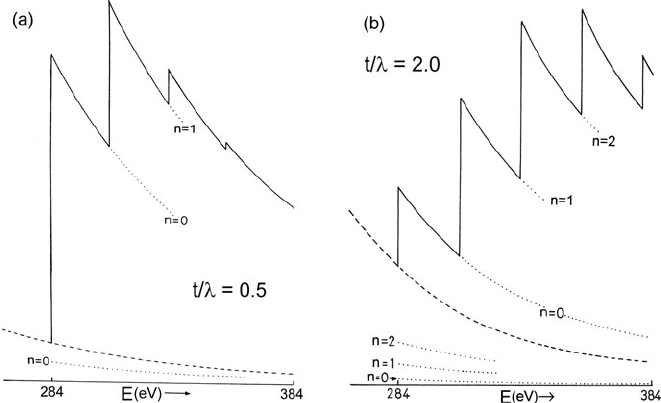
182 3 Physics of Electron Scattering
Fig. 3.33 Contribution of plasmon scattering (up to order n) to the carbon K-edge (solid lines)and
to its background (dashed curve), calculated using Eq. ( 3.117). In this simple model, the contribu-
tion of each successive order to the edge profile is visible as a sharp step in intensity; in practice,
these steps are rounded and in some materials barely visible. The specimen thickness is (a) one
half and (b) twice the total-inelastic mean free path
threshold, divided by the background integrated over the same energy range. SBR
decreases with thickness less rapidly than JR because some plural scattering is
included in the core-loss integral and for sufficiently large , SBR should vary
little with specimen thickness. In practice, plural scattering makes background
extrapolation and measurement of the core-loss integral more difficult in thicker
specimens.
Despite the approximations involved, Eq. (3.117) agrees quite well with mea-
surements of SBR for low-energy ionization edges; see Fig. 3.34a. In the case of
higher energy edges (Fig. 3.34b), the agreement can be less satisfactory because of
spectrometer contributions to the background (Section 2.4.1). Although extremely
thin specimens give the highest signal/background ratio, the core-loss signal itself is
very weak, resulting in a high fractional noise content. As a result, the signal/noise
ratio (SNR) is optimum at some intermediate thickness, as illustrated in Fig. 3.34b.
SNR determines the visibility of an edge and the minimum detectable concentration
in elemental analysis; see Section 5.5.4.
A more general method of computing plural scattering contributions is by
self-convolution of the single-scattering energy distribution. Using this approach,
Leapman and Swyt (1983) showed that plural scattering can cause the background
exponent r to decrease with increasing sample thickness; see Fig. 3.35. The change
in r is particularly large for energy losses just above a major ionization edge (e.g., in
the range of 300–400 eV for a carbonaceous sample) and is attributable to a change
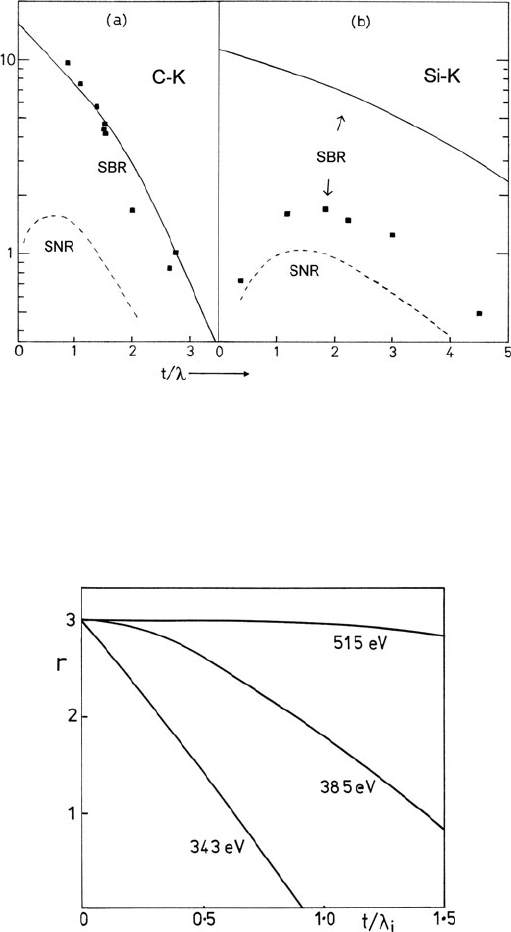
3.5 The Spectral Background to Inner-Shell Edges 183
Fig. 3.34 Signal/background ratio (SBR) and signal/noise ratio (SNR) for K-edges of (a)elemen-
tal carbon and (b) pure silicon, as a function of specimen thickness. Solid curves represent Eq.
(3.117)andsquares are measurements for 10-mrad collection semi-angle, 1-keV incident energy,
and 100-eV integration windows. SNR (in arbitrary units) was calculated as I
k
/(I
k
+hI
b
)
1/2
,as
discussed in Section 4.4.3
Fig. 3.35 Change in the slope parameter r that characterizes the energy dependence (AE
–r
)ofa
carbon loss spectrum, calculated as a function of specimen thickness t (Leapman and Swyt, 1983).
The four chosen values of energy loss would immediately precede minor edges due to calcium,
nitrogen, and oxygen in the spectrum of a biological specimen. The s lope parameter is assumed
to be constant and equal to 3 in the absence of plural scattering (t = 0). From Leapman and Swyt
(1983), with permission from San Francisco Press
184 3 Physics of Electron Scattering
in overall shape of the major edge as a result of “mixed” scattering (see Section
3.7.3). The pre-edge background and jump ratio can also be calculated by Monte
Carlo methods (Jouffrey et al., 1985), allowing the precise effects of a collection
aperture to be included.
3.6 Atomic Theory of Inner-Shell Excitation
Inner-shell electrons have relatively large binding energies and the associated energy
losses are typically some hundreds of electron volts, corresponding to the x-ray
region of the electromagnetic spectrum. As a result of this strong binding to the
nucleus, collective effects are relatively unimportant. Inner-shell excitation can
therefore be described to a first approximation in terms of single-atom models.
3.6.1 Generalized Oscillator Strength
The key quantity in Bethe theory (Section 3.2.2) is the generalized oscillator
strength (GOS) that describes the response of an atom when a given energy and
momentum are supplied from an external source (e.g., through collision of a fast
electron). In order to calculate the GOS, it is necessary to know the initial- and final-
state wavefunctions of the inner-shell electron. Calculations are based on several
different methods.
3.6.1.1 The Hydrogenic Model
The simplest way of estimating the GOS, and the first to be developed (Bethe,
1930), is based on wave mechanics of the hydrogen atom. This approach is of
interest in energy-loss spectroscopy because it provides realistic values of K-shell
ionization cross sections with a minimum amount of computing, enabling cross
sections needed for quantitative elemental analysis to be calculated online. This
relative simplicity arises from the fact that analytical expressions are available
for the wavefunctions of the hydrogen atom, obtained by solving the Schrödinger
equation:
(−
2
/2m
0
)∇
2
ψ −(e
2
/4πε
0
r)ψ = E
t
ψ (3.118)
where E
t
is the “net” (kinetic + electrostatic) energy of the atomic electron.
To make Eq. (3.118) applicable to an inner-shell electron within an atom of
atomic number Z, the electrostatic term must be modified to take into account
the actual nuclear charge Ze and screening of the nuclear field by the remaining
(Z − 1) electrons. Following Slater (1930), an effective nuclear charge Z
s
e is used
in the Schrödinger equation. In the case of K-shell excitation, the second 1s elec-
tron screens the nucleus and reduces its effective charge by approximately 0.3e,
giving Z
s
= Z − 0.3. For L-shell excitation: Z
s
= Z − (2 × 0.85) − (7 × 0.35),

3.6 Atomic Theory of Inner-Shell Excitation 185
allowing for the screening effect of the two K-shells and seven remaining L-shell
electrons. Outer electrons (all those whose principal quantum number is higher than
that of the initial-state wavefunction) are assumed to form a spherical shell of charge
whose effect is to reduce the inner-shell binding energy by an amount E
s
, so that the
observed threshold energy for inner-shell ionization is
E
k
= Z
2
s
R −E
s
(3.119)
where R = 13.6 eV is the Rydberg energy. The Schrödinger equation of the atom is
therefore
(−
2
/2m
0
)∇
2
ψ −(Z
s
e
2
/4πε
0
r)ψ +E
s
ψ = E
t
ψ (3.120)
The net energy E
t
of the excited electron is related to its binding energy E
k
and the
energy E lost by the transmitted electron:
E
t
= E −E
k
(3.121)
Substituting Eqs. (3.119) and (3.120) into Eq. (3.121)gives
(−
2
/2m
0
)∇
2
ψ −(Z
s
e
2
/4πε
0
r)ψ = ( E −Z
2
s
R)ψ (3.122)
This is the Schrödinger equation for a “hydrogenic equivalent” atom with nuclear
charge Z
s
e and no outer shells. Since the wavefunctions remain hydrogenic (or
“Coulombic”) in form, standard methods can be used to solve for the wavefunction
ψ and for the GOS.
For convenience of notation, we can define dimensionless variables Q’ and k
H
that are related (respectively) to the scattering vector q and the energy loss E of the
fast electron:
Q
= (qa
0
/Z
s
)
2
(3.123)
k
2
H
= E/(Z
2
s
R) −1 (3.124)
The generalized oscillator strength (GOS) per atom is then given, for E > Z
2
s
R and
for K-shell ionization (Bethe, 1930; Madison and Merzbacher, 1975), by
df
K
dE
=
256E(Q
+k
2
H
/3 +1/3) exp(−2β
/k
H
)
Z
4
s
R
2
[(Q
−k
2
H
+1)
2
+4k
2
H
]
3
[1 −exp(−2π/k
H
)]
(3.125)
where β
is the value of arctan [2k
H
/(Q
−k
2
H
+1)] that lies within the range 0 to π.
Energy losses in the range E
k
< E < Z
2
s
R correspond to transitions to discrete states
in the hydrogenic equivalent atom and an imaginary value of k
H
. Substitution of this
imaginary value in Eq. (3.125) gives (Egerton, 1979)

186 3 Physics of Electron Scattering
df
K
dE
=
256E(Q
+k
2
H
/3 +1/3) exp(y)
Z
4
s
R
2
[(Q
−k
2
H
+1)
2
+4k
2
H
]
3
(3.126)
where
y =−(−k
2
H
)
−1/2
log
e
Q
+1 −k
2
H
+2(−k
2
H
)
1/2
Q
+1 −k
2
H
−2(−k
2
H
)
1/2
(3.127)
Corresponding hydrogenic formulas have been derived for the L-shell GOS (Walske,
1956; Choi et al., 1973) and for M-shell ionization (Choi, 1973).
3.6.1.2 Hartree–Slater Method
Accurate wavefunctions have been computed for most atoms by iterative solution
of the Schrödinger equation with a self-consistent atomic potential. The Hartree–
Slater (HS or HFS) method represents a simplification of the Hartree–Fock (HF)
procedure, by assuming a central (spherically symmetric) field within the atom. The
resulting wavefunctions are close to those obtained using the HF method but require
much less computing. The radial component φ
0
(r) of the ground-state wavefunction
has been tabulated by Herman and Skillman (1963). For calculation of the GOS, the
final-state radial function φ
n
is obtained by solving the radial Schrödinger equation
for a net (continuum) energy E
t
:
2
2m
0
d
2
dr
2
−V(r) −
l
(l
+1)
2
2m
0
r
2
+E
t
φ
n
(r) = 0 (3.128)
where l’ is the angular momentum quantum number of the final (continuum) state.
Using a central-field model, it is not possible to provide an exact treatment of
electron exchange, but an approximate correction can be made by assuming an
exchange potential of the form (Slater, 1951)
V
x
=−6[(3/8π )ρ(r)]
−1/3
(3.129)
where ρ(r) is the spherically averaged charge density within the atom.
The transition matrix element, defined by Eq. (3.23), can be written (Manson,
1972)as
|ε
nl
|
2
=
l
(2 l
+1)
λ
(2λ +1)
⎡
⎣
∞
0
φ
0
(r)J
λ
(qr)φ
n
(r)dr
⎤
⎦
2
l
λ l
000
2
(3.130)
where the operator exp(iq ·r) has been expanded in terms of spherical Bessel f unc-
tions J
λ
(qr) and the integration over angular coordinates is represented by a Wigner
(3 − j) matrix. The GOS is obtained from Eq. (3.24), summing over all important
3.6 Atomic Theory of Inner-Shell Excitation 187
partial waves corresponding to different values of l
. Such calculations have been
carried out by McGuire (1971), Manson (1972), Scofield (1978), Leapman et al.
(1980), and Rez (1982, 1989); the results will be discussed later in this section and
in Section 3.7.1.
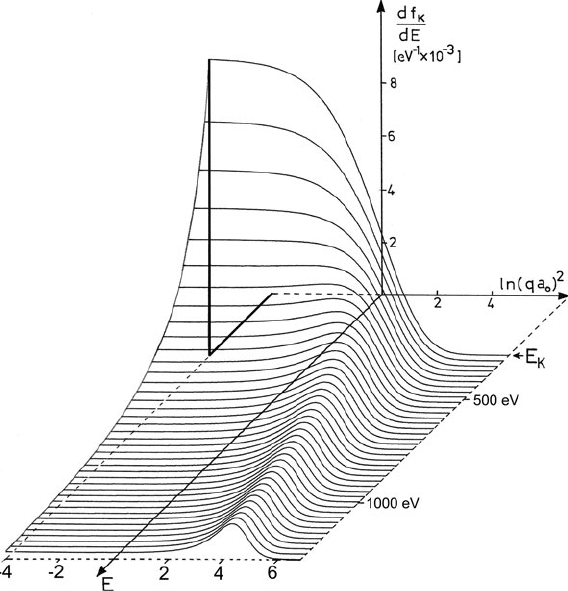
3.6.1.3 E- and q-Dependence of the GOS
The generalized oscillator strength is a function of both the energy E and the
momentum q supplied to the atom and is conveniently portrayed as a two-
dimensional plot known as a Bethe surface, an example of which is shown in
Fig. 3.36. The individual curves in this figure represent qualitatively the angu-
lar dependence of inner-shell scattering, since the double-differential cross section
d
2
σ /ddE is proportional to E
−1
q
−2
df /dE,asinEq.(3.26), while q
2
increases
approximately with the square of the scattering angle, as in Eq. (3.27). For an energy
loss not much larger than the inner-shell binding energy E
k
, the angular distribution
Fig. 3.36 Bethe surface for K-shell ionization of carbon, calculated using a hydrogenic model.
The generalized oscillator strength is zero for energy loss E below the ionization threshold E
K
.
The horizontal coordinate is related to scattering angle. From Egerton (1979), copyright Elsevier
