Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

158 3 Physics of Electron Scattering

For

 θ

, the intensity falls proportional to θ

−3

rather than θ

−2

,asinthe

case of bulk losses. This means that a small collection aperture, displaced off-axis

by a few θ

, can largely exclude surface contributions to the loss spectrum (Liu,

1988).

For nonnormal incidence, f (θ, θ

, ψ) = f (− θ , θ

, ψ), leading to an asym-

metrical angular distribution that has a higher maximum intensity as a result of the

cos

denominator in Eq. (3.76). This asymmetry has been veriﬁed experimentally

(Kunz, 1964; Schmüser, 1964). The zero in dP

/d again corresponds to the case

where the momentum transfer  q occurs in a direction perpendicular to the surface.

The total probability for surface plasmon excitation at a single vacuum interface

is obtained by integrating Eq. (3.75) over all θ. For normal incidence (θ

= 0) the

result is (Stern and Ferrell, 1960)

π

v(1 +ε

)

4ε

v(1 +ε

)

(3.77)

At 100-keV incident energy, P

is 0.021 for ε

= 1 (vacuum/metal interface) and

0.011 for ε

= 3 (typical of many oxides). Taking into account both surfaces,

the probability of surface plasmon excitation in an oxidized aluminum sample is

therefore about 2% and the corresponding loss peak (at just over 7 eV) is clearly

visible only in rather thin samples, where the inelastic scattering due to bulk pro-

cesses is weak. However, if the specimen is tilted away from normal incidence, P

is increased as a result of the cos θ

term in Eq. (3.76).

3.3.5.2 Dielectric Formulation for Surface Losses

The free-electron approximation ε

= 1 − ω

/ω

can be avoided by characterizing

the materials (conductors or insulators) on both sides of the boundary by frequency-

dependent permittivities ε

and ε

. Dielectric theory then provides an expression

for the differential “probability” of surface scattering at a single interface (Raether,

1980):

d dE

cos θ



(ε

−ε

)

(ε

+ε

)



cos θ



−4

+ε



(3.78)

assuming that the electron remains in the plane of incidence (ψ = 0). The last two

terms in Eq. (3.78) represent the begrenzungs effect, a reduction in the bulk plasmon

intensity (see later). In the small-angle approximation, q

= k

(θ

+ θ

) and (see

Fig. 3.22)

= k

θ cos θ

sin θ

(3.79)

where q

is the wavevector of the surface plasmon, equal to the component of the

scattering vector that lies parallel to the surface. One of the terms in Eq. (3.79)

3.3 Excitation of Outer-Shell Electrons 159

is negative if θ and θ

are of opposite sign. Note that Eqs. (3.78) and (3.71)are

symmetric in ε

and ε

, so the direction of travel of the incident electron is unim-

portant. The width of the plasmon peak is determined by the imaginary parts of the

permittivities on both sides of the boundary.

For the case of perpendicular incidence ( θ

= 0), Eq. (3.78) can be integrated up

to a scattering angle β to give

≈

2πa



tan

−1

(β/θ

)

−

(β

+θ

)





−4

+ε



(3.80)

for a single interface, where T = m

/2.

3.3.5.3 Very Thin Specimens

The surface plasmons excited on each surface of a specimen of thickness t are almost

independent of each other if

t ≈ k

θt  1 (3.81)

For 100-keV i ncident electrons (k

= 1700 nm

−1

), θ

= 0 and θ ≈ θ

√

3 ≈

0.1 mrad (the most probable angle of surface scattering; see Fig. 3.22), Eq. (3.81)

implies t  10 nm. If this condition is not fulﬁlled, the electrostatic ﬁelds originat-

ing from the two surfaces overlap and the surface plasmons interact with each other;

see Fig. 3.23. In the case of a free-electron metal bounded by similar dielectrics

(ε

= ε

= ε and ε

= 1 − ω

/ω

) the resonance is split into two modes, the fre-

quency of each being q-dependent and given approximately, for large q

, by (Ritchie,

1957)

= ω



1 ±exp(−q

1 +ε



1/2

(3.82)

The symmetric mode, where like charges face one another (Fig. 3.23b), corresponds

to the higher angular frequency. For small q

,Eq.(3.82) does not apply; relativistic

constraints (Kröger, 1968) cause ω to lie below

the photon line (ω = cq

)on

the dispersion diagram, as shown in Fig. 3.24. This dispersion behavior has been

veriﬁed experimentally (Pettit et al., 1975).

Assuming normal incidence and neglecting retardation effects, the differential

probability for surface excitation at both surfaces of a ﬁlm of permittivity ε

and

thickness t can be expressed (Raether, 1967)as

There are, in fact, radiative surface plasmons that lie above this line, but they are less easily

observed in the energy-loss spectrum because for small scattering angles their energy is the same

as that of the volume plasmons (see Fig. 3.24).

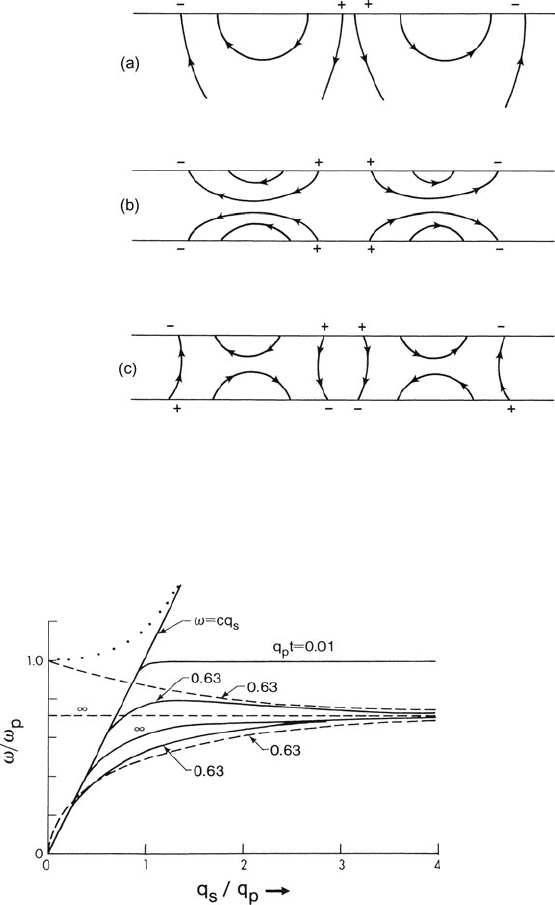
160 3 Physics of Electron Scattering

Fig. 3.23 Electric ﬁeld lines

associated with surface

plasmons excited (a)inabulk

sample and (b, c)inavery

thin ﬁlm. The plasmon

frequency is higher in the

symmetric mode (b)thanin

the asymmetric one (c)

Fig. 3.24 Dispersion diagram for surface plasmons. The dashed lines represent Eq. (3.82); the

solid curves were calculated taking into account retardation, for ﬁlm thicknesses given by q

t =

0.01, 0.63, and ∞,whereq

= ω

/c.Forθ

= 0, the horizontal axis is approximately proportional

to scattering angle θ of the fast electron, since q

≈ (v/c)

−1

(θ/θ

). The dispersion relation of

a radiative plasmon is shown schematically by the dotted curve. From Raether (1980), copyright

Springer-Verlag

3.3 Excitation of Outer-Shell Electrons 161

d dE

(θ

+θ

)



(ε

−ε

)



(3.83)

where T = m

/2 and

sin

(tE/2v)

+ε

tanh(q

t/2)

cos

(tE/2v)

+ε

coth(q

t/2)

(3.83a)

For large ﬁlm thickness, R

becomes equal to ε

/(ε

+ ε

), where ε

is the permit-

tivity of the surroundings (ε

= 1 for vacuum). A relativistic version of Eq. (3.83),

given by Kröger (1968), shows that relativistic effects modify the dispersion relation

of the surface plasmon (particularly at low q

) and result in slightly lower resonance

energies, in closer agreement with experiment.

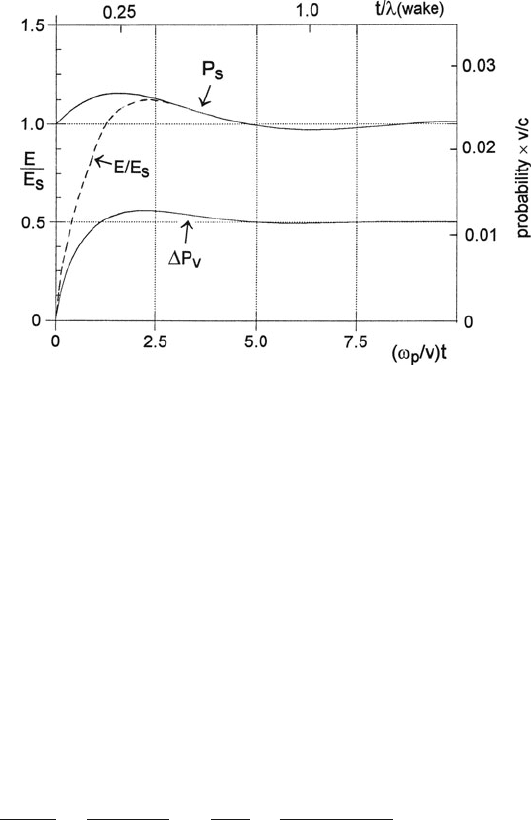
Integrating Eq. (3.83) over energy loss, Ritchie (1957) investigated how the total

probability P

of surface plasmon loss (for a free-electron metal) varies with sample

thickness. For t  ν/ω

(=7.2 nm for E

= 100 keV, E

= 15 eV), P

becomes

independent of thickness and tends asymptotically to e

/(4ε

v), twice the value

given by Eq. (3.77) since the specimen has two surfaces. For t < 5(v/ω

), the

surface-loss probability increases slightly (see Fig. 3.25), corresponding to increase

in the asymmetric (ω

−

) surface mode. But as shown by Eq. (3.82), the energy loss

associated with this mode tends to zero as t → 0, so the t otal energy loss due to

surface plasmon excitation falls toward zero for very thin ﬁlms, as indicated by the

dashed curve in Fig. 3.25.

3.3.5.4 Begrenzungs Effect

A secondary effect of surface plasmon excitation is t o reduce the intensity of the

bulk plasmon peak, the begrenzungs (boundary) effect. Within a distance of the

order of v/ω

of each surface, the transmitted electron excites surface rather than

bulk plasmons. This effect gives rise to a negative value of the energy-loss function

at E   ω

, represented by the −Im(−1/ε

) and −Im(−1/ε

)termsinEqs.(3.78)

and (3.80).

For t > v/ω

, the calculated reduction P

in the probability P

of volume

plasmon excitation is just equal to the probability of surface plasmon generation at

a single surface (see Fig. 3.25), which is typically about 1% and small compared

to P

. However, this negative surface contribution occurs mainly at small angles

(θ ≈ θ

), due to the relatively narrow angular distribution of the surface-loss inten-

sity. Its effect is therefore greater if the energy-loss spectrum is recorded with a

small angular-collection aperture. For an effective aperture of 0.2 mrad and 50-keV

electrons transmitted through a ﬁlm of aluminum, Raether (1967) reported a reduc-

tion in the volume-loss intensity of 8% at t = 100 nm, increasing to over 40% at

t = 10 nm.

162 3 Physics of Electron Scattering

Fig. 3.25 Thickness dependence of the probability P

of surface plasmon excitation and the asso-

ciated energy loss (in units of E

/2, dashed curve) for normally incident electrons of speed v,

calculated using a free-electron model for a specimen with two clean and parallel surfaces. From

Ritchie (1957), copyright American Physical Society. The lower curve shows the reduction P

in the probability of volume plasmon excitation, the begrenzungs effect. This effect has also been

calculated for the case of a small sphere (Echenique et al., 1987). Available at http://link.aps.org/

abstract/PR/v106/p874

3.3.5.5 Retardation effects

By solving Maxwell’s equations with appropriate boundary conditions, Kröger

(1968) derived an expression for the differential probability of energy loss in a spec-

imen of thickness t, including volume and surface losses, transition radiation, and

retardation effects. Using notation similar to that of Erni and Browning (2008), the

differential probability for a specimen of thickness t is

d dE



tμ

∗

−

2θ

(ε

∗

−η

∗

)

(A +B +C)



(3.84)

Here ε

∗

= ε

− i ε

is the complex conjugate of the dielectric f unction of the

specimen and η

∗

is an equivalent quantity for the surroundings (η = relative per-

mittivity of the oxide, for a loss-free oxide coating on each surface). The angular

terms φ

= λ

+ θ

and φ

= λ

+ θ

, where λ

= θ

− ε

∗

(v/c)

and

= θ

−η

∗

(v/c)

, are dimensionless, as is μ

= 1 −ε

∗

(v/c)

The ﬁrst term in square brackets represents the

Cerenkov-enhanced volume loss,

equivalent to Eq. (3.70), the other terms representing surface plasmon excitation and

the effect of the surfaces on

Cerenkov emission. The surface plasmon term is

3.3 Excitation of Outer-Shell Electrons 163

A =

∗



sin

cos

−



(3.84a)

where d

= πtE/(hv), L

= λ

∗

+ λη

∗

tanh(λd

/θ

), and L

−

= λ

∗

λη

∗

coth(λd

/θ

), as in Eq. (3.83a). The remaining terms account for guided-light

modes in the specimen:

B =

∗



−



sin(2d

) (3.84b)

C =

−v

λθ



cos

tanh(λd

/θ

)

sin

coth(λd

/θ

)

−



(3.84c)

where φ

= θ

+θ

[1 −(ε

∗

−η

∗

)(v

)].

Equation (3.84) can be used to predict the angular and thickness dependence of

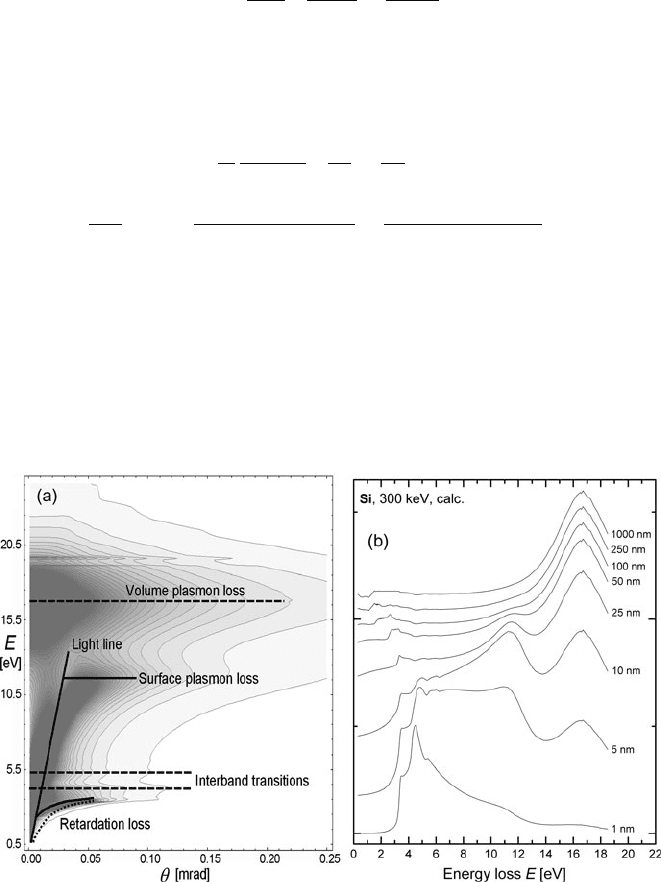
the low-loss spectrum, as illustrated in Fig. 3.26. In silicon, the retardation effects

are seen to occur at even smaller angles and energy loss than the surface plasmon

loss, and their energy dependence is sensitive to specimen thickness below about

1000 nm. For very thin specimens ( t < 5 nm), the surface and bulk plasmon peaks

largely disappear, leaving retardation and interband transitions as the main spectral

Fig. 3.26 (a) Schematic and contour plot (gray background) showing the calculated energy loss

and angular dependence of intensity for a 50-nm Si specimen and 300-keV incident electrons.

(b) Energy-loss spectra calculated from Eq. (3.84) for 2.1-mrad collection semi-angle, 300-keV

incident electrons, and various thicknesses of silicon, assuming no surface-oxide later. The inten-

sities are normalized and the spectra displaced vertically for clarity. Reproduced from Erni and

Browning (2008), copyright Elsevier. A computer program for evaluating Eq. (3.84) is described

in Appendix B9

164 3 Physics of Electron Scattering

features below 10 eV. This implies that direct bandgap measurements are most reli-

ably made on isolated ultrathin structures, such as suspended nanotubes (Yurtsever

et al., 2008).

For silicon specimens of thickness between 25 and 310 nm, the E-dependence of

scattering probability (for E < 5 eV) calculated from Eq. (3.84) shows good agree-

ment with experiment (Yurtsever et al., 2008). Equation (3.84) can be generalized to

the case of nonnormal incidence (Kröger, 1970; Mkhoyan et al., 2007). Anisotropic

materials introduce further complications (Chen and Silcox, 1979). Cerenkov exci-

tation by aloof electrons and adjacent to curved surfaces is analyzed by Garcia de

Abajo et al. (2004).

3.3.6 Surface-Reﬂection Spectra

Instead of measuring transmitted electrons, energy-loss spectra can be recorded

from electrons that have been reﬂected from the surface of a specimen. The depth of

penetration of the electrons (perpendicular to the surface) depends on the primary

beam energy and the angle of incidence θ

(see Fig. 3.27). For moderate angles,

both bulk- and surface-loss peaks occur in the reﬂection spectrum; at a glancing

angle (θ

> 80

◦

) the penetration depth is small and only surface peaks are observed,

particularly if the spectrum has been recorded from specularly reﬂected electrons

(angle of reﬂection = angle of incidence) and the incident energy is not too high

(Powell, 1968).

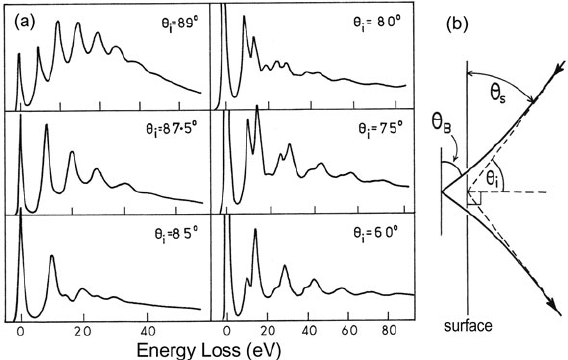
Fig. 3.27 (a) Plasmon-loss spectra recorded by reﬂection of 8-keV electrons from the unoxidized

surface of liquid aluminum. At glancing incidence, the spectrum is dominated by plural scattering

from surface plasmons; as the angle of incidence is reduced, volume plasmon peaks appear at

multiples of 15 eV. (b) Reﬂection of an electron at the surface of a crystal, showing the difference

between the angles θ

and θ

due to refraction. From Powell (1968), copyright American Physical

Society. Available at http://link.aps.org/abstract/PR/v175/p972

3.3 Excitation of Outer-Shell Electrons 165

In the case of a crystalline specimen, the r eﬂected intensity is strong when the

angle between the incident beam and the surface is equal to a Bragg angle for atomic

planes which lie parallel to the surface,thespecular Bragg condition. The intensity

is further increased by adjusting the crystal orientation so that a resonance parabola

seen in the reﬂection diffraction pattern (the equivalent of a Kikuchi line in trans-

mission diffraction) intersects a Bragg-reﬂection spot, such as the ( 440) reﬂection

for a {110} GaAs surface, giving a surface-resonance condition. The penetration

depth of the electrons is then only a few monolayers, but the electron wave travels a

short distance (typically of the order of 100 nm) parallel to the surface before being

reﬂected (Wang and Egerton, 1988).

The ratio P

of the integrated surface plasmon intensity, relative to the zero-loss

intensity in a specular Bragg-reﬂected beam, has been calculated on the basis of

both classical and quantum-mechanical theory (Lucas and Sunjic, 1971; Evans and

Mills, 1972). For a clean surface (ε

= 1) and assuming negligible penetration of

the electrons,

= e

/(8ε

v cos θ

) (3.85)

which is identical to the formula for perpendicular transmission through a single

interface, Eq. (3.77), except that the incident velocity v is replaced by its compo-

nent v(cos θ

) normal to the surface. In the case of measurements made at glancing

incidence, this normal component is small and P

may approach or exceed unity.

Surface peaks then dominate the energy-loss spectrum (see Fig. 3.27); bulk plas-

mons are observed only for lower values of θ

or (owing to the broader angular

distribution of volume scattering) when recording the spectrum at inelastic scat-

tering angles θ away from a specular beam (Schilling, 1976; Powell, 1968). An

equivalent explanation for the increase in surface loss as θ

→ 90

◦

is that the

incident electron spends a longer time in the vicinity of the surface (Raether, 1980).

Schilling and Raether (1973) have reported energy gains of  ω

in energy-loss

spectra of 10-keV electrons reﬂected from a liquid-indium surface at θ

≈ 88.5

◦

Such processes were measurable only with an incident beam current so high that the

time interval between the arrival of the electrons was comparable with the surface

plasmon relaxation time. Even under the somewhat-optimized conditions used in

this experiment, the probability of energy gain was only about 0.2%.

The electron microscope allows a reﬂection diffraction pattern to be observed

and indexed, so the value of the incident angle θ

can be obtained from the Bragg

angle θ

of each reﬂected beam, provided allowance is made for refraction of the

electron close to the surface (see Fig. 3.27b). The refraction effect depends on the

mean inner potential φ

of the specimen; using relativistic mechanics to calculate

the acceleration of the incident electron toward the surface gives

Strictly speaking, P

is a “scattering parameter” analogous to t/λ in Section 3.3.6, but approxi-

mates a single-scattering probability if much less than unity.

166 3 Physics of Electron Scattering

cos

= sin

−

2(eφ

)(1 −v

)

3/2

)

(3.86)

Since cos θ

= sin θ

 θ

, where θ

is the angle between the incident beam

and the surface (measured outside the specimen), Eq. (3.86) leads to the rela-

tion P

= constant, which has been veriﬁed experimentally (Powell, 1968;

Schilling, 1976; Krivanek et al., 1983). For a given Bragg reﬂection, the value of

calculated from Eqs. (3.85) and (3.86) tends to increase with increasing inci-

dent energy; for the symmetric (333) reﬂection from silicon, for example, P

1.06 at 20 keV and 1.36 at 80 keV. Experimental values (Krivanek et al., 1983)

are somewhat higher (1.4 and 1.8), probably because Eq. (3.85) neglects surface

plasmon excitation during the brief period when the electron penetrates inside the

crystal.

Reﬂection energy-loss spectroscopy is a more surface-sensitive technique when

the incident energy is low, partly because the electron penetration depth is smaller

(the extinction distance for elastic scattering is proportional to electron velocity

v) and because the electrostatic ﬁeld of a surface plasmon extends into the solid

to a depth of approximately 1/q

≈ (k

)

−1

= v/ω

(for θ

≈ π/2), which is

proportional to the incident velocity.

3.3.6.1 Nonpenetrating Incident Beam (Aloof Excitation)

It is possible to measure energy losses of primary electrons that pass close to a

surface but remain outside, such as when a ﬁnely focused electron beam is directed

parallel to a face of a cubic MgO crystal (Marks, 1982). In the case of a metal, bulk

plasmons are not excited and surface excitations can be studied alone. Classical,

nonrelativistic theory gives for the excitation probability (Howie, 1983)

(x, E)

πm

(2ωx/v)Im



ε(E) −1

ε(E) +1



(3.87)

where z is the length of the electron path parallel to the surface (a distance x away),

(2ωx/v) is a modiﬁed Bessel function and ε(E) is the complex permittivity of

the specimen, which is a function of the energy loss E =  ω. Equation (3.87) can

be generalized to deal with the case where the specimen surface is curved (Batson,

1982; Wheatley et al., 1984) or where the incident electron executes a parabolic

trajectory as a result of a negative potential applied to the sample (Ballu et al., 1976).

A range of impact parameter x can be selected by scanning the incident beam and

using a gating circuit to switch t he spectrometer signal on or off in response to

the output of a dark-ﬁeld detector (Wheatley et al., 1984). Bertsch et al. (1998)

used dielectric theory to derive a formula for the energy-loss spectrum of electrons

passing at different distances from a cylindrical nanowire.

3.3 Excitation of Outer-Shell Electrons 167

3.3.6.2 Cross-Sectional Specimens

Cross-sectional TEM specimens, of electronic devices for example, often contain

interfaces that are perpendicular to the plane of the specimen and therefore parallel

to the incident electron beam or can be made so by slightly tilting the speci-

men. Bolton and Chen (1995a, b, c) applied dielectric theory (including retardation

effects) to electrons traversing multilayers at both parallel and perpendicular inci-

dence, and also moving within anisotropic media. Discrepancies with experimental

results are discussed by Neyer et al. (1997) in terms of coupled interface modes and

the begrenzungs effect. Moreau et al. (1997) measured energy-loss spectra for elec-

trons traveling within 10 nm of a Si–SiO

boundary and showed that a relativistic

analysis (Garcia-Mollina et al., 1985), including retardation effects, was necessary

to account for shift of a 7-eV peak with distance of the electron trajectory from the

interface.

Theories of interface excitation have usually assumed that the interface is abrupt.

The case of diffuse interface was investigated by Howie et al. (2008), who showed

that for electrons traveling at various distances parallel to an interface, the plas-

mon peaks differ in position, width, and shape from those expected for an abrupt

interface and from the volume plasmon peaks that would reﬂect the local chemical

composition.

3.3.7 Plasmon Modes in Small Particles

In the case of small particles, the surface-plasmon traveling waves become standing

waves that can be characterized by the number of nodes, somewhat like the modes

of vibration of a mechanical system. For an isolated spherical particle (relative

permittivity ε

) surrounded by a medium of permittivity ε

, the surface-resonance

condition is modiﬁed from Eq. (3.71) to become

+[l/(1 +l)]ε

= 0 (3.88)

where l is an integer. For a free-electron metal, Eq. (3.88) gives for the surface-

resonance frequency:

= ω

[1 +ε

(l +1)/l]

−1/2

(3.89)

The lowest frequency of these localized plasmonic modes corresponds to l = 1

(dipole mode) and predominates in very small spheres (radius r <10nm).Asthe

radius increases, the energy-loss intensity shifts to higher order modes and the reso-

nance frequency increases asymptotically toward the value given by Eq. (3.73)fora

ﬂat surface. This behavior was veriﬁed by experiments on metal spheres (Fujimoto

and Komaki, 1968; Achèche et al., 1986), colloidal silver and gold particles embed-

ded in gelatin (Kreibig and Zacharias, 1970), and irradiation-induced precipitates of

sodium and potassium in alkali halides (Creuzburg, 1966).