Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

168 3 Physics of Electron Scattering

The probability of exciting a given mode, averaged over all possible trajectories

of the fast electron, is of the form (Fujimoto and Komaki, 1968)

(l)

dω

8r





ωω



(ω

−ω

)

+ω



(2 l +1)

∞



ωr/v

(z)]

dz (3.90)

where  = 1/τ is the damping constant of the metal and J

is a spherical

Bessel function. Stöckli et al. (1997) measured plasmon-loss spectra of aluminum

nanospheres and carbon nanotubes of various diameters, interpreting the results in

terms of dielectric theory; see also Garcia de Abajo and Howie ( 2002).

Dielectric theory has also been used to predict the additional peaks that occur

when spherical metal particles are attached to a substrate (Wang and Cowley,

1987; Ouyang and Isaacson, 1989; Zabala and Rivacoba, 1991). For the case of

small spheres embedded in a medium, Howie and Walsh (1991) have proposed

an effective energy-loss function Im(−1/ε)

eff

that is geometrically averaged over

different segments of a typical electron trajectory. They show that this function

predicts the observed spectrum of irradiated AlF

(containing small Al particles)

more successfully than effective medium theories, which give formulas for an effec-

tive permittivity ε

eff

. Measurement of Im(−1/ε)

eff

might yield the average size and

volume fraction of ﬁne precipitates or point-defect clusters in specimens whose

structure i s too ﬁne in scale or too complex to permit direct imaging.

Cavities in a metal or dielectric also have characteristic resonance frequencies,

given for the case of a spherical void (ε = 1) in a metal by

= ω

[(m +1)/(2m +1)]

1/2

(3.91)

The frequency decreases toward ω

√

2 as the integer m increases from zero

(Raether, 1980). As an example, helium-ﬁlled “voids” in Al/Li alloy ( ω

= 15 eV)

appear bright in the image formed from 11-eV loss electrons (Henoc and Henry,

1970).

If a spherical particle becomes oblate, its surface plasmon resonance splits into

two modes, longitudinal and transverse to the long axis, the transverse mode having

a somewhat higher energy. A similar situation exists for a dimer consisting of two

spherical particles or a chain of such particles: as the interparticle spacing decreases,

the longitudinal-mode redshift increases (Wang et al., 2010a).

When two nanoparticles come into close contact, their plasmon modes inter-

act electromagnetically, giving rise to hybridized plasmonic states that correspond

to the near-ﬁeld optical region, with an enhancement of electric ﬁeld at the parti-

cle surface. The strongest coupling occurs for longitudinal polarization, where the

symmetric bonding states have nonzero dipole moment and are referred to as bright

modes, since they are readily excited by incident photons. The antibonding states,

dark modes, possess higher energy and an antisymmetric electric ﬁeld with zero

dipole moment. Quadrupole and higher order modes of single particles are also

dark modes, as are propagating modes in nanoparticle chains. They interact only

3.4 Single, Plural, and Multiple Scattering 169

weakly with incident light but are of practical importance because of the possibility

of lossless waveguide transmission on a scale below the optical wavelength, useful

in surface-enhanced Raman spectroscopy and in biosensing and lasing applications.

A quantitative treatment is provided by the plasmon hybridization model, in

which the plasmon modes are treated as bonding and antibonding states of a one-

particle plasmon (Nordlander and Oubre, 2004). This model was used by Koh et al.

(2009) to describe spectra for a sub-nanometer probe traveling within and outside

spherical silver particles and pairs of particles (dimers). The modes can be displayed

in energy-ﬁltered images; in the limit of zero separation, they may differ by almost

a factor of 2 in energy, corresponding to the multipole and monopole modes of a

nanowire (Wang et al., 2009b).

Plasmon-resonance modes of small particles and arrays of particles are con-

veniently studied by STEM-EELS, as originally demonstrated by Batson (1982).

Recent improvements in instrumentation have made possible images with sub-

nanometer spatial resolution and sub-electron volt energy resolution. This capability

has led to impressive energy-ﬁltered images that display the geometry of the surface

plasmon modes within individual nanoparticles, and in arrays of particles or holes,

as discussed in Section 5.2.3.

3.4 Single, Plural, and Multiple Scattering

For a very thin specimen, the probability that a transmitted electron undergoes more

than one scattering event is low. Neglecting energy broadening by the spectrome-

ter system, the intensity J

(E) in the energy-loss spectrum t hen approximates to a

single-scattering distribution (SSD) or single-scattering proﬁle S(E):

(E) ≈ S(E) = I

t(dσ/dE) + I

(dP

/dE) (3.92)

where I

is the zero-loss intensity, approximately equal (because of the low scatter-

ing probability) to the total area I

under the loss spectrum. Here, n

is the number of

atoms (or molecules) per unit volume of the specimen and t is the specimen thick-

ness within the irradiated area. The energy-differential cross section per atom (or

molecule) dσ/dE is obtained by integrating the double-differential cross section,

given by Eq. (3.29)or(3.32), up to a scattering angle equal to the collection s emi-

angle β used when acquiring the spectrum. The last term in Eq. (3.92) represents the

intensity arising from surface-mode scattering. Integration over energy loss E gives

the total single-scattering intensity:

(β) = I

tσ (β) +I

(β) = I

[t/λ(β) +P

(β)] (3.93)

where σ (β) is an integral cross section, given by Eq. (3.57) for the case of volume

plasmon excitation.

170 3 Physics of Electron Scattering

3.4.1 Poisson’s Law

If inelastic scattering is viewed in terms of collisions that are independent events,

their occurrence should obey Poisson statistics: the probability that a transmitted

electron suffers n collisions is P

= (1/n!) m

exp(−m), where m is the mean num-

ber of collisions incurred by an electron t raveling through the specimen. Therefore,

we set m = t/λ, where λ is the average distance between collisions, the mean free

path for inelastic scattering. Sometimes t/λ is referred to as the scattering param-

eter of the specimen. P

is represented in the energy-loss spectrum by the ratio of

the energy-integrated intensity of n-fold scattering I

divided by the total integrated

intensity I

= I

= (1/n!)(t/λ)

exp(−t/λ) (3.94)

The variation of P

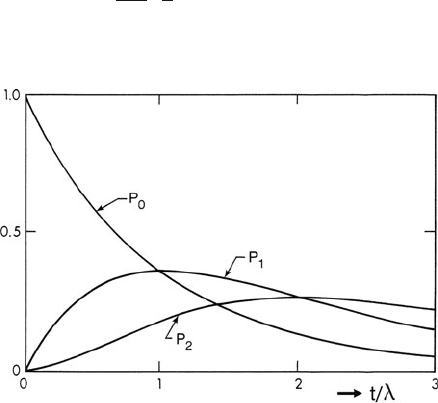
with scattering parameter is shown in Fig. 3.28. For a given order

n of scattering, the intensity is highest when t/λ = n. In the case of the unscattered

(n = 0) component (zero-loss peak), t he intensity is therefore a maximum at t = 0

and decreases exponentially with specimen thickness. For n = 0, Eq. (3.94)gives

t/λ = ln(I

) (3.95)

Equation (3.95) provides a simple way of measuring the thickness of a TEM

specimen from the energy-loss spectrum; see Section 5.1.

From Eq. (3.94), the average energy loss E per incident electron is

E=

∞



∞







exp(−t/λ) (3.95a)

Fig. 3.28 Probability of no

inelastic scattering (P

), of

single scattering ( P

) and of

double scattering (P

), as a

function of the scattering

parameter (t/λ)

3.4 Single, Plural, and Multiple Scattering 171

where the low-loss spectrum is approximated as a series of sharp peaks at multiples

of E

. In that case,

E=E

exp(−t/λ)

∞



(t/λ)

(n −1)!

= E

(3.95b)

Therefore there is a simple relationship between E, the average loss per incident

electron, and E

, which is the average energy loss per inelastic scattering event.

The following qualiﬁcations relate to Eq. (3.94), which is known as

Poisson’s law:

(1) Angles of scattering are assumed to be small, making the distances that elec-

trons travel through the specimen almost identical for the different orders n of

scattering.

(2) If several energy-loss processes (each characterized by a different mean free

path λ

) occur within the energy range over which the spectral intensity is inte-

grated in Eqs. (3.93) and (3.94), the number of scattering events is additive and

the effective scattering parameter is

t/λ =



/λ

(3.96)

If the transmitted electron passes through several layers, t

represents the

thickness of layer j, whereas if several scattering processes occur within a

single-layer specimen, each t

is equal to the specimen thickness.

(3) Although Eq. (3.94) refers to bulk processes, surface-mode scattering can be

included by using the surface-loss probability P

(see Section 3.3.5) as a sec-

ond scattering parameter. For normal incidence, P

is sufﬁciently small (<5%)

that second- and higher order surface scattering is negligible, but for reﬂection

at grazing incidence P

can exceed unity and multiple surface plasmon peaks

dominate the spectrum (see Fig. 3.26). For this situation, the validity of Poisson

statistics has been conﬁrmed experimentally (Schilling, 1976).

(4) Equation (3.94) is exact only if the specimen is of uniform thickness within

the area from which the s pectrum is recorded. The effect of thinner regions can

be visualized by imagining a hole to occur within the analyzed area; electrons

passing through the hole contribute to the zero-loss intensity I

but not to other

orders of scattering. Breakdown of Eq. (3.94) then leads to inaccuracy in the

removal of plural scattering by Fourier log deconvolution, as will be discussed

in Chapter 4.

(5) The use of Poisson statistics is justiﬁed if all scattering events contribute to the

measured intensities I

. However, the energy-loss spectrum is often recorded

with an angle-limiting aperture that accepts only a fraction F

(β) of the elec-

trons of a given order. In this situation, Eq. (3.94) retains its validity only if the

aperture factors obey the relationship

172 3 Physics of Electron Scattering

(β) = [F

(β)]

(3.97)

If Eq. (3.97) applies, substitution into Eq. (3.94) gives the measured intensity

as I

(β) = F

(β)

(

1/n!

)

(t/λ)

exp(−t/λ) I

(

1/n!

)

t/λ)

exp(−t/λ)

(

1/n!

)

t/λ)

exp[−t/λ(β)]I

, where λ(β) = λ/F

(β), so that

(β)/I

(β) = (1/n!)[t/λ(β)]

exp(−t/λ)





(1/n!)[t/λ(β)]

exp(−t/λ)

= (1/n!)[t/λ(β)]

exp[−t/λ(β)]

(3.98)

where I

(β) is the total measured intensity. In this case, Poisson’s law remains

valid, provided the mean free path λ is replaced by an aperture-dependent mean

free path λ(β) = λ/F

(β), inversely related to the integral cross section σ (β)

for scattering within the collection aperture:

λ(β) = [n

tσ (β)]

−1

(3.99)

where n

is the number of atoms per unit volume within the specimen. If

the angular distribution of scattering is Lorentzian with an abrupt cutoff at a

scattering angle θ

,Eq.(3.57) is valid and

(β) =

λ(β)

σ (β)

ln(1 +β

/θ

)

ln(1 +θ

/θ

)

(3.100)

As a result of this logarithmic dependence on the collection semi-angle, λ(β)

is somewhat longer than the mean free path λ for scattering through all angles.

However, to justify the validity of Eqs. (3.97) and (3.98), we need to examine

the angular distribution of plural scattering.

3.4.2 Angular Distribution of Plural Inelastic Scattering

In the case of double scattering, the intensity per unit solid angle dJ

/d is a two-

dimensional convolution of the single-scattering angular distribution. Using polar

coordinates to represent the radial component θ and the azimuthal component ϕ of

scattering angle, this convolution can be represented (Fig. 3.29)as

(θ)

d

∝





dσ (θ

)

d



dσ (θ

)

d



d

(3.101)

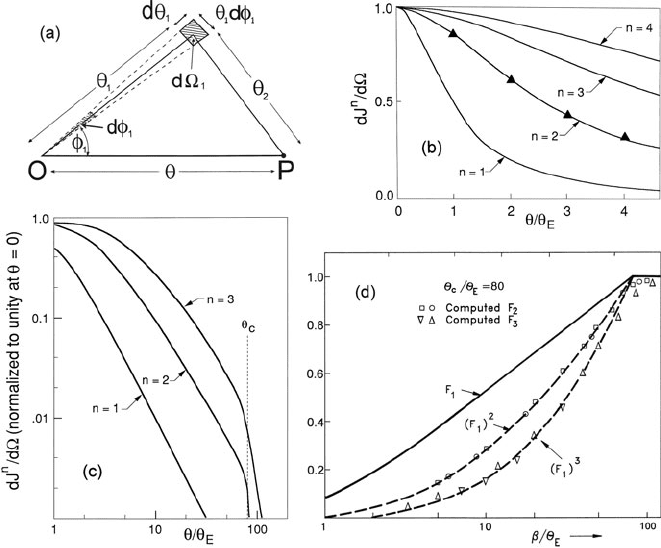
3.4 Single, Plural, and Multiple Scattering 173

Fig. 3.29 (a) Geometry of double scattering from O to P, showing scattering angles projected onto

a plane perpendicular to the optic axis. The individual scattering angles are θ

and θ

; the total

angular deﬂection after double scattering is θ.(b) Scattering per unit solid angle calculated for the

ﬁrst four orders; triangles represent double scattering obtained from Eq. (3.102). (c) Scattering per

unit solid angle, calculated up to high scattering angle and assuming an abrupt cutoff at θ

= 80 θ

(d) Fraction F

of inelastic scattering (or order n) collected by an aperture of semi-angle β.The

data points show F

and F

calculated using two different algorithms; dashed curves represent the

square and cube of F

. From Egerton and Wang (1990), copyright Elsevier

where the integration is over all solid angles 

. For a Lorentzian dσ/d with no

cutoff, the integration can be represented analytically:

/d ∝ θ

−1

{ln[1 −u

+uw −u/w]

−ln[(1 −2u

/v +w

)

1/2

+wu/v −u/w]}

(3.102)

where u = θ/θ

, v = 1 + π

/θ

, and w = (4 +θ

/θ

)

1/2

.Forθ

 θ  π,

Eq. (3.101) becomes

/d ∝ θ

−2

ln(θ/θ

) (3.103)

174 3 Physics of Electron Scattering

Therefore, at higher scattering angles the intensity falls off a little more slowly than

the θ

−2

dependence of single scattering (Fig. 3.29c).

A truncated Lorentzian angular distribution of single scattering can be speciﬁed

by introducing a function H(θ) that changes from 1 to 0 as θ passes through θ

,so

that Eq. (3.101) becomes

(θ)

d

∝



2π





H(θ

)

+θ



H(θ

)

+θ



θ dϕ

dθ

(3.104)

where θ

= θ

+ θ

− 2θθ

cos(ϕ

), applying the cosine rule to the vector triangle

in Fig. 3.29a. Equation (3.104) can be evaluated numerically, considerable compu-

tation being needed to achieve good accuracy. Exploiting the fact that the inelastic

scattering has axial symmetry, the double integral can be replaced by a single inte-

gral involving a Bessel function, the so-called Hankel transform (Bracewell, 1978),

with a reduction in computing time.

Extending Eq. (3.104), the intensity of n-fold scattering can be computed as

an n-fold convolution of dσ/d. Calculated angular distributions are shown in

Fig. 3.29b, c. Relative to the half-width θ

of single scattering, the half-widths of

the double, triple, and quadruple scattering distributions are increased by factors of

2.6, 5.1, and 7.5, respectively. Since some plural scattering intensity extends as far

as an angle nθ

, the “cutoff” at θ = θ

becomes more gradual as n increases.

To calculate the attenuation factor F

, the angular distribution of n-fold scattering

must be integrated up to an angle β and divided by the integral over all scattering

angles. Results for n = 2 and n = 3 are shown in Fig. 3.29d, in comparison to

the square and cube of F

(dashed curves). Although discrepancies are observable

close to θ

and at small angles, Eq. (3.97) is found to be accurate to within 3% for

β>15 θ

(Egerton and Wang, 1990; Su et al., 1992). Equation (3.97) has also

been inferred from the results of Monte Carlo calculations (Jouffrey et al., 1989)

and has been veriﬁed experimentally from deconvolution of plasmon-loss spectra

(see Fig. 4.2).

For double scattering (n = 2), Eq. (3.97) can be proved mathematically if we

take β  θ

, since if we assume F

= (F

)

, then

/d ∝ θ

−1

/dθ ∝ θ

−1

(dF

/dθ)

∝ θ

−1

d[ln

(θ/θ

)]/dθ ∝ θ

−2

ln(θ/θ

)

(3.105)

which is of the same form as Eq. (3.103), which is valid for θ>>θ

. Consequently,

Eq. (3.97) appears to be a property of the θ

−2

tail of the Lorentzian single-scattering

angular distribution.

3.4 Single, Plural, and Multiple Scattering 175

3.4.3 Inﬂuence of Elastic Scattering

So far, our discussion of angular distributions and plural scattering probabilities

has made no reference to elastic scattering, even though the probability of such

scattering is comparable to that of inelastic scattering; see page 126. In general, the

angular width of inelastic scattering is much less than that of elastic scattering (see

Section 3.2) and the collection semi-angle β used in spectroscopy is often less than

the characteristic angle θ

of elastic scattering or (for a crystalline specimen) the

scattering angle 2θ

of the lowest order diffraction spots. Under these conditions,

the t otal intensity I

(β) in the spectrum is reduced to a value that is considerably

below the incident beam intensity I, particularly for thicker specimens. Although

this reduction of intensity is the most important effect of elastic scattering on the

energy-loss spectrum, we will now consider its effect on the relative intensities of

the different orders of inelastic scattering recorded by a spectrometer.

In an amorphous material, elastic and inelastic scattering are independent and

both are governed by Poisson statistics, so the joint probability of m elastic and n

inelastic events is

P(m, n) = (x

/m!)(t/λ

)

/n!)(t/λ

)

(3.106)

where x

= exp(−t/λ

) and x

= exp(−t/λ

); λ

and λ

are the mean free paths

for elastic and inelastic scattering through all angles. If a fraction F(m, n)ofthe

electrons passes through a collection aperture of semi-angle β, the recorded zero-

loss component I

(β) for an incident beam intensity I is given by

(β)/I =

∞



P(m,0)F(m,0)= x

∞



(1/m!)(t/λ

)

(β) (3.107)

Here, x

represents the unscattered electrons and F

(β)isthefractionofm-fold

purely elastic scattering that passes through the aperture. Calculations (Wong and

Egerton, 1995) based on the Lenz model suggest that the m-fold elastic scattering

distribution approximates to a broadened single-scattering angular distribution with

replaced by (0.7 +0.5m) θ

,sothatEq.(3.6) becomes, for m > 1

(β) ≈ [1 +(0.7 +0.5m)

/β

]

−1

(3.108)

The inelastic intensity I

(β) transmitted through the aperture, integrated over all

orders of scattering, is given by

(β)/I =

∞

m=0

∞

n=1

P(n, m) F(n, m)

= x

∞

n=1

(1/n!)(t/λ

)

(β) +

∞

m=1

∞

n=1

P(n, m)F(m, n)

(3.109)

176 3 Physics of Electron Scattering

(β) is the fraction of inelastic scattering that passes through the aperture, previ-

ously denoted F

(β), and the ﬁnal term in Eq. (3.109) represents electrons that have

been scattered both elastically and inelastically. Calculations (Wong and Egerton,

1995) of the angular distribution of this “mixed” scattering, based on Lenz model

single-scattering distributions, indicate that the corresponding aperture function can

be approximated by a simple product:

F(m, n) ≈ F

(β)F

(β) (3.110)

Most likely, Eq. (3.110) results from the fact that the elastic and inelastic scattering

have very different angular widths. Now Eq. (3.109) can be rewritten, making use

of Eqs. (3.107) and (3.97), as

(β)/I = x

∞

n=1

(1/n!)(t/λ

)

(β)



1 +

∞

m=1

(t/λ

)

(β)



= [I

(β)/I)][exp(F

t/λ

) −1]

(3.111)

Writing the total intensity recorded through the aperture as I

(β) = I

(β)+I

(β) and

deﬁning t/λ

(β) = F

(t/λ

) as before, Eq. (3.111) becomes

t/λ

(β) = ln[I

(β)/I

(β)] (3.112)

which is the same as Eq. (3.95), derived previously without considering elastic scat-

tering. This equation, which is used for measuring specimen thickness (Section 5.1),

can therefore be justiﬁed mathematically on the basis of angular distributions (of

elastic and inelastic scattering) that are found to be good approximations for amor-

phous specimens (Wong and Egerton, 1995). Experimentally, Eq. (3.112) has been

veriﬁed to within 10% for t/λ

< 5 in amorphous, polycrystalline, and single-crystal

specimens (Hosoi et al., 1981; Leapman et al., 1984a).

Elastic scattering has a greater inﬂuence on the recorded intensity of inner-shell

inelastic scattering (whose angular width is often comparable to that of elastic scat-

tering), as discussed in Section 4.3.2.2. In crystalline specimens, additional effects

occur as a result of channeling; see Section 3.1.4.

3.4.4 Multiple Scattering

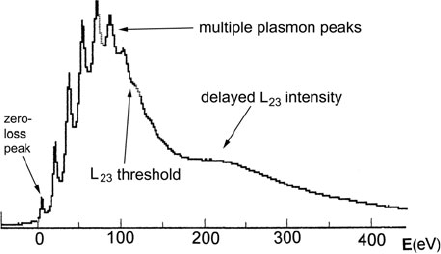
For relatively thick specimens (t/λ > 5), individual peaks may not be visible in

the l oss spectrum; multiple outer- and inner-shell processes combine to produce a

Landau distribution (Whelan, 1976;Reimer,1989) that is broadly peaked around

an energy loss of some hundreds of electron volts; see Fig. 3.30. The position of

the maximum (the most probable energy loss) is roughly proportional to specimen

thickness (Perez et al., 1977; Whitlock and Sprague, 1982) and is very approxi-

mately (t/λ)E

, where E

is the energy of the main peak in the single-scattering

distribution. This multiple scattering behavior is sometimes called straggling.

3.4 Single, Plural, and Multiple Scattering 177

Fig. 3.30 Energy-loss

spectrum of a thick region of

crystalline silicon

(t/λ = 4.5), showing multiple

plasmon peaks superimposed

on a Landau background and

followed by an extended and

broadened L-edge

When the number n of events is large, the angular distribution of scattering tends

toward a Gaussian function, a consequence of the central limit theorem (Jackson,

1975). The mean-square angular deﬂection is n

, where

is the mean-square

angle for single scattering, given by Eq. (3.54) for the case of a truncated Lorentzian

angular distribution of single scattering.

3.4.5 Coherent Double-Plasmon Excitation

A fast electron traveling through a solid can in principle lose a characteristic amount

of energy equal to 2 ω

in a single scattering event. In accordance with Eq. (3.94),

the intensity at an energy loss E = 2 ω

should therefore be

= I

[(t/λ

)

/2 + t/λ

] (3.113)

where the ﬁrst term represents the incoherent production of two plasmons in sep-

arate scattering events (in accordance with Poisson’s law) and the second term

represents coherent double-plasmon excitation, characterized by a mean free path

. As seen from Eq. (3.113), the coherent contribution is fractionally greater in the

case of very thin specimens. It should be visible directly if the energy-loss spectrum

is deconvolved to remove the incoherent plural scattering.

Based on a free-electron model, Ashley and Ritchie (1970) deduced that the rel-

ative probability P

rel

of the double process is proportional to the ﬁfth power of the

cutoff wavevector q

. Taking q

≈ ω

their f ormula becomes

rel

= λ

/λ

≈ 0.013r

(3.114)

where r

is the radius of a sphere containing one free electron, divided by the Bohr

radius a

. The lowest free-electron density (corresponding to r

= 5.7) occurs

in cesium, giving P

rel

= 0.34. For aluminum, Eq. (3.114) yields r

= 2.0 and