Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

138 3 Physics of Electron Scattering

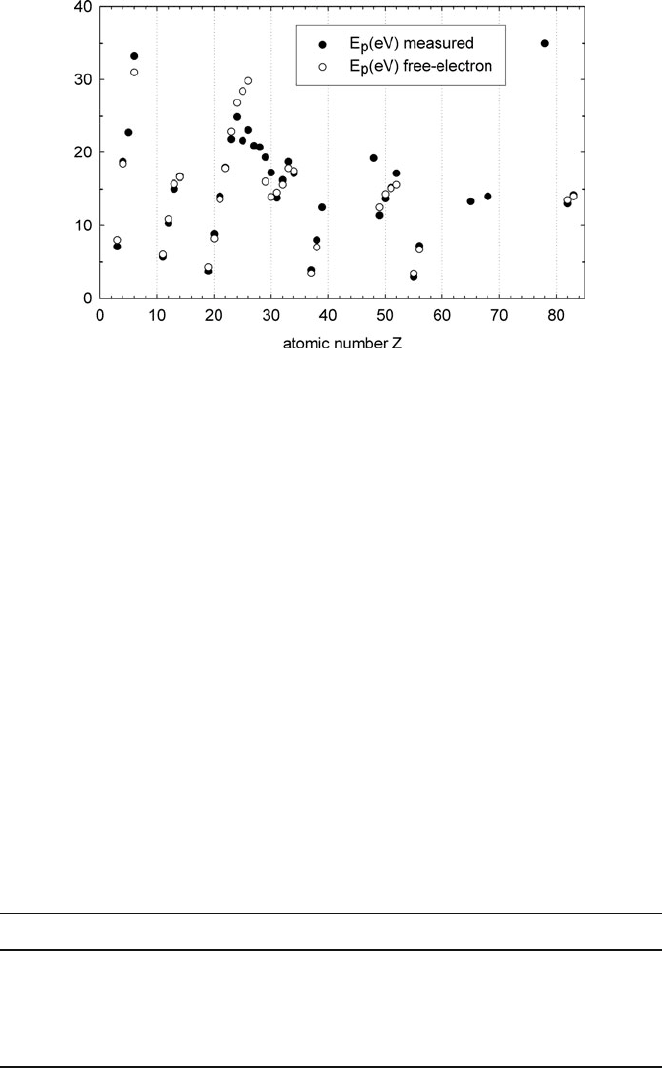
Fig. 3.12 Energy of the main valence-loss peak, as measured by EELS (ﬁlled circles)andas

predicted by the free-electron formula, Eq. (3.41) with m = m

(hollow circles). Agreement is

good except for transition metals and rare earths, where d- and f-electrons contribute to ionization

edges with relatively low energy and high cross section

such as silicon and germanium (Hinz and Raether, 1979). Even with m = m

Eq. (3.41) provides fairly accurate values for the energy of the main peak in the

energy-loss spectrum of many solids, taking n as the density of outer-shell electrons;

see Fig. 3.12 and Table 3.2.

The r elaxation time τ represents the time for plasma oscillations to decay in

amplitude by a factor exp(−1) = 0.37. The number of oscillations that occur within

this time is ω

τ/(2π) = 0.16 (E

). Using experimental values of E

and E

this number turns out to be 4.6 for aluminum, 2.3 for sodium, 0.7 for silicon, and

0.4 for diamond, so the plasma oscillations tend to be highly damped, to a degree

that depends on the band structure of the material (see Section 3.3.2).

The double-differential cross section for plasmon scattering is obtained by

substituting Eq. (3.43) into Eq. (3.32), giving

Table 3.2 Plasmon energy E

of several materials that show sharp peaks in the low-loss spectrum,

calculated using the free-electron formula and compared with measured values. The characteristic

angle θ

, cutoff angle θ

[estimated from Eqs. (3.50)and(3.51)] and the plasmon mean free path

[Eq. (3.58)] are for 100-keV incident electrons

Material E

(calc) (eV) E

(expt) (eV) E

(eV) θ

(mrad) θ

(mrad) λ

(calc) (nm)

Li 8.0 7.1 2.3 0.039 5.3 233

Be 18.4 18.7 4.8 0.102 7.1 102

Al 15.8 15.0 0.53 0.082 7.7 119

Si 16.6 16.5 3.7 0.090 6.5 115

K 4.3 3.7 0.3 0.020 4.7 402

3.3 Excitation of Outer-Shell Electrons 139

ddE

≈





E(E

−E

)

+(E E

)



+θ



(3.43b)

This expression can be integrated over scattering angle to give an energy-differential

cross section for all scattering up to an angle β, on the assumption that the integra-

tion remains within the dipole region (β<θ

, where θ

is the plasmon cutoff angle

discussed below):

dσ (β)

≈



πa



E(E

−E

)

+(E E

)

ln(1 +β

/θ

) (3.43c)

It is also useful to integrate Eqs. (3.43b) and (3.43c) over energy loss, but since

the variable E occurs also in the θ

term, a simple analytic expression is possible

only for zero damping (E

= 0). In that case, the middle term in these equations

becomes a delta function: (π/2)E

δ(E −E

), giving

dσ

d

≈

2πa



+θ



(3.44)

(β) ≈

ln(1 +β

/θ

) (3.44a)

where θ

= E

/(γ m

)orθ

≈ E

/2E

within 10% accuracy for E

< 120 keV.

In the case of a broad plasmon peak, where E

≈ 0 is not a good approxima-

tion, the integration over energy loss must be done numerically. For the Drude model

E-dependence, Eq. (3.44a) is found to overestimate the cross section, by about 1%

for aluminum (E

≈ 0.5 eV) and about 6% for silicon (E

= 3.2 eV). Other

cases can be investigated using the D

RUDE program, discussed in Appendix B.

3.3.1.2 The Plasmon Wake

When a stationary charged particle is placed in a conducting medium, electrostatic

forces cause the electron density to readjust around the particle in a spherically

symmetric manner (screening by a “correlation hole”), reducing the extent of the

long-range Coulomb ﬁeld and minimizing the potential energy. When the parti-

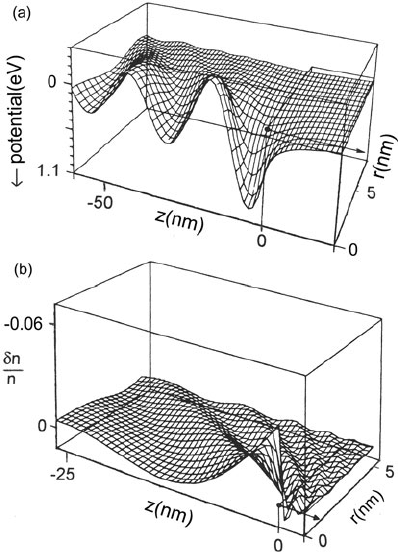
cle is moving at a speed v, an additional effect occurs as illustrated in Fig. 3.13

(Echenique et al., 1979). Behind the particle, the potential and electron density

oscillate at the plasmon frequency (ω

rad/s), corresponding to spatial oscillation

with a wavelength λ

= 2πv/ω

. These oscillations also spread laterally, deﬁning

a cone of semi-angle α ≈ v

/v, where v

is the Fermi velocity in the medium. For a

100-keV electron, this cone is narrow (α<1

◦

), as indicated by the different length

scales for the radial and longitudinal distances in Fig. 3.13.

Garcia de Abajo and Echenique (1992) showed that formation and destruction

of the wake occurs within distances of approximately λ

/4 = (π/2)(v/ω

)ofthe

entrance and exit surfaces of the specimen; the parameter v/ω

is the same as Bohr’s

140 3 Physics of Electron Scattering

Fig. 3.13 (a) Response of medium (plasmon energy = 25 eV) to a moving charged particle,

depicted in terms of the scalar potential calculated by Echenique et al. (1979), with axes relabeled

to correspond to the case of a 100-keV electron. Oscillations along the z-axis (direction of electron

travel) represent the wake potential, which gives rise to plasmon excitation. (b) Corresponding

fractional change in electron density. This ﬁgure also reveals bow waves that start ahead of the

particle and extend laterally as a paraboloidal pattern; they arise from small impact parameter col-

lisions that generate single-electron excitations within the solid. For 100-keV electrons, the bow

waves would be more closely spaced than shown, since their wavelength scales inversely with par-

ticle speed. Based on Echenique et al. (1979), copyright American Physical Society. Available at

http://link.aps.org/abstract/PRB/v20/p2567

delocalization distance b

max

; see Section 3.11.ForE

= 15 eV and E

= 100 keV,

v/ω

≈ 7.2 nm. Because of this “dead layer” beneath the surface, the probability

of bulk plasmon generation is reduced (the so-called begrenzungs effect), in com-

pensation for the surface plasmon excitation that occurs at each surface; see also

Fig. 3.25.

Batson (1992b) pointed out that the charge-density and electric ﬁeld ﬂuctuations

in the plasmon wake can excite electron transitions in the specimen, after the fast

electron has passed, but that these single-electron excitations contribute to damping

of the plasmon rather than additional energy loss. Batson and Bruley (1991) and

Batson (1993c) have suggested that the form of the plasmon wake might account

3.3 Excitation of Outer-Shell Electrons 141

for s mall differences in ﬁne structure between x-ray absorption and K-loss edges of

diamond and other insulators.

3.3.1.3 Plasmon Dispersion: The Lindhard Model

Equation (3.43) describes the energy dependence of the loss spectrum but applies

only to small scattering vectors q (dipole region). The jellium model was ﬁrst

extended to higher q by Lindhard (1954), using the random-phase approximation

(Sturm, 1982) and assuming Fermi statistics, but neglecting spin exchange and cor-

relation effects arising from Coulomb interaction between the oscillating electrons.

The Lindhard model leads to analytical expressions for ε(q, E) and Im(−1/ε) (Tung

and Ritchie, 1977; Schnatterly, 1979; Schattschneider and Jouffrey, 1994). In the

limit  = 0, corresponding to completely free electrons, the plasmon energy E

(q)

at which ε

passes through zero is given by the equations

(q) = E

+α (

) q

(3.45)

α = (3/5)E

(3.46)

where E

is the Fermi energy. Equation (3.45)isadispersion relation for the

plasmon, α being the dispersion coefﬁcient. The increase i n plasmon energy with

increasing q (i.e., increasing scattering angle) can be seen in Fig. 3.14, where the

Fig. 3.14 Energy-loss function Im(−1/ε) computed for silicon using t he Lindhard model. Vertical

arrows represent the volume plasmons. The plasmon dispersion curve enters the region of kine-

matically allowed single-electron excitation at point P, which deﬁnes the cutoff wavevector q

.For

q >> q

, the single-electron peak is reduced in intensity and is known as the Bethe ridge. From

Walther and Cohen (1972), copyright American Physical Society. Available at http://link.aps.org/

abstract/PRB/v5/p3101

142 3 Physics of Electron Scattering

plasmon peaks are represented by delta functions (vertical arrows) since damping

has been neglected.

The Lindhard model can be extended to include plasmon damping (Mermin,

1970; Gibbons et al., 1976) and insulating materials whose electron distribution

is characterized by an energy gap (Levine and Louie, 1982). It is also possible to

avoid the random-phase approximation (RPA) and include electron correlation, as

ﬁrst done by Nozieres and Pines (1959), who obtained a dispersion relation similar

to Eq. (3.45) but with the dispersion coefﬁcient given by

α =



1 −







(3.47)

In the case of aluminum, α is reduced by 11% from its RPA value (0.45), giv-

ing improved agreement with most measurements: for example, α = 0.38 ± 0.02

(Batson and Silcox, 1983).

The q-dependence is sometimes used to test the character of a valence-loss peak

(Crecelius et al., 1983). If the measured value of the dispersion coefﬁcient is com-

parable to the RPA value given by Eq. (3.46), collective behavior is suspected; if α

is close to zero, an interband transition may be involved.

Unless the energy-loss spectrum is recorded using a sufﬁciently small collection

aperture (semi-angle  θ

1/2

), contributions from different values of q cause a slight

broadening and upward shift of the plasmon peak.

3.3.1.4 Critical Wavevector

Above a certain wavevector q

, the plasma oscillations in a “free-electron gas” are

very heavily damped because it becomes possible for a plasmon to transfer all of

its energy to a single electron, which can then dissipate the energy by undergoing

an interband transition. Such an event must satisfy the usual conservation rules; if

an energy E and momentum  q aretobetransferredtoanelectronofmassm

that initially had a momentum  q

, conservation of both energy and momentum

requires

E = (

/2m

)(q +q

)

−(

/2m

= (

/2m

)(q

+2q ·q

) (3.48)

The minimum value of q that satisﬁes Eq. (3.48) corresponds to the situation where

is parallel to q and as large as possible, namely, q

= q

, where q

is the Fermi

wavevector. Denoting this minimum value of q as q

and substituting for E = E

(q)

using Eq. (3.45)gives

+α(

= (

/2m

)(q

+2q

) (3.49)

If the dispersion coefﬁcient α is not greatly different from 0.5, the quadratic terms

on both sides of Eq. (3.49) almost cancel and to a rough approximation

3.3 Excitation of Outer-Shell Electrons 143

 m

/(

) = E

/(v

) (3.50)

where v

is the Fermi velocity. Equation (3.50) is equivalent to ω

/q  v

; in other

words, energy transfer becomes possible when the phase velocity of the plasmon

falls to a value close to the velocity of electrons at the Fermi surface. More precisely,

is deﬁned by intersection of the curves representing Eqs. (3.45) and (3.48) with

= q

, i ndicated by the point P in Fig. 3.14.

A jellium model therefore predicts that inelastic scattering due to plasmon exci-

tation should fall abruptly to zero above a critical (or cutoff) angle θ

that is related

to the critical wavevector q

≈ k

(θ

+θ

) ≈ k

(3.51)

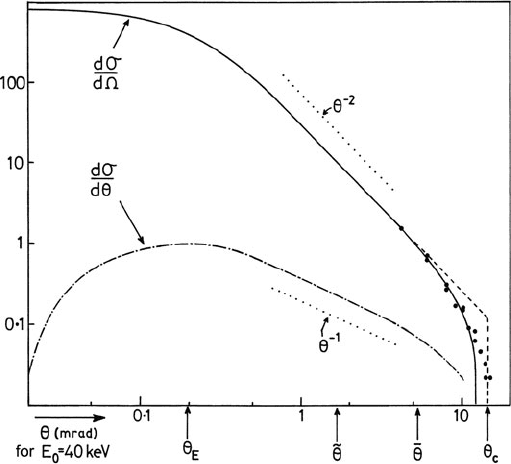
A more sophisticated calculation based on Hartree–Fock wavefunctions (Ferrell,

1957) predicts a gradual cutoff described by a function G(q, q

) that falls (from

unity) to zero at q = 0.74 q

, in somewhat better agreement with experimental

data; see Fig. 3.15. In fact, experimental evidence suggests that inelastic scattering is

partly collective in nature at wavevectors considerably above q

(Batson and Silcox,

1983).

Fig. 3.15 Angular dependence of the differential cross section dσ/d for plasmon scattering

as calculated by Ferrell (solid curve) and using a sharp cutoff approximation (dashed line).

Experimental data of Schmüser (1964) for aluminum and 40-keV incident electrons are indicated

by the solid circles. Also shown are the characteristic, median, mean, and cutoff angles, calculated

using Eqs. (3.51), (3.52), (3.53), (3.54), (3.55), and (3.56)

144 3 Physics of Electron Scattering

3.3.1.5 Mean, Root-Mean-Square, and Median Scattering Angles

The mean scattering angle

θ associated with plasmon scattering can be deﬁned as

θ =





dσ

dθ



dθ





dσ

dθ

dθ =





dσ

d



d





dσ

d

d (3.52)

where the integration is over all scattering angle θ or all solid angle . If the dif-

ferential cross section has a Lorentzian angular dependence with an abrupt cutoff at

θ = θ

, the approximation d = 2π (sin θ) dθ ≈ (2πθ) dθ (since θ

 1) leads to

θ =



dθ

+θ



θc



θdθ

+θ

−θ

arctan(θ

/θ

)

ln[1 +(θ

/θ

)

]

(3.53)

with θ

= E

,asinEq.(3.44). Similarly, a mean-square angle can be

evaluated as



= θ

/ ln(1 +θ

/θ

) −θ

(3.54)

The root-mean-square angle θ (rms) is the square root of

and is used in the

analysis of the angular distribution of multiple scattering.

A median scattering angle

θ can also be deﬁned, such that half of the scattering

occurs at angles less than

θ:



dσ

dθ





dσ

dθ

dθ =

(3.55)

Making a low-angle approximation, as above, gives

θ = θ

(θ

/θ

−1)

1/2

≈ (θ

)

1/2

(3.56)

For 100-keV incident electrons, θ

/θ

≈ v/v

≈ 100 in a typical material (see

Table 3.2), giving

θ ≈ 22θ

and

θ ≈ 10θ

. These average scattering angles are at

least an order of magnitude larger than θ

, reﬂecting the 2π sin θ weighting factor

that relates d and dθ and the wide “tails” of the Lorentzian angular distribution,

compared to a Gaussian function of equal half-width.

Besides being the half-width of the differential cross section dσ/d, which

represents t he amount of scattering per unit solid angle, θ

is the most probable

scattering angle, corresponding to the maximum in dσ/dθ ; see Fig. 3.15.

Equations (3.53), (3.54), (3.55), and (3.56) apply to any scattering with a

Lorentzian angular distribution that terminates at a cutoff angle θ

. They are use-

ful approximations for single-electron excitation (including inner-shell ionization)

at an energy loss E, with θ

replaced by the appropriate characteristic angle

3.3 Excitation of Outer-Shell Electrons 145

= E/(γ m

) and the Bethe ridge angle θ

≈ (E/E

)

1/2

≈ (2θ

)

1/2

used as

the cutoff angle; see Section 3.6.1. The same equations may also be applicable to

total-inelastic scattering (integrated over all energy loss), replacing θ

and

setting θ

≈ θ

= 1/(k

), the effective cutoff angle beyond which dσ/d changes

from a θ

-2

to a θ

-4

angular dependence; see Section 3.2.1.

3.3.1.6 Plasmon Cross Section and Mean Free Path

Provided β<θ

, the free-electron approximation of Eq. ( 3.44a)givestheintegral

cross section per atom (or per molecule) as follows:

(β) =

ln(1 +β

/θ

)

≈

ln(β/θ

)

(3.57)

where n

is the number of atoms (or molecules) per unit volume and the approxima-

tioninEq.(3.57) applies to the case β  θ

. An inverse measure of the amount of

scattering below the angle β is the mean free path λ

(β) = [n

(β)]

−1

, given by

(β) =

ln(1 +β

/θ

)

≈

γθ

ln(β/θ

)

(3.58)

These free-electron formulas give reasonably accurate values for “free-electron”

metals such as aluminum (Fig. 3.16a) but apply less well to transition metals

(Fig. 3.9), where single-electron and core-level transitions considerably modify the

energy-loss spectrum.

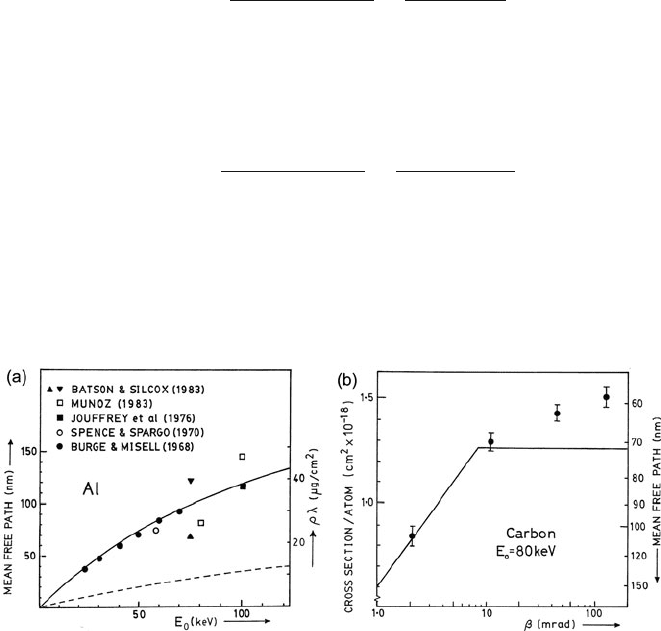
Fig. 3.16 (a) Incident energy dependence of mean free path for valence excitation, as predicted

by free-electron theory, Eq. (3.58) with β = θ

= 7.7 mrad, and as determined from EELS mea-

surements. Batson and Silcox (1983) give two values, t he lower one including the plasmon peak

background due to single-electron transitions. (b) Collection-angle dependence of mean free path,

as predicted by Eq. (3.58) with β = θ

= 8.5 mrad and from EELS measurements (Egerton, 1975)

including all energy losses up to 50 eV

146 3 Physics of Electron Scattering

Estimates of the total plasmon cross section and mean free path are obtained by

substituting β = θ

in Eqs. (3.57) and (3.58), implying a sharp cutoff of intensity at

θ = θ

. For 100-keV incident electrons, λ

is of the order of 100 nm (see Table 3.2,

page 138). In practice, single-electron excitation causes some inelastic scattering to

occur above θ

, so the measured inelastic mean free path decreases by typically 10–

20% between β ≈ 10 mrad (a typical plasmon cutoff angle) and β ≈ 150 mrad (the

maximum collection angle possible in a typical TEM, limited by the post-specimen

lenses); see Figs. 3.16b and 5.2d.

3.3.2 Single-Electron Excitation

As discussed in the preceding section, the plasmon model accounts for the major

features of the low-loss spectrum of materials such as Na, Al, and Mg where motion

of the conduction electrons is relatively unaffected by the crystal lattice. The plas-

mon peaks are particularly dramatic in the case of alkali metals, where E

falls

below the ionization threshold (Fig. 3.10), giving low plasmon damping.

In all materials, however, there exists an alternative mechanism of energy loss,

involving the direct transfer of energy from a transmitted electron to a single atomic

electron within the specimen. This second mechanism can be regarded as compet-

ing with plasmon excitation in the sense that the total oscillator strength per atom

must satisfy the Bethe sum rule, Eq. (3.34). The visible effects of single-electron

excitation include the addition of ﬁne structure to the energy-loss spectrum and a

broadening and/or shift of the plasmon peak, as we now discuss.

3.3.2.1 Free-Electron Model

In Section 3.3.1,Eq.(3.48) referred to the transfer of energy from a plasmon to a

single atomic electron, but this same equation applies equally well to the case where

the energy E is supplied directly from a fast electron. By inspecting Eq. (3.48) it can

be seen that, for a given value of q, the maximum energy transfer E(max) occurs

when q

is parallel to q and as large as possible (i.e., q

= q

) so that

E(max) = (

/2m

)(q

+2qq

) (3.59)

The minimum energy loss E(min) corresponds to the situation where q

is antipar-

allel to q and equal to q

,giving

E(min) = (

/2m

)(q

−2qq

) (3.60)

Within the region of q and E deﬁned by Eqs. (3.59) and (3.60) (the shaded area in

Fig. 3.17), energy loss by single-electron excitation is kinematically allowed in the

free-electron approximation. The Lindhard model (Section 3.3.1) predicts the prob-

ability of such transitions and shows (Fig. 3.14) that they occur within the expected

region, but mainly at higher values of q.Atlargeq,Im[−1/ε] becomes peaked

around E = (

/2m

, as predicted by Bethe theory (see later, Fig. 3.36).

3.3 Excitation of Outer-Shell Electrons 147

Fig. 3.17 Energy loss as a

function of scattering vector,

showing the region deﬁned by

Eqs. (3.59)and(3.60), over

which single-electron

excitation is allowed

according to the jellium

model. Also shown (dashed)

is the plasmon dispersion

curve E

(q). The horizontal

arrow indicates momentum

transfer from the lattice,

resulting in damping of the

plasmon

In terms of particle concepts, large q corresponds to a collision with small impact

parameter; if the incident electron passes sufﬁciently close to an atomic electron,

the latter can receive enough energy to be excited to a higher energy state (single-

electron transition). In contrast, atomic electrons further from the path of the fast

electron may respond collectively and share the transferred energy.

The relationship between collective and single-particle effects is further illus-

trated in the plasmon pole (or single-mode) model developed by Ritchie and Howie

(1977). In their treatment, two additional terms occur in the denominator of Eq.

(3.43), resulting in a dispersion relation

≡ [E

(q)]

= E

+(3/5)(q/q

)

+

/4m

(3.61)

which for small q reduces to the plasmon dispersion relation, Eqs. (3.45) and (3.46),

and at large q to the energy–momentum relation (E = 

/2m

) for an isolated

electron (dashed line in Fig. 3.17). An expression for the energy-loss function can

also be derived; neglecting plasmon damping, the differential cross section takes the

form (Ritchie and Howie, 1977)

dσ

d

−2E

)

1/2

2π

≈

2π



+θ



(3.62)

with θ

= E

/(γ m

). Equation (3.62) becomes equivalent to the plasmon formula,

Eq. (3.44), at small scattering angles. At large q, where the momentum is absorbed

mainly by a single electron that receives an energy much larger than its binding

energy, Eq. (3.62) becomes the Rutherford cross section for scattering from a free

electron: Eq. (3.3) with Z = 1.