Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

108 2 Energy-Loss Instrumentation

solution is to increase the probe diameter as the magniﬁcation is lowered, although

this may still leave some of the specimen unirradiated because the probe is circular

and the pixels are square. An equally good solution, in the case of a digitally gener-

ated scan, is to use sub-pixel scanning: for an image having N×N pixels, waveforms

whose frequency is N times larger and amplitude N times smaller are added to the

line and frame scans. The very small probe is then scanned in a small square raster,

covering each pixel area, so that severe undersampling of the specimen is avoided.

2.6.6 Z-Contrast and Z-Ratio Imaging

The scanning-transmission electron microscope has the advantage of being able

to efﬁciently collect electrons that are scattered through large angles, by use of a

high-angle annular dark-ﬁeld (HAADF) detector. This high-angle elastic scattering

approximates to Rutherford elastic scattering (Section 3.1.2), which ideally has a

dependence on atomic number Z, although slightly lower exponents are com-

mon (Section 3.1.6). The STEM therefore provides Z-contrast images, useful for

imaging clusters of heavy atoms on a lower-Z substrate (e.g., catalyst s tudies) and

atomic columns in crystalline specimen (Pennycook and Jesson, 1991; Krivanek

et al., 2010). Channeling of the incident electrons limits the lateral spreading of

the beam in a crystalline specimen, allowing core-loss spectroscopy to identify the

atomic number of each column (Browning et al., 1993b, 1999; Pennycook et al.,

1995a; Varela et al., 2004). This spectroscopy can be precisely simultaneous with

the structural imaging because it makes use of electrons that pass through the central

hole of the HAADF detector, as in Fig. 2.35.

Z-ratio imaging refers to a technique ﬁrst used by Crewe et al. (1975)todis-

play images of single atoms of Hg and U on a thin-carbon (<10 nm) support

ﬁlm. The ADF signal I

was divided by the total-inelastic signal I

recorded

Fig. 2.35 Z-contrast imaging

in STEM mode. The inner

radius of the annular detector

subtends a semi-angle β at

the specimen, the outer radius

being considerably larger. An

electron spectrometer

separates the inelastic and

unscattered electrons

2.6 Energy-Selected Imaging (ESI) 109

through a spectrometer, using a wide energy-selecting slit that simply eliminated

the unscattered component I

; see Fig. 2.35. A single-channel detector, such as a

scintillator/PMT combination, is sufﬁcient to measure I

. Because variations in mass

thickness of the support contribute almost equally to I

and I

, their unwanted effect

largely disappears in the image formed from the ratio R = I

. Taking a ratio also

cancels any ﬂuctuations in probe current but does involve some increase in noise,

particularly if the specimen is very thin.

Because of its relatively broad angular distribution (Section 3.2.1), elastic scatter-

ing provides the main contribution to I

, whereas the main contribution to I

comes

from electrons that suffer only inelastic scattering. If the specimen is amorphous

and very thin, the elastic and inelastic scattering are both proportional to specimen

thickness and to the appropriate atomic cross sections σ

and σ

. Assuming that all

elastic scattering is recorded by the dark-ﬁeld detector and all inelastic scattering is

captured by the spectrometer, the ratio signal is

R = I

= σ

/σ

= λ

/λ

(2.54)

where λ

and λ

are mean free paths for elastic and inelastic scattering. The inten-

sity in the ratio image is then proportional to the l ocal value of the elastic/inelastic

scattering ratio, which in theory and in practice (Section 3.2.1) is proportional to

atomic number Z.

In the case of specimens that are thicker than about λ

/2, the dark-ﬁeld and

inelastic signals are given more accurately (Lamvik and Langmore, 1977; Egerton,

1982c)by

= I[1 −exp(−t/λ

)] (2.55)

= I exp(−t/λ

)[1 −exp(−t/λ

)] (2.56)

where I is the i ncident beam current and t is the local thickness of the specimen. The

exponential functions in Eqs. (2.55) and (2.56) occur because of plural scattering, as

a result of which neither I

nor I

is proportional to specimen thickness. For t/λ

< 1,

this nonlinearity can be removed by digital processing (Jeanguillaume et al., 1992).

For t/λ

>1,I

reaches a maximum and then decreases with increasing thickness,

as many of the inelastically scattered electrons also undergo elastic scattering and

therefore contribute to I

rather than to I

Z-ratio imaging has been used to increase the contrast of thin (30-nm) sections

of stained and unstained tissues (Carlemalm and Kellenberger, 1982; Reichelt et al.,

1984). If the sample is crystalline and the ADF detector accepts medium-angle scat-

tering, both the elastic and inelastic images are strongly inﬂuenced by diffraction

contrast, which may increase rather than cancel when the ratio is taken (Donald and

Craven, 1979).

Chapter 3

Physics of Electron Scattering

It is convenient to divide the scattering of fast electrons into elastic and inelastic

components that can be distinguished on an empirical basis, the term elastic mean-

ing that any energy loss to the sample is not detectable experimentally. This criterion

results in electron scattering by phonon excitation being classiﬁed as elastic (or

quasielastic) when measurements are made using an electron microscope, where

the energy resolution is rarely better than 0.1 eV. The terms nuclear (for elastic scat-

tering) and electronic (for inelastic scattering) would be more logical but are not

widely used.

3.1 Elastic Scattering

Elastic scattering is caused by interaction of incident electrons with the electrostatic

ﬁeld of atomic nuclei. The atomic electrons are involved only to the extent that

they terminate the nuclear ﬁeld and therefore determine its range and magnitude.

Because a nucleus is some thousands of times more massive than an electron, the

energy transfer involved in elastic scattering is usually negligible. However, for the

small fraction of electrons that are scattered through large angles (up to 180

◦

), the

transfer can amount to some tens of electron volts, as evidenced by the occurrence

of displacement damage and electron-induced sputtering at high incident energies

(Jenkins and Kirk, 2001).

Although not studied directly by electron energy-loss spectroscopy, elastic

scattering is relevant for the following reasons:

1. Electrons can undergo both elastic and inelastic interactions within the sample,

so elastic scattering modiﬁes the angular distribution of the inelastically scattered

electrons.

2. In a crystalline material, elastic scattering can redistribute the electron ﬂux

(current density) within each unit cell and change the probability of localized

inelastic scattering (see Section 3.1.4).

3. The ratio of elastic and inelastic scattering can provide an estimate of the local

atomic number or chemical composition of a specimen (Sections 2.6.6 and

5.4.1).

111

R.F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope,

DOI 10.1007/978-1-4419-9583-4_3,



Springer Science+Business Media, LLC 2011

112 3 Physics of Electron Scattering

3.1.1 General Formulas

A quantity of basic importance in scattering theory is the differential cross section

dσ/d, representing the probability of an incident electron being scattered (per unit

solid angle ) by a given atom. For elastic scattering, one can write

dσ/d =

(3.1)

where f is a (complex) scattering amplitude or atomic scattering factor, which is

a function of the scattering angle θ or scattering vector q. The phase component

of f is important in high-resolution phase-contrast microscopy (Spence, 2009)but

for the calculation of scattered intensity only the amplitude is required, as implied

in Eq. (3.1). Within the ﬁrst Born approximation (equivalent to assuming only sin-

gle scattering within each atom), f is proportional to the three-dimensional Fourier

transform of the atomic potential V(r).

Alternatively, the differential cross section can be expressed in terms of an elastic

form factor F(q):

dσ

d

F(q)

Z −f

(q)

(3.2)

Here a

= 4πε



= 0.529 × 10

−10

m is the ﬁrst Bohr radius and γ =

(1 −v

)

−1/2

is the relativistic factor tabulated in Appendix E; f

(q) is the atomic

scattering factor (or form factor) for an incident x-ray photon and is equal to the

Fourier transform of the electron density within the atom. The atomic number Z in

Eq. (3.2) represents the nuclear charge and denotes the fact that incident electrons

are scattered by the entire electrostatic ﬁeld of an atom, whereas x-rays interact

mainly with the atomic electrons.

3.1.2 Atomic Models

The earliest and simplest model for elastic scattering of charged particles is based

on the unscreened electrostatic ﬁeld of a nucleus and was ﬁrst used by Rutherford

to account for the scattering of α-particles (Geiger and Marsden, 1909). While an

α-particle is repelled by the nucleus, an incident electron is attracted, but in either

case, classical mechanics indicates that the trajectories are hyperbolic (Fig. 3.1).

Both classical and wave-mechanical theory leads to the same expression for the

differential cross section, which is obtained by setting the electronic term f

(q)to

zero in Eq. (3.2), giving

dσ/d = 4γ

(3.3)

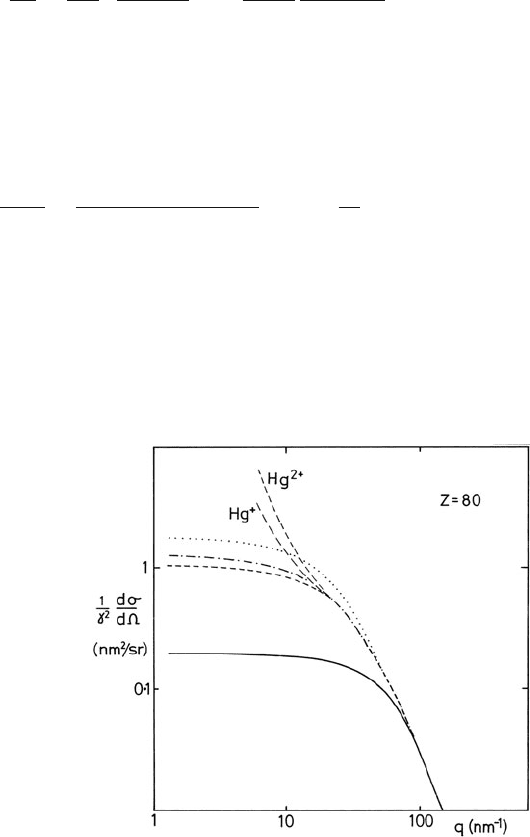
Here q is the magnitude of the scattering vector and is given by q = 2k

sin(θ/2),

as illustrated in Fig. 3.2;  k

= γ m

v is the momentum of the incident electron;

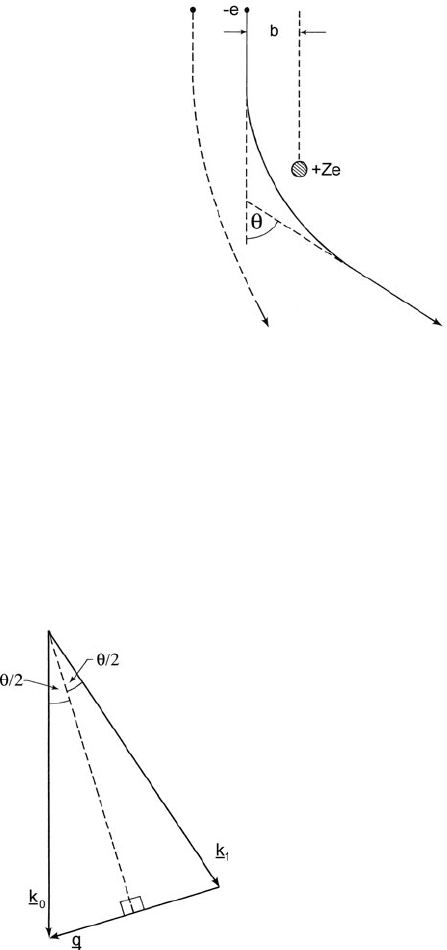
3.1 Elastic Scattering 113

Fig. 3.1 Rutherford

scattering of an electron by

the electrostatic ﬁeld of an

atomic nucleus, viewed from

a classical (particle)

perspective. Each value of

impact parameter b gives rise

to a different scattering angle

θ,andasb increases, θ

decreases because the

electron experiences a weaker

electrostatic attraction. For

small θ, dσ /dΩ is

proportional to θ

–4

and  q is the momentum transferred to the nucleus. For lighter elements, Eq. (3.3)

is a reasonable approximation at large scattering angles (see Fig. 4.24) and is use-

ful for estimating rates of backscattering (θ>π/2) in solids (Reimer, 1989). But

since no allowance has been made for screening of the nuclear ﬁeld by the atomic

electrons, the Rutherford model greatly overestimates the elastic scattering at small

θ (corresponding to larger impact parameter b) and gives an inﬁnite cross section if

integrated over all angles.

Fig. 3.2 Vector diagram for elastic scattering, where k

and k

are the wavevectors of the fast

electron before and after scattering. From geometry of the right-angled triangles, the magnitude of

the scattering vector is q = 2k

sin(θ/2). The direction of q has been chosen to represent momen-

tum transfer to the specimen (opposite to the wavevector change of the fast electron), as normally

required in equations that deal with the effects of elastic and inelastic scattering

114 3 Physics of Electron Scattering

The simplest way of incorporating screening is through a Wentzel (or Yukawa)

formula, in which the nuclear potential is attenuated exponentially as a function of

distance r from the nucleus:

φ(r) = [Ze/(4πε

r)] exp(−r/r

) (3.4)

where r

is a screening radius. Equation (3.4) leads to the angular distribution:

dσ

d

4γ



−2



≈

4γ

(θ

+θ

)

(3.5)

where θ

= (k

)

−1

is a characteristic angle of elastic scattering. The angular

dependence for a mercury atom is shown in Fig. 3.3, and for a carbon atom in

Fig. 3.5. The fraction of elastic scattering that lies within the angular range 0 < θ < β

is (for β  1 rad)

(β)

1 +[2k

sin(β/2)]

−2

≈



1 +



−1

(3.6)

Following Wentzel (1927) and Lenz (1954), an estimate of r

can be obtained

from the Thomas–Fermi statistical model, treating the atom as a free-electron gas,

namely

= a

−1/3

(3.7)

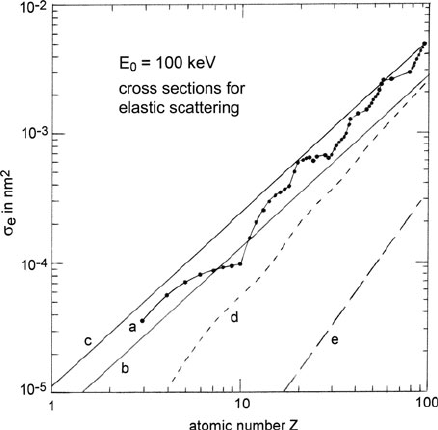
Fig. 3.3 Angular

dependence of the differential

cross section for elastic

scattering of 30-keV electrons

from a mercury atom,

calculated using the Lenz

model with a Wentzel

potential (solid curve) and on

the basis of Hartree–Fock

(dotted curve), Hartree–Slater

(chained curve), and

Dirac–Slater (dashed curve)

wavefunctions. Dirac–Slater

results are also shown for a

single- and double-ionized

atom. From Langmore et al.

(1973), copyright Springer

3.1 Elastic Scattering 115

Integrating Eq. (3.5) over all scattering angles gives



dσ

d

2π sin θ dθ =

4πγ

4/3

= (1.87 ×10

−24

4/3

(v/c)

−2

(3.8)

where v is the velocity of the incident electron and c is the speed of light in vacuum.

For an element of low atomic number, Eq. (3.8) gives cross sections that are accurate

to about 10%, as conﬁrmed by measurement on gases (Geiger, 1964). For a heavy

element such as mercury, the Lenz model underestimates small-angle scattering by

an order of magnitude (see Fig. 3.3), due largely to t he neglect of electron exchange;

for 100-keV electrons Eq. (3.8) gives only about 60% of the value obtained from

more sophisticated calculations (Langmore et al., 1973). Some authors use a coef-

ﬁcient of 0.885 in Eq. (3.7)ortaker

= 0.9a

−1/4

. However, the main virtue of

the Lenz model is that it provides a rapid estimate of the angular dependence of

scattering, as in the L

ENZPLUS program described in Appendix B.

More accurate cross sections are achieved by calculating the atomic potential

from an iterative solution of the Schrödinger equation, as in the Hartree–Fock

and Hartree–Slater methods (Ibers and Vainstein, 1962; Hanson et al., 1964).

Alternatively, electron spin and relativistic effects within the atom can be included

by using the Dirac equation (Cromer and Waber, 1965), leading to the so-called

Mott cross sections. Partial wave methods can be used to avoid the Born approxi-

mation (Rez, 1984), which fails if Z approaches or exceeds 137 (v/c), in other words

for heavy elements or low incident energies.

Langmore et al. (1973) proposed the following equation for estimating the total

elastic cross section of an atom of atomic number Z:

(1.5 ×10

−24

3/2

(v/c)



1 −

596(v/c)



(3.9)

The coefﬁcient and Z-exponent are based on Hartree–Slater calculations; the term

in brackets represents a correction to the Born approximation. The accuracy of

Eq. (3.9) is limited to about 30% because the graph of σ

against Z is in reality

not a smooth curve but displays irregularities that reﬂect the outer-shell structure of

each atom; see Fig. 3.4. A compilation of elastic cross sections (dσ/d and σ

)is

given by Riley et al. (1975), based on relativistic Hartree–Fock wavefunctions.

For an ionized atom, the atomic potential remains partially unscreened at large r,

so dσ/d continues to increase with increasing impact parameter (decreasing θ );

see Fig. 3.3. As a result, the amount of elastic scattering can appreciably exceed that

from a neutral atom, particularly in the range of low scattering angles (Anstis et al.,

1973; Fujiyoshi et al., 1982).

The scattering theory just described is based on the properties of a single isolated

atom. In a molecule, the cross section per atom is reduced at low scattering angles,

116 3 Physics of Electron Scattering

Fig. 3.4 Cross section σ

for elastic scattering of 100-keV electrons, calculated by Humphreys

et al. (1974). Curve a shows individual data points derived from Doyle–Turner scattering factors,

based on Hartree–Fock wavefunctions. Lines b and c represent the Lenz model, with and without

a multiplying factor of 1.8 applied to Eq. (3.8). Curves d and e give cross sections [σ

− σ

(β)]

for elastic scattering above an angle β of 24 and 150 mrad, respectively. Note that the atomic-shell

periodicity in the Z-dependence disappears as β becomes large and the scattering approximates

to Rutherford collision with small impact parameter, where screening by outer-shell electrons is

unimportant

typically by 10–20%, as a result of chemical bonding (Fink and Kessler, 1967). In

a crystalline solid, the angular dependence of elastic scattering is changed dramat-

ically by diffraction effects but in an amorphous solid, diffraction i s weak and an

atomic model can be used as a guide to the magnitude and angular distribution of

elastic scattering. As an alternative to describing the amount of scattering in terms of

a cross section (σ

per atom), one can use an inverse measure: λ

= (σ

)

−1

, where

is the number of atoms per unit volume of the specimen. In an amorphous mate-

rial at least, the mean free path λ

can be thought of as the mean distance between

elastic collisions.

3.1.3 Diffraction Effects

In a crystalline material, the regularity of the atomic arrangement requires that the

phase difference between waves scattered from each atom be taken into account by

introducing a structure factor F(θ) deﬁned by

3.1 Elastic Scattering 117

F(θ) =



(θ)exp(−iq ·r

) (3.10)

Here, r

and f

are the coordinate and scattering amplitude of atom j, with q·r

the

associated phase factor; the sum is carried out over all atoms (j = 1, 2, etc.) in the

unit cell. Equation (3.10) can also be expressed in the form

F(θ) ∝



V(r)exp(− q ·r) dτ (3.11)

where V(r) is the scattering potential and the integration is carried out over all vol-

ume elements within the unit cell. Equation (3.11) indicates that the structure factor

is related to the Fourier transform of the lattice potential.

The intensity scattered in a direction θ relative to the incident beam is |F(θ)|

and peaks at values of θ for which the scattered waves are in phase with one

another. Each diffraction maximum (Bragg beam) can also be regarded as repre-

senting “reﬂection” from atomic planes, whose spacing d depends on the Miller

indices and unit-cell dimensions. Bragg reﬂection occurs when the angle between

the incident beam and the diffracting planes coincides with a Bragg angle θ

deﬁned by

λ = 2d sin θ

(3.12)

where λ = 2π/k

is the incident electron wavelength. The scattering angle θ is

twice that of θ

,soEq.(3.12) is equivalent (for small θ

, large v)toλ = θd.For

100-keV incident electrons, λ = 3.7 pm and the scattering angles corresponding to

Bragg reﬂection exceed 10 mrad in simple materials. Larger values of θ

correspond

to reﬂection from planes of smaller separation or to higher order reﬂections whose

phase difference is a multiple of 2π.

The Bragg-reﬂected beams can be recorded by a two-dimensional detector such

as a CCD array. For a single-crystal specimen, the diffraction pattern consists of an

array of sharp spots whose symmetry and spacing are closely related to the crys-

tal symmetry and lattice constants. In the case of a polycrystalline sample whose

crystallite size is much less than the incident beam diameter, random rotational aver-

aging produces a diffraction pattern consisting of a series of concentric rings, rather

than a spot pattern.

The relative intensities of the lowest order Bragg beams (for the case of a thin

diamond specimen) are shown in Fig. 3.5 and are seen to follow the overall trend

predicted by a single-atom model. Distributions of inelastic scattering from the inner

(K-shell) and outer-shell (valence) electrons are also shown and are seen to be much

narrower in angular range. In fact, each Bragg beam generates inelastic scattering

within the specimen, so each Bragg spot in a diffraction pattern is surrounded by

a halo of inelastic scattering. This inelastic scattering can be removed by zero-loss

ﬁltering of the diffraction pattern, which sharpens the Bragg spots and reduces the

background between them.