Душков Б.А., Королев А.В., Смирнов Б.А. Психология труда, профессиональной, информационной и организационной деятельности

Подождите немного. Документ загружается.

Первоначально К. рассматривалась как функция интел-

лекта, и уровень развития интеллекта отождествлялся с уров-

нем развития К. Впоследствии выяснилось, что уровень

интеллекта коррелирует с К. лишь до определенного преде-

ла, а слишком высокий интеллект препятствует К. В насто-

ящее время К. рассматривается как несводимая к интеллек-

ту функция целостной личности, зависящая от целого ком-

плекса ее психологических характеристик. Соответственно,

центральное направление в изучении К.— выявление лично-

стных качеств, с которыми она связана.

К. является профессионально важным качеством для опе-

раторов-руководителей, операторов-исследователей (см.

Типы операторской деятельности). Для диагностики К.

могут использоваться батареи тестов Гилфорда (10 тестов

на вербальную К. и 4 — на невербальную) и Торранса. В со-

став батареи Торранса входит 12 тестов, диагностирующих

три сферы творчества: словесное творческое мышление,

изобразительное творческое мышление и словесно-звуко-

вое творческое мышление. Для оценки уровня К. при ис-

пользовании данной батареи используются три показателя:

1) легкость — быстрота выполнения задания; 2) гибкость —

число переключений с одного класса объектов на другой в

ходеопытов; 3) оригинальность, оцениваемая минимальной

частотой данного ответа среди ответов однородной группы

испытуемых.

КРЕСЛО ОПЕРАТОРА — элемент рабочего места, предназ-

наченный для поддержания человеком рабочей позы в по-

ложении «сидя». Обязательными элементами К. о. являются

сиденье, спинка и подлокотники. Дополнительными элемен-

тами могут быть подголовники, средства перемещения сиде-

нья в горизонтальной плоскости, а также вокруг оси, под-

ставки для ног, используемые при выполнении всех видов

работ, связанных с длительным сохранением положения

сидя.

. К К. о., предназначенным для использования в течение

длительного времени, независимо от их профессионального

назначения предъявляются следующие требования: обеспе-

чение поддержания правильной и удобной рабочей позы;

создание условий для изменения рабочей позы; обеспече-

ние нормальной деятельности сердечно-сосудистой, дыха-

тельной и пищеварительной систем; конструкция К. о. не

должна вызывать болезненных ощущений, возникающих в

результате давления элементов сиденья на тело человека;

учет антропометрических характеристик при выборе

формы и глубины сиденья. К. о. должно также обеспечи-

вать удобную рабочую позу, надежную опору для тела с 261

262

учетом выполняемых оператором действий, а при необхо-

димости и удобную позу при отдыхе. Для свободного вста-

вания предусматривается возможность перемещения сиде-

нья вместе с подлокотниками и спинкой по отношению к

его основанию вперед — назад на 180 — 200 мм и поворот вок-

руг оси не менее ±90° от исходного положения. К. о. долж-

но способствовать ослаблению, вибрационных и ударных

воздействий, если они специфичны для данного вида дея-

тельности.

КРИВАЯ УПРАЖНЕНИЯ (обучения) — графическая зави-

симость успешности выполняемого действия от типа и чис-

ла тренировочных упражнений. К. у. в форме графика вы-

ражает последовательное уменьшение числа ошибок или

времени выполнения действия в зависимости от времени

тренировки (числа упражнений). Особенности К. у. опреде-

ляются психологическими закономерностями процесса

формирования навыка, в т. ч. типом (степенью сложности)

усваиваемого действия и используемыми в обучении спосо-

бами тренировки. Наиболее трудным, требующим объясне-

ния, является вопрос о психологическом механизме после-

довательного исключения ошибок в процессе тренировки.

Одна из наиболее распространенных гипотез основывается

на теоретическом представлении о механизме обратной

связи (подкреплении) как основном психологическом регу-

ляторе, обеспечивающем при каждом последующем выпол-

нении упражнения коррекции и последовательное закреп-

ление требуемого правильного действия.

К. у. различны для разных типов действий. В процессе

формирования сложных типов действий на К. у. наблюда-

ются такие периоды, когда в процессе последующего уп-

ражнения число ошибок и время выполнения работы не

уменьшаются. Такие периоды называются плато и, очевид-

но, представляют специальные периоды перехода от одного

типа психической регуляции действия к существенно новым

типам регуляции. Прогнозирование периодов задержки в

процессе формирования действия имеет существенное зна-

чение при необходимости достижения высоких уровней ма-

стерства, а также при разработке специальных программ

для тренажеров (в авиации, космонавтике, энергетике, АСУ

и т. д.). Те или иные действия — практические, интеллекту-

альные, речевые и пр.— характеризуются различными оп-

тимальными условиями и выражаются в К. у. разнообраз-

ных типов.

Для многих типов операторской деятельности, особен-

но в тех случаях, когда она носит алгоритмический харак-

тер, выполняется строго по инструкции, К. у. носит плав-

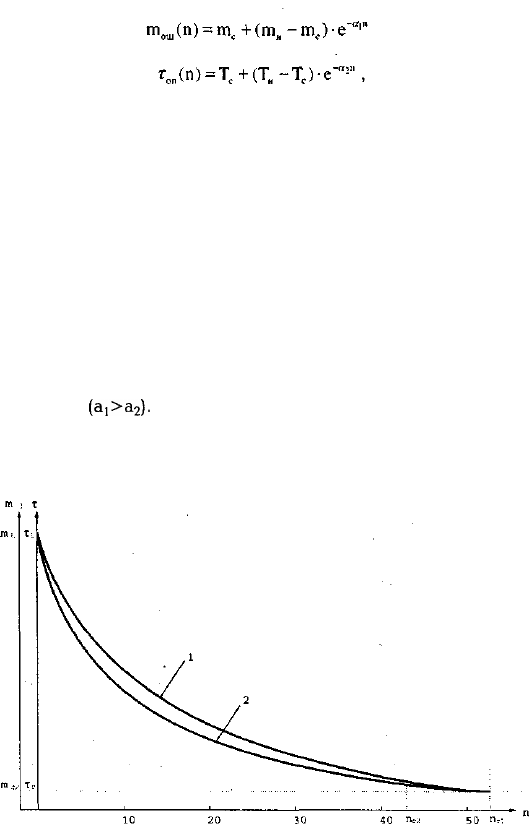
ный характер и описывается чаще всего экспоненциальной

функцией:

где т

ош

(п) и т

оп

(п) — соответственно число ошибок и время

решения задачи оператором, ш

и Т

— стационарные зна-

чения этих показателей, т

и Т

— их исходные значения,

п — число тренировок (упражнений), aj и а

— показатели

скорости обучения по безошибочности и скорости выпол-

нения работы.

Из приведенных графиков (см. рис. 7) и формул следу-

ет, что основными критериями для выхода оператора на ста-

ционарный уровень обученности являются, во-первых, мак-

симально возможные для данных условий результаты дея-

тельности (минимум числа ошибок и времени выполнения

задания) и, во-вторых, относительная стабильность этих

результатов во времени. При этом нужно иметь в виду, что

обычно выход на стационарный уровень обученности по

быстродействию осуществляется быстрее, чем по безоши-

бочности

(ai>a

Поэтому число упражнений для выхода на

стационарный уровень по безошибочности, как правило,

больше, чем по скорости, т. е. п

с1

>п

с2

. Учитывая это усло-

вие, можно определить продолжительность обучения:

Рис. 7. Кривые обучения: 1 —по безошибочности,

2 — по своевременности выполнения работы 263

264

где T] — периодичность (продолжительность) проведения

отдельных циклов упражнений.

Приведенные на рис. 7 кривые отражают лишь общую

тенденцию изменения навыков в процессе обучения, усред-

ненную по достаточно большому числу операторов. Реаль-

но же индивидуальные К. у. носят, как правило, немонотон-

ный характер; они имеют промежуточные плато и подъемы,

что обусловливается переходом в процессе обучения к

новым стратегиям по мере усвоения приобретенных навы-

ков (см. Трансформационная теория обучения).

КРИТЕРИАЛЬНОЕ ЗАДАНИЕ (от лат. kriterion — мерило,

средство суждения...) — материал, предъявляемый испытуе-

мым с целью психодиагностики их умственного развития или

уровня профессиональной подготовленности. Важность раз-

работки и практического использования К. з. особенно воз-

росли в последнее время в связи с появлением в психодиаг-

ностике нового направления — критериально-ориентирован-

ного тестирования (КОРТ). Определение задания в качестве

критериального обусловлено двумя факторами. Первый зак-

лючается в том, что предъявленный в К. з. материал позволя-

ет дать репрезентативную и обобщенную совокупность зна-

ний и умений, относящихся к внутренней завершенной обла-

сти учебной и профессиональной деятельности. Второй

фактор определяет возможность весьма близкого к содержа-

нию задания психологического декодирования. Область при-

менения КОРТ ограничена рамками диагностики достижений

в учебной и профессиональной деятельности.

Критериально-ориентированные тесты являются разновид-

ностью тестов достижений (см. тест). Эти тесты ориентируют-

ся преимущественно на концепцию критерия как определен-

ного круга знаний, навыков, специфических операций, остав-

ляя без внимания зачастую их психологическое содержание.

Если в традиционных психологических тестах оценка резуль-

татов испытуемого определяется на основе статистической

нормы, в результате чего говорят о порядковом номере чело-

века в группе, то в КОРТах эта оценка свидетельствует о бли-

зости результатов испытуемого к внешнему нормативу, т. е.

К. з. Норматив берется из содержания деятельности и соответ-

ствует минимально необходимому или идеальному профилю

достижений. Уровень выполнения К. з. зависит как от специ-

альных знаний, так и от общего интеллекта испытуемого.

КРИТЕРИИ СОГЛАСИЯ — статистические критерии, исполь-

зуемые для оценки степени совпадения двух или нескольких

статистических совокупностей (выборок). К. с. могут быть

непараметрическими и параметрическими. В первом случае

используются не сами значения наблюдаемых величин, а толь-

ко их упорядоченность (для каждой пары величин известно,

какая из них больше), т. е. критерии, не зависящие от парамет-

ров распределений. Такие критерии весьма удобны для прак-

тического использования, т. к. требуют меньшего объема вы-

числений и априорных сведений и могут использоваться даже

при невозможности прямых измерений изучаемых признаков.

Основными из непараметрических К. с. являются критерий

знаков, критерий Смирнова и критерий Вилконсона. Крите-

рий знаков используется для обнаружения достаточно грубых

различий совокупностей. Пусть имеются две выборки Xi....x

У1-—У2- Вычисляются величины Zj = Xj — у\, (i = 1,N) и про-

веряется гипотеза о том, что P(Z

> 0) = 0,5. Если гипотеза

выполняется (т. е. числа положительных Z, > 0 и отрицатель-

ных

Zj<0

значений несущественно отличаются друг от друга),

то между выборками х и у нет существенных различий. Кри-

терий Смирнова позволяет непараметрически проверить со-

впадение друг с другом статистических распределений. Крите-

рий Вилконсона также применяется для проверки гипотезы о

совпадении выборок. Две выборки Xj...x

и У;...у

вместе ран-

жируют в порядке возрастания и в едином ряду подсчитыва-

ется число инверсий (число x

появившихся после yj). Если это

число близко к 0,5п, то различие между выборками можно

считать несущественным.

При использовании параметрических критериев вычис-

ляются значения параметров сравниваемых распределений.

Это усложняет применение критериев, однако позволяет по-

лучить более точные результаты. Основными из параметри-

ческих критериев являются критерий Фишера, критерий

Стьюдента и критерий с

. Критерий Фишера используется

для проверки статистических гипотез о равенстве диспер-

сий двух или нескольких совокупностей. Критерий приме-

няется в тех прикладных задачах, где необходимо исследо-

вать стабильность изучаемых величин. Напр., он может быть

применен для сравнения рассеяний ошибок двух операто-

ров, разбросов оценок экспертов, полученных по разным

методикам, проверки однородности латентных периодов

реакций в различных экспериментах и т. д. Применение

этого и других К. с. возможно, если сравниваемые выборки

подчинены нормальному закону распределения.

Различие между двумя дисперсиями of и о; является зна-

чимым, если выполняется условие:

265

где

p—

значение случайной переменной, подчиненной

распределению Фишера

— 1 и

— 1 степе-

нями свободы; Р — уровень значимости;

— объемы

выборок. Значения

Р^.рнаходятся

из статистических таблиц

для данных значений

При пользовании таблицами

и формулой следует иметь в виду, что индекс 1 всегда от-

носится к большой дисперсии, а индекс 2 — к меньшей.

Критерий Стьюдента применяется для проверки значимос-

ти различия между двумя средними значениями

Это

различие значимо, если выполняется условие:

ния континуума наблюдения на два класса, соответствую-

щих разным ответным реакциям. Но если порог рассматри-

вается как нижний предел чувствительности сенсорной

системы, то понятие К. п. р. отражает участие в работе

системы различных внесенсорных факторов, таких как мо-

тивы, установки, тенденции к угадыванию и т. п. При одном

и том же уровне чувствительности испытуемый может уста-

новить для себя совершенно различный К. п. р., что будет не-

посредственно сказываться на показываемых им результа-

тах, меняя уровень обнаружения и ложной тревоги.

КРИТИЧЕСКАЯ ЧАСТОТА МЕЛЬКАНИЙ (КЧМ) — мини-

мальная частота проблесков, при которой возникает их

слитное восприятие. Эта частота зависит от яркости про-

блесков В и подчиняется основному психофизическому

закону (закон Фехнера):

где а — константа, зависящая от размеров и конфигурации

законов, а также от спектрального состава мелькающего

изображения. При обычных условиях наблюдения f

= 20 —

25 Гц, при зрительном утомлении эта частота понижается.

На величину f

оказывает действие также продолжитель-

ность проблесков, т. е. соотношение длительностей светлой

(проблеск) и темной (отсутствие проблеска) фаз. Для учета

этого фактора воспринимается яркость В, которая рассчи-

тывается по формуле:

где В

об

— объективная яркость, q — скважность проблес-

ков (отношение длительности светлой фазы к периоду про-

блесков). КЧМ зависит также от размеров экрана (изобра-

жения): чем больше эти размеры, тем выше f

. Поэтому

частота смены кадров на киноэкранах, проекционных, эк-

ранах коллективного пользования обычно больше, чем ча-

стота кадров в телевидении. В общем же случае вопрос о

частоте мельканий имеет большое значение при решении

двух видов практических задач. В тех случаях, когда необ-

ходимо, чтобы мелькания не замечались (напр., при проек-

тировании изображения на экран, в технике кино и телеви-

дения), частота смены информации должна превышыше f

.и

составлять не менее 40 Гц. При необходимости использовать

мелькание для кодирования следует иметь в виду, что наи-

меньшее зрительное утомление будет при частоте 3 — 8 Гц. 267

268

КУЛЬТУРА ПРОИЗВОДСТВА — комплексное понятие, вклю-

чающее технико-организационную культуру предприятия,

культуру труда и личную культуру работающих. Технико-

организационная культура предприятия охватывает техни-

ку, технологию, организацию производства и управления.

Культура труда включает организацию и обслуживание

рабочих мест, механизацию и автоматизацию труда, каче-

ство и внешний вид выпускаемой продукции; соответствие

производственного оборудования анатомическим, физиоло-

гическим и психологическим требованиям, санитарно-гигие-

нические условия труда и культурно-бытовое обслуживание

работников на производстве. Личная культура работающих

определяется их общим культурным и профессиональным

уровнем, компетентностью, отношением к выполняемой

работе, манерами поведения.

«КУРС ИНЖЕНЕРНОЙ ПСИХОЛОГИИ» — учебник по ин-

женерной психологии для студентов университетов, обу-

чающихся по специальности психология (Котик М. А.

Курс инженерной психологии.— Таллин: Валгус, 1978.—

364 с, ил.).

Учебник создан на базе двух ранее изданных учебных

пособий, в основу которых был положен курс инженер-

ной психологии, читаемый в течение длительного времени

автором. Включает четыре раздела. В первом из них рас-

сматриваются общие закономерности деятельности чело-

века в системе управления. Рассмотрены история инженер-

ной психологии и ее связь с другими науками, дана харак-

теристика человека как компонента системы управления,

приведена общая психологическая характеристика деятель-

ности оператора и дан ее подробный информационный

анализ. Второй раздел посвящен анализу и определению

показателей работы оператора и СЧМ. Проанализированы

показатели точности, надежности и времени работы опе-

ратора, показано их влияние на аналогичные характерис-

тики СЧМ. В третьем разделе описаны технические сред-

ства деятельности оператора. Подробно рассмотрены на-

значение, классификация, инженерно-психологические

характеристики различного рода средств отображения

информации и органов управления; приведены принципы

их согласования между собой и с особенностями деятель-

ности оператора. В четвертом разделе представлены мето-

ды отображения и описания деятельности оператора и

рассмотрены основные принципы и подходы к проектиро-

ванию СЧМ.

При изложении материала автор исходит из такой точ-

ки зрения: для инженерной психологии наиболее существен-

но выявление основных психических закономерностей де-

ятельности оператора, формализация же их является вто-

ричной задачей, при решении которой в помощь психологу

могут привлекаться инженеры и математики. Поэтому при

изложении материала основное внимание уделяется общим

принципам, теоретическим подходам к выявлению искомых

закономерностей, их обоснованию, а не описанию частных

алгоритмов деятельности оператора.

269

270

ЛАБИЛЬНОСТЬ (от лат. labilis — скользящий, неустойчи-

вый) — одно из свойств нервной системы, характеризую-

щее скорость возникновения и прекращения нервных про-

цессов. Л. проявляется в способности нервных клеток пере-

ходить из возбужденного состояния в тормозное и наоборот.

С физиологической точки зрения Л. представляет максималь-

ное число волн возбуждения, которые данная ткань или

нервная клетка способны воспринимать в единицу времени

в точном соответствии с ритмом стимуляции. Л. может

изменяться как при прямых (физических или химических)

воздействиях на возбудимую ткань, так и под влиянием

приходящих к ней импульсов. Кроме того, под Л. часто

понимают неустойчивое психическое и физиологическое

состояние человека.

ЛАБОРАТОРНЫЙ ЭКСПЕРИМЕНТ (от лат. laborare — ра-

ботать, experimentum — опыт) — разновидность эксперимен-

та, проводимого в условиях специально оборудованных

помещений, что обеспечивает особенно строгий контроль

независимых и зависимых переменных. Л. э. представляет

собой одну из разновидностей моделирования деятельности

человека (физическое моделирование). Смысл его заключа-

ется в том, что перед испытуемым ставится задача: в лабо-

раторных условиях выполнить определенные действия, по

психологической структуре наиболее точно соответствую-

щие реальной деятельности. Такое моделирование позволя-

ет в лабораторных условиях изучить какую-либо реальную

деятельность с большой точностью регистрации и замеров.

Однако в силу искусственности лабораторных условий

полученные результаты могут отличаться от тех, которые

имеют место в реальной деятельности человека. Поэтому

Л. э. (так же как и другие виды моделирования) имеет лишь

определенное приближение к реальной деятельности. Его