Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

644 20 Fluid Flows with Heat Transfer

Temperature distribution

Velocity distribution

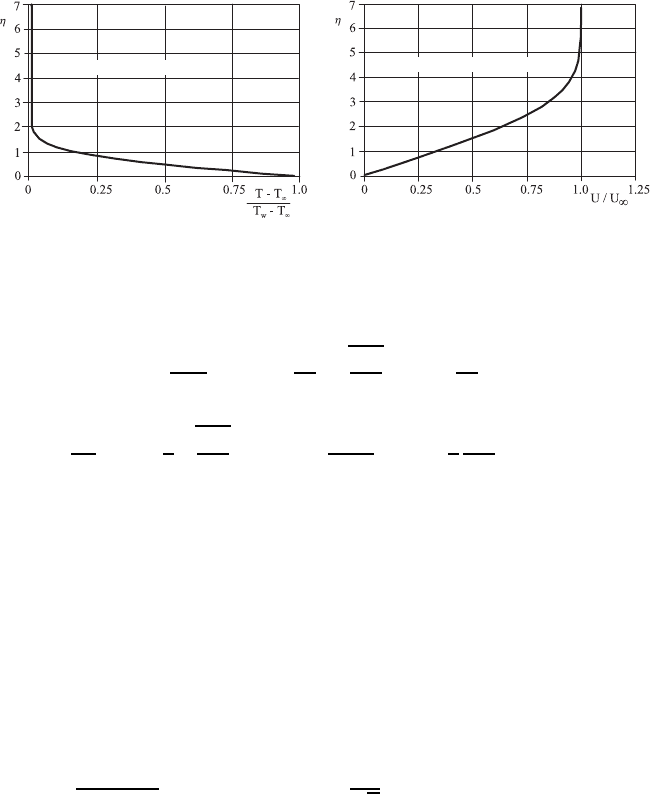
Fig. 20.10 Temperature distribution and velocity distribution for a plate boundary-

layer ﬂow with constant wall temperature at small Prandtl numbers

one obtains for the derivative in the above diﬀerential equation (20.89)

∂T

∗

∂x

= f



−

∞

= ηf



, (20.91)

∗

= f



∞

and

∂

∗

∂y

= f





∞



. (20.92)

From (20.91) and (20.92), the following ordinary diﬀerential equation for

f(η)canbederived:



+2ηf



=0. (20.93)

With the following boundary conditions:

For all x ≥ 0:

∗

(y =0)=1 ; η =0: f (η)=1,

∗

(y →∞)=0 ; η =1: f (η)=0

one obtains for the temperature distribution



T − T

∞

− T

∞



=1− erf(η)=1−

√

exp

−η

dη. (20.94)

This temperature distribution is given as function of η in Fig. 20.10 together

with the corresponding temperature distribution. For more details, see ref.

[20.5]

20.6 Similarity Solution for a Plate Boundary Layer

with Wall Heating and Dissipative Warming

In Chap. 15, boundary-layer ﬂows were discussed and an introduction was

given to the solution of the boundary-layer equations by means of similarity

ansatzes. The ﬂat plate ﬂow with heat transfer discussed here, is likewise

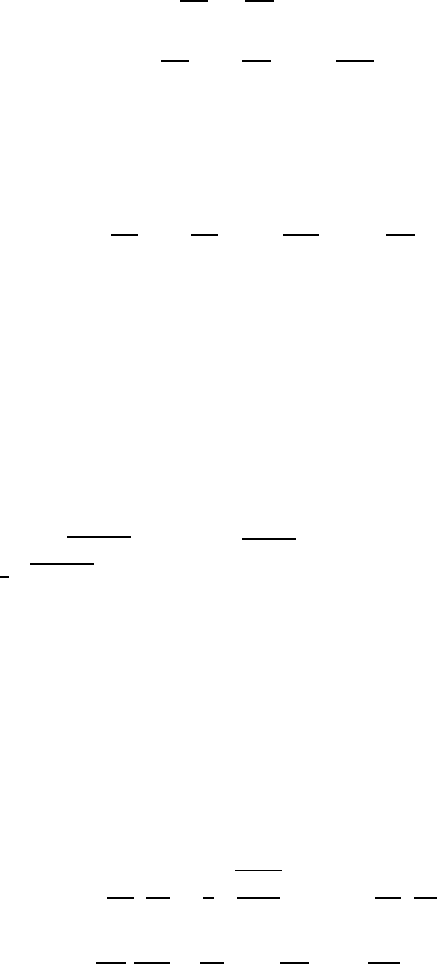
20.6 Similarity Solution for a Plate Boundary Layer 645

based on the solution of the boundary-layer equations for the stationary

ﬂow around plates suggested by Blasius, i.e. on the solution of the following

equations:

∂U

∂x

∂V

∂y

=0, (20.95)



∂U

∂x

+ V

∂U

∂y



= µ

∂

∂y

. (20.96)

For the discussion of the heat transfer, the boundary-layer form of the energy

equation is included. For the solution to be sought, the temperature depen-

dences of the material values ρ, µ, λ, and thus also the buoyancy forces, are

neglected in the energy equation:

ρc



∂T

∂x

+ V

∂T

∂y



= λ

∂

∂y

+ µ



∂U

∂y



. (20.97)

For ﬂat plate ﬂow with wall heating, the following boundary conditions result:

y =0:U = V =0 and T = T

, (20.98)

y =0:U → U

∞

and T → T

∞

. (20.99)

For the solution of the ﬂat plate boundary layer problem, it is important to

realize that (20.95) and (20.96), for the determination of the velocity ﬁeld,

are decoupled from the energy equation (20.97) if the material properties

are assumed to be independent of the temperature. This assumption is made

here. Thus, for the velocity ﬁeld the solution suggested by Blasius can be

taken (see Chap. 16).

With η = y



∞

/νx and ψ =

√

νxU

∞

f(η), one obtains U = U

∞



(η)

and V =



νU

∞

/x − (ηf



− f ).

From the momentum equation, the following diﬀerential equation for the

quantity f can be derived:



+2f



=0. (20.100)

AsshowninChap.16,f(η)andf



(η) can be determined numerically from

this, and thus U and V can be determined for the boundary conditions

reading as follows:

η =0: f = f



=0 and η →∞: f



→ 1.

The energy equation can be treated as follows:

∞



dη

∂η

∂x

νU

∞

(ηf



− f )

dη

∂η

∂y

ρc

∂

∂η



∂η

∂y



ρc



∞

νx

(20.101)

646 20 Fluid Flows with Heat Transfer

or rewritten for further considerations:

−



dη



µc



1/P r

dη

∞



)

(20.102)

in order to obtain the ﬁnal form:

dη

+2Pr

∞



)

. (20.103)

On now introducing

Θ (η)=

T − T

∞

− T

∞

(20.104)

one obtains the following ordinary diﬀerential equation of Θ:

0=Θ



fΘ



+2Pr

∞



)

. (20.105)

Without dissipative heating of the boundary layer, given by the last term in

(20.105), one obtains the diﬀerential equation



fΘ



= 0 (20.106)

which has to be solved for the boundary conditions:

η =0; θ =1 and η →∞; θ → 0.

A solution of this equation is possible, as f(η)isknown.Itwasderivedas

a solution of the continuity and momentum equations. It was suggested by

Pohlhansen [20.3] and is given in Fig. 20.11 for diﬀerent Prandtl numbers:

Fig. 20.11 Temperature distribution at a plane heated plate with temperature

diﬀerence (T

− T

∞

)

20.7 Vertical Plate Boundary-Layer Flows 647

For heat-transfer computations, the following equations hold:

˙q (x)=−λ



∂T

∂y



= −λ



∂T

∂η





∂η

∂y



, (20.107)

˙q (x)=−λ



∂Θ

∂η



− T

∞

)

∞

νx

. (20.108)

For the technically interesting ﬁelds the following holds:



∂Θ

∂η



≈

(Pr)

1/3

(20.109)

so that for the local heat ﬂow we obtain

˙q (x)=−

λP r

1/3

− T

∞

)

∞

νx

. (20.110)

The amount of heat which is released from the tip of the plate up to the

plate-length L can be obtained by integration:

Q (L)=+

λP r

1/3

− T

∞

)

∞

−3/2

. (20.111)

In this way, important information for technical engineering can be gained

from the above derivations.

20.7 Vertical Plate Boundary-Layer Flows Caused

by Natural Convection

Near a vertical plane, which was heated up to temperature T

,anatural

convection boundary-layer ﬂow develops, which is caused by natural convec-

tion and is directed upwards. It is described by the boundary-layer equations

by dP/∂x =0:

∂U

∂x

∂V

∂y

=0, (20.112)



∂U

∂x

+ V

∂U

∂y



= µ

∂

∂y

+ ρgβ (T − T

∞

) , (20.113)

ρc



∂T

∂x

+ V

∂T

∂y



= λ

∂

∂y

. (20.114)

For β =

∞

and θ =

T −T

∞

−T

∞

, these equations can be transcribed as follows

and can be employed for the solution of the velocity and temperature ﬁelds:

648 20 Fluid Flows with Heat Transfer

∂U

∂x

∂V

∂y

=0, (20.115)



∂U

∂x

+ V

∂U

∂y



= µ

∂

∂y

+ ρg

− T

∞

Θ, (20.116)

∂Θ

∂x

+ V

∂Θ

∂y

= a

∂

∂y

. (20.117)

The introduction of the stream function U =

∂ψ

∂y

and V = −

∂ψ

∂x

eliminates

the continuity equation and makes possible the similarity ansatz given below:

Ψ =4νAx

3/4

f (η)withη = A

√

(20.118)

with A being

A =

g (T

− T

∞

)

4ν

∞

. (20.119)

The velocity components U and V can be computed as follows:

U =4νx

1/2



and V = νAx

−1/4

(ηf



− 3f)

and the derivatives yield:

∂U

∂x

νA

√

(2f



− ηf



) ,

∂V

∂y

νA

√

(ηf



− 2f



) .

With this results the following set of diﬀerential equations, which can be

employed to determine the similarity functions f(η)andθ(η):



+3ff



− 2f



+ Θ =0 and Θ



+3PrfΘ



=0, (20.120)

where the following boundary conditions determine the problem:

η =0: f = f



=0 and Θ =1, (20.121)

η →∞: f



=0 and Θ =0. (20.122)

The numerical integration of the diﬀerential equation system was carried out

by Pohlhansen [20.3] and Ostrach [20.2] and led to the solutions stated in

Fig. 20.12 for diﬀerent Prandtl numbers.

On computing now the heat ﬂow existing locally per unit time and unit

area, one obtains:

˙q (x)=−λ



∂T

∂y



= −λ



∂Θ

∂η





∂η

∂y



− T

∞

) (20.123)

20.8 Similarity Considerations for Flows with Heat Transfer 649

Fig. 20.12 Temperature and velocity distribution at a heated vertical plane plate

caused by natural convection

or, after carrying out the diﬀerentiation



∂η

∂y



,oneobtains:

˙q (x)=−λA

√

− T

∞

)



∂Θ

∂η



. (20.124)

For Pr = 0.73 one obtains (

∂θ

∂η

)

≈

, so that the following expression holds

for ˙q(x):

˙q (x) ≈−

λA

√

− T

∞

) . (20.125)

Integration over the plate length L results in the heat transfer per unit

width:

Q =

3/4

λA (T

− T

∞

) . (20.126)

On computing the Nusselt number, averaged over L,oneobtains

Q =

λ (Nu)

− T

∞

(Nu)

=0.667AL

3/4

(20.127)

a relationship which is well conﬁrmed by experimental results.

20.8 Similarity Considerations for Flows

with Heat Transfer

In Chap. 6, general considerations on the similarity of ﬂuid ﬂows were carried

out. They can be extended to ﬂows with heat transfer as shown below.

The momentum equations of ﬂuid mechanics can be written as follows:



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

−

∂τ

∂x

+ ρg

. (20.128)

650 20 Fluid Flows with Heat Transfer

As far as Newtonian ﬂuids are concerned, for the molecular-dependent

momentum transport one can write

= −µ



∂U

∂x

∂U

∂x



µδ

∂U

∂x

. (20.129)

In order to write (20.128) in dimensionless form, the molecular-dependent

momentum transport to the wall, τ

, is introduced. All other quantities

are made dimensionless with characteristic quantities of the ﬂow and heat-

transfer system. Therefore, the following quantities can be introduced:

ρ = ρ

∗

; U

= U

∗

; t = t

∗

; x

= l

∗

; P = ∆P

∗

; τ

= τ

∗

and g

= 0, so that one obtains the following equation:

∗

∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗

= −

∆P

∂P

∗

∂x

∗

−

∂τ

∗

∂x

∗

. (20.130)

On introducing U

= τ

/ρ = u

and ∆P

= τ

, the right-hand side of the

equation reduces to a dimensionless form, where the quantities are written

with an asterisk. The dimensionless groups of variables before the asterisked

quantities are now all made equal to 1.

On applying the dimensionless quantities stated in (20.130) also to

(20.129), one obtains

∗

= −

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

. (20.131)

This equation becomes dimensionless on introducing as characteristic length

= ν

On introducing all these characteristic quantities into (20.128) and

(20.129) to make them also dimensionless, one obtains the following forms of

these two equations:

∗



∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗



= −

∂P

∗

∂x

∗

−

∗

(20.132)

and

∗

= −µ

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

. (20.133)

For similarity considerations, the following quantities were introduced as

dimensionless velocity, dimensionless pressure diﬀerence and dimensionless

length and time scales:

= u



/ρ; ∆P

= τ

; l

= ν

; t

= ν

. (20.134)

References 651

On extending the above-mentioned dimensionless considerations to the

general form of the energy equation:

ρc



∂T

∂t

+ U

∂T

∂x



= −

∂q

∂x



∂P

∂t

+ U

∂P

∂x



− τ

∂U

∂x

(20.135)

and the Fourier law for heat conductivity:

˙q

= −λ

∂T

∂x

(20.136)

the dimensionless form of the energy equation can be derived as follows:

∗



∂T

∗

∂t

∗

+ U

∗

∂T

∗

∂x

∗



= −

˙q

P,c

∆T

∂ ˙q

∗

∂x

∗

−

∆P

P,c

∆T





∂P

∗

∂t

∗

+ U

∗

∂P

∗

∂x

∗



−

P,c

∆T

∗

∂U

∗

∂x

∗

. (20.137)

Looking at (20.137), one sees that the following quantities have to be in-

troduced as characteristic quantities, in order to conserve the dimensionless

form of the energy equation equivalent to (20.132):

∆T

P,c

and ˙q

= τ

. (20.138)

Standardization of the Fourier law leads to the following result:

˙q

∗

= −

∆T

∗

∂T

∗

∂x

∗

→ l



∆T

˙q

P,c





(20.139)

where Prl

= l

and Prt

= t

can be stated. This represents the connection

between the characteristic length and time scales for the heat and momentum

transport.

References

20.1. Illingworth, C. R.: Some solutions of the equations of ﬂow of a viscous

compressible ﬂuid, Proc. Cambridge Phil. Soc., 46, pp. 469–478, 1950

20.2. Ostrach, S.: An analysis of laminar free-convection ﬂow and heat transfer about

a ﬂat plate parallel to ghe direction of the generating bridge force, NACA-

Report 1111, 1953

20.3. Pohlhansen, E.: Der W¨armeaustausch zwischen festen K¨orpern und

Fl¨ussigkeiten mit kleiner Reibung und kleiner W¨armeleitung, ZAMM 1, pp.

115–121, 1921

20.4. M¨uller, U. and Ehrhard, P.: Freie Konvektion und W¨arme¨ubertragung, C. F.

M¨uller, Springer, Berlin Heidelberg New York, 1999

20.5. Schlichting, H.: Boundary Layer Theory, McGraw-Hill, New York, 1979

Chapter 21

Introduction to Fluid-Flow Measurement

21.1 Introductory Considerations

The derivation of the Reynolds equations, as a basis for numerical ﬂow in-

vestigations, led to a system of diﬀerential equations which, in addition to

the mean values of the components of the ﬂow velocity and the static pres-

sure, contain also turbulent transport terms. These terms represent, for the

turbulent momentum transport, time mean values of the products of veloc-

ity ﬂuctuations. These transport terms were derived from the Navier–Stokes

equations by introducing into the equation mean velocity components and

turbulent velocity ﬂuctuation, and by averaging them afterwards with re-

spect to time. Although the turbulent transport terms were derived formally,

as new unknowns of the ﬂow ﬁeld, physical importance can be attached to

them. They represent, in the averaged momentum equations, additional dif-

fusive momentum-transport terms, which occur in ﬂows due to turbulent

velocity ﬂuctuations that occur superimposed on the mean velocity ﬁeld.

When one wants to solve the Reynolds equations, it is important to

ﬁnd additional relationships for these correlations of the turbulent veloc-

ity ﬂuctuations

. These relationships can be formulated by hypothetical

assumptions, and this approach played an important role in the past when

setting up turbulence models. Today, however, it is considered for certain that

reliable information on the time-averaged properties of turbulent ﬂows can

only be obtained by detailed experimental investigations of diﬀerent ﬂows. To

gain the necessary information requires local measurements of the instanta-

neous velocity of turbulent ﬂows. Such measurements can be made by means

of hot-wire or hot-ﬁlm anemometry and laser Doppler anemometry that pos-

sess the necessary resolution in terms of time and space for local velocity

measurements in ﬂows. These methods also permit to carry out the neces-

sary measurements in a relatively short time. Such measurements contribute

to the understanding of the physics of turbulent ﬂows and make it possible

to introduce additional information into the computations of turbulent ﬂows

for the above-mentioned correlations of turbulent velocity ﬂuctuations.

653

654 21 Introduction to Fluid-Flow Measurement

For measurements in wall-boundary layers, hot-wire and hot-ﬁlm anemo-

meters have been applied with great success for determining the mean

velocities U

and the ﬂuctuation velocity correlations u

. Depending on

their characteristic properties, many turbulent ﬂows can be investigated by

means of hot-wire and hot-ﬁlm anemometers. However, in the case of thin

boundary layers, inherent perturbations can occur which are caused by the

measuring sensors introduced for velocity measurements. Special designs of

measuring sensors are required to keep these measuring errors at a low level in

wall-bound boundary layers. Turbulent ﬂows also occur in regions with back

ﬂow, and these regions possess a number of properties which prevent the em-

ployment of hot-wire anemometers for precise measurements, or limit their

application to only some ﬂows. Of these properties of hot wires and hot ﬁlms,

that negatively inﬂuence the measurements, only the perturbing inﬂuence of

the hot-wire support on the actual measurement is mentioned. In addition,

high turbulence intensity in regions of ﬂow separation should be mentioned,

which leads to insurmountable diﬃculties concerning the interpretation of

the hot-wire signals.

Hot-wire and hot-ﬁlm measuring devices are based on measurements of

the convective heat transfer that occurs due to the ﬂuid ﬂowing over heated

elements and providing in this way a measure for the local ﬂow velocity.

These measurements, however, require the sensor to possess a higher tem-

perature than the ﬂuid, which can lead in liquid ﬂows to decomposition of

the ﬂuid medium. This is indicated in Fig. 21.1 by means of a photographic

recording published by Eckelmann [21.9]. Diﬃculties with the employment of

hot-wire and hot-ﬁlm anemometers, such as one encounters in measurements

in industrial conditions, are likewise indicated in Fig. 21.1. When giving up

the strict control of the particles carried along in the ﬂuid medium, natural

Flows with recirculation

Sensor lies in the wake of its own support

Deposition of solids on the

measuring sensor in dirty fluids

Disturbance due to small

bubles in a liquid flow

Fig. 21.1 Diﬃculties when employing hot-wire and hot-ﬁlm anemometers