Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

21.5 Basics of Hot-Wire Anemometry 675

By addition and subtraction it is possible, as the above equations show, to

determine the instantaneous U and W components of the velocity ﬁeld.

In practice, it is also usual to employ three-wire probes, in order to measure

all three velocity components simultaneously. At this point, we only want to

mention this fact. It is the object of this section of the book, to give an

introduction to ﬂow-measurement technology and for this purpose the above

references to a few hot-wire probe geometries suﬃce.

For boundary-layer investigations, it is extremely important to carry out

measurements close to walls. For such investigations probes with wire holders

are employed, which are formed in such a way that they permit measure-

ments near to the walls. Such a probe with specially formed prongs is shown

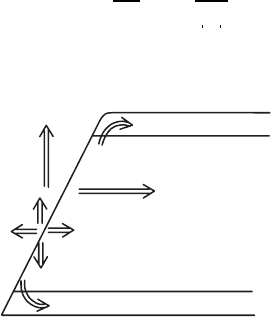
in Fig. 21.22. It is oriented such that the u component of the ﬂuid is mea-

sured. Traversing takes place in the y direction, to obtain the U velocity

proﬁle.

Diﬀerent demands are placed on the geometry of the hot-wire probes.

In order to keep the inevitable introduction of disturbances into the ﬂow

by hot-wire probes low and to obtain a good spatial resolution and a high

vibration resistivity of the probe, the probes should, on the one hand, have

probe lengths as short as possible. On the other hand, in order to reduce

the disturbing inﬂuence of the prongs, a large distance between the prongs

would be required. Small wire diameters are required for high resolution in

terms of time and space. Large diameters, on the other hand, ensure high

mechanical strength and smaller wire strains when mechanically stressed. By

compromising, nowadays optimized probes are available which permit reliable

measurements by means of hot-wire anemometers.

= U

= V

Spacer

Hot-wire lies

parallel to wall

Origin of

coordinate system

Fig. 21.22 Probe for boundary-layer investigations with special prong arrangement

676 21 Introduction to Fluid-Flow Measurement

21.5.4 Cooling Laws for Hot-Wire Probes

The basis for determining the ﬂow velocity by means of hot-wire probes,

is the heat transfer from the heated sensor to the medium ﬂowing around

the sensor. The heat can be transferred from the sensor by radiation

conduction

,freeconvection

, and especially by forced convection

con

(Fig. 21.23).

In the thermal equilibrium state, the supplied electric power is

= IE = I

R = E

/R (21.9)

equal to the heat output carried oﬀ by the sensor:

R =

con

(21.10)

The radiant heat

RSt

can be computed according to the equation:

= kσA

− T

, (21.11)

where σ is the Stefan–Boltzmann constant, A the heat-radiating surface of

the sensor, T is the operating temperature and T

the temperature of the

ﬂow medium. The factor k is at around 0.1 and takes into account that the

radiation of hot wires amounts to about 10%, at the very most, of the radi-

ation that a black body of equal dimensions would have. Except for extreme

cases, the heat loss of hot wires due to radiation can be neglected, as it is

only a small percentage of the heat which is transferred from the sensor by

forced convection.

The heat conduction

from the hot sensor into the cold prongs is,

according to Fourier:

= −2λ





πd





end of sensor

, (21.12)

con

•

Free convection

= Heat conduction

Heat conduction

= Heat radiation

= Forced convection

Prong B

Prong A

Fig. 21.23 Heat balance at the sensor in general form

21.5 Basics of Hot-Wire Anemometry 677

where λ

is the heat conductivity of the wire, d thewirediameteranddT/dx

the temperature gradient. The factor 2 before λ

, is present because of the

two prongs needed to hold the wire. For computing

, it is necessary to know

the temperature gradient at the wire ends. The temperature variation along

the sensor depends implicitly on the dimensionless heat-transfer coeﬃcient

expressed by the Nusselt number (Nu). With hot-wire probes, the heat loss

, the so-called wire end loss to the prong, amounts to about 10–20% of the

total heat loss from the sensor. Seen relatively, this proportion is the larger

the smaller is the ratio of wire length to wire diameter.

The heat carried oﬀ from the sensor, due to free convection

, gains in

importance when the buoyancy forces acting on the ﬂuid ﬂow considerably

inﬂuence the ﬂow ﬁeld around the wire. The characteristic dimensionless

quantity, which allows one to describe this inﬂuence, is the Grashof number:

Gr =

gβ∆TL

, (21.13)

where g is the gravitation acceleration, β is the compressibility coeﬃcient, ν

is the kinetic viscosity and ∆T is the wire overheating temperature.

According to Collis and Williams (1959), free convection can be neglected

in the case when

Re > Gr

1/3

(21.14)

The Grashof number, e.g. for a hot wire of 2.5 µm diameter in an air stream

at 300 K is about 6 ×10

−7

; therefore, for Reynolds numbers larger than 0.01,

no considerable free convection eﬀects on the heat transfer of a hot wire are

to be expected. This means that for the usually employed hot wires in air,

free convection can be neglected at ﬂow velocities larger than 0.1 m s

−1

In the case of velocity measurements with hot wires, the dominating heat-

transfer component from the wire to the ﬂow medium surrounding it, takes

place by forced convection

con

. The latter can be calculated as follows:

con

= απld(T − T

), (21.15)

where T is the wire temperature, d =2r is the wire diameter, l is the wire

length, T

is the ﬂuid temperature and α is the heat-transfer coeﬃcient. It

can be computed with the help of the Fourier law:

= −λl

2π



∂T

∂r



r=R

R dϕ, (21.16)

where λ is the heat conduction of the ﬂuid.

The dimensionless heat-transfer coeﬃcient at the sensor is deﬁned as

Nu =

αd

(Nusselt number) (21.17)

678 21 Introduction to Fluid-Flow Measurement

From the above two equations, the heat transfer by convection

con

can be

computed as

con

= Nuπlλ(T − T

) (21.18)

Thus a simpliﬁed energy balance at the hot-wire sensor reads

=2λA



wire end

+ Nuπlλ(T − T

) (21.19)

For handling this equation further, a general heat-transfer law has to be for-

mulated for hot-wire probes. The similarity theory of heat transfer states that

for geometrically similar ﬂow and heat transfer problems, the temperature

and velocity ﬁelds are similar, when the dimensionless characteristic quanti-

ties are equal. In general, the heat-transfer laws are described by relationships

between the Reynolds, Prandtl, Mach, Grashof and Knudsen numbers, of the

length-to-diameter ratio of the sensor elements, the overheating ratio, the

orientation of the probe in the ﬂow ﬁeld and other parameters.

Nu = Nu( Re, Pr, Gr, Ma, Kn, l/d, ∆T ...)

ﬂow ﬂuid buoyancy compress- inﬂuence geometry overheating

inﬂuence characteristics inﬂuence ability of the of the of the

inﬂuence molecule sensor hot wire

structure

For general considerations, the Nusselt number would have to be determined

individually for every ﬂow ﬁeld examined and the probe employed, in order

to formulate generally a law that takes into account the above complexity of

the dependencies.

For practical applications of hot-wire anemometry in gas ﬂows, the ﬂow

velocities are usually higher than 0.1 m s

−1

, and the inﬂuence of the Grashof

number on the heat transfer must therefore not be taken into account. The

same holds for the Mach number inﬂuence of the ﬂow. When this characteris-

tic number does not exceed a certain limit, e.g. Ma ≈ 0.3, the compressibility

eﬀects on the heat transfer can be neglected. Only in special cases, such as

in strongly diluted gases, e.g. in measurements of wind speeds at high atmo-

spheric altitudes, the diameter of the sensor can be equal to or even smaller

than the free pathlength of the molecules. In the normal case, ! (mean free

path of the molecules)  d (wire diameter), i.e. the heat transfer from the

hot wires is not inﬂuenced by the Knudsen number, i.e. for all measurements

continuum mechanics is applicable.

Moreover, assuming a large length-to-diameter relation of the consid-

ered hot wire [l/d > 400], the heat transfer is two-dimensional. With these

assumptions, the “Nusselt number dependence” reads:

Nu = Nu(Re,Pr,∆T,...) (21.20)

In spite of these introduced simpliﬁcations, it is very diﬃcult to formulate a

general law for the heat transfer by theoretical means. The heat transfer from

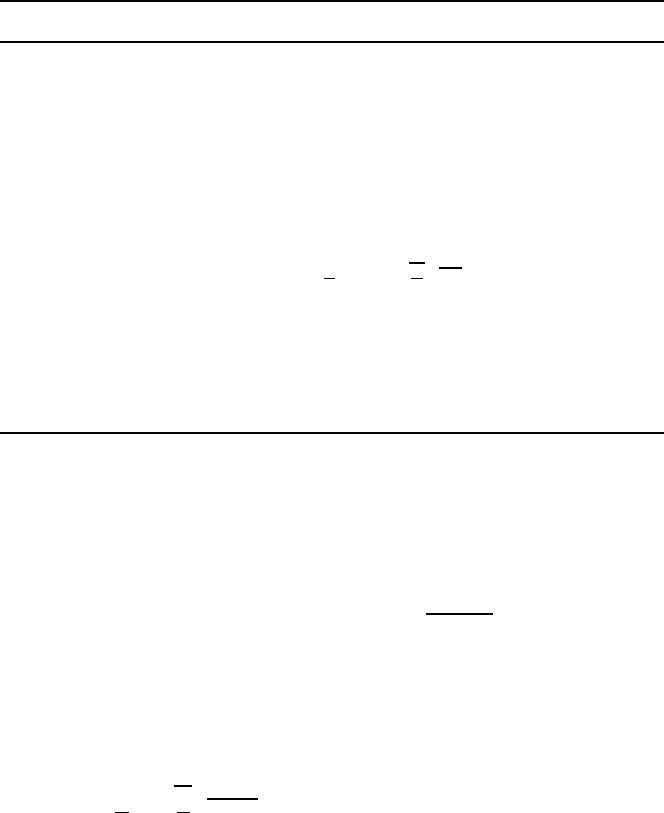
21.5 Basics of Hot-Wire Anemometry 679

Table 21.1 Heat-transfer laws

Reference Validity ABns

range

Collis and 0.02<Re<44 0.24 0.56 0.45 0.17 inﬂuence

Williams (1959) 0.02<Re<140 0 0.48 0.51 0.17 of the

temperature

Hilpert (1933) 1<Re<4 0 0.89 0.33 0

4<Re<40 0 0.82 0.38 0

40<Re<4,000 0 0.61 0.46 0

1<Re<4 0 0.872 0.330 0.0825 inﬂuence

4<Re<40 0 0.802 0.385 0.09625 of

40<Re<4,000 0 0.600 0.466 0.1165 the

temperature

King (1914) Pe = RePr  1



√

Pr 0.5 0 for Pr  1

Koch and Re <4.2 0.72 0.80 0.45 −0.67

Gartshore

(1972)

Kramers (1946) 0.01<Re<1,000 0.42 Pr

0.2

0.5 Pr

0.33

0.5 0

McAdams 0.1<Re<1,000 0.32 0.43 0.52 0

the hot-wire sensor is determined by the complex ﬂow ﬁeld which is developed

near the wires. Some of the heat-transfer laws, formulated and available in the

literature, are stated in Table 21.1. They are stated considering the following

form of a ﬁtted relationship:

Nu =[A (Pr,∆T)+b (Pr,∆T) Re

]



T − T



(21.21)

The constants used in (21.21) are given in Table 21.1.

Already in 1914 King formulated in his research work, which was funda-

mental for hot-wire technology, a theoretical solution for the heat transfer

from an evenly heated inﬁnitely long cylinder, assuming a two-dimensional

incompressible and friction-free potential ﬂow:

Nu =

√

RePr valid for ReP r = Pe >0.08 (21.22)

This relationship obtained by King (1914) for the Nusselt number is still em-

ployed today in experimental hot-wire anemometry, not in the above original

form, but in a modiﬁed form which is better suited for ﬂow measurements.

In practical applications it computes successfully, with empirically found

coeﬃcients, the heat transfer laws for hot wires.

If one has decided on an independent representation of the experimental

data by a known heat-transfer law, or having found laws of one’s own in an

investigated ﬂow medium for a particular hot-wire probe, one can easily ob-

tain the anemometer output voltage (measurement value) from a simpliﬁed

680 21 Introduction to Fluid-Flow Measurement

energy balance. The heat-transfer law formulated by McAdams, for exam-

ple becomes, in this manner, the fundamental relationship for ﬂow velocity

measurements:

/R = λ

π d



End of the wire

+0.32πlλ (T − T

)

+0.43πRlλ(T − T

)





0.52

(21.23)

The fundamental procedure, when determining the ﬂow velocity from a hot-

wire measurement, would then be the following. For a certain hot-wire probe,

with known geometric parameters d, l and operating values R (wire re-

sistivity) or T , one obtains the voltage-velocity function dependent on the

temperature, the pressure and the thermodynamic properties of the ﬂow

medium, in addition the excess temperature T − T

and the temperature

gradients at the sensor end. Knowing these parameters, the desired veloc-

ity behavior can be determined from the measured voltage behavior. After

all these explanations, it is worth mentioning that in practical hot-wire

anemometry direct calibration of the hot-wire sensor is preferred.

21.5.5 Static Calibration of Hot-Wire Probes

The approach described above for determining the heat loss of hot wires

permits the velocity behavior to be determined, for velocity measurements,

without calibration. However, for this purpose the geometric dimensions of

the measuring sensors and the operating values of the entire anemometer

have to be known precisely. Experience has shown, however, that a precise

knowledge of all the inﬂuencing quantities cannot be obtained with suﬃcient

precision for the commercially available hot-wire probes. Because of the com-

plicated processes, when drawing thin wires, the diameter of the active sensor

element, to give only one reason, cannot be obtained with high accuracy. Un-

certainties also occur when determining the sensor length, due to the welding

of the wire to the prongs. There are also other inﬂuences acting on the validity

of analytical heat-transfer laws, such as aging of the wire material, homo-

geneity of the wire alloy and corrosion of the sensor material. For all these

reasons, in measurement practice, preference is given to the experimental de-

termination of the voltage-velocity function in suitable calibration channels,

i.e. the hot wire is directly calibrated and then employed for measurements.

The probe considered for ﬂow investigations is placed in a low-turbulence

airstream of known and adjustable velocities and the anemometer output

voltage E, as a function of the ﬂow velocity U , is determined in the range

considered for the planned measurements, employing the calibrated sensor.

The static calibration curve, determined in this way, is obtained by plot-

ting the anemometer output voltage as a function of the known calibration

21.5 Basics of Hot-Wire Anemometry 681

Influence of free

convection

E =A+BU

Convection

dominated range

Influence of free

convection

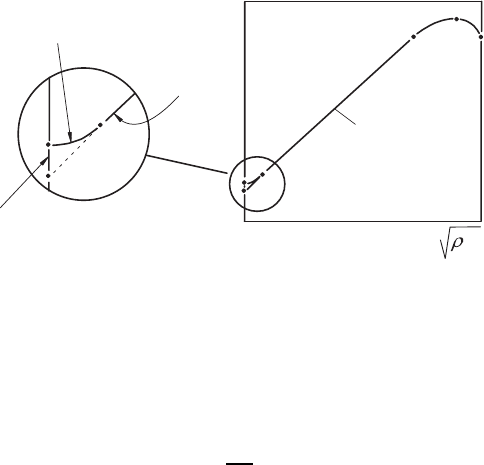
Fig. 21.24 Fundamental diagram of the calibration curve of a hot-wire probe

velocity. There is a non-linear dependence of the anemometer output voltage

on the ﬂow velocity.

In order to study the heat transfer from hot-wire sensors over a wide

velocity range, i.e. from very low velocities up to high velocities, but Ma <

0, 3, the supplied electric energy, which is proportional to the square of the

voltage, is plotted as a function of

√

ρU (Norman, 1967). The reasons for this

type of plotting will be discussed later, but equation (21.24) already makes

clear the necessity for this type of functional behavior.

One can divide the calibration curve into sub-ranges which physically

obey diﬀerent laws. The sub-range of the calibration curve between L and

M in Fig. 21.24 is important for air ﬂows in practical ﬂow cases. It can be

approximated analytically as follows:

= A + BU

(21.24)

This relationship is just a modiﬁcation of King’s law for the heat loss from a

heated cylinder. One has thus taken over, for explaining Fig. 21.24, the funda-

mentally existing analytical function between the energy loss and the velocity

of King’s equation. The parameters A, B and n are determined by calibra-

tion, as all the assumptions made by King with regard to the properties of

sensors are not known in practice, or do not apply exactly. In the area L to M

in Fig. 21.24, A, B and n are almost constant, as results from measurements.

In the sub-range of the calibration curve between K and L free convection

dominates. With increasing ﬂow velocity or, more precisely, with increasing

Mach number, the probe reaches its maximum cooling, and then decreases

with further increase of the Mach number. In the sub-range M–N –Q,itis

not possible to attribute only one velocity value to each measured value E,

i.e. the function in this area is not unique. In measuring practice the hot wire

is often employed only in the range L–M.

As the calibration of an employed hot-wire anemometer is every-day rou-

tine work for a ﬂow-measurement technician, it is necessary to explain step

682 21 Introduction to Fluid-Flow Measurement

Sensor

Pressure measurement

To anemometer

Calibration principle

(U - U ) =

Pressure measurement

Compressed air

To anemometer

Compressed air

Fig. 21.25 Calibration channels with mounted hot-wire probe and pressure

measuring device

by step how to proceed in calibrating a commercially available hot-wire

anemometer in an air jet. The probe is mounted, for the calibration, directly

in or shortly after the nozzle outlet of a calibration channel (Fig. 21.25). The

hot-wire sensor is oriented towards the outcoming ﬂow. It is thus ensured

thattheprobeislocatedinanareaofuniformvelocityandlowturbulence

intensity. In this region, the geometry of the nozzle also deﬁnes the ﬂow

direction.

The calibration of a hot wire is carried out for many velocity points over the

entire velocity range that is of interest for a particular set of measurements.

For ﬂow velocities that are not too low and not too high, as mentioned above

the calibration follows a law as given by Fig. 21.24. Practical application of a

calibrated hot wire is often limited to the range where this simple analytical

expression for the E = f(U) dependence can be found, i.e. to the L–M range

in Fig. 21.24.

The following data serve as an example of a typical velocity calibration.

The room temperature for these measurements was t

Atm

=19.5

◦

Candthe

atmospheric pressure was p

Atm

= 756 mmHg.

The measured anemometer output voltages E and the pressure diﬀerence

read from the manometer and the atmospheric pressure, ∆p,aregiveninthe

ﬁrst two lines of Table 21.2.

To evaluate the E

(U) relationship from the data given in Table 21.2,

the calibration velocity U has to be computed from the measured pressure

diﬀerences ∆p. Assuming an incompressible friction-free ﬂow, the Bernoulli

theorem between the cross-sections in front of and directly behind the

calibration nozzle reads

+ p

+ p (21.25)

With p = p

Atm

and p

− p

Atm

= ∆p,oneobtains:

∆p =

− U

(21.26)

21.5 Basics of Hot-Wire Anemometry 683

Table 21.2 Typical data of a hot-wire calibration

Anemometer Nozzle pressure ∆p Calibration velocity E

0.4356

output at manometer (m s

−1

)

voltage (V) (mm W

−1

) U = 1.2821



∆p (mm W

−1

) × 9.8066

2.88 1.04 4.09 8.29 1.85

3.01 2.11 5.83 9.06 2.15

3.16 4.24 8.27 9.98 2.51

3.28 7.20 10.77 10.76 2.82

3.36 10.25 12.85 11.29 3.04

3.46 15.20 15.65 11.97 3.31

3.54 20.17 18.03 12.53 3.52

3.62 27.42 21.02 13.10 3.77

3.68 33.47 23.23 13.54 3.93

3.73 39.88 25.35 13.91 4.09

3.79 43.34 27.62 14.36 4.24

3.83 54.

53 29.65 14.67 4.38

3.90 67.26 32.93 15.21 4.58

When the area ratio of the nozzle inlet to the nozzle outlet is larger than

1:16, as in the present calibration, the velocity U

in the above equation

can be neglected without great loss of accuracy. Hence, one obtains for the

calibration velocity from the ∆p measurements:

U =

∆p (21.27)

The density of the air, which is not known yet, can be computed from the

law for ideal gases:

p = ρRT (21.28)

Under the calibration conditions mentioned here, ρ is given by:

ρ =

Atm

756 × 133.3

283 (273 + 19.5)

=1.2167 N s

−4

(21.29)

with 133.3Nm

−2

/mmHg = 1; R

air

= 283 m

−2

−1

With this result, the calibration velocity can be computed:

U =1.2821



∆p , (21.30)

where

√

∆p represents the pressure diﬀerence read from the manome-

ter. In the above equation, ∆p has to be multiplied by 9.8066

(1 mm W s ˆ=9.8066 n m

−2

) and then only the root has to be extracted

and ﬁnally to be multiplied by 1.2821. In this way, one obtains the calibra-

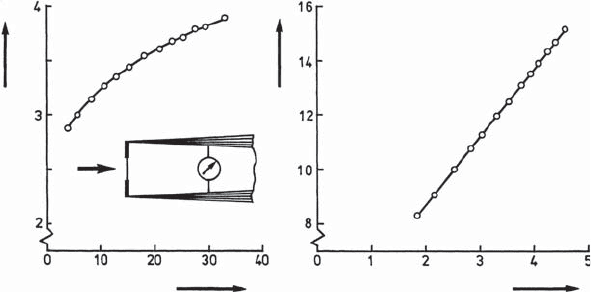
tion velocities stated in the third column of Table 21.2. Figure 21.26 shows a

typical calibration curve of a hot-wire probe. It was obtained by plotting the

voltage measured at the anemometer outlet as a function of the computed

calibration velocities.

684 21 Introduction to Fluid-Flow Measurement

E =

3,6542

2,5147

0,4356

[Volt]

[m/s]

Fig. 21.26 Calibration curve taken during calibration, in two manners of

representation

The application of hot-wire anemometers to determine the local velocity

of a ﬂuid ﬂow from voltage measurements, is occasionally helped by applying

an analytical expression for the voltage-velocity laws. As already mentioned,

in the velocity range investigated here, this law can be represented by the

modiﬁed King law:

= A + BU

(21.31)

The calibration task lies in the determination of the constants A, B and n

from the measured data. This can be done graphically, by plotting the square

of the anemometer output voltage against U

. However, the exponent n is not

known a priori, so that a variation of n is required, until the correct exponent

n yields the measurement points lying on a straight line. The exponent n

depends somewhat on the ﬂow velocity; in a limited velocity range a constant

exponent n can be deﬁned, however. The gradient of the straight line in the

− U

diagram corresponds to the constant B. The voltage value in the

point of intersection of the extrapolated straight line and the E axis provides

the constant A.

The values for the constants A, B, n can also be determined numerically.

In an iteration procedure, the exponent n is changed systematically, and for

each n value the other remaining constants A and B are evaluated from

the calibration data by applying the method of least-squares ﬁt. When a

minimum of the “square of errors” between the analytical expression and the

calibration data is obtained, A, B and n are taken as best ﬁts.

Finally it should be emphasized that the constant A does not agree with

the output voltage of the anemometer at zero velocity. This is understandable,

as two diﬀering mechanisms of heat transfer deﬁne this quantity. In the case of

the E

measurement at U = 0, the heat release by free convection dominates

and in the case of extrapolation of the data to U = 0, the heat release is due

to forced convection.