Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

634 20 Fluid Flows with Heat Transfer

predeﬁned and did not enter into the ﬂuid-mechanical considerations of the

quantities of the ﬂow problem as unknowns that were to be computed. Thus

the complexity of ﬂow-problem solutions was considerably reduced, as with

constant values for ρ, µ and λ the strong coupling between the momentum

equations and the energy equation was broken. For the solution of ﬂow prob-

lems, it was therefore suﬃcient to solve the continuity and the momentum

equations, i.e. the energy equation had only to be employed when, in addition

to the knowledge of the ﬂow ﬁeld, information on the temperature ﬁeld of

the ﬂuid was needed.

In this section, a ﬂow problem will be considered for which it is no longer

permissible to neglect the density modiﬁcations that occur. Restrictively, it

will be assumed, however, that only small density modiﬁcations arise, so that

the following holds:

ρ = ρ

+ ∆ρ ≈ ρ

[1 − β

(T − T

)] with β

= −



∂ρ

∂T



. (20.36)

With this, the equations of ﬂuid mechanics can be stated as follows:

∂U

∂x

=0, (20.37)



∂U

∂t

+ U

∂U

∂x



= −

∂

∂x

(P − ρ

)+µ

∂

∂x

+(ρ − ρ

) g

, (20.38)

(ρ − ρ

)=−ρ

(T − T

), (20.39)

∂T

∂t

+ U

∂T

∂x





∂

∂x

. (20.40)

These equations can be employed for examining ﬂows driven by density

diﬀerences, i.e. with the above set of partial diﬀerential equations natural

convection ﬂows can be described mathematically.

From these equations, one obtains for two-dimensional ﬂow conditions

∂/∂x

(...) = 0, and for fully developed ﬂows ∂/∂x

) = 0, the following

simpliﬁed equations:

• Momentum equation:

∂U

∂t

= −

∂Π

∂x

+ ρgβ

(T − T

)+µ

∂

∂x

. (20.41)

• Energy equation:

ρc

∂T

∂t

= λ

∂

∂x

+ µ





(20.42)

20.3 Natural Convection Flow 635

Fig. 20.5 Free convective ﬂow between

vertical plates

Wall

Upwards

directed flow

Downwards

directed flow

T =

T(x

)

where, concerning the axial directions, the coordinate system stated in

Fig. 20.5 was chosen.

Equations (20.41) and (20.42) can now be simpliﬁed for stationary

ﬂows, that run without an external pressure gradient, i.e. ∂Π/∂x

=0.

For such ﬂows, the basic equations describing natural convection hold as

follows:

• Momentum equation:

0=ρgβ

(T − T

)+µ

. (20.43)

• Energy equation:

ρc





. (20.44)

For the ﬂow driven by natural convection between two plates, the momentum

equation results in the following form:

0=µ

+ ρ

gβ

(T − T

) (20.45)

and the energy equation, taking into consideration the above assumption,

can be written as:

0=λ

+ µ





, (20.46)

where T

=1/2(T

+ T

). The subsequent boundary conditions describe

the natural convection ﬂow problem sketched in Fig. 20.5:

636 20 Fluid Flows with Heat Transfer

(D)=U

(−D)=0, (20.47)

T (D)=T

; T (−D)=T

. (20.48)

Introducing the so-called buoyancy-viscosity parameter A:

A =

gµD

(20.49)

the basic equations can be normalized as stated below, introducing the

following dimensionless quantities:

∗

= x

/D; U

∗

ρDU

; T

∗

(T − T

)

− T

)

. (20.50)

One obtains in this way the following dimensionless equations for the

resultant velocity and temperature distribution:

∗

= −GrT

∗

and

∗

= −

, (20.51)

where the Grashof number Gr results from the derivations as follows:

Gr =

gρ

β (T

− T

)

. (20.52)

When considering that the buoyancy-viscosity parameter A assumes very

small values for most ﬂuids and that moreover Gr assumes large values

for buoyancy-driven ﬂows, relevant in practice, then for the dimensionless

temperature distribution, the following is obtained to a good approximation:

∗

=0 ; T

∗

= C

∗

+ C

. (20.53)

With T

∗

= −1forx

∗

= −1andT

∗

=1forx

∗

= 1 one obtains C

=1and

=0andthus

∗

= x

∗

(20.54)

∗

inserted in (20.51) yields

∗

= −Grx

∗

and hence U

∗

= −

∗3

+ C

∗

+ C

. (20.55)

With the boundary conditions at x

∗

=1:U

∗

=0andatx

∗

= −1: U

∗

=0,

one obtains C

= Gr/6andC

=0andthus

∗

− x

∗3

. (20.56)

The resulting temperature distribution emerges from this analysis as linear. It

thus represents the distribution typical for pure heat conduction. On the other

hand, the velocity distribution is described by a point-symmetrical cubic

function as sketched in Fig. 20.5. Along the wall with the higher temperature,

an upward directed ﬂow forms, and on the side of the cool wall a ﬂow forms

that is directed downwards. Flows of this kind can occur between the planes

of insulating-glass windows when these have been dimensioned incorrectly.

20.4 Non-Stationary Free Convection Flow 637

20.4 Non-Stationary Free Convection Flow Near

a Plane Vertical Plate

The combined ﬂow and heat-transfer problem discussed in this section, deals

with the diﬀusion of heat from a vertical wall, heated suddenly and brought

to a temperature T

at time t = 0. The diﬀusion of heat takes place into an

inﬁnitely extended ﬁeld extending into a half-plane. The density modiﬁcations

in the ﬂuid, caused by the heat diﬀusion, result in buoyancy forces, and these

in turn lead to a ﬂuid movement that can be treated analytically as a free

convection ﬂow. With it the basic equations, expanded in the momentum

equations by the Oberbeck/Bussinesq terms as stated in Sect. 20.3, can be

given as indicated below in the form of a system of one-dimensional equations.

Basically equations result for an unsteady ﬂow providing a basis for the sought

solution. In this context the following was taken into consideration:

• Because of ∂U

/∂x

= 0, due to the fully developed ﬂow in the x

direction,

one obtains from the two-dimensional continuity equation U

= constant.

As U

= 0 at the wall is given, one obtains U

= 0 in the entire ﬂow area.

• With the above insights, the left-hand side of the x

momentum equation

reduces to the term ρ

(∂U

/∂t), so that the following system of equations

holds for the considered natural convective ﬂow problem:

– Momentum equation:

∂U

∂t

= µ

∂

∂x

+(ρ − ρ

)g. (20.57)

– Energy equation:

p,0

∂T

∂t

= λ

∂

∂x

. (20.58)

The dissipation term in the energy equation µ (dU

/dx

)

was neglected here

for reasons stated in Sect. 20.3. For further details, see also ref. [20.4].

For the further explanation of the problem to be examined here, it should

be said that for all times t<0 the following holds: U

,t)=0and

T (x

,t)=T

for x

≥ 0, i.e. in the entire area ﬁlled with ﬂuid there is

initially no ﬂow, and the ﬂuid has the same temperature everywhere.

For all times t ≥ 0, the following boundary conditions will hold: U

(0,t)=0

(no-slip condition at the wall) and T (0,t)=T

(sudden increase of the wall

temperature). Moreover, the ﬂow problem to be examined is described for

→∞by U

(∞,t)=0andT (∞,t)=T

The velocity and temperature ﬁelds sketched in Fig. 20.6 indicate the dif-

fusion processes that take place and how they contribute to the initiation of

the described buoyancy ﬂow. The molecular diﬀusion of the temperature ﬁeld

is evident, together with the induced ﬂuid movement and the momentum loss

to the wall. Important for the quantitative information to be derived here is

the presence of an analytical solution of the buoyancy problem indicated in

Fig. 20.6.

638 20 Fluid Flows with Heat Transfer

Fig. 20.6 Unsteady natural convection

ﬂow at a ﬂat vertical plate

The above ﬂow problem has to be solved as a one-dimensional, unsteady

natural convection ﬂow problem, namely as a similarity solution of the equa-

tion system (20.57) and (20.58). To derive the solution, we introduce the

similarity variable:

η =

√

(20.59)

and for the dependent variables U

,t)andT (x

,t)forx

≥ 0 the similarity

ansatz:

,t)=[β

− T

) gt] F (η) (20.60)

and

T (x

,t)=(T

− T

) G (η) . (20.61)

These ansatzes are introduced in this particular form with the aim of con-

serving the dimensionless forms of the diﬀerential equations describing the

problem and, moreover, to transfer the partial diﬀerential equations into

ordinary diﬀerential equations.

The above ansatzes (20.60) and (20.61) hold for Pr =1andaresolved

below for this special case. More general solutions for Pr =0weregiven

by Illingworth [20.1] and can be looked up there. The special case discussed

here suﬃces to introduce students of ﬂuid mechanics to the ﬁeld of natural

convection ﬂows.

With the above similarity ansatz, one obtains for the derivative in the

diﬀerential equation for U

∂U

∂t

= ρ

− T

) g

∂

∂t

[tF (η)] (20.62)

or the derivative executed with respect to t:

∂U

∂t

= ρ

− T

) g



F −

ηF





. (20.63)

Similarly, for the ﬁrst derivative with respect to x

20.4 Non-Stationary Free Convection Flow 639

∂U

∂x

= µ

− T

) gtF



√

(20.64)

and thus for the second derivative:

∂

∂x

= µ

− T

) gtF



4ν

(20.65)

or in consideration of ν

=(µ

/ρ

) transcribed as:

∂

∂x

= ρ

− T

) g







. (20.66)

For the gravitation term in the U

diﬀerential equation, one obtains:

(ρ − ρ

)g = ρ

(T − Z

)g = ρ

− T

)gG(η). (20.67)

Insertion of (20.63), (20.66) and (20.67) into the momentum equation to be

solved, yields the following ordinary diﬀerential equation for F (η):



+2ηF



− 4F +4G =0. (20.68)

For the derivatives in the energy equation in terms of time, one obtains:

∂T

∂t

= ρ

− T

)

∂

∂t

[G(η)] (20.69)

and after carrying out the diﬀerentiation:

∂T

∂t

= ρ

− T

)



. (20.70)

Deriving the second derivative with respect to x

yields:

∂

∂x

= G



4µ

− T

) (20.71)

and for Pr =1

∂

∂x

= G



− T

). (20.72)

Insertion of (20.70) and (20.71) into the energy equation yields:



− 2ηG



=0. (20.73)

The boundary conditions for the solution of the above ordinary diﬀerential

equations (20.68) and (20.73) read:

=0:U

(0,t)=0 ; η =0:F (0) = 0

T (0,t)=T

; G(0) = 1

→∞: U

(∞,t)=0 ; η =1:F (1) = 0

T (∞,t)=T

; G(1) = 0

640 20 Fluid Flows with Heat Transfer

As a solution of the diﬀerential equation (20.73), one obtains:

G(η)=1− erf(η). (20.74)

The solution of the diﬀerential equation (20.68), with G(η) inserted, can be

obtained as a solution of the homogeneous diﬀerential equation for F (η):



+2ηF



− 4F = 0 (20.75)

and with the particular solution F (η)=erf(η) and adding the homogeneous

solution results in

F (η)=

√

η exp

−η

− 2η

erf(η). (20.76)

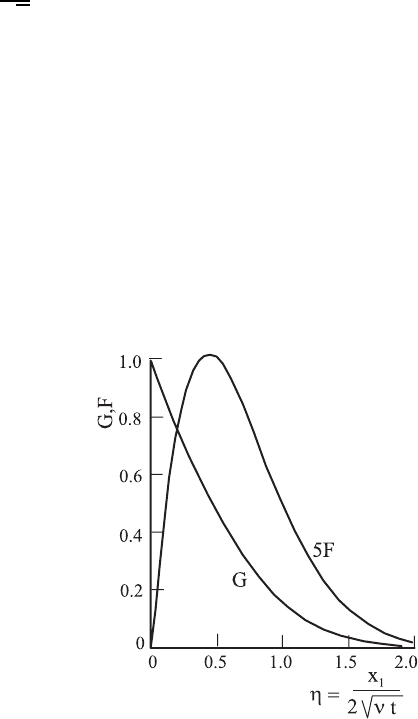
With this, the solutions for F and G, as shown in Fig. 20.7, can be determined

from (20.74) and (20.76). With a decrease in G with increase in η, a decrease

in temperature with increasing distance from the wall is indicated. The F (η)

distribution relates to the velocity distributions for the natural convection.

This convective ﬂow forms due to the buoyancy forces induced by density

diﬀerences near the wall.

The parts of the similarity solutions of the equation system (20.57) and

(20.58) represented in Fig. 20.7 show, on the one hand, the normalized tem-

perature proﬁle G(η) that develops due to the temperature diﬀusion from

Fig. 20.7 Solutions F (η)andG(η)for

the free convection ﬂow along a plane

vertical plate

20.5 Plane-Plate Boundary Layer 641

the heated wall into the ﬂuid. The ﬁgure shows, moreover, the standardized

velocity proﬁle, which is caused by buoyancy and which is strongly inﬂu-

enced by the molecule-dependent momentum loss to the wall. Because of the

assumed fully developed ﬂow in the x

direction, for the temperature ﬁeld

(20.61) and the velocity ﬁeld (20.60) physically convincing solutions result

from the diﬀerential equations. Altogether the ﬂow and temperature distri-

butions are understood as examples of many buoyancy ﬂows that exist in

nature in a large variety. For a number of these ﬂows, driven by temperature

ﬁelds, analytical solutions exist.

20.5 Plane-Plate Boundary Layer with Plate Heating

at Small Prandtl Numbers

In Chap. 16, the two-dimensional boundary-layer equations were derived from

the general Navier–Stokes equations according to a procedure suggested by

Prandtl. On extending these derivations to boundary-layer ﬂows with heat

transfer, one obtains on the following assumptions:

= ﬂow direction; x

= direction with ∂/∂x

(···)=0

the following equations for x

= x, x

= y, U

= U, U

= V :

Stationary Compressible Flows (Boundary-Layer Equations)

∂

∂x

(ρU)+

∂

∂x

(ρV )=0, (20.77)



∂U

∂x

+ V

∂U

∂y



= −

∂

∂y



∂U

∂y



+ ρg

β (T − T

∞

) , (20.78)

ρc



∂T

∂x

+ V

∂T

∂y



= U

+ λ

∂

∂y

+ µ



∂U

∂y



, (20.79)

ρ = constant or

= RT and µ = µ(T ),λ(T ),c

(T ). (20.80)

Hence, there are four diﬀerential equations for U, V , P , ρ and T ,whichcan

be solved with the boundary conditions deﬁning the respective problem. For

incompressible ﬂows, we obtain the following:

642 20 Fluid Flows with Heat Transfer

Stationary Incompressible Flows (Boundary-Layer Equations)

∂U

∂x

∂V

∂y

=0, (20.81)

∞



∂U

∂x

+ V

∂U

∂y



= −

+ µ

∞

∂

∂y

− ρ

∞

(T − T

∞

) , (20.82)

∞

p∞



∂T

∂x

+ V

∂T

∂y



= λ

∂

∂y

+ µ

∞



∂U

∂y



+ ρ

∞

(T − T

∞

) .

(20.83)

This system of partial diﬀerential equations can be solved for ρ = ρ

∞

constant, λ = λ

∞

= constant, c

= c

p∞

= constant and µ = µ

∞

= constant

for plane-plate boundary-layer ﬂows by including the boundary conditions

that characterize the ﬂow and heat-transfer problem, in order to compute U,

V and T . The externally imposed pressure gradient (dP/dx) can often be

assumed to be given for this kind of ﬂow.

In order to integrate the equations, it is recommended also to include in

the considerations the inﬂuence of the Prandtl number on the solution. Here,

it has to be taken into consideration that the Prandtl numbers of the ﬂuids

considered in this book, are able to cover the wide range that is indicated in

Fig. 20.8.

For boundary-layer ﬂows with very small Prandtl number, i.e. boundary

layers of melted metals, thermal boundary layers result, which are many

times thicker than the ﬂuid boundary layers (see Fig. 20.9). It is therefore

understandable that it is recommended, for small Prandtl numbers, to treat

boundary-layer ﬂows with heat transfer, such that the ﬂuid boundary layer

is entirely neglected. From the continuity equation (20.81), it follows that

the gradients of V in y direction and U in x direction are connected in the

following way:

∂V

∂y

= −

(20.84)

Prandtl number

Gases Water

Viscous oils

Liquid metals

Fig. 20.8 Domains of Prandtl numbers for diﬀerent ﬂuids (ﬂuids and gases)

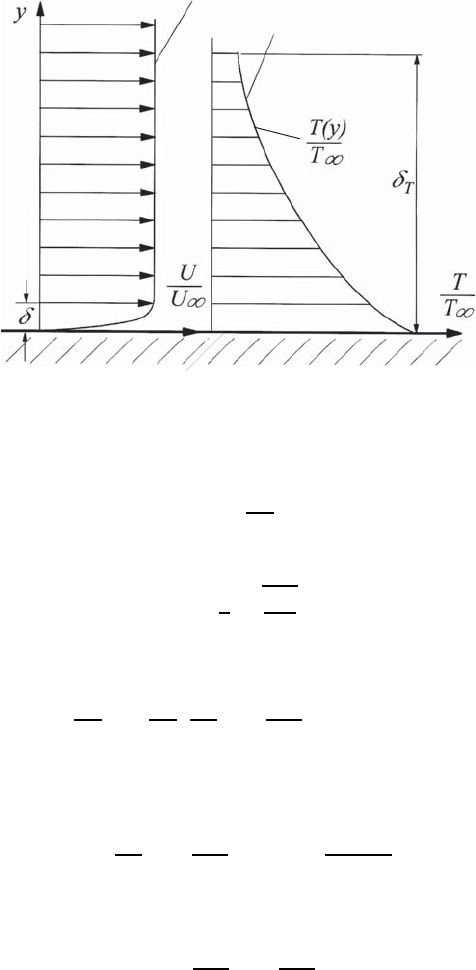
20.5 Plane-Plate Boundary Layer 643

Velocity distribution

Temperature distribution

Plate

Fig. 20.9 Thermal boundary layer and thermal boundary layer for small Prandtl

numbers

and thus

V = −

y. (20.85)

For the analytical considerations to be carried out, the similarity variable:

η =

∞

(20.86)

is introduced. From the energy equation, one obtains:

∂T

∂x

− y

∂T

∂y

= a

∂

∂y

(Pr << 1) . (20.87)

For T = T

for y =0andT = T

∞

for y →∞(and this for all x positions),

one obtains for a constant external ﬂow, i.e. U(x)=U

∞

= constant,

∞

∂T

∂x

= a

∂

∂y

with a =

∞

p,∞

. (20.88)

For the standardized temperature T

∗

=(T − T

∞

)/∆T

with ∆T

=(T

−

∞

), one obtains:

∞

∂T

∗

∂x

= a

∂T

∗

∂y

(20.89)

and with the similarity ansatz:

∗

= f(η) (20.90)