Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

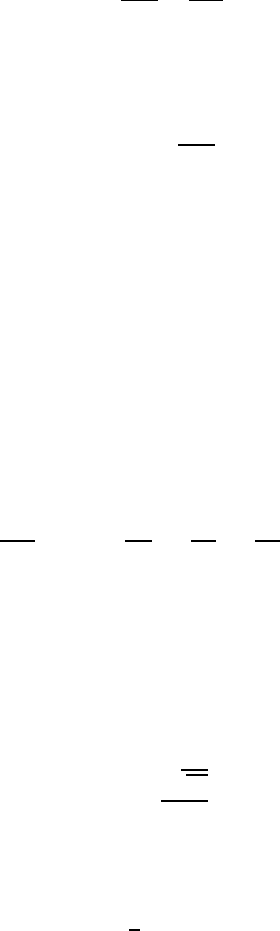
624 19 Numerical Solutions of the Basic Equations

where the velocity gradient is derived from the logarithmic law (19.129) and

the local shear tension is set equal to the wall shear stress.

The dissipation rate, which appears in the k equation (19.121), is

approximated by assuming a linear dependence of the near-wall length scale:

L =

3/2



3/4

n. (19.137)

Equation (19.137) holds under local equilibrium conditions and for a logarith-

mic velocity law. From this follows an equation for  in the near-wall control

volume in the form



= c

3/4

3/2

κn

. (19.138)

19.6.2.5 Dissipation Rate

According to the treatment of boundary conditions in practice, for the dis-

sipation rate , its value is determined at the ﬁrst computational node away

from the wall by employing (19.138).

19.6.2.6 Symmetry Planes

Along the symmetry planes (or symmetry lines) of ﬂow, the standard gradi-

ents (diﬀusive ﬂows) of the dependent variables and the normal velocity U

are set equal to zero:

∂U

∂n

= U

∂T

∂n

∂k

∂n

∂

∂n

=0. (19.139)

19.6.2.7 Inﬂow Planes

Usually inlet ﬂow proﬁles are derived from experimental data or from other

empirical information and are employed as inﬂow conditions. The turbu-

lence quantities often refer to the inﬂow velocity U

by specifying a relative

turbulence intensity Tu, deﬁned as

Tu=



. (19.140)

Typical values for Tu lie between 1 and 20%. For an isotropic turbulent ﬂow,

Tu is related to k through

k =

(TuU

)

. (19.141)

19.6 Computations of Turbulent Flows 625

At the inﬂow plane dissipation rates can be speciﬁed, assuming that the

quantity of the larger turbulence vortices is proportional to a typical scale of

length H of the cross ﬂow area, i.e.

 =

3/2

. (19.142)

Characteristic values for the proportional factor a are of the order of

magnitude of 0.01–1.

19.6.2.8 Outﬂow Planes

The same approach as described in Sect. 19.5.4, is usually employed for out-

ﬂow planes. In addition to the equations stated there, the gradients of k and

 assigned to the ﬂow direction are set to zero.

The above equations can now be solved numerically for two-dimensional

ﬂows, including the indicated boundary conditions. For the illustration

of typical computational results, diﬀerent ﬂow problems are shown in

Figs. 19.16–19.18.

Fig. 19.16 Flows around a near-ground model vehicle – computational result – LDA

measurements

Fig. 19.17 Subcritical ﬂow around a circular cylinder at Re =3,900; Breuer (2002)

626 19 Numerical Solutions of the Basic Equations

(a) (b)

Fig. 19.18 Separated ﬂow around a wing at Re =20,000; (a) non-stationary

rotational-power distribution; (b) time-averaged streamlines; Breuer (2002)

References

19.1. Sch¨afer, M.: Numerik im Maschinenbau, Springer, Berlin Heidelberg New York,

1999

19.2. Cebeci, T. and Bradshaw, P.: Physical and Computational Aspects of Convec-

tive Heat Transfer, Mei Ya Publications, Springer, Berlin Heidelberg New York,

Tokyo, 1984

19.3. Ferziger, J.L. and Peric, M.: Computational Methods for Fluid Dynamics, 2nd

revised edition, Springer, Berlin Heidelberg New York, 1999

19.4. Peyret, R. and Taylor, T.D.: Computational Methods for Fluid Flow, Springer

Series in Computational Physics, Springer, Berlin Heidelberg New York, 1983

19.5. Wilcox, D.C.: Turbulence Modeling, DCW Industries, Griﬃn Printing,

Glendale, CA, 1993

19.6. Laundes, B.E. and Spalding, D.B.: Mathematical Models of Turbulence,

Acadmic Press, London (1972)

Chapter 20

Fluid Flows with Heat Transfer

20.1 General Considerations

The derivations carried out in Chap. 5 to yield the basic equations of ﬂuid

mechanics also include considerations of the energy transport and, based on

these considerations, diﬀerent forms of the energy equation were derived.

There it could be shown that the local mechanical energy equation, stated as

a diﬀerential equation for a ﬂuid, does not represent an independent equation,

as it can be derived from the generally formulated momentum equation. This

was the reason to subtract this equation from the total energy equation, in

order to obtain the thermal energy equation that can be written as follows:



∂e

∂t

+ U

∂e

∂x



= −

∂ ˙q

∂x

− P

∂U

∂x

− τ

∂U

∂x

, (20.1)

where ρ is the density of the ﬂuid, e its inner energy, t the time, U

the ﬂuid

velocity, ˙q

the heat ﬂux, P the pressure and τ

the molecular-dependent

momentum transport. This equation can now be employed for a thermody-

namically ideal ﬂuid, i.e. for ρ = constant and thus for (∂U

/∂x

) = 0, and

also for

˙q

= −λ

∂T

∂x

and τ

= −µ



∂U

∂x

∂U

∂x



(20.2)

in the following form for heat transfer computations, where c

= c

= c =

was taken into consideration because of ρ = constant:

ρc



∂T

∂t

+ U

∂T

∂x



= λ

∂

∂x

+ µ



∂U

∂x



. (20.3)

Together with the continuity equation:

∂U

∂x

= 0 (20.4)

627

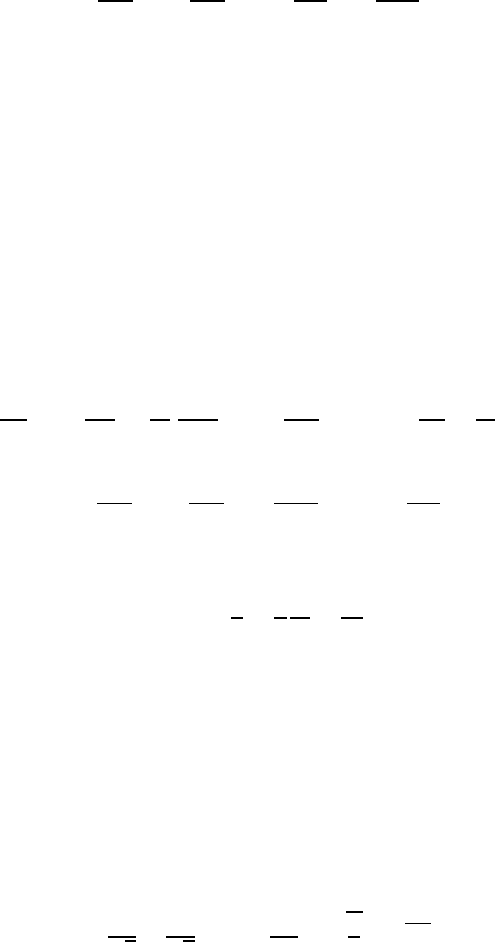
628 20 Fluid Flows with Heat Transfer

and the momentum equations for j =1, 2, 3:



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

+ µ

∂

∂x

+ ρg

(20.5)

one obtains a system of ﬁve diﬀerential equations for the ﬁve unknowns U

, U

, P and T , which can be solved with suitable boundary conditions.

Thus, ﬂow problems can be solved that occur coupled with heat-transfer

problems, but do not lead to considerable modiﬁcations of the ﬂuid properties

such as ρ, µ and λ. This is often the case in technical applications of ﬂuid

mechanics, where the actual ﬂuid ﬂow processes are sometimes of secondary

importance, the main importance being given to the heat transfer and heat

dissipation of a system. This signiﬁcance of heat transfer is the actual reason

for including the present chapter in a book on ﬂuid mechanics. It serves as

an introduction for students of ﬂuid mechanics into an important ﬁeld of

applications of ﬂuid-mechanical know-how.

In order to present, in an easily understandable way, some general proper-

ties of heat transfer, as compared with momentum transfer, equations (20.3)

and (20.5) are rearranged:

∂T

∂t

+ U

∂T

∂x

ρc

∂

∂x

+ ν



∂U

∂x



with

ρc

(20.6)

and

∂U

∂t

+ U

∂U

∂x

= ν

∂

∂x

+ ρg

−

∂P

∂x

, (20.7)

where ν is the viscous diﬀusion coeﬃcient and a = λ/ρc is the thermal

diﬀusion coeﬃcient. From their interrelationship, the Prandtl number results:

Pr =

ρc

µc

which expresses how the molecular-dependent momentum transport relates

to the molecular-dependent heat transport. The Prandtl number can thus

be employed to demonstrate in which way momentum transport and heat

transport relate relatively to one another.

For small Pr, e.g. for metallic melts for equal development lengths, the

thermal boundary layer of a plate ﬂow has developed more intensely than

the “velocity boundary layer” (Fig. 20.1).

The facts illustrated in Fig. 20.1 can also be expressed in development

lengths for momentum and temperature boundary layers, such that for δ

the following relationships hold:

√

;

√

Pr. (20.8)

For equal development length, the following results for the boundary layer

thicknesses can be derived:

20.1 General Considerations 629

U(y)

T(y)

Fig. 20.1 Thicknesses of temperature-boundary layers for diﬀerent Prandtl numbers

√

Pr. (20.9)

This means that the molecular-dependent momentum transport is larger than

the molecular-dependent heat transport when Pr > 1 (see Fig. 20.1).

When extending the similarity considerations in Chap. 7, where from the

dimensionless momentum and τ

transport equations:

∗

∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗

= −

∆P

∂P

∗

∂x

∗

−

∂τ

∗

∂x

∗

, (20.10)

∗

−µ

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

(20.11)

the following characteristic quantities of a ﬂow can be derived:

= u

and t

. (20.12)

When carrying out corresponding considerations for the energy equation, one

obtains the following derivations:

• Energy equation:

ρc



∂T

∂t

+ U



= −

∂q

∂x



∂P

∂t

+ U

∂P

∂x



− τ

∂U

∂x

. (20.13)

• Fourier law of heat transfer

= −λ

∂T

∂x

. (20.14)

630 20 Fluid Flows with Heat Transfer

• Dimensionless form of energy equation:

∗





∂T

∗

∂t

∗

+ U

∗

∂T

∗

∂x

∗



= −

˙q

)

∆T

∂ ˙q

∗

∂x

∗

−

∆P

)

∆T





∂P

∗

∂t

∗

+ U

∗

∂P

∗

∂x

∗



−

p,c

∆T

∗

∂U

∗

∂x

∗

. (20.15)

• Characteristic temperature diﬀerence and characteristic heat transport:

∆T

)

and ˙q

= τ

. (20.16)

• Characteristic units of length and time:

˙q

∗

= −

∆T

∗

∂T

∗

∂x

∗

; !



∆T

˙q

)





(20.17)

so that !

= !

/P r holds and t

= t

/P r . These derivations represent the

facts stated in Fig. 20.1 and in (20.8). These facts will turn up again in the

examples cited in the subsequent representations of ﬂows with heat transfer.

20.2 Stationary, Fully Developed Flow in Channels

A simple ﬂow with heat transfer is the stationary fully developed ﬂow in

channels with a wall in motion. In Fig. 20.2, the basic geometry of the two-

dimensional version of this ﬂow is sketched, and the boundary conditions are

also stated. For this ﬂow, the following equations for two-dimensional ﬂows

hold, given below for ρ = constant and for constant viscosity and constant

heat conductivity:

∂U

∂x

∂U

∂x

=0, (20.18)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



+ ρg

(20.19)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



+ ρg

(20.20)



∂T

∂t

+ U

∂T

∂x

+ U

∂T

∂x



= λ



∂

∂x

∂

∂x



+ µ



∂U

∂x





∂U

∂x





∂U

∂x





∂U

∂x



(20.21)

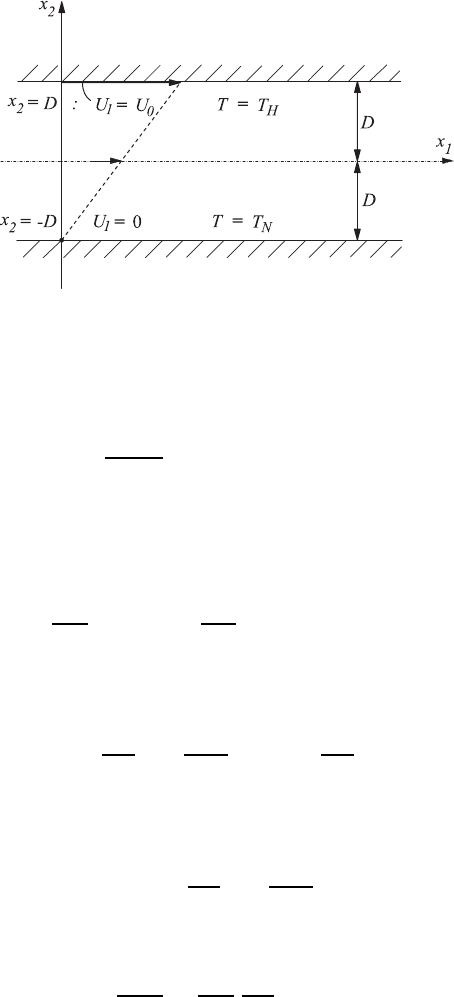
20.2 Stationary, Fully Developed Flow in Channels 631

and

Fig. 20.2 Plane ﬂow in a channel with one wall in motion and with wall temperatures

and T

Because of the assumed stationarity of the overall problem, the following

holds:

∂ (···)

∂t

= 0 for all quantities

and moreover also (∂U

/∂x

) = 0, due to the fully developed ﬂow in the x

direction and (∂T/∂x

) = 0, as the temperature ﬁeld also is assumed to be

fully developed.

With the above assumptions, one obtains from the continuity equation:

∂U

∂x

=0 ;

∂U

∂x

=0 ; U

=0. (20.22)

Equations (20.19) and (20.20) reduce for the ﬂow sketched in Fig. 20.2 to the

following forms:

0=−

∂P

∂x

+ µ

∂

∂x

;0=−

∂P

∂x

− ρg. (20.23)

From (20.23) P (x

)=−ρgx

+ Π(x

), and thus the equation for the

velocity ﬁeld can be written as:

0=−

dΠ

+ µ

. (20.24)

Standardization of this equation with x

∗

= x

/D and U

∗

= U

yields:

∗

µU

dΠ

= −A. (20.25)

For the energy equation (20.21), assuming stationarity and a fully developed

temperature ﬁeld, one obtains:

632 20 Fluid Flows with Heat Transfer

0=λ

+ µ





. (20.26)

This equation yields with T

∗

=(T − T

)/(T

− T

), with T

= the high

wall temperature and T

= the low wall temperature,

∗

= −

µU

λ (T

− T

)



∗



, (20.27)

where the normalization factor on the right-hand side represents the

Brinkmann number:

Br =

µU

λ (T

− T

)



µc





c (T

− T

)



= PrEc (20.28)

with Pr =

µc

(Prandtl number) and Ec =

c(T

− T

)

(Eckert number).

Integration of (20.25) yields

∗

= −Ax

∗

+ C

; U

= −

∗2

+ C

∗

+ C

. (20.29)

With the boundary conditions x

∗

= −1, U

∗

=0andx

∗

=1,U

∗

=1,one

obtains for the integration constants C

and C

(A + 1). Thus the

equation for the normalized velocity distribution reads

∗

(1 + x

∗

1 − x

∗2

. (20.30)

This equation expresses that the resulting velocity distribution is composed of

the Couette ﬂow

(1+x

∗

)movedbyU

and the pressure-driven Poiseuille ﬂow

A(1−x

∗2

). The linear diﬀerential equation (20.25) leads to the superposition

of the Couette and Poiseuille ﬂows.

In order to obtain the solution of the normalized temperature equation,

one ﬁrst computes the velocity gradient:

∗

− Ax

∗

. (20.31)

With (20.27), one obtains the following diﬀerential equation for the

temperature distribution:

∗

= −Br



− Ax

∗

+ A

∗2



. (20.32)

On integrating this equation, one can derive

∗

= −Br



∗2

−

∗3

∗4



+ C

∗

+ C

. (20.33)

20.3 Natural Convection Flow 633

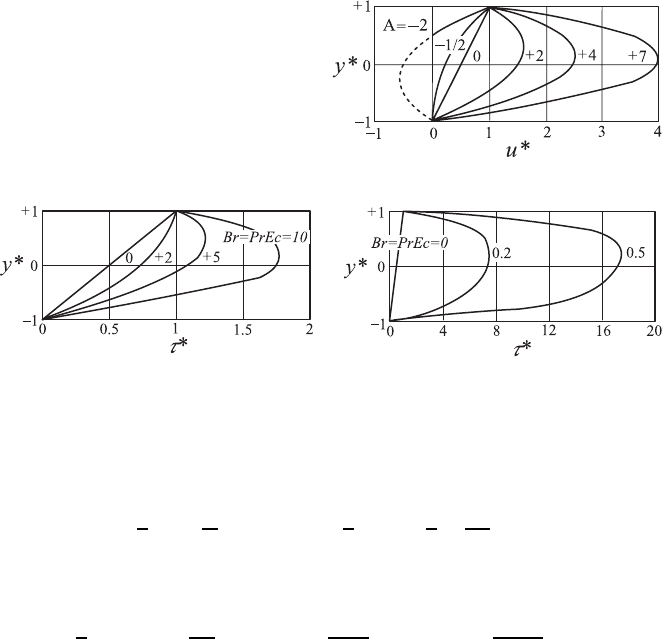
Fig. 20.3 Velocity proﬁles for diﬀerent

values of A

Fig. 20.4 Temperature proﬁles for diﬀerent Brinkmann numbers

With the boundary conditions x

∗

= −1, T

∗

=0andx

∗

=1,T

∗

=1,onecan

derive for the integration constants C

and C

− Br

and C

+ Br





. (20.34)

Equations (20.34) inserted in (20.33) yield, after rearranging the terms,

∗

(1 + x

∗

1 − x

∗2

−

BrA

∗

− x

∗3

−

BrA

1 − x

∗4

(20.35)

The resulting temperature distribution shows a ﬁrst term corresponding to

the pure heat conduction, i.e. a linear change of the temperature from T

at the lower non-moving wall to T

at the upper moving wall. The second

term results from the dissipative heat due to the linear velocity proﬁle of the

Couette ﬂow and the remaining terms from the dissipation shear of the ﬂow,

which results from the parabolic velocity proﬁle of the Poiseuille ﬂow.

The velocity and temperature proﬁles that followed from the above deriva-

tions are shown in Figs. 20.3 and 20.4 for diﬀerent parameters A and Br.

20.3 Natural Convection Flow Between Vertical Plane

Plates

In the preceding sections, ﬂows were considered for which it was assumed

that the ﬂuid properties, such as the density ρ, the dynamic viscosity µ and

the heat conduction λ, are constant. They could therefore be considered as