Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

594 19 Numerical Solutions of the Basic Equations

Fig. 19.5 Examples of structured and unstructured numerical grids

pattern in the entire solution region. Thus, for structured grids, it is generally

only necessary to store the coordinates of the grid points, as the information

on the relationship of a grid point to its neighbors, which is required for the

discretization method, is determined by the structure of the grid. In the case

of unstructured grids, such ﬁrm relationships of neighboring grid points do

not exist but have to be stored for each grid point individually.

Figure 19.5 makes clear the diﬀerence between structured, (a), and un-

structured, (b), numerical grids. It can easily be seen that for unstructured

grids there is no regularity in the order of a grid point relative to its neighbor-

ing points. Without detailed explanations, it becomes clear that the missing

structure in the grid order provides high ﬂexibility for arranging the grid

points over the entire solution regions such, that in areas with a high demand

for grid points many points can be placed. In particular, it is easily possible

with unstructured grids to capture corners and edges of ﬂow geometry such,

that they are suﬃciently resolved for supplying a good numerical solution of a

ﬂow problem. However, a considerable disadvantage is that unstructured grids

require high computer storage core spaces. Besides the grid points themselves,

i.e. their position in the ﬂow region, neighborhood relationships between the

grid points have to be stored via index ﬁelds.

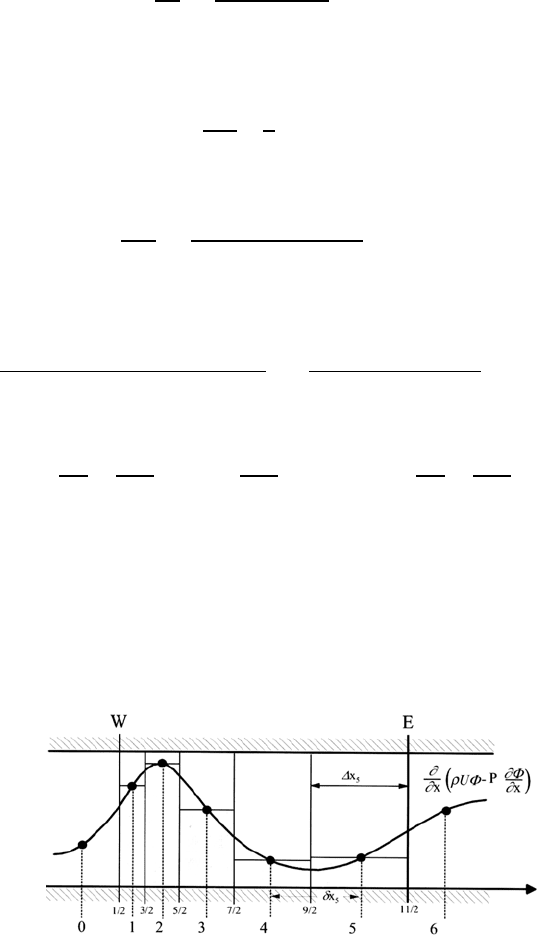
With the example of the one-dimensional stationary convection-diﬀusion

equation without sources, it will be demonstrated which advantage ﬁnite-

volume methods have in this respect, e.g. as against ﬁnite-diﬀerence methods:



ρUΦ − Γ

dΦ



=0. (19.12)

The term ρUΦ represents the convective share of the ﬂux density of Φ and

−Γ

dΦ

the diﬀusive share. This equation will now be integrated via a random

19.3 Discretization by Finite Diﬀerences 595

volume in terms of space which extends in the x direction from W to E For

the considered one-dimensional case, integration over a ﬁnite volume thus

yields



ρUΦ − Γ

dΦ



dx · 1 · 1 = 0 (19.13)

or, when carrying out the integration:



ρUΦ − Γ

dΦ





ρUΦ − Γ

dΦ



. (19.14)

In words, this means that the entire ﬂux of the quantity Φ, which at point

W ﬂows into the volume, has to ﬂow out of the volume at point E,as

no sources are present in (19.12). This shows that ﬁnite-volume methods

allow conservative, discrete formulations of the integrations of the diﬀerential

equations.

19.3 Discretization by Finite Diﬀerences

After having explained brieﬂy the discretization of the ﬂow region in

Sect. 19.2, the discretization of the general transport equation (19.11) has

to be explained. One possibility of such a discretization is given by the ﬁnite-

diﬀerence method, which, for the time being, will be explained for the case of

the one-dimensional, stationary convection-diﬀusion equation without source

terms, i.e. for the equation



ρUΦ − Γ

dΦ



=0. (19.15)

Starting from a grid point β, Φ(x + ∆x) can be represented via Taylor series

expansion as follows:

β+1

= Φ



dΦ



∆x

β+1





∆x

β+1

± 0

∆x

β+1

. (19.16)

In the same way, Φ

β−1

can be stated:

β−1

= Φ

−



dΦ



∆x

β−1





∆x

β−1

± 0

∆x

β−1

. (19.17)

By subtraction of (19.17) from (19.16), one obtains

β+1

− Φ

β−1



dΦ



(∆x

β+1

+ ∆x

β−1

)

−





∆x

β+1

− ∆x

β−1

+ ···

596 19 Numerical Solutions of the Basic Equations

For grids having equal distances between the grid points, the second term

on the right-hand side is equal to zero, so that for ∆x

β+1

= ∆x

= ∆x the

following expression holds:

dΦ

β+1

− Φ

β−1

2∆x

+ O

∆x

. (19.18)

For the terms with second derivatives one obtains by addition of (19.17) and

(19.16)

β+1

+ Φ

β−1

=2Φ





∆x

β+1

+ ∆x

β−1

+ O

∆x

(19.19)

so that for ∆x

β+1

= ∆x

β−1

= ∆x the following expression holds again:

β+1

− 2Φ

+ Φ

β−1

∆x

+ O

∆x

. (19.20)

Thus, the diﬀerential equation (19.15) for Γ = constant can be stated as a

ﬁnite diﬀerence equation as follows:

(ρU)

β+1

− (ρU )

β−1

∆x

− Γ

β+1

− 2Φ

+ Φ

β−1

∆x

=0. (19.21)

Ordered according to the unknowns Φ

β+1

, Φ

and Φ

β−1

,oneobtains:



(ρU)

β+1

∆x

−

∆x



β+1

2Γ

∆x



(ρU)

β−1

∆x

−

∆x



β−1

=0.

(19.22)

Hence, a linear system of equations results for the unknown Φ

, which has

to be solved to obtain, at each point of the numerical grid, a solution for

all variables Φ of the considered ﬂow ﬁeld. In this way, a solution path has

been found for the quantities Φ describing a ﬂow. On considering now the

solutions for Φ

in the solution area from border W to border E, indicated

in Fig. 19.6, the integral U,whereu = U is introduced:

Fig. 19.6 One-dimensional computational area

19.3 Discretization by Finite Diﬀerences 597



ρuΦ − Γ

dΦ



dx · 1 · 1 ≈



β=1

⎡

⎣



(ρu)

β+1

− (ρu)

β−1



β+1

− x

β−1

−



β+1

dΦ

β+1

− Γ

i−1

dΦ

β−1



β+1

− x

β−1

⎤

⎦

(19.23)

can only be determined by discrete integration, which has also been included

in (19.23). On writing this equation in full for the six supporting points in

Fig. 19.6, one obtains:

((ρu)

− (ρu)

) −

dΦ

− Γ

dΦ

− x

((ρu)

− (ρu)

) −

dΦ

− Γ

dΦ

− x

((ρu)

− (ρu)

) −

dΦ

− Γ

dΦ

− x

((ρu)

− (ρu)

) −

dΦ

− Γ

dΦ

− x

((ρu)

− (ρu)

) −

dΦ

− Γ

dΦ

− x

)=0.

(19.24)

When one compares (19.23) with (19.24), one recognizes that the ﬁnite-

diﬀerence method employed for the discretization does not furnish the same

result as the integration yielding (19.23). This leads to the fact that the

chosen discretization method turns out to be non-conservative. Generally, it

can be said that discretizations by means of ﬁnite-diﬀerence methods require

special measures to produce conservative discrete formulations of the basic

equations of ﬂuid mechanics. When choosing in (19.24) ∆x

= ∆x

i+1

one obtains



(ρu)

− Γ



dΦ



+(ρu)

− Γ



dΦ







(ρu)

− Γ



dΦ



+(ρu)

− Γ



dΦ





, (19.25)

i.e. all internal ﬂuxes drop out and consequently a conservative form of the

conservation equation for the unknown discrete variables Φ

results. In this

equation, both sides represent admissible approximations of the ﬂows into and

out of the solution area. The discretized equation is thus a conservative ap-

proximation of the general transport equation and the discretization scheme

598 19 Numerical Solutions of the Basic Equations

for this case is consequently conservative. However, one recognizes that for

ﬁnite-diﬀerence methods special measures have to be taken to force the con-

servativeness. Not least, it is assumed in the derivations that the numerical

grid employed does not show a strong non-equidistance. When the latter

assumption is not fulﬁlled, the method is not conservative and, moreover,

the order of the discretization method is reduced by an order of magnitude.

It is therefore emphasized once again that ﬁnite-diﬀerence methods are not

necessarily conservative. In addition, connected with this, non-conservative

formulations yield disadvantageous reductions of the order of the accuracy of

the solution methods.

19.4 Finite-Volume Discretization

19.4.1 General Considerations

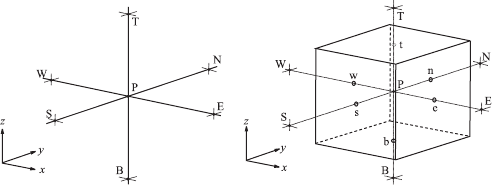
The notation used in this section is represented in Fig. 19.7. Considered is a

point P and its neighbors located in direction of the coordinate axes, e.g. of

a Cartesian coordinate system. The neighboring points in the x–y plane are

named West, South, East and North, corresponding to their position relative

to P , and the two points in the z direction are referred to as Top and Bottom

points.

For the considerations to follow, around point P a control volume is for-

mally installed, so that P is the center of this control volume. The boundary

surfaces of the control volumes are marked according to the respective neigh-

boring points, but in lower-case letters. Terms which generally would read

the same for all neighboring points, are stated with an index Nb to abbrevi-

ate the notation. Accordingly, terms for the boundary surface of the control

volume are given the index cf .

As the present considerations always start from the assumption that all

points W , S, E, N, T and B are grid points and that the grid points are

located exactly in the centers of neighboring control volumes, it is suﬃ-

cient to store only the coordinates of the control-volume boundary surfaces

Fig. 19.7 Cartesian grid and control volume with characteristic point

19.4 Finite-Volume Discretization 599

Fig. 19.8 Cross planes for explaining the basic ideas of interpolation

for numerical ﬂow computations via ﬁnite-volume methods. All other in-

formation with regard to the grid can be computed back from these data.

The distance between P and E, for example, which we denote δx

,canbe

computed as follows (see Fig. 19.8):

δx

=1/2(x

+ x

) − 1/2(x

+ x

)=1/2(x

− x

). (19.26)

In the case of non-stationary processes, a discrete representation of the

coordinate time is necessary. Discrete time planes result for the process, which

also have to be marked. Here, the style of marking is t

,ort

α+1

for each new

time level and t

α−1

for each old time level.

When, for examining the conservativeness of the formulation of discretiza-

tion, the integration of (19.15) around a point P

results in the following

relationship:

###

∆V



ρuΦ − Γ

dΦ



dV =



ρuΦ − Γ

dΦ



dx·1·1 = 0 (19.27)

and thus the integral yields



ρuΦ − Γ

∂Φ

∂x



−



ρuΦ − Γ

∂Φ

∂x



=0. (19.28)

This equation says for the individual control volume that the convective and

diﬀusive ﬂows at the East surface and the West surface are exactly the same.

The integration can thus be carried out by summing over all ﬁve control

volumes of the computation region indicated in Fig. 19.6:



β=1



ρuΦ − Γ

∂Φ

∂x



−



ρuΦ − Γ

∂Φ

∂x



=0. (19.29)

When taking into consideration that the common surface of two neighbor-

ing control volumes are identical (boundary surface e

is at the same time

600 19 Numerical Solutions of the Basic Equations

boundary surface w

β+1

), most of the ﬂuxes in the last equation cancel each

other and the following remains:



ρuΦ − Γ

∂Φ

∂x



−



ρuΦ − Γ

∂Φ

∂x



=0. (19.30)

The two surfaces which remain in the consideration are those which limit the

computational region in Fig. 19.6, i.e. W and E. Thus it holds that



ρuΦ − Γ

∂Φ

∂x



−



ρuΦ − Γ

∂Φ

∂x



=0. (19.31)

This is exactly the same equation as one would obtain by integration over the

total region; see (19.6). One recognizes that a discretization method based

on ﬁnite volumes is inherently conservative.

19.4.2 Discretization in Space

The model diﬀerential equation for a general scalar quantity Φ was stated

in Sect. 19.2. In the same section, it was shown how, by inserting diﬀerent

expressions for the individual terms of this diﬀerential equation, the basic

equations of ﬂuid mechanics can be rederived. In the present section, we

shall only consider the model equation and carry out the discretization by

means of it. The discrete forms of individual ﬂuid equations can then be

derived by inserting the expressions for Φ, Γ and S, respectively.

For the representations to be carried out here, the following transport

equation is thus considered:

∂

∂t

(ρΦ)+

∂

∂x



ρu

Φ − Γ

∂Φ

∂x



= S

. (19.32)

Here, the total ﬂux of Φ consists of the partial ﬂuxes:

ρu

Φ = convective ﬂux and −Γ

∂Φ

∂x

= diﬀuse ﬂux

and can be stated as follows:

= ρu

Φ − Γ

∂Φ

∂x

(19.33)

so that the transport equation consequently reads:

∂

∂t

(ρΦ)+

∂f

∂x

= S

. (19.34)

19.4 Finite-Volume Discretization 601

This equation is now nominally integrated over all control volumes of the

computational domain. We consider as a substitute the control volume around

a considered point P :

###

∆V

∂

∂t

(ρΦ)dV +

###

∆V

∂f

∂x

dV =

###

∆V

dV =

###

∆V

SdV (19.35)

and treat the individual expressions of this equation separately.

Applying the Gauss integral theorem, for the second term on the left-hand

side of (19.35), the following holds:

###

∆V

∂f

∂x

dV =

∆A

(19.36)

with ∆A being the surface of the control volume.

The integration over the entire control-volume surface can also be rep-

resented as the sum of the integrations over the individual boundary

surfaces:

∆A

. (19.37)

The individual external surface normals of the boundary surfaces can be

stated plainly, e.g. always are in these considerations:

⎛

⎝

−dx

⎞

⎠

and dA

⎛

⎝

⎞

⎠

. (19.38)

On introducing the scalar products f

into (19.37), one obtains:

∆A

−

∆A

−

∆A

−

∆A

. (19.39)

For the discretization, certain approximations are necessary, and they can be

taken as approximations on three diﬀerent planes. The ﬁrst approximation is

602 19 Numerical Solutions of the Basic Equations

∆A

≈ F

. (19.40)

The mean-value theorem of the integral calculus says that a value

can always be found on the surface A

so that the above relation is exactly

fulﬁlled, i.e. that:

∆A

= f

holds. To state this value a priori is not possible, however, as exactly f

quantities are supposed to be calculated. In order to state a computational

method now, the value in the center of the control-volume surface f

is used

as an approximate value of

For Cartesian geometries, it holds that ∆A

= ∆x

∆x

(j = k) and,

although A

= A

, both expressions will be used further. With analogous

approximations also for the other two directions, the following relationship

holds:

###

∆V

∂f

∂x

dV = F

− F

+ F

− F

+ F

− F

. (19.41)

The ﬁrst expression on the left-hand side of (19.35), and also the source term

of this equation, are approximated in the same way, namely by using the

value in the control-volume center as an approximation for the mean value

over the control volume:

###

∆V



∂

∂t

(ρΦ)



dV ≈

∂

∂t

(ρΦ)

∆V =

∂

∂t

(ρΦ)

∆x

(19.42)

and

###

∆V

S dV ≈ S

∆x

. (19.43)

On inserting the last three equations into (19.35), one obtains:

∂

∂t

(ρΦ)

∆V + F

− F

+ F

− F

+ F

− F

= S

∆V (19.44)

and with the expressions for the total ﬂow it results that:

∂

∂t

(ρΦ)

∆V +



ρu

Φ − Γ

∂Φ

∂x



∆A

−



ρu

Φ − Γ

∂Φ

∂x



∆A



ρu

Φ − Γ

∂Φ

∂x



∆A

−



ρu

Φ − Γ

∂Φ

∂x



∆A



ρu

Φ − Γ

∂Φ

∂x



∆A

−



ρu

Φ − Γ

∂Φ

∂x



∆A

= S

∆V. (19.45)

19.4 Finite-Volume Discretization 603

In order to increase the clarity of indexing in what follows, the variables x

and x

are replaced by x, y and z and the velocities u

, u

and u

by u,

v and w.

The next approximation step, for the derivation of a ﬁnite-volume com-

putational method, is the linearization of the expressions in question. If one

considers, e.g., the term ρuΦ, one recognizes that for Φ = u the unknown

u occurs as u

, i.e. the term is nonlinear. To be able to treat such terms,

in the computational method to be derived, in a simple way, one linearizes

them by considering the mass ﬂow density (ρu) and the diﬀusion coeﬃcient

Γ independently of the unknown quantity Φ. For computing Φ one falls back

on the values (ρu)

∗

and Γ

∗

, worked out in preceding computational steps.

Thus the values (ρu)

∗

and Γ

∗

are known for the considered computational

step, and one looks for the ﬁnal solution in several steps. The values with an

asterisk are each taken from the preceding iteration of the computations:



ρuΦ − Γ

∂Φ

∂x



≈ (ρu)

∗

− Γ

∗



∂Φ

∂x



(19.46)

and thus it follows from (19.44):

∂

∂t

(ρ

∗

)∆V +



(ρu)

∗

− Γ

∗



∂Φ

∂x





∆A

−



(ρu)

∗

− Γ

∗



∂Φ

∂x





∆A



(ρv)

∗

− Γ

∗



∂Φ

∂y





∆A

−



(ρv)

∗

− Γ

∗



∂Φ

∂y





∆A



(ρw)

∗

− Γ

∗



∂Φ

∂z





∆A

−



(ρw)

∗

− Γ

∗



∂Φ

∂z





∆A

= S

∆V.

(19.47)

In the subsequent considerations, it will be necessary again and again to

have the discrete form of the continuity equation at disposal. The continuity

equation in its general form is obtained from the equation for the general

scalar quantity by setting Φ =1,Γ =0andS = 0. With the same values,

the discrete form results from the above equation as

∂ρ

∗

∂t

∆V +(ρu)

∗

∆A

− (ρu)

∗

∆A

+(ρv)

∗

∆A

− (ρv)

∗

∆A

+(ρw)

∗

∆A

− (ρw)

∗

∆A

= 0 (19.48)

or, by abbreviating the mass ﬂuxes by m

∂ρ

∗

∂t

∆V + m

∗

− m

∗

+ m

∗

− m

∗

+ m

∗

− m

∗

=0. (19.49)

In (19.47) there are values of Φ and

∂Φ

∂x

, which have to be computed on the sur-

faces of the control volume. However, in the usually employed computational