Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.


18.7 Turbulence Models 563
Order of magnitude considerations can be carried out, employing charac-
teristic units of velocity and length scales of the considered turbulence. For
simple turbulence model considerations, ν
T
is often treated as a scalar quan-
tity, although, by definition, it constitutes a fourth-order tensorial quantity.
Strictly, by the introduction of ν
T
the assumption of isotropy of a turbulent
flow field is introduced into turbulence.
The characteristic scales of length and velocity, i.e. l
c
and u
c
,usedinthe
different models are k =
1
2
u
k
u
k
Analytical models l
c
:
∂
U
j
∂x
i
l
c
; ν
T
∼ l
2
∂
U
j
∂x
i
, (18.152)
One-equation models l
c
: k
1
2
; ν
T
∼ l
c
k
1
2
, (18.153)
Two-equation models
k
3
2
: k
1
2
; ν
T
∼
k
2
. (18.154)
“Analytical turbulence models” are characterized by describing the charac-
teristic length scale of the considered turbulence, l
c
, as a local property of
the turbulent flow field by means of an analytical relationship. This states the
distribution of the length scale as a function of the location in the flow. The
characteristic velocity is often given by the local gradient of the mean velocity
field, multiplied by the characteristic length scale of turbulence. With this the
turbulent eddy viscosity can be stated to be a product of the square of the
characteristic length scale of turbulence and the local gradient of the mean
velocity field. With the eddy viscosity introduced in this way, an additional
equation results, expressing ν
T
,whichcanbeemployedforthesolutionoftur-
bulent flow problems. However, as a new unknown the characteristic length
scale of turbulence is added, which has to be given as a function of the loca-
tion, i.e. it has to be determined from experiments and introduced into the
analytical equations for ν
T
.
The one-equation turbulence models, indicated in Fig. 18.15, maintain the
analytical description of the turbulent length scale, but solve a transport
equation for the turbulent kinetic energy k. The eddy viscosity, appearing in
the Boussinesq assumption (18.149) for the correlation −
u
i
u
j
,canthusbe
defined as a quantity which is computed from the product of the analytically
described length scale of turbulence, l
c
,andthe(k)
1
2
value calculated with the
help of a transport equation. In the transport equation for k, the occurring
correlations of turbulent property fluctuations of higher order (see (18.145)),
which were introduced by averaging the equations, are replaced by suitable
modeling assumptions.
Two-equation turbulence models represent extensions with respect to
lower equation models, where the locally existing length scale of turbulence,
i.e. l
c
, is defined with the help of the turbulent dissipation, , and this latter
property of turbulence is computed from a transport equation. When this
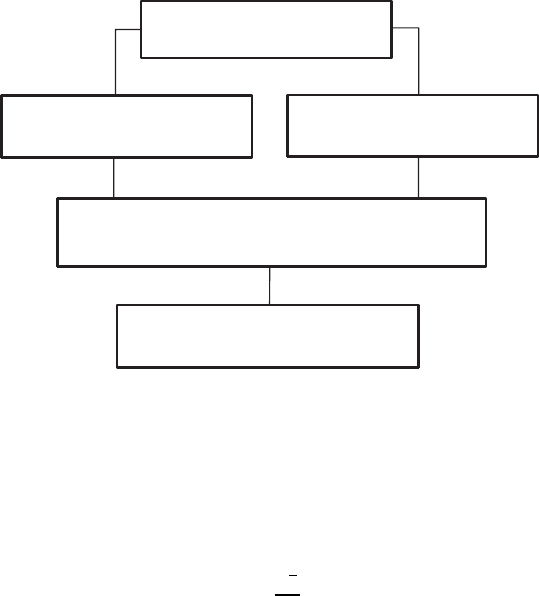
564 18 Turbulent Flows
Eddy viscosity models
Analytical equation
for eddy viscosity
One equation models
( Analytical equation for
l
c
and diff.equ. for
k
)
Two equation models
( Diff. equation for
k
&
l
c
)
Analytical equation
for mixing length
Fig. 18.15 Classification of eddy viscosity models for turbulent flows
quantity is computed locally by solving a separate transport equation, it can
be combined with the locally determined turbulent kinetic energy, k,toa
length scale of turbulence, so that the following holds:
l
c
=
k
3
2
. (18.155)
Experience with the employment of turbulence models in practice has
shown that two-equation models are at least necessary to obtain mathemat-
ical formulations of turbulence model equations that have a certain general
validity. As shown in Sect. 18.7.5, the model constants appearing in the
transport equations for k and , can be determined from direct numerical
computations, or from experimental studies of basic flows, and can later be
applied to a wide range of practically relevant flows. In this way, solutions for
the mean flow field and the most important turbulence quantities result and
the computed quantities agree with experimental data with a precision suffi-
cient for practical application. Employing analytical models of turbulence, or
one-equation turbulence models, does not lead to the same generally valid ap-
plicability of once determined constants appearing in the transport equations.
Similarly, in lower order models the analytical expressions far the turbulent
velocity and length scale are far less generally applicable. For the analytical
turbulence models and the one-equation turbulence models, it is important
to find, for each flow geometry, new turbulence information for the model
quantities and to formulate them in appropriate equations. Hence specific
turbulence models result.
18.7 Turbulence Models 565
A further generalization of the applicability of turbulence models for the
Reynolds differential equations was reached by the development of the so-
called Reynolds stress turbulence models. These models do not use eddy
viscosity formulations for the turbulent transport quantities, but solve a
transport equation for each of the cited
u
i
u
j
terms. These transport equa-
tions for the
u
i
u
j
terms can be derived from the Navier–Stokes equations;
however, they lead to correlation terms of higher order, for which also model-
ing assumptions have to be introduced. Experience seems to show that these
model assumptions for higher-order terms can be found more easily in a gen-
erally valid form than transport assumptions for correlations of lower order.
This is one of the main reasons for the generally wide employment of the
Reynolds stress turbulence models. In comparison with two-equation turbu-
lence models, they show an increased number of partial differential equations
which have to be solved. The availability of increased computing capacity
and increasing computing performance, already makes this kind of turbulence
modeling appear interesting for practical computations.
Although the above-cited turbulence models use essentially local quantities
for determining turbulent transport quantities, the solutions of the differential
equations describing the turbulence properties include also global information
on the entire flow field. This takes into account that the computed turbulence
quantities comprise the effect of an entire spectrum of quantities, and thus
also those from eddy sizes of the order of magnitude of the entire flow field.
The transport equations solved, e.g for k and , take into account also the val-
ues of their corresponding quantities existing at the boundaries of the flows.
Local transport processes enter into the computations also. Nevertheless, the
cited turbulence models give grounds for discussion as to whether they include
sufficiently all essential properties of turbulence and their effects on the un-
known
u
i
u
j
correlations. It can be hoped, however, that open questions will be
solved by detailed experimental investigations, such as are possible nowadays
with modern methods of flow measurements, as laser Doppler anemometry
and hot wire anemometry.
18.7.3 Zero-Equation Eddy Viscosity Models
In the preceding section, the introduction of a turbulent eddy viscosity, as
suggested by Boussinesq, was explained briefly as a quantity only charac-
terizing sufficiently isotropic turbulence. The postulated analogy between
the molecule-dependent momentum transport and turbulence-dependent
momentum transport led to the following ansatz:
(τ
turb
)
ij
= ρu
i
u
j
= −ρν
T
∂
U
j
∂x
i
+
∂
U
i
∂x
j
(18.156)
which, for plane-parallel flows, is reduced to a single term (e.g. x
1
=flow
direction; x
2
= vertical to the flow direction and to the wall):

566 18 Turbulent Flows
ρu
2
u
1
= ρν
T
∂U
1
∂x
2
. (18.157)
For the determination of ν
T
, Prandtl made use of simple considerations taken
from the kinetic gas theory. This theory was developed by Boltzmann and
used for the derivation of the molecule-dependent momentum transport, i.e.
for the introduction of fluid viscosity. By introducing so-called turbulent ed-
dies, it is possible, following Prandtl’s suggestion, to postulate “a uniform
size for the moment transporting eddies” of a turbulent flow field. These
turbulent eddies perform stochastic motions in space. They are assumed to
cover a path length l
m
, the so-called turbulent mixing length, before they in-
teract with other turbulent eddies, exchanging their momentum. This means
that the actually occurring continuous interaction between turbulent flow
sub-domains is modeled by a process, where the interaction of turbulence
eddies is postulated to take place only after passing a finite distance. The ex-
tent to which this simplified model process can derive properly the actually
occurring turbulent transport processes, has to be demonstrated by compar-
isons of theoretically derived insights into turbulent transport processes with
corresponding experimental results.
Taking into account the above model explanations, a turbulent field can be
subdivided into turbulent eddies in such a way that there are n
T
eddies per
unit volume. They carry out stochastic motions, so that (1/6n
T
)ofthetur-
bulent eddies move, on average, in each of the positive and negative directions
of a Cartesian coordinate system. During a time ∆t the below-cited number
of turbulence eddies is moving through the area a
2
of a control volume, where
|u
2
| was assumed to be the velocity of the eddies in the x
2
-direction, i.e. in
the consideration carried out here, u
c
= |u
2
| is set.
1
6
n
T
a
2
|u
2
|∆t =
1
6
n
T
a
2
u
c
∆t. (18.158)
On attributing to each turbulent eddy the mass ∆m
T
, then for the mass
transported through an area a
2
in a time ∆t in the positive and negative
x
2
-direction, the following relationship holds:
1
6
n
T
∆m
T
a
2
u
c
∆t =
ρ
6
a
2
u
c
∆t. (18.159)
Connected with this mass transport is the momentum transport. The
transport occurring in the positive direction can be given as
J
+
=
ρ
6
a
2
u
c
∆tU
1
(x
2
− l
m
) (18.160)
and in the negative direction
J
−
= −
ρ
6
a
2
u
c
∆tU
1
(x
2
+ l
m
). (18.161)

18.7 Turbulence Models 567
The momentum transport difference which occurs over an area a
2
in a time
∆t therefore is:
∆J = J
+
+ J
−
=
ρ
6
a
2
u
c
∆t
7
U
1
(x
2
− l
m
) − U
1
(x
2
+ l
m
)
8
. (18.162)
Per unit time and unit area this results in the following relationships:
∆J
a
2
∆t
=(τ
turb
)
21
=
ρ
6
u
c
7
U
1
(x
2
− l
m
) − U
1
(x
2
+ l
m
)
8
. (18.163)
After carrying out Taylor series expansion for the velocity difference U
1
(x
2
−
l
m
)andU
2
(x
2
+ l
m
) and subtraction, one obtains
(τ
turb
)
21
=
ρ
6
u
c
−2
∂
U
1
∂x
2
l
m
(18.164)
or rewritten:
(τ
turb
)
21
= −
ρ
3
u
c
l
m
∂
U
1
∂x
2
. (18.165)
Taking into account that the contribution occurring due to |u
2
| is given by
the term:
|u
2
| =
∂
U
1
∂x
2
l
m
= u
c
(18.166)
the following expression holds:
(τ
turb
)
21
= −ρu
2
u
1
= −
ρ
3
l
2
m
∂
U
1
∂x
2
∂
U
1
∂x
2
. (18.167)
On introducing the Prandtl mixing length as:
l
2
p
=
1
3
l
2
m
(18.168)
one obtains the final relationship put forward by Prandtl for the turbulent
momentum transport:
(τ
turb
)
21
= −ρl
2
p
∂
U
1
∂x
2
∂
U
1
∂x
2
(18.169)
and thus the turbulent viscosity can be expressed as:
ν
T
= l
2
p
∂
U
1
∂x
2
. (18.170)
Corresponding to the representations in Sect. 18.7.2, for the Prandtl
mixing length model, the following time and velocity scales of turbulence
result:
568 18 Turbulent Flows
l
c
= l
p
,u
c
= l
p
∂
U
1
∂x
2
. (18.171)
In the treatment of turbulence, l
p
has to be considered as an unknown quan-
tity in the above derivations. It has to be given analytically as a local quantity
for each turbulent flow field to be investigated, before solutions of the basic
equations for turbulent flows can be sought. To make this clearer, the turbu-
lent channel flow, for which the following basic equations hold, will be treated
below as an example.
Continuity equation:
∂
U
2
∂x
2
=0 ;
U
2
= constant = 0. (18.172)
Reynolds equations:
0=−
∂
¯
P
∂x
1
+
∂
∂x
2
ρν
d
U
1
dx
2
− ρu
2
u
1
, (18.173)
0=−
∂
¯
P
∂x
2
+
d
dx
2
−ρ
u
2
2
(18.174)
and the boundary conditions:
x
2
= ±D : U
1
=0; u
2
2
=0; ρu
2
u
1
=0
and P (x
1
,x
2
)=P
w
(x
1
) (18.175)
x
2
= 0 symmetry conditions
∂
∂x
2
(···)=0. (18.176)
The integration of the second Reynolds equation yields:
P (x
1
,x
2
)=P
w
(x
1
) − ρu
2
2
. (18.177)
From the second Reynolds equation, the following results, therefore, for
the pressure gradient in the flow direction:
∂P
∂x
1
=
dP
w
dx
1
. (18.178)
Because of the assumption of a fully developed flow field, also with regard to
the turbulent quantities, the following relationship holds:
∂
∂x
1
−ρ
u
2
2
=0. (18.179)
This relationship expresses that the change in pressure in the flow direction,
that occurs in the entire flow field, is equal to the pressure gradient along
the wall.
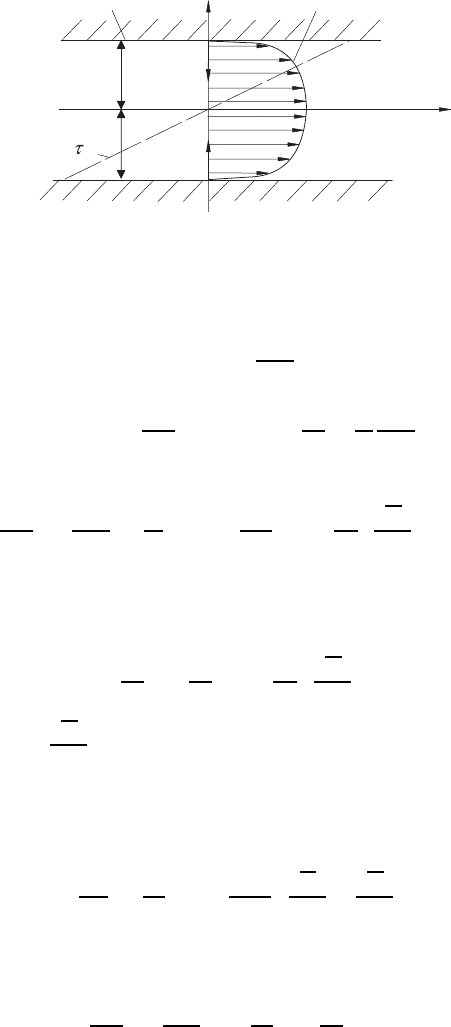
18.7 Turbulence Models 569
x
x
Turbulent velocity profile
Channel wall
1
2
ges
-y
y
D
D
Fig. 18.16 Turbulent fully developed, plane channel flow
As an integral relationship for the channel flow plotted in Fig. 18.16, one
can write:
2τ
w
BL = L
dP
w
dx
1
2DB (18.180)
or
τ
w
= D
∂P
∂x
1
; u
2
τ
=
τ
w
ρ
=
D
ρ
dP
w
dx
1
. (18.181)
The first of the Reynolds equations can thus be written as follows:
∂P
∂x
1
=
dP
w
dx
1
=
ρ
D
u
2
τ
= ρν
d
dx
2
1+
ν
T
ν
d
U
1
dx
2
(18.182)
or expressed by the wall coordinate y:
y = D −x
2
and dy = −dx
2
, (18.183)
u
2
τ
D
= ν
d
dy
1+
ν
T
ν
d
U
1
dy
. (18.184)
With ν
T
= l
2
P
d
U
1
dy
and the linear ansatz suggested by Prandtl:
l
P
= κy (18.185)
the following differential equation results:
u
2
τ
νD
=
d
dy
1+
κ
2
y
2
ν
d
U
1
dy
d
U
1
dy
. (18.186)
To solve the above equations, it is recommended to carry out the first
integration for the momentum equation in the following form:
∂P
∂x
1
=
dP
w
dx
1
= −
τ
w
D
= −
d
dy
(τ
tot
)
21
(18.187)

570 18 Turbulent Flows
and
(τ
tot
)
21
=
τ
w
D
y + C = −τ
w
1 −
y
D
, (18.188)
where y = D −x
2
was considered. Thus the following equation holds:
−ρν
d
U
1
dy
+ ρ
u
2
u
1
= −τ
w
1 −
y
D
, (18.189)
ρν
d
U
1
dy
− ρν
T
dU
1
dy
= τ
w
1 −
y
D
. (18.190)
On setting U
+
1
=
U
1
u
τ
and y
+
=
yu
τ
ν
,oneobtains:
1 −
ν
T
ν
dracU
+
1
y
+
=
1 −
y
+
D
+
(18.191)
and with
ν
T
ν
=
l
2
P
ν
dU
1
dy
=
!
l
+
P
"
2
dU
+
1
dy
+
, (18.192)
1+
!
l
+
P
"
2
dU
+
1
dy
+
dU
+
1
dy
+
=
1 −
y
+
D
+
. (18.193)
On introducing the linear relation suggested by Prandtl:
l
+
P
= κy
+
(18.194)
one obtains:
1+κ
2
y
+2
dU
+
1
dy
+
dU
+
1
dy
+
=
1 −
y
+
D
+
. (18.195)
For the upper half-plane of the channel flow
dU
+
1
dy
+
=
dU
+
1
dy
+
. The following
equation thus holds:
U
+
1
y
+
2
+
1
κ
2
y
+2
U
+
1
y
+
−
1
κ
2
y
+2
1 −
y
+
D
+
= 0 (18.196)
or solved for
dU
+
1
dy
+
it results (for
dU
+
1
dy
+
> 0):
dU
+
1
dy
+
= −
1
2κ
2
y
+2
+
9
:
:
:
:
;
1+4κ
2
y
+2
1 −
y
+
D
+
4κ
4
y
+4
A
(18.197)

18.7 Turbulence Models 571
or rewritten:
U
+
1
y
+
=
−
1
2κ
2
y
2
+
√
A
1
2κ
2
y
2
+
√
A
1
2κ
2
y
2
+
√
A
(18.198)
to yield the following result:
U
+
1
y
+
=
2
1 −
y
+
D
+
1+
0
1+4κ
2
y
+2
1 −
y
+
D
+
(18.199)
so that U
+
1
can be computed as follows:
U
+
1
=
y
+
#
0
2
1 −
y
+
D
+
1+
$
1+4κ
2
y
+2
1 −
y
+
D
+
dy
+
. (18.200)
Detailed considerations of the turbulence behavior near walls indicated that
the attenuation of the turbulence taking place near walls is not fully taken
into account by the linear assumptions for l
p
proposed by Prandtl. Through
considerations of the Stokes problem of a viscous flow oscillating parallel to a
fixed wall, van Driest derived an attenuation factor which can be introduced
into the assumptions for the Prandl mixing length. Considering this leads to
the equation
l
vD
= l
P
3
1 − exp
*
−
y
U
τ
ν
A
+
+4
, (18.201)
where A
+
= 26 was determined by van Driest from experimental results.
For large values of y
+
, the above attenuation factor approaches the value
1 and the van Driest mixing length theory and the Prandtl assumptions
merge, i.e. become identical. Near the wall, owing to the viscous attenuation,
a reduction of the mixing length takes place, which is taken into account in
the exponential term of the van Driest assumption.
Finally, some considerations on the Prandtl mixing length theory and
the derived final relationships for the turbulent momentum transport are
recommended:
−
u
1
u
2
= −l
P
u
c
∂U
1
∂x
2
= −u
2
c
l
P
u
c
∂
U
1
∂x
2
. (18.202)
On introducing two time scales:
Characteristic time scale of the turbulence: τ
c
=
l
P
u
c
,
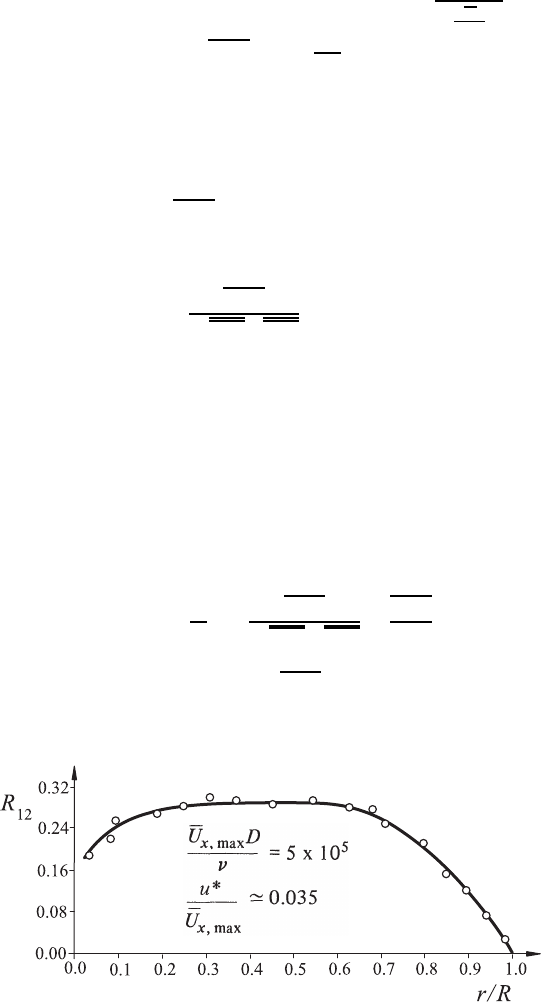
572 18 Turbulent Flows
Characteristic time scale of the mean flow field: τ
M
=
1
∂U
1
∂x
2
the follow-
ing holds:
−
u
1
u
2
= −u
2
c
τ
c
τ
M
. (18.203)
For turbulent flows for which the turbulence is exposed for a long time to
a mean flow field with constant deformation, a constant relationship of the
above time scale develops, so that, at least in some regions of the flow, the
following can be assumed to hold:
u
1
u
2
= constant · u
2
c
. (18.204)
For this reason, and for a wide range of such turbulent flows, one can write
R
12
=
u
1
u
2
u
2
1
u
2
2
= constant. (18.205)
In spite of the fact that a constant deformation rate in turbulent wall bound-
ary layers is not guaranteed and that therefore turbulence elements experience
differing deformations on their way through the flow field, the above relation-
ship also holds over wide ranges of turbulent boundary layers. This is indicted
in Fig. 18.17.
When turbulent modeling is desired only for one class of flows, e.g. tur-
bulent wall boundary layers, R
12
can also be stated from experiments as
a function of the location. For the experimentally obtained distribution in
Fig. 18.17, one can derive
R
12
= f
r
R
=
u
1
u
2
u
2
1
u
2
2
≈
u
1
u
2
k
. (18.206)
Knowing k,viaR
12
the local value for u
1
u
2
can be computed and employed
in the momentum equation for computing the mean flow field.
Fig. 18.17 Correlation coefficient R
12
for turbulent pipe flows
