Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.

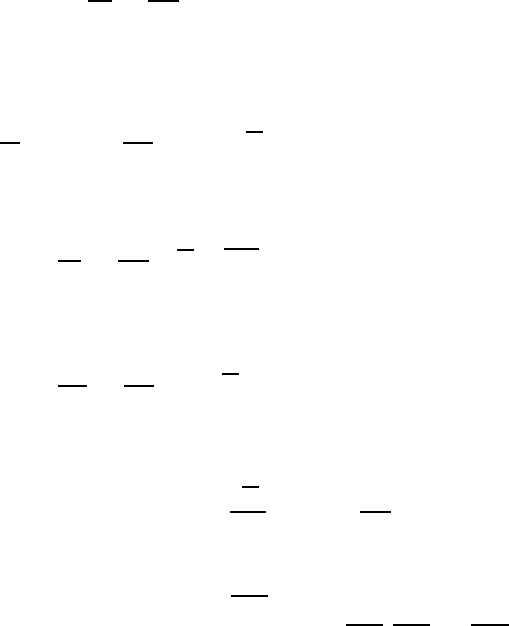
18.5 Time-Averaged Basic Equations of Turbulent Flows 543
18.5.1 The Continuity Equation
In Chap. 5, the continuity equation was derived as a mass-conservation equa-
tion which holds in the following form for the instantaneous values of the
density and the velocity components:
∂ ˆρ
∂t
+
∂
∂x
i
ˆρ
ˆ
U
i
=0. (18.74)
By introducing for the instantaneous values the time mean values and the
corresponding turbulent fluctuations, the continuity equation can also be
written as follows:
∂
∂t
(¯ρ + ρ
)+
∂
∂x
i
7
(¯ρ + ρ
)
!
U
i
+ u
i
"8
=0. (18.75)
By time-averaging this equation, one obtains, applying the time-averaging
rules indicated in Sect. 18.3.1:
∂ ¯ρ
∂t
+
∂
∂x
i
¯ρ
U
i
+ ρ
u
i
=0. (18.76)
This time-averaged equation can now be subtracted from (18.75), so that one
obtains for the instantaneous density changes:
∂ρ
∂t
+
∂
∂x
i
!
¯ρu
i
+ U
i
ρ
"
=0. (18.77)
For fluids with constant density, the above equations can be written in a
simplified way:
¯ρ =ˆρ = constant and thus ρ
=0 ⇒
∂
U
i
∂x
i
=0and
∂u
i
∂x
i
=0. (18.78)
These two final equations can now be employed for dealing with turbulent
fluid flows. In connection with this, it has to be taken into consideration
that the covariance between ρ
and u
j
, i.e. ρ
u
j
appearing in the continuity
equation for the mean values, represents three unknowns,
ρ
u
1
, ρ
u
2
and ρ
u
3
,
which have to be considered when solving fluid flow problems with variable
density. These quantities represent turbulence-dependent mean mass flows in
the x
1
-, x
2
-andx
3
-directions, which appear superimposed on the mass flows
due to the mean flow field. It is interesting to see from equations for fluids
with constant density that time averaging of the continuity equation does
not result in an additional unknown, i.e.
• For fluids of constant density, the time-averaging of the continuity equation
does not result in additional turbulent transport terms. Through the con-
tinuity equation no “additional unknowns” are introduced for fluids with
constant density, when dealing theoretically with turbulent flows, using
the time-averaged continuity equation.
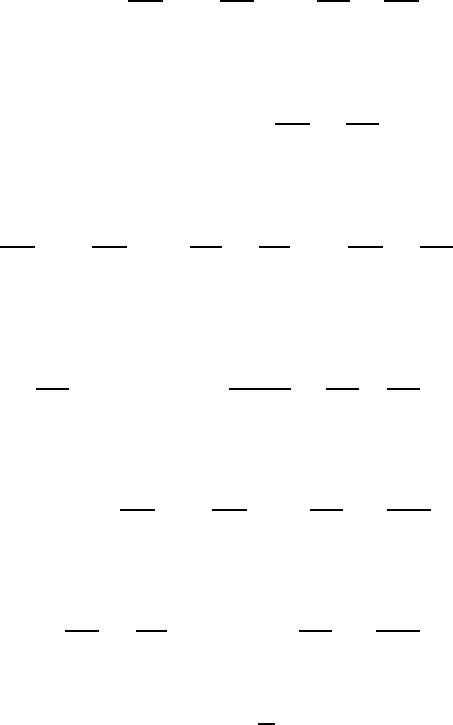
544 18 Turbulent Flows
This advantage of fluids with constant density, set forth in the above point,
when dealing theoretically with turbulent flows, is the reason for the restric-
tions imposed in the subsequent sections. This means that all derivations
from here onwards are carried out for fluids with constant density.
18.5.2 The Reynolds Equation
In Chap. 5, the equation of momentum was stated in the following form:
ˆρ
3
∂
ˆ
U
j
∂t
+
ˆ
U
i
∂
ˆ
U
j
∂x
i
4
= −
∂
ˆ
P
∂x
j
−
∂ˆτ
ij
∂x
i
+ˆρg
j
(18.79)
and for Newtonian fluids with ˆρ = constant the ˆτ
ij
term can be expressed as:
ˆτ
ij
= −µ
*
∂
ˆ
U
j
∂x
i
+
∂
ˆ
U
i
∂x
j
+
(18.80)
so that (18.79) can be written as:
ˆρ
3
∂
ˆ
U
j
∂t
+
ˆ
U
i
∂
ˆ
U
j
∂x
i
4
= −
∂
ˆ
P
∂x
j
+
∂
∂x
i
3
µ
*
∂
ˆ
U
j
∂x
i
+
∂
ˆ
U
i
∂x
j
+4
+ˆρg
j
. (18.81)
With the continuity equation for fluids of constant density, i.e. for ˆρ =
constant:
∂
ˆ
U
i
∂x
i
=0 andthus
∂
2
ˆ
U
i
∂x
i
∂x
j
=
∂
∂x
j
*
∂
ˆ
U
i
∂x
i
+
=0. (18.82)
Hence the Navier–Stokes equations, for j =1, 2, 3, can be written as follows:
ˆρ
3
∂
ˆ
U
j
∂t
+
ˆ
U
i
∂
ˆ
U
j
∂x
i
4
= −
∂
ˆ
P
∂x
j
+ µ
∂
2
ˆ
U
j
∂x
2
i
+ˆρg
j
(18.83)
or by including the continuity equation:
ˆρ
3
∂
ˆ
U
j
∂t
+
∂
∂x
i
ˆ
U
i
ˆ
U
j
4
= −
∂
ˆ
P
∂x
j
+ µ
∂
2
ˆ
U
j
∂x
2
i
+ˆρg
j
. (18.84)
If one introduces:
ˆρ =¯ρ and ρ
=0;
ˆ
U
j
= U
j
+ u
j
also
ˆ
P =
¯
P + p
, (18.85)
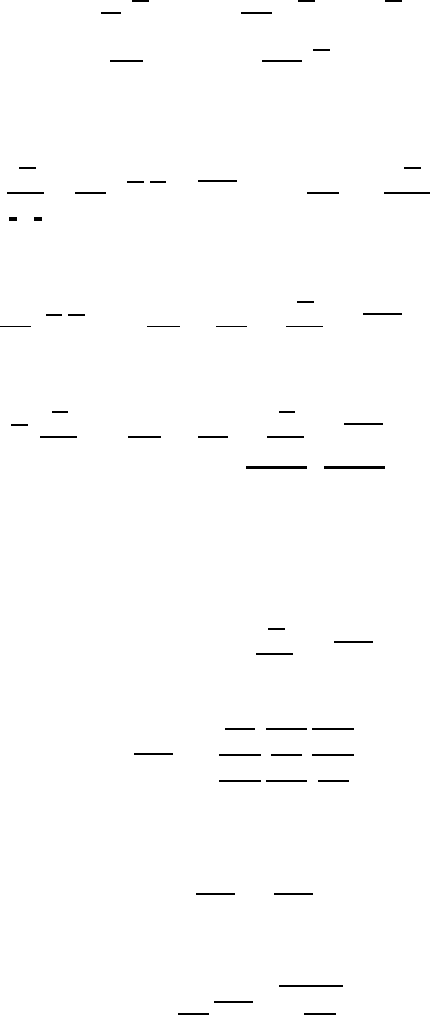
18.5 Time-Averaged Basic Equations of Turbulent Flows 545
(18.84) results in
¯ρ
∂
∂t
!
U
j
+ u
j
"
+
∂
∂x
i
7!
U
i
+ u
i
"!
U
j
+ u
j
"8
= −
∂
∂x
j
!
¯
P + p
"
+ µ
∂
2
∂x
i
2
!
U
j
+ u
j
"
+¯ρg
j
(18.86)
and after completion of time-averaging of all terms of the equation
¯ρ
⎡
⎢
⎢
⎣
∂
U
j
∂t
=0
+
∂
∂x
i
U
i
U
j
+ u
i
u
j
⎤
⎥
⎥
⎦
= −
∂
¯
P
∂x
j
+ µ
∂
2
U
j
∂x
2
i
+ g
j
. (18.87)
Rearranging the terms, one obtains
¯ρ
∂
∂x
i
!
U
i
U
j
"
= −
∂
¯
P
∂x
j
+
∂
∂x
i
µ
∂
U
j
∂x
i
− ¯ρu
i
u
j
+¯ρg
j
. (18.88)
Considering the continuity equation for fluids of constant density, one obtains
¯ρ
U
i
∂U
j
∂x
i
= −
∂
¯
P
∂x
j
+
∂
∂x
i
µ
∂
U
j
∂x
i
− ¯ρu
i
u
j
−(τ
ij
)
tot
+¯ρg
j
. (18.89)
This equation shows that, due to the time-averaging of the non-linear terms
on the left-hand side of the Navier–Stokes equations, additional terms are in-
troduced into the Reynolds equations, which can be interpreted as additional
momentum transport terms, so that for a turbulent fluid flow the following
holds:
(τ
ij
)
tot
= −µ
∂
U
j
∂x
i
+¯ρu
i
u
j
. (18.90)
The additional terms represent a tensor which can be stated as follows:
u
i
u
j
=
⎛
⎝
u
1
2
u
1
u
2
u
1
u
3
u
2
u
1
u
2
2
u
2
u
3
u
3
u
1
u
3
u
2
u
3
2
⎞
⎠
. (18.91)
This tensor is called in the literature the Reynolds “stress tensor.” It is
diagonally symmetrical, i.e. the following holds:
u
i
u
j
=
u
j
u
i
. (18.92)
Furthermore, because ˆρ =¯ρ = constant, the following relationship holds:
∂
∂x
i
u
i
u
j
= u
i
∂u
j
∂x
i
(18.93)

546 18 Turbulent Flows
as the u
j
∂u
i
∂x
i
term is equal to zero, because of the continuity equation, written
for the fluctuating velocity components.
The diagonal terms appearing in the Reynolds stress tensor can be in-
terpreted as “normal stresses”, whose significance for the time-averaged
transport of momentum is negligible in many fluid flows. The non-diagonal
terms, i.e. the terms
u
i
u
j
for i = j,represent,inmanyfluidflows,themain
transport terms of the momentum which are due to the turbulent velocity
fluctuations. This makes it clear that the splitting of the instantaneous veloc-
ity components into a mean component and a turbulent fluctuation leads to a
division of the total momentum transport in a mean part and in a turbulent
part. The total momentum transport develops on the one hand due to the
mean flow field, ρ
U
i
U
j
, and on the other due to correlations of the turbulent
velocity fluctuations, ρ
u
i
u
j
. This subdivision is very useful for many consid-
erations in fluid mechanics of turbulent flows. It means, however, as far as the
momentum transport equations are concerned, that six additional unknown
quantities appear, namely all terms of the Reynolds stress tensor. The in-
troduction of the instantaneous values of the velocity fluctuations, and the
employed time averaging, thus results in a system of equations which is not
closed: it contains more unknowns than equations that are at disposal for the
solution of fluid-flow problems. It is nowadays one of the main tasks of turbu-
lence research to link the additional unknowns of the Reynolds stress tensor
to the components of the mean flow field in such a way that independent
additional equations result, which can be employed to solve fluid flow prob-
lems. Deriving such additional relationships is called turbulence modeling.
The main elements of turbulence modeling are summarized in Sect. 18.7.
18.5.3 Mechanical Energy Equation
for the Mean Flow Field
In the preceding section, the momentum equations for Newtonian fluids of
constant density were derived as follows:
¯ρ
U
i
∂U
j
∂x
i
= −
∂
¯
P
∂x
j
+
∂
∂x
i
µ
∂
U
j
∂x
i
− ¯ρu
i
u
j
+¯ρg
j
. (18.94)
On multiplying this equation by
U
j
,oneobtains
¯ρ
U
i
U
j
∂U
j
∂x
i
= −U
j
∂
¯
P
∂x
j
+ U
j
∂
∂x
i
µ
∂
U
j
∂x
i
− ¯ρu
i
u
j
+¯ρg
j
U
j
(18.95)
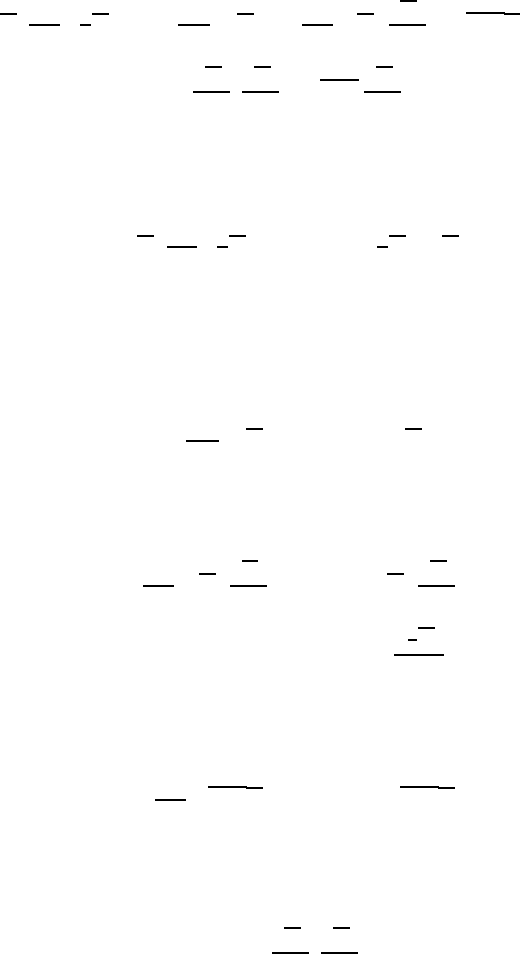
18.5 Time-Averaged Basic Equations of Turbulent Flows 547
or rearranging this equation for g
j
=0:
¯ρ
U
i
∂
∂x
i
1
2
U
2
j
= −
∂
∂x
j
!
¯
P
U
j
"
+
∂
∂x
i
µ
U
j
∂U
j
∂x
i
− ¯ρu
i
u
j
U
j
−µ
∂
U
j
∂x
i
∂U
j
∂x
i
+¯ρu
i
u
j
∂U
j
∂x
i
.
(18.96)
The different terms of the mechanical energy equation, derived for a unit
volume and a unit time and by time averaging, can now be interpreted as
follows, if the considerations are carried out for a fixed control volume:
###
δV
¯ρU
i
∂
∂x
i
1
2
U
2
j
dV =
##
δ0
1
2
U
2
j
ρ
U
i
dF
i
.
The above term represents the mean kinetic energy of the flow field flowing
in and out through the surfaces of a control volume. (As the energy equation
was derived from the momentum equation, it comprises only terms which can
be designated mechanical energy terms.)
−
###
δV
∂
∂x
j
!
¯
P
U
j
"
dV = −
##
δ0
¯
P
U
j
dF
j
.
The above term indicates what pressure energy per unit time flows in and
out of the control volume.
###
δV
∂
∂x
i
µ
U
j
∂U
j
∂x
i
dV =
##
δ0
µU
j
∂U
j
∂x
i
dF
i
=
##
δ0
µ
∂
1
2
U
2
j
∂x
i
dF
i
.
This above term indicates the molecule-caused inflow and outflow of the
kinetic energy of the fluid flow.
−
###
δV
∂
∂x
i
¯ρ
u
i
u
j
U
j
dV = −
##
δ0
¯ρu
i
u
j
U
j
dF
i
.
The term above describes the turbulence-dependent transport of the energy
resulting from u
j
and U
j
interactions.
−
###
δV
µ
∂
U
j
∂x
i
∂U
j
∂x
i
dV.
548 18 Turbulent Flows
This term indicates how the dissipation of the mean energy by viscosity
takes place.
###
δV
¯ρu
i
u
j
∂U
j
∂x
i
dV.
The last term of (18.96) describes how the energy of the mean flow field
is turned into turbulence, i.e. how turbulence is produced by the interac-
tion of turbulence with the mean flow field. (The energy withdrawn from
the mean flow field leads to the production of energy of turbulent fluid-flow
fluctuations.)
The product of the negative correlation of the turbulent velocity fluctua-
tions u
i
and u
j
and the gradient of the mean flow field yields the following
term, which is called production term of turbulence:
−¯ρ
u
i
u
j
∂U
j
∂x
i
. (18.97)
This term occurs in the differential transport equation of the turbulent kinetic
energy. Because of the symmetry of the Reynolds stress tensor, it can also be
written as follows:
−¯ρ
u
i
u
j
∂U
j
∂x
i
= −¯ρu
i
u
j
¯
D
ij
(18.98)
with
¯
D
ij
=
1
2
∂U
j
∂x
i
+
∂U
i
∂x
j
= tensor of the time-averaged deformation rate.
It appears with a positive sign on the right-hand side of the above energy
equation for the mean flow field, and this means that the energy serving
for the production of turbulent velocity fluctuations is withdrawn from the
mean flow field. The actual dissipation term in the mean flow energy equation
appears:
µ
∂
U
j
∂x
i
∂U
j
∂x
i
(18.99)
the significance of which, relative to the dissipation or production term of
turbulence, is negligible for many turbulent fluid flows. This can be assessed
by the subsequent order of magnitude considerations:
¯ρ
u
i
u
j
∂U
j
∂x
i
; ¯ρu
2
c
U
c
L
c
; ρ(Tu)
2
U
3
c
L
c
, (18.100)
µ
∂
U
j
∂x
i
∂U
j
∂x
i
; µ
U
2
c
L
2
c
, (18.101)
where
u
2
c
represents the effective value of a characteristic velocity fluctua-
tion present in the flow field, (Tu)
2
≈ u
2
c
/U
2
c
represents the square of the
corresponding turbulence intensity, U
c
being a characteristic velocity and
L
c
a characteristic dimension of the flow geometry. With this, the following
relationship holds:
18.5 Time-Averaged Basic Equations of Turbulent Flows 549
¯ρu
i
u
j
∂
U
j
∂x
i
µ
∂U
j
∂x
i
∂U
j
∂x
i
;
¯ρ(Tu)
2
U
3
c
L
2
c
L
c
µU
2
c
=
U
c
L
c
ν
(Tu)
2
= Re(Tu)
2
. (18.102)
As turbulence always occurs for large Reynolds numbers, e.g. Re =10
4
,
(18.102) shows that even for Tu = 20%, a comparatively large degree of
turbulence, the viscous dissipation is negligible compared with the turbulence
production. Similar considerations also hold for the terms
¯ρ
u
i
u
j
U
j
µU
j
∂
U
j
∂x
i
;
ρ
U
2
c
U
3
c
L
2
c
µU
c
U
c
L
c
;
U
c
L
c
ν
(Tu)
2
= Re(Tu)
2
(18.103)
so that for many practical computations the transport equation for the
“mechanical energy” of the mean velocity field of a turbulent flow can
be written in a simplified way, as the molecule-dependent energy trans-
port and molecular dissipations terms can be neglected compared with the
turbulence-dependent production term:
¯ρ
U
i
∂
∂x
i
1
2
U
2
j
= −
∂
∂x
j
!
¯
P
U
j
"
− ¯ρ
∂
∂x
i
u
i
u
j
U
j
+¯ρ
u
i
u
j
∂U
j
∂x
i
. (18.104)
This somewhat simplified energy equation contains all terms that are impor-
tant for the mechanical energy transport occurring for the mean flow field in
the more practical, i.e. non-academic, applications of fluid mechanics.
In order to underline the significance of the energy transport equation for
the mean flow field, for the comprehension of the turbulence production, we
shall discuss the fully developed turbulent flow between two plane plates for
which (18.104) reads as follows:
0=−
∂
∂x
1
!
¯
P
U
1
"
− ¯ρ
∂
∂x
2
7
(τ
ges
)
21
U
1
8
+¯ρ
u
1
u
2
∂U
1
∂x
2
. (18.105)
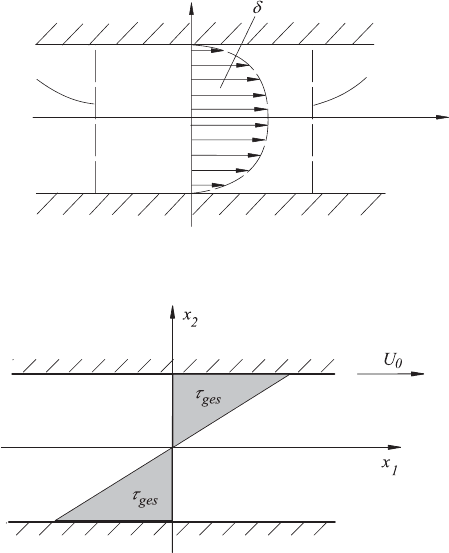
Integration over the control volume, indicated in Fig. 18.10, results in the
following relationship:
0=(P
A
− P
B
)
˙
Q −
###
δV
−¯ρ
u
1
u
2
∂U
1
∂x
2
dV. (18.106)
The entire “pressure energy” generated per unit time by a ventilator for air or
a pump for water, i.e. (P
A
−P
B
)
˙
Q, serves for the production of the turbulent
kinetic energy in the flow.
When carrying out similar considerations for the turbulent Couette flow
indicated in Fig. 18.11, the energy transport equation for this flow reads
0=−
##
δ0
(τ
ges
)
21
U
1
dF
1
−
###
δV
−¯ρ
u
1
u
2
∂U
1
∂x
2
dV. (18.107)
550 18 Turbulent Flows
x
x
V
Control plane A
1
2
Control plane B
Fig. 18.10 Plane channel flow (the employed pump energy (P
A
−P
B
)
˙
Q serves for
the production of turbulent, kinetic energy)
Fig. 18.11 Couette flow (the employed movement energy serves for the production
of turbulent, kinetic energy)
This equation expresses that the entire “driving energy” put into the plate
movement, indicated by U
0
in Fig. 18.11, is used for the production of
turbulent kinetic energy in the flow.
The above examples of turbulent flows make the significance of fluid
mechanical efforts clear to reduce the production of turbulence wherever pos-
sible, e.g. by the addition of additives to flowing fluids. By using additives
such as high molecular weight polymers or surfactants, the production of the
turbulent energy can be considerably suppressed. The achieved reduction of
turbulence production represents a considerable saving of the pump energy
which has to be introduced for the propulsion of turbulent flows.
18.5.4 Equation for the Kinetic Energy of Turbulence
In addition to the considerations of the energy balance for the mean flow field,
it is instructive for the understanding of some of the physics of turbulent flows
to consider the energy balance of the turbulent part of the flow. For this the
energy equation for the kinetic energy of turbulence is employed, which again

18.5 Time-Averaged Basic Equations of Turbulent Flows 551
is derived from the general momentum equation:
ˆρ
3
∂
ˆ
U
j
∂t
+
ˆ
U
i
∂
ˆ
U
j
∂x
i
4
= −
∂
ˆ
P
∂x
j
+ µ
∂
2
ˆ
U
j
∂x
i
2
+ˆρg
j
. (18.108)
On introducing in this equation ˆρ =¯ρ = constant and
ˆ
U
j
= U
j
+ u
j
,
ˆ
P =
¯
P + p
and neglecting g
j
,oneobtains:
ˆρ
∂
∂t
!
U
j
+ u
j
"
+
∂
∂x
i
!
U
i
+ u
i
"!
U
j
+ u
j
"
= −
∂
∂x
j
!
¯
P + p
"
+ µ
∂
2
∂x
i
2
!
U
j
+ u
j
"
. (18.109)
Multiplying this equation by (U
j
+ u
j
), the following relationship results if,
additionally, the continuity equation is taken into account:
ˆρ
∂
∂t
1
2
!
U
j
+ u
j
"
2
+
!
U
i
+ u
i
"
∂
∂x
i
1
2
!
U
j
+ u
j
"
2
= −
∂
∂x
j
7!
¯
P + p
"!
U
j
+ u
j
"8
+ µ
!
U
j
+ u
j
"
∂
2
∂x
i
2
!
U
j
+ u
j
"
(18.110)
and after time averaging the entire equation:
¯ρ
U
i
∂
∂x
i
1
2
U
2
j
+ u
2
j
+¯ρ
∂
∂x
i
U
j
u
i
u
j
+¯ρ
∂
∂x
i
u
i
u
2
j
= −
∂
∂x
j
¯
P
U
j
+ p
u
j
+
U
j
µ
∂
2
U
j
∂x
i
2
+ u
j
∂
2
u
j
∂x
i
2
. (18.111)
Subtracting the energy equation for the mean flow field:
¯ρ
U
i
∂
∂x
i
1
2
U
2
j
= −
∂
∂x
j
!
¯
P
U
j
"
+
U
j
µ
∂
2
U
j
∂x
i
2
− U
j
¯ρ
∂
∂x
i
u
i
u
j
(18.112)
one obtains as the transport equation for the turbulent kinetic energy:
¯ρ
U
i
∂
∂x
i
1
2
u
2
j
= −
∂
∂x
j
p
u
j
+
∂
∂x
j
*
µ
u
j
∂u
j
∂x
i
+
−
¯ρ
2
∂
∂x
i
u
i
u
2
j
−¯ρ
u
i
u
j
∂U
j
∂x
i
− µ
∂u
j
∂x
i
∂u
j
∂x
i
. (18.113)
The different terms of this equation can now be interpreted as follows,
showing their significance for the kinetic energy balance for a control volume:
###
δV
¯ρU
i
∂
∂x
i
1
2
u
2
j
dV =
###
δV
¯ρ
∂
∂x
i
U
i
1
2
u
2
j
dV =
##
δ0
¯ρ
2
u
2
j
U
i
dF
i
.
(18.114)
552 18 Turbulent Flows
The left-hand side term in this equation represents the turbulent kinetic
energy, transported in and out of a control volume by convection.
−
###
δV
∂
∂x
j
p
u
j
dV = −
##
δ0
p
u
j
dF
j
.
This is the pressure-velocity correlation responsible for the redistribution of
the energy of the turbulence from the j component to the other components
of the turbulent velocity fluctuations.
###
δV
∂
∂x
i
3
µ
u
j
∂u
j
∂x
i
4
dV =
##
δ0
µu
j
∂u
j
∂x
i
dF
i
=
##
δ0
µ
∂
1
2
u
2
j
∂x
i
dF
i
.
The above term describes the molecular transport of the turbulent kinetic
energy into and out of the control volume.
−
¯ρ
2
##
δV
∂
∂x
i
u
i
u
2
j
dV = −
¯ρ
2
##
δ0
u
i
u
2
j
dF
i
.
The above term is the diffusive transport of the turbulent kinetic energy by
velocity fluctuations into and out of the considered control volume.
¯ρ
###
δV
−
u
i
u
j
∂
U
j
∂x
i
dV.
This term represents the production term of the turbulent kinetic energy
which appeared in the energy equation for the mean flow field, but with
inverse sign.
−
###
δV
µ
∂u
j
∂x
i
∂u
j
∂x
i
dV.
By the above term the viscous dissipation of turbulent kinetic energy is
described, caused by the turbulent velocity fluctuations.
When defining the following total term as the “turbulent diffusion” of the
turbulent kinetic energy:
D
j
= p
u
j
− µu
i
∂u
i
∂x
j
+
¯ρ
2
u
j
u
2
i
(18.115)
the production of turbulent kinetic energy as:
P
k
= −ρu
i
u
j
∂U
j
∂x
i
(18.116)
