Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.


17.3 Generalized Instability Considerations 513
i.e. a one-dimensional stationary velocity field U
x
(y)isassumedasgiven,into
which two-dimensional time-dependent disturbances are introduced, or can
form in the flow. Furthermore, for the pressure we assume
ˆ
P = P (x)+p
(x, y, t), (17.68)
where for all fluctuation quantities we introduce:
a
A
1; i.e.
u
x
U
x
1;
u
y
U
x
1;
p
P
1. (17.69)
On introducing the quantities defined in (17.67) and (17.68) into the Navier–
Stokes equations, the following system of equations results:
∂u
x
∂x
+
∂u
y
∂y
=0, (17.70)
∂u
x
∂t
+(U
x
+ u
x
)
∂u
x
∂x
+ u
y
dU
x
dy
+
∂u
x
∂y
= −
1
ρ
dP
dx
+
∂p
∂x
+ ν
∂
2
u
x
∂x
2
+
∂
2
u
x
∂y
2
+
d
2
U
x
dy
2
, (17.71)
∂u
y
∂t
+(U
x
+ u
x
)
∂u
y
∂x
+ u
y
∂u
y
∂y
= −
1
ρ
∂p
∂y
+ ν
*
∂
2
u
y
∂x
2
+
∂
2
u
y
∂y
2
+
. (17.72)
These differential equations yield for the special case that no disturbances
exist:
0=−
1
ρ
dP
dx
+ ν
d
2
U
x
dy
2
. (17.73)
Disregarding all squared terms occurring in the disturbance quantities and
after subtraction of (17.73), one obtains the following system of equations for
the considered disturbance quantities u
x
, u
y
and p
:
∂u
x
∂x
+
∂u
y
∂y
=0, (17.74)
∂u
x
∂t
+ U
x
∂u
x
∂x
+ u
y
dU
x
dy
= −
1
ρ
∂p
∂x
+ ν
*
∂
2
u
x
∂x
2
+
∂
2
u
y
∂y
2
+
, (17.75)
∂u
y
∂t
+ U
x
∂u
y
∂x
= −
1
ρ
∂p
∂y
+ ν
*
∂
2
u
y
∂x
2
+
∂
2
u
y
∂y
2
+
. (17.76)
The introduced two-dimensionality of the disturbances allows the elimination
of the differential equation (17.74), resulting from the continuity equation,
by introducing a stream function for the velocity field of the disturbances:
u
x
=
∂Ψ
∂y
and u
y
= −
∂Ψ
∂x
. (17.77)

514 17 Unstable Flows
If one expresses (17.75) and (17.76) in this disturbance stream function Ψ
,
one obtains the following differential equations for Ψ
and p
:
∂
2
Ψ
∂y∂t
+ U
x
∂
2
Ψ
∂x∂y
−
∂Ψ
∂x
dU
x
dy
= −
1
ρ
∂p
∂x
+ ν
∂
3
Ψ
∂x
2
∂y
+
∂∂
3
Ψ
∂∂y
3
, (17.78)
−
∂Ψ
∂x∂t
− U
x
∂
2
Ψ
∂x
2
= −
1
ρ
∂p
∂y
− ν
∂
3
Ψ
∂x
3
+
∂
3
Ψ
∂x∂y
2
. (17.79)
By differentiation of (17.78) with respect to y and (17.79) with respect to x,
the terms ∂
2
p
/∂x∂y can be eliminated, so that one only obtains a differential
equation for Ψ
. The latter contains, however, terms of fourth order and can
be written as follows:
∂
∂t
+ U
x
∂
∂x
∂
2
Ψ
∂x
2
+
∂
2
Ψ
∂y
2
−
d
2
U
x
dy
2
∂Ψ
∂x
= ν
−
∂
4
Ψ
∂x
4
+2
∂
4
Ψ
∂x
2
∂y
x
−
∂
4
Ψ
∂y
4
.
(17.80)
All of the above differential equations clearly express that disturbances, as
expressed by (17.67) and (17.68), are governed by the conservation laws of
fluid mechanics and the given undisturbed flow field U
x
(y). Special solutions
can be obtained for the following ansatz for Ψ
(x, y, t):
Ψ
= f(y)exp[i (kx − ωt)] . (17.81)
Here k is always set as real, i.e. waves of wavelength λ =2π/k are considered
in the direction of the x coordinate, whose behavior are described by the
differential equation (17.80).
The quantity ω in the exponential term of the ansatz (17.81) can adopt
complex values:
ω = ω
R
+ iω
I
. (17.82)
On proving that ω
I
< 0holds,Ψ
decreases with time and the fluid flow
U
x
(y) can be regarded as stable. For ω
I
> 0, the disturbance is excited with
time, i.e. the flow U
x
(y), investigated for instabilities, proves to be unstable
with respect to the imposed disturbances.
The differential equation (17.80) is of fourth order, so that its integration
requires the implementation of four boundary conditions. They can be stated
for plane channel flows and wall boundary-layer flows as follows:
• For plane channel flow it results for y =0andy =2H that u
x
= u
y
=0,
i.e.
f(0) = f
(0) = f(2H)=f
(2H)=0. (17.83)
• For flat plate boundary layer flow one obtains, because of the no-slip
condition at the wall
f(0) = f
(0) = 0.

17.3 Generalized Instability Considerations 515
For the outer flow one can state, because of the lack of viscosity forces, i.e.
d
2
U
x
/dy
2
=0,that
f
− kf =0 ; f = ω exp(−ky). (17.84)
On setting Ψ
= f (y)exp[ik(x − ct)], the well-known Orr–Sommerfeld
differential equation results:
(kU
x
− ω)(f
− k
2
f) − kU
x
f =
ν
ik
(f
− 2k
2
f
+ k
4
f). (17.85)
This usually needs to be solved numerically for investigating the stability
of a certain flow, using the undisturbed velocity distribution U
x
(y)andthe
assumed wavelength k in the equation and employing the above-indicated
boundary conditions, e.g. for:
y =0: f(0) = f
(0) = 0,
y →∞: f (y)=f
(y) ; 0.
(17.86)
For physical considerations it is also appropriate to introduce c = ω/k =
c
R
+ic
I
. For stability considerations one therefore has to look for the solution
of an eigenvalue problem and to determine it for each wavelength of a distur-
bance, i.e. for each λ =2π/k. The wavelength range which leads to negative
values of the imaginary part of c is defined as stable, i.e. the investigated flow
is stable with respect to these disturbances. Thus, it is determined by succes-
sive computations, for which wavelength the imaginary part of c is positive.
This then leads to an insight into whether for a solution U
x
(y), that we have
for a flow, the flow field U
x
(y) changes abruptly into a flow state differing
from its undisturbed state.
When two-dimensional disturbances are imposed on considered flows, the
behavior of flows with two-dimensional velocity profiles can nowadays be
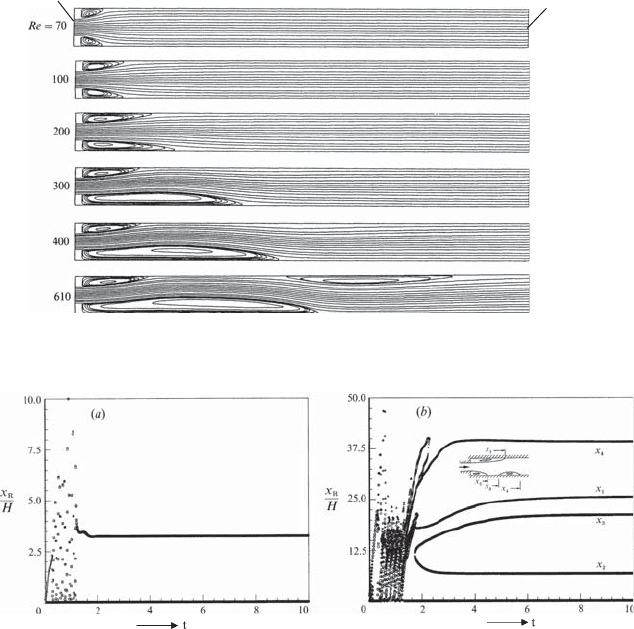
investigated numerically, e.g. plane channel flow with sudden cross-section
widening indicated in Fig. 17.11. This figure illustrates an inner flow, which
is given by a fully symmetric inflow in plane A, and shows symmetrical bound-
ary conditions between planes A and B,andinB a symmetrical profile of
the outflow exists. In spite of this, flow investigations show that the flow
profiles between planes A and B are asymmetric from a certain Re
s
value
onwards. This is stated in Fig. 17.11b, which shows that from
s
≈ 150
onwards separate regions with differing lengths and locations form.
The results in Fig. 17.11 for two-dimensional plane channel flow were
obtained numerically. For Re < Re
s
the numerical computations yielded
symmetrical velocity profiles, i.e. for this Re range the viscosity influences
were strong enough to attenuate disturbances in the flow. Thus it was pos-
sible at all locations on the symmetry axis to obtain and maintain U
2
=0
for all times. For Re > Re
s
this important condition for the symmetry of the
flow could not be fulfilled any longer, and the asymmetry of the flow indi-
cated in the lower half of Fig. 17.11 developed. This kind of investigation also
516 17 Unstable Flows
}
}
Re < Re
s
Re > Re
s
Re Re
s
~
~
a)
b)
A
B
Fig. 17.11 (a) Two-dimensional plane channel flows with sudden expansion of cross-
sectional area; (b) computation results with an asymmetry of the flow
Fig. 17.12 Computations of the separation regions for imposed disturbances for
flows of (a) Re =70and(b) Re = 610
yielded that the shorter separation region, characteristic for the asymmetry,
can occur either above or below, depending on the imposed disturbance.
When drawing the separation lengths as a function of the Reynolds num-
ber, one obtains a so-called bifurcation diagram with x
2
/x
1
= 1 for smaller
Reynolds numbers, i.e. for Re < Re
s
. This diagram would show that a bi-
furcation point S occurs for Re = Re
s
. Two branches of the characteristic
function x
2
/x
1
, typical of the asymmetry of the flow, start at Re = Re
s
.The
symmetrical solution turns out to become unstable for Re > Re
s
, i.e. the
smallest disturbances that are introduced into the flow lead to a break of
the symmetry of the flow.
In order to demonstrate that the asymmetric flow fields that develop for
Re < Re
s
are stable, the numerical solutions were exposed to considerable
disturbances in time. This is shown in Fig. 17.12, which shows (a) temporal
changes of the x
2
positions characterizing the separation region behind the
step. When the temporal disturbances are removed, the dimensions of the
17.4 Classifications of Instabilities 517
separation areas, typical for the corresponding Reynolds numbers, re-form
and take on the value of the steady-state solution. Here, the numerical com-
putations carried out showed that it is left to chance whether the shorter
separation region develops on the lower or upper wall behind the sudden
expansion. In Fig. 17.12b, several layers of separation areas appear, which
also re-establish themselves as the disturbances on the flow are removed.
17.4 Classifications of Instabilities
The complexity of the behavior of flow fluctuations, resulting from induced
disturbances due to flow instabilities, becomes clear when considering the
ansatz for the stream function for velocity fluctuations:
Ψ
(x
1
,x
2
,t)=f (x
2
)exp[i (kx
1
− ωt)] . (17.87)
On introducing k = k
R
+ ik
I
and ω = ω
R
+ iω
I
, one obtains with f(x
2
)=
F (x
2
)exp[−iθ(x
2
)]
Ψ
(x
1
,x
2
,t)=exp(ω
I
t − k
I
x
1
) {F (x
2
)cos[k
R
x
1
− ω
R
t − θ (x
2
)]}. (17.88)
If all values k
R
, k
I
, ω
R
and ω
I
are unequal to zero, a disturbance is described
by Ψ
(x
1
,x
2
,t), which is extremely complex and can only be classified as dif-
ficult to describe and even more difficult to “mentally digest.” When keeping
the space point constant for considerations within a certain range, i.e. x
1
,x
2
constant, (17.88) describes a disturbance (unstable flow) increasing with time,
or a disturbance (stable flow) decreasing with time. Here, it has to be taken
into consideration that an insight into the physics of stability or instability
of a flow is only gained for one point of the flow field. It cannot be trans-
ferred to other points. On adding other disturbances to make the complexity
of stability considerations still clearer, and if one looks at flow disturbances
for constant values of x
2
and t, increases or decreases of disturbances in the
x
1
-direction look different. One can see that direct considerations of (17.88)
lead only to a very limited extent to a deeper understanding of the stability
or instability of flows.
When the information on an existing instability for one point of the flow
field holds for the entire flow field, one talks about an absolute instability.
This occurs, e.g., when in a rotating annular flow a disturbance is introduced
which then transits from a flow free of Taylor vortices to a flow in which
Taylor vortices occur in the entire flow field.
On introducing into a flow a disturbance, which is “carried away” like,
e.g., the surface wave caused by a stone thrown into water, and when the
disturbance then increases, one talks of a convective instability. The dif-
ference to the absolute instability is indicated in Fig. 17.13. In 17.13a, the
increase of the disturbance in the entire part of the flow field with time is
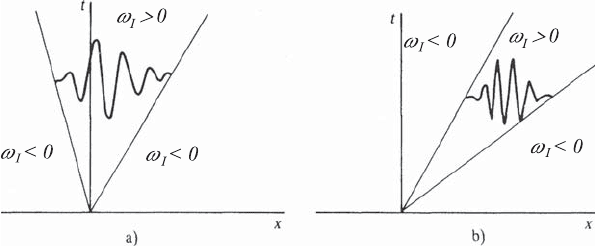
518 17 Unstable Flows
Fig. 17.13 Schematic diagrams of (a) absolute flow instability and (b) convective
instability
indicated. This is characteristic of the presence of an absolute instability of
the flow. In Fig. 17.13b, the increase of an induced disturbance with simulta-
neous movement in space is illustrated; this is characteristic of the presence
of a convective instability.
In the presence of a convective instability, “feed-back” mechanisms can
occur, such that the disturbance returns back, due to reflections, to the place
from where the disturbance started. This causes a new disturbance there,
which again is transported in a convective way and is again reflected, so that
an instability only occurs in an embedded part of the system. In this case, one
talks of a global instability. When there are global instabilities, subdivisions
with regard to the feed-back mechanisms and the interactions of the reflected
disturbances with the initial flows can be made. This is a research-active field
of modern fluid mechanics.
In the literature, further classifications of possible instabilities have been
made. We start from the following ansatz for the stream function of a
disturbance that is allowed to increase with space and time:
Ψ
(x
1
,x
2
,t)=f (x
2
)exp[i (kx
1
− ωt)] (17.89)
and considering the corresponding Orr–Sommerfeld equation:
(kU
1
− ω)
!
f
− k
2
f
"
− kU
1
f + iRe
−1
7
f
− 2k
2
f
+ k
4
f
8
=0. (17.90)
Simple stability considerations now start with the assumption that k
I
=0,
so that as the basic disturbance a sine wave serves in the x
1
-direction. For
this case, for given values of Re and k
R
, the eigenvalues of ω
R
and ω
I
are
determined. When ω
I
is positive, the amplitude of the disturbing wave grows
with time; we have a time instability of the flow. On comparing this approach
with the diagrams on the absolute flow instability in Fig. 17.13, it becomes
clear that the time analysis of flow instabilities is appropriate when one wants
to analyze a flow with regard to the presence of an absolute instability. Often
time analysis is also chosen for reasons of simplicity, even when it is evident
17.5 Transitional Boundary-Layer Flows 519
that a convective instability is involved. The reason for this can be taken
from the Orr–Sommerfeld equation (17.90). In this equation, k appears as a
factor in several terms, so that a certain simplification occurs in the solution
procedure when k is real. Strictly, one would have to set β
I
= 0 (see the text
above (17.88)), when investigating the spatial instabilities of a flow and thus
carrying out investigations for given values for Re and ω
R
to determine the
eigenvalues of k
R
and k
I
.Whenk
I
proves negative, we have an amplification
of the amplitude of the disturbance with x
1
, i.e. a spatial instability of the
flow is present. Recent investigations of flow instabilities mostly carried out
temporal and spatial analyses of the stability or instability of flows.
17.5 Transitional Boundary-Layer Flows
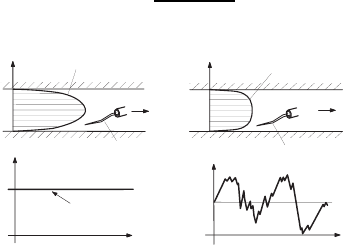
By relatively simple experimental investigations, one can detect that flows
can be in a laminar or in a turbulent flow state. Velocity sensors introduced
into a certain stationary flow lead to signals as shown in Fig. 17.14. In a flow
defined as laminar, the velocity signal shows a temporally constant velocity.
In a flow defined as being turbulent, there exists, however, a time variation
of the local velocity which shows velocity fluctuations around a mean value.
Both velocity variations with time are shown in Fig. 17.14. This makes clear
the difference in the time variations of the velocity signals. The figure also
shows the differences in the profiles of the velocity distributions.
The field of fluid mechanics that treats the transition of the laminar state
of a flow into a turbulent one, is defined as “fluid mechanics of transitional
flows.” Usually the laminar-to-turbulent transition of a flow takes place as an
intermittent process, such that a flow state is initially laminar. Introduced
flow disturbances are then excited for a short time, subsequently experiencing
an attenuation again. The flow transits initially only in an intermittent way
from the laminar into the turbulent flow state, where over the duration of
the turbulent phase, a comparison concerning the entire observation time, a
so-called “intermittent factor” can be introduced, i.e.
I
F
=
∆t
turb
T
. (17.91)
U ( )
x
2
1
U ( )
x
2
1
t
U ( , )
x
2
1
t
x
2
x
1
x
1
Laminar velocity profile
x
2
Turbulent velocity profile
Velocity sensor
Velocity sensor
Fig. 17.14 Laminar and turbulent flow states at plane channel flows
520 17 Unstable Flows
For I
F
= 0 the considered flow is, at the place of measurement, in its laminar
state and for I
F
= 1 it has reached its turbulent state. For the entire region
0 <I
F
< 1, there exists the so-called laminar-to-turbulent transitional range,
with relatively abrupt changes from the laminar to the turbulent state of
the flow. Investigations of these abrupt changes belong to the important
investigations which constitute modern fluid mechanics research. An essential
sub-domain of the current investigations in this field of research involves the
laminar-to-turbulent transition in boundary layers. The latter will be treated
here in an introductory way, with emphasis on wall boundary layers.
The basic idea of the present laminar-to-turbulent transition research
starts from the assumption that the transition from the laminar to the tur-
bulent state of a flow is concerned with the increase in disturbances. Thus,
transition research is a sub-domain of stability research carried out in fluid
mechanics. Its theory is thus based, especially where boundary-layer flows
are concerned, on the Orr–Sommerfeld equation:
(kU
1
− ω)(f
− k
2
f) − kU
1
f + iRe
−1
7
f
− 2k
2
f
+ k
4
f
8
=0. (17.92)
For ν = 0 this differential equation can be stated as follows:
(kU
1
− ω)(f
− k
2
f) − kU
1
f =0. (17.93)
This equation (Rayleigh equation) is only of second order, and therefore
only two of the boundary conditions formulated in the preceding section can
be introduced into the solution. They are usually employed as follows:
y =0 ; f(0) = 0 and y →∞ ; f (→∞)=0. (17.94)
Neglecting the viscosity term in (17.92) leads to a drastic simplification
of the differential equation to be solved, because of the above-mentioned
reduction of the order. This was probably the reason why all initial studies
on the stability of flows were based on the Rayleigh equation (17.93). From
this results the following insight:
All laminar velocity profiles which show an inflection point, i.e. for which at
one location of the velocity profile d
2
U
1
/dy
2
= 0 holds, are unstable.
With this criterion, we have a necessary (Rayleigh) and a sufficient (Tollmien)
condition for the occurrence of flow instabilities. This fact alone makes it
clear that the curvature of velocity profiles has an important influence on the
stability of a flow.
Intuitively one would assume that the inclusion of a viscosity term in
(17.92), i.e. applying the Orr–Sommerfeld equation rather than the Rayleigh
equation, leads to an attenuation of introduced disturbances. This, how-
ever, cannot be confirmed. It rather turns out that the solution of the
Orr–Sommerfeld equation always has to be employed to obtain the approxi-
mately correct disturbance behavior of a flow in its initial phase. The insights
gained from such solutions can be plotted in so-called instability diagrams

17.5 Transitional Boundary-Layer Flows 521
Fig. 17.15 Instability diagram for boundary layers with and without viscosity term
in the Orr–Sommerfeld equation
as indicated in Fig. 17.15 for a flat plate boundary layer. This figure shows
that only a relatively narrow range of wavelengths and frequencies of distur-
bances have to be classified as “dangerous” for the stability of the boundary
layer. There always exists, for each investigated disturbance, a lower limit
for each Reynolds number of the boundary layer and an upper limit. Out-
side the so-called critical Re range that is characteristic of each disturbance,
boundary-layer flows prove to be stable.
When carrying out numerical computations, it results for C = ω/k that
C
R
U
∞
=0.39,kδ
1
=0.36 and
ω
R
δ
1
U
∞
=0.15.
It is interesting that the smallest wavelength of the disturbances which can
act in an unstable way on boundary layers is fairly long:
λ
min
=
2π
0.36
δ
1
=17.5δ
1
=6δ.
For smaller wavelengths of disturbances, boundary layers prove to be stable.
As the critical Reynolds number for the laminar-to-turbulent transition,
numerical computations yield
Re
crit
= 520
a value which is lower than the corresponding experimentally obtained value:
(Re
crit
)
exp
≈ 950.
The difference is probably due to the fact that the numerically determined
value Re
crit
= 520, ascertained from stability considerations, represents the
“point of neutral instability,” whereas the experimentally determined value
probably represents the “point of the laminar-to-turbulent transition that
occurs abruptly.” The two are, as can easily be understood, not necessarily
identical.
522 17 Unstable Flows
References
17.1. van Dyke, M.: “An Album of Fluid Motion”, Parabolic Press, Stanford, CA
(1982)
17.2. Currie, I.G.: “Fundamental Mechanics of Fluids”, McGraw-Hill, New York
(1974)
17.3. Oertel Jr., H.: “Prandtl-F¨uhrer durch die Str
´
’omungslehre”, Vieweg,
Braunschweig/Wiesbaden (2001)
17.4. Potter, M.C., Foss, J.F.: “Fluid Mechanics”, Wiley, New York (1975)
17.5. Schlichting, H.: “Boundary Layer Theory”, McGraw-Hill, New York (1979)
17.6. Sherman, F.S.: “Viscous Flow”, McGraw-Hill, Singapore (1990)
17.7. Taylor, G.: Stability of a Viscous Liquid Contained Between Two Rotating
Cylinders, Proc. R. Soc. A, 223, 289 (1923); Proc. Int. Congr. Appl. Mech.,
Delft, 1924; Z. Angew. Math. Mech., 5, 250 (1925)
