Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

Chapter 18

Turbulent Flows

18.1 General Considerations

In Chap. 17, we pointed out that special ﬂow properties exist to justify the

classiﬁcation of ﬂuid motions into laminar, transitional and turbulent ﬂows.

As laminar were designated all ﬂows which proved stable towards distur-

bances introduced from outside, resulting in ﬂows with a high degree of order

and in which diﬀusion phenomena are characterized only by molecular diﬀu-

sion. Laminar ﬂows can be dependent on time, as the Karman vortex street

shows, which is depicted in Fig. 18.1. As long as the ﬂow shows the high de-

gree of order which is characteristic of it, it is laminar. This means that the

viscosity of the ﬂuid is able, in stable laminar ﬂows, to attenuate suﬃciently

ﬂuctuations of the ﬂow properties that would otherwise disturb the orderli-

ness of the ﬂow. Perturbation attenuations of this kind usually occur at low

Reynolds numbers of all ﬂows.

When considering ﬂows at high Reynolds numbers, one ﬁnds that ﬂow

phenomena such as the Karman vortex street, visually perceivable thanks

to ﬂow visualization techniques, lose their “regularity,” i.e. stochastic ﬂuc-

tuations of all ﬂow properties are observed, as indicated in Fig. 18.2. These

ﬂuctuations occur superimposed on the mean ﬂow characteristics.

The ﬂuid motions, known to be of high regularity for laminar ﬂows, do not

exist any longer as orderly in turbulent ﬂows, i.e. in ﬂows of high Reynolds

numbers. At high Reynolds numbers, a ﬂow state exists which stands out for

its strong irregularity, in connection with an extremely high diﬀusivity which

can exceed the molecular-dependent transport processes by several orders of

magnitude. Connected with that is an increased intermixing of the ﬂuid and

an increased transport rate of the momentum, and also increased heat and

mass transport. All these characteristics led to the introduction of the term

“turbulence” for the state of ﬂows with this strongly irregular ﬂow behavior,

in order to give a clear expression of the diﬀering character compared with

laminar ﬂows. These diﬀerences have to be considered also when treating

523

524 18 Turbulent Flows

Fig. 18.1 The Karman vortex street, at low Reynolds numbers a time-varying

laminar ﬂow

Fig. 18.2 The Karman vortex street (at high Reynolds numbers) in a turbulent ﬂow

turbulent ﬂows theoretically, i.e. turbulent ﬂows require a speciﬁc treatment

which diﬀers from that of laminar ﬂows.

On introducing into a turbulent ﬂow ﬁeld a velocity sensor which is capable

of measuring the local instantaneous velocity, such a measurement results in

a velocity dependence on time, as indicated in Fig. 18.3. At a point in space,

the signal is characterized by strong ﬂuctuations of the ﬂow velocity in time,

which can be stated as deviations u



,t)fromameanvalueU

), the

latter being a constant with respect to time. Here, the time mean value

)isdeﬁnedasfollows:

) = lim

T →∞

,t)dt, (18.1)

where

,t) indicates the instantaneous value of the velocity (see Fig. 18.3)

and T is the integration time over which the indicated time-averaging takes

place.

Thus,

,t) can be taken as a quantity which allows one to consider

the local ﬂow velocity, varying over time, as the sum of a quantity that is

constant with respect to time and a quantity that is ﬂuctuating in time. This

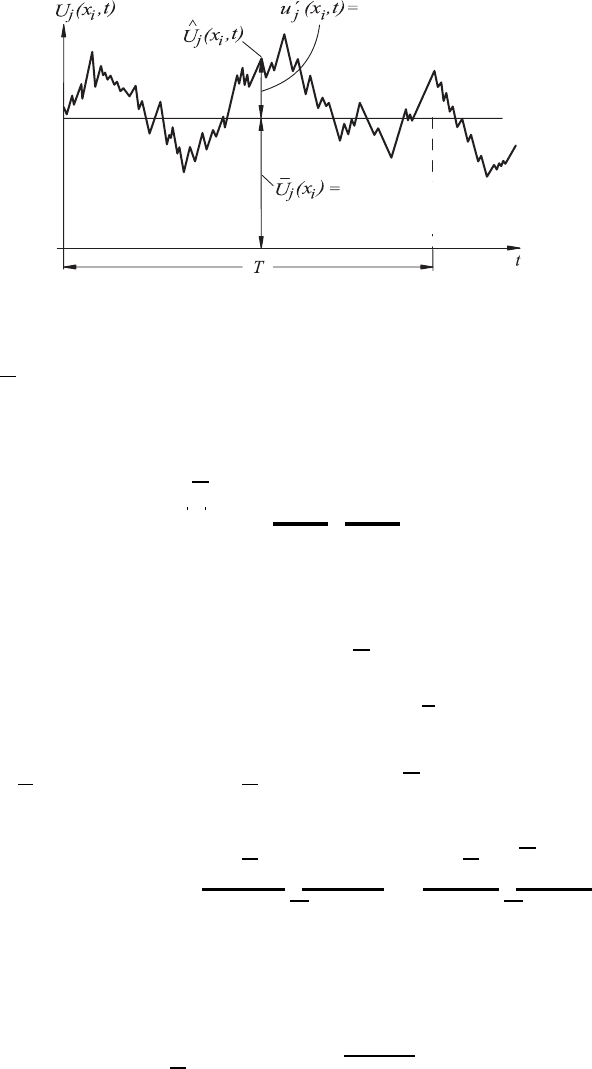
18.1 General Considerations 525

Turbulent fluctuation

of the velocity

component of

Time averaged

velocity component of

Fig. 18.3 Time velocity path at a point x

within a turbulent ﬂow ﬁeld

decomposition of the instantaneous velocity

,t) into a time-averaged

part

) and a ﬂuctuating part u



,t) has advantages, as will be shown

later. It was introduced by Reynolds to treat turbulent ﬂows.

The above deﬁnition of the mean velocity states, for T →∞, an equality

in area:



rectangular

area

= lim

T →∞

(t)dt

  

integral over

time-dependent signal

. (18.2)

When considering this deﬁnition of the time mean value of the velocity,

then for the quantity u



,t), designated as turbulent velocity ﬂuctuation,

the following equation holds:



,t)=

,t) − U

). (18.3)

When applying to this relationship the operator lim

T →∞

()dt, the following

can be carried out:

lim

T →∞



,t)dt = lim

T →∞



,t) − U

)



= lim

T →∞

,t)dt

  

− lim

T →∞

)dt

  

(18.4)

It can be concluded that the two integrals shown on the right-hand side of

(18.4) are equal and their diﬀerence yields 0, i.e. the following holds for the

time average of turbulent velocity ﬂuctuations:

lim

T →∞



,t)dt = u



,t)=0, (18.5)

526 18 Turbulent Flows

where the overbar on u



,t) represents a simpliﬁed way of writing the

carried out time averaging. On designating the turbulent velocity ﬂuctuations

with u



,t) (or simplifying this to u



), then the following can be said:

• The time average of the turbulent velocity ﬂuctuations u



is equal to zero

per deﬁnition. Hence, there is a way to present turbulence in local, time-

varying quantities, in a form such that the turbulent ﬂuctuations of all

ﬂow quantities, that are introduced into the considerations, show a time

mean value that is zero.

For the ﬂuctuating velocity quantity u



, moments of higher order can also be

deﬁned:



= lim

T →∞



dt, (18.6)

which in general show values diﬀerent from zero. Especially for the rms value

of the turbulent velocity ﬂuctuations, the following holds:





lim

T →∞



dt. (18.7)

This can be employed for the deﬁnition of the turbulence intensity:

Tu=



tot



+ u



tot

. (18.8)

This quantity represents a measure of the intensity of the turbulent ﬂuctua-

tions of the velocity components with respect to the local mean value

tot

As shown in (18.8), it is often usual to take as a relative value the mean

value of the total velocity vector, i.e.

tot



.TheTu-value is often

only around a few percent for some ﬂows and, because of this, one speaks of

a turbulent ﬂow of low intensity. When the value is around 10% and more,

the ﬂow is deﬁned as highly turbulent. Highly turbulent ﬂows occur mostly

in industrial ﬂow systems. It is the task of ﬂuid mechanics to develop and

bring to application measurement techniques and numerical solution methods

which allow investigations of turbulent ﬂows with low and high turbulence

intensities. In practice, it is often suﬃcient to only have information on time

mean values of turbulent quantities of an investigated ﬂow ﬁeld.

The introductory explanations above indicate clearly that turbulent ﬂow

ﬁelds show a complex behavior, providing strong property variations in space

and time, so that detailed considerations are only worth the eﬀort if spe-

cial insights into the physics of turbulence are needed. For practical ﬂow

considerations, it is suﬃcient to treat turbulent ﬂow processes by means of

their statistical mean properties, i.e. to describe the most important char-

acteristics of turbulent ﬂows by statistical mean values. In this chapter, the

18.2 Statistical Description of Turbulent Flows 527

most important methods of statistical ﬂow considerations are summarized

and explained brieﬂy, in order to employ them subsequently in the treatment

of turbulent ﬂows. More details are found in refs. [18.4] to [18.9].

18.2 Statistical Description of Turbulent Flows

As emphasized in Sect. 18.1, turbulent velocity ﬁelds are characterized by

strong irregularities of all their properties, e.g. strong changes of their ve-

locity and pressure in space and time. To register them, at all times and

at all locations, is not only a task which is diﬃcult to solve and that

exceeds our present measuring and representation capacities of ﬂuid me-

chanical processes, but moreover constitutes a task whose solution is not

worth striving for. The solution would result in such a large amount of

information that it could not be possible to process them further, or to

exploit them, in order to gain new insights into ﬂuid mechanical pro-

cesses. The large amount of information which turbulent ﬂows possess due

to their time and space behavior, therefore does not serve to deepen our

ﬂuid mechanical knowledge, nor does it help to improve ﬂuid-ﬂow equip-

ment and/or its installation. As ﬂuid-ﬂow information is only useful to the

extent to which it can be mentally grasped and exploited further, it is nec-

essary to reduce appropriately the large amount of information available

in turbulent ﬂow ﬁelds. In today’s turbulent ﬂow research, this is done by

mainly limiting investigations to two types of questions relating to turbulent

ﬂows:

• How do the local turbulent ﬂuctuations of the velocity components and

pressure vary around the corresponding mean values? What correlations

exist between the ﬂuctuating quantities, and what physical signiﬁcance do

these correlations have?

• How are neighboring turbulent ﬂuctuations of the velocity components

and pressure correlated with one another, and what physical signiﬁcance

do these correlations have?

To be able to give answers to these questions, one uses in turbulence re-

search methods of statistics and nearly all the terminology related to it.

The distribution of the local turbulent ﬂow ﬂuctuations and the turbulent

pressure ﬂuctuations are recorded by the probability density distribution

℘(u



)or℘(p



), or by their Fourier transforms, the so-called characteris-

tic function ϕ(k). In order to describe the existing correlation between

neighboring points in terms of space and/or time, one uses appropriate

correlation functions or their Fourier transforms. To describe the locally

occurring ﬂuctuations in time, the auto-correlation function of the ﬂuctu-

ations is used and its Fourier transforms, or their corresponding energy

spectrum. All these quantities (probability density distribution, character-

istic function, auto-correlation function, energy spectrum, etc.) result from

528 18 Turbulent Flows

the instantaneous values of the velocity components and pressure describ-

ing the turbulent ﬂow ﬁeld, by applying mathematical operators which are

explained this chapter in a somewhat summarizing way. It is very impor-

tant for the further comprehension of the description of the characteristics

of turbulent ﬂows to understand the employment of these operators and to

realize their physical signiﬁcance. Further details are provided in refs. [18.1],

[18.3].

18.3 Basics of Statistical Considerations

of Turbulent Flows

18.3.1 Fundamental Rules of Time Averaging

For the treatment of turbulent ﬂows, a method of consideration was intro-

duced by Reynolds (1895), where the instantaneous values of the velocity

components, pressure, density, temperature, etc., are replaced by mean values

(which are deﬁned as constant in terms of time) to which the corresponding

time-varying, turbulent, ﬂuctuating quantities, deviating from the mean val-

ues, are additively superimposed. Consequently, the instantaneous values can

be written as follows:

Velocity components

,t)=U

)+u



,t), (18.9)

Pressure

P (x

,t)=P (x

)+p



,t), (18.10)

Temperature

T (x

,t)=T (x

)+t



,t), (18.11)

Density ˆρ(x

,t)=ρ(x

)+ρ



,t). (18.12)

The above quantities with overbars on them are the time-averaged values

and the quantities with a “hat,”

∧

, are the corresponding instantaneous

values. The values with primes,



, represent the turbulent ﬂuctuations.

When applying the time-averaging operator:

lim

T →∞

(···)dt (18.13)

to the instantaneous values of the above quantities, one obtains the time mean

values, and this makes clear that the averaging in time over the turbulent

ﬂuctuations of the quantities has the value 0. This means that the following

holds:

lim

T →∞



,t)dt = 0 and lim

T →∞



,t)dt = 0 (18.14)

18.3 Statistical Considerations 529

and further for the temperature ﬂuctuations t



and the density ﬂuctuations



lim

T →∞



,t)dt = 0 and lim

T →∞



,t)dt =0. (18.15)

Generally, we can therefore write:

lim

T →∞



,t)dt =0, (18.16)

where α



,t) stands for any randomly varying turbulent ﬂow property.

When applying time averaging to derivatives of the quantity ˆα =

a + α



the following can be shown to be valid:

∂ ˆα

∂x

= lim

T →∞

∂ ˆα

∂x

dt =

∂

∂x

⎡

⎣

lim

T →∞

(α + α



)dt

⎤

⎦

∂

∂x

. (18.17)

Furthermore, the following fundamental rules of time averaging can be stated:

(ˆα +

β)=¯α +

β, (18.18)

¯αα



=0 and ˆαα



= α



, (18.19)

¯α

β =¯α

β and ˆα

β =¯α

β + α



. (18.20)

With the help and the consequent application of the integration rules, stated

above for the time averaging procedure, further relationships can be derived

for combinations of the functions ˆα(t)and

β(t).

When applying to the product of the instantaneous functions ˆα(t),

β(t)

and ˆγ(t) the time averaging rules above, the following relationship results:

ˆα

βˆγ = (¯α + α



)(

β + β



)(¯γ + γ



)=(¯α

β + α



β + β



¯α + α



)(¯γ + γ



)

¯α

β¯γ + α



β¯γ + β



¯α¯γ + α



¯γ +¯α

βγ



+ α



βγ



+ β



¯αγ



+ α



=¯α

β¯γ + α



¯γ + α



β +



¯α + α



(18.21)

In this way, triple products of the mean values of ˆα,

β and ˆγ are obtained,

products of correlations of two quantities multiplied by the mean value of the

third quantity, and triple correlations of the turbulent ﬂuctuation quantities



, β



and γ



result.

The above time averaging rules are employed in the subsequent sections,

in order to derive equations for the mean values from the basic equations

530 18 Turbulent Flows

of ﬂuid mechanics. The latter are usually formulated for the instantaneous

values of the velocity, pressure, etc. In all the derivations in this chap-

ter, the ﬂuid properties are assumed to be constant, and especially ρ =

constant. The resultant equations derived in this way indicate the mean

volume change by the time-averaged continuity equation, the mean mo-

mentum transport by the time-averaged momentum equation and the mean

energy transport by the time-averaged energy equation. On subtracting these

equations from the equations for the corresponding instantaneous values, one

obtains transport equations for the ﬂuctuating quantities. The latter can be

employed for gaining information on these properties of turbulent ﬂows.

18.3.2 Fundamental Rules for Probability Density

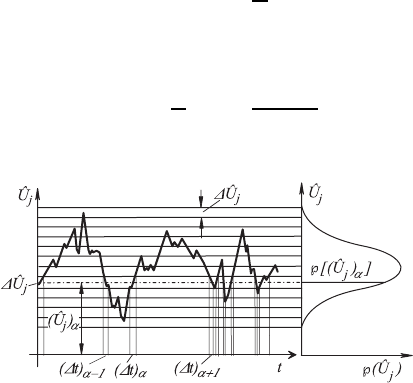
For the introduction of the probability density function for the velocity

components

,t), the velocity axis in Fig. 18.4 is subdivided into equal

sections ∆

. The velocity distribution is plotted along the time axis, as

obtained at a ﬁxed x

measuring location in a turbulent ﬂow ﬁeld. For the

considerations carried out here, the velocity distribution over time can be

assumed to be given for each velocity component

(j =1, 2, 3). The hori-

zontal lines of the subdivision of the

axis now lead for each velocity interval

∆U

to a corresponding period of time (∆t)

= f[(

)

,∆U

]. This time in-

terval indicates how long the velocity trace stays in the corresponding time

interval. On summarizing all time intervals which are assigned to the same

velocity interval, the probability density function can be deﬁned as follows:

lim

∆

→0

℘







∆



= lim

T →∞

lim

N→∞



α=1

(∆t)

(18.22)

or rewritten:

℘







= lim

T →∞

lim

∆U

→0

(∆

)



α=1

(∆t)

. (18.23)

Fig. 18.4 Time path of the velocity and resultant probability density distribution

18.3 Statistical Considerations 531

The probability density distribution deﬁned in this way contains all the

required information that indicates in which amplitude range the velocity

moves in time at a given measuring location. It indicates, moreover, with

which probability the amplitude of the ﬂuctuating velocity components oc-

cur in the course of time. The resultant function is also shown in Fig. 18.4,

as a distribution function, which is plotted along the

axis. It describes, in

a time-averaged way, the amplitude of the velocity ﬂuctuations occurring at a

point in the turbulent ﬂow. The computation of time-averaged values can thus

also take place through the corresponding probability density distribution,

as the entire amplitude distribution for the turbulent velocity ﬂuctuations is

recorded in it.

For the mean value of the velocity, discussed in Sect. 18.1:

j,(x

)

= lim

T →∞

,t)dt (18.24)

the time-related increment dt can be written as

= ℘





. (18.25)

For the integral

+∞

−∞

℘





, one can therefore derive from (18.25):

+∞

−∞

℘





dt =1, (18.26)

i.e. the “area” below the probability density distribution has the value 1.

The computation of the mean value of the local instantaneous ﬂow velocity

,t), as given in (18.25), can be computed with the help of the probability

density function. This means that two possibilities exist for computing the

mean value, computation in the time domain or in the probability density

domain:

) = lim

T →∞

)(t)dt =

+∞

−∞

℘(

)

. (18.27)

Here, ℘(

) is to be considered as being given for a ﬁxed location x

,t) represents the instantaneous value of the jth velocity component.

It is usual in turbulence research to state the probability density distribu-

tion only for the turbulent ﬂuctuations, i.e. ℘(u



). This probability density

distribution arises from the distribution shown in Fig. 18.4 by a parallel dis-

placement of the ordinate axis by the amount of the mean velocity

.With

this parallel displacement the form of the probability density function does

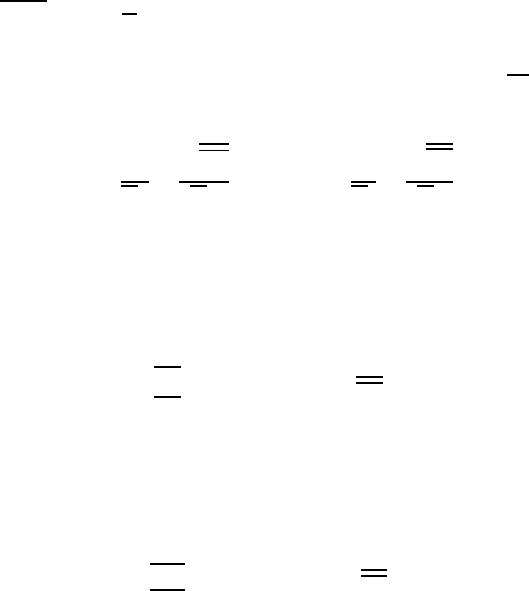
532 18 Turbulent Flows

not change and it thus provides, in this new coordinate system, the amplitude

values of the turbulent ﬂuctuations only.

Analogous to the time mean value computation with (18.27), one can

also compute the following moments of the velocity ﬂuctuations. On the one

hand, computations can be carried out in the time domain of the velocity and,

on the other hand, in the probability density domain. Both methods yield

the time-averaged properties for the nth moment of the turbulent velocity

ﬂuctuations:



)

= lim

T →∞



(t)

dt =

+∞

−∞

℘(u



)(u



)



. (18.28)

Of special importance in turbulence research is the second moment

,which

is employed for the deﬁnition of the turbulence intensity, α =1, 2, 3:





or Tu





. (18.29)

Moreover, the “standardized third moment” of the turbulent velocity ﬂuctu-

ations is included in several considerations, which allows statements about

the “skewness” of the probability density distribution of the turbulent veloc-

ity ﬂuctuations. Here, the “skewness” is deﬁned in the following way as the

standardized value of the turbulent velocity ﬂuctuations:



with σ









. (18.30)

For the corresponding standardized fourth moment, one often ﬁnds the term

“ﬂatness” used in the literature. It represents another important property of

the probability density distribution of turbulent velocity ﬂuctuations. As for

the skewness above, the ﬂatness is again deﬁned as a standardized quantity

(kurtosis):

4

with σ









. (18.31)

The above moments of higher order for the velocity ﬂuctuations are de-

ﬁned as central moments of the probability density distributions of the

corresponding components of the turbulent velocity ﬁeld.

In turbulence research, it is often necessary to deﬁne correlations between

the diﬀerent velocity ﬂuctuations. They are computed from the diﬀerent time-

varying velocity ﬂuctuations u



and u



as time integration over the products

of the ﬂuctuations, according to the equation below. They can also be com-

puted, in a corresponding way, using the two-dimensional probability density

distributions.